不确定性信息下的内河失控船应急决策方法

吴兵，严新平，汪洋，魏晓阳

（武汉理工大学智能交通系统研究中心国家水运安全工程技术研究中心，湖北武汉430063）

不确定性信息下的内河失控船应急决策方法

吴兵，严新平，汪洋，魏晓阳

（武汉理工大学智能交通系统研究中心国家水运安全工程技术研究中心，湖北武汉430063）

为解决内河失控船应急处置过程中的不确定性信息问题，本文提出了基于证据推理和逼近理想解排序法（TOPSIS）的应急处置决策方法。建立了内河失控船应急决策三层决策框架，确定了内河失控船应急决策的目标层、决策准则层和影响因素层。建立了目标层的评价等级，并对影响因素层的定性和定量数据进行评价，应用规则推理的方法将影响因素层评价转换到相应的目标层评价等级。应用证据推理的方法整合了各影响因素评价结果，获取了不同部门不同方案下的决策准则矩阵。应用TOPSIS的方法实现了决策方案的选择。选取了一起典型内河失控船险情对提出的模型进行了验证，研究结果表明：该方法可以很好地处理失控船应急处置决策过程中存在的不确定性信息，且能够采用精确值而非区间值进行最终决策。

失控船；证据推理；逼近理想解排序法；应急群决策；不确定性信息

水上交通险情发生后，如果不能及时有效地进行应急处置，容易诱发二次事故［1-3］。失控船作为一种典型的水上险情，其安全问题一直备受关注［4-6］。根据江苏海事局2007-2012年统计数据显示，该辖区每年约有100艘/次该类险情的发生。根据该历史统计数据，失控船的应急处置方法主要有四种:在拖轮协助下继续作业（A1），冲滩或者在航道外侧锚泊（A2），锚泊于就近的锚地（A3），应急锚泊于航道（A4）。另外和普通船舶类似，失控船的航行安全也会受到自然环境（决策准则一），交通环境（决策准则二）和安全管理（包括应急救助资源，决策准则三）［7-9］的影响，同时根据Generic ship的理论［10］，还受到船舶安全状态（决策准则四）的制约，这四个因素就构成了失控船应急决策的准则。从实际统计数据来看，这四个决策准则是细分为风、流、能见度［8，11-12］等影响因素的。因此失控船的应急处置实际上是一个具有三层结构框架的决策问题。另一方面，由于应急过程中涉及到失控船、过往船舶和海事部门等三个部门的协同处置，这个决策过程还是一个多部门协同的群决策问题。

对于具有多层结构特征的决策问题，模糊推理的方法应用非常广泛［12-14］。但需要注意的是，该方法一般用于处理具有完整信息的数据。而失控船应急过程中由于时间压力或事物本身复杂性等原因，对于某些变量难以精确量化，往往采用具有一定置信度的多个语言变量进行描述，且多个置信度之和小于或等于1，而未分配的置信度（小于1时）即为决策过程中的不确定性信息［15］，模糊推理难以对该类不确定性信息进行考虑。证据推理由于可以很好地考虑该类不确定性信息，其应用也非常广泛［9，16-17］。需要指出的是，由于有不确定性信息的存在，采用该方法时最终决策只能使用一个包含最大效用值、最小效用值和平均效用值的方法。对于某些决策方案，由于其最小效用值和最大效用值的区间值和另一方案的区间值重叠，只能采用平均效用值进行比较，严格来讲，对于两个具有相互交叉的区间值的比较，其大小关系应具有一定的概率［18］，因此该方法直接应用于失控船应急决策问题仍有一定的缺陷。

基于以上情况，本文拟考虑采用如下方法建立失控船的应急处置决策模型。首先建立失控船应急决策的三层结构决策框架，其次利用规则转换的方法建立各个影响因素的评价等级和目标层评价等级的关系，根据考虑两类不确定性信息的证据融合方法，获得各个决策准则的评价值（区间效用值），建立多准则决策矩阵。在此基础上，不再对决策准则信息和多部门信息进行融合，而是分别建立多部门的具有区间效用值的多准则决策矩阵，应用TOPSIS［18］对该决策问题进行排序。

1　不确定性信息下失控船应急决策问题描述

失控船应急决策是一个典型的具有三层结构框架的决策问题，一般由目标层、决策准则层和影响因素层（该层可进一步扩充为多层）组成，如图1所示。为保持本模型的通用性，假定多个决策准则表示为A=｛ai，i=1，2，…，I｝，其相应的权重为w=｛wi，i=1，2，…，I｝。第i个决策准则对应的影响因素层为，其相应的权重为，权重采用归一化权重，即

令目标层的决策变量有N个不同的评价等级，用来描述决策者对于该变量的偏爱程度，其中n值越大，该评价等级越受偏爱，各评价等级可表示为

对于第k个决策方案（k=1，2，…，K），其第i个决策准则层的第j个影响因素的评价结果可表示为

图1　失控船应急处置三层决策框架Fig.1 Three-level decision framework for NUC ship handling

在确定了各个影响因素的评价结果后，利用DS合成规则对其进行融合，获取不同决策方案下的决策准则值，这就构成了以不同决策方案不同决策准则值为元素的某一部门的决策矩阵。另外根据各个部门dm=dc，c=1，2…，C

｛｝的不同决策信息，可以获取各个部门的决策矩阵。

2　不确定性信息下失控船应急决策模型

2.1基于证据推理的决策矩阵获取

2.1.1定性和定量影响因素评价

在进行各影响因素信息融合之前，需要将不同种类的数据（定性和定量数据、不同单位数据等）统一到式（1）所示的格式中。根据杨剑波［16］的方法，可以利用规则或效用值的方法进行转换，考虑到本文的数据特点以及研究的侧重点，此处仅介绍基于规则的转换方法。该方法根据数据特点可以分为定性和定量两类:

1）对于定量数据，其评价结果可表示为

式中:hn，j是指第j个影响因素的可能数值，Nj表示存在的数值的个数，则是对应的置信度，且满足

2）对于定性数据，首先需要建立影响因素的评价等级，第j个影响因素的评价等级可表示为

其次，建立其不同评价等级的评价结果，表示为

式中:Hn，j表示为第j个影响因素的评价等级，则是其对应的置信度，且满足和。Nj代表评价等级的个数，当Nj与N相同时，式（3）与式（1）等同。

在对定性和定量数据分别进行评价后，可通过文献［16］的方法实现由式（2）、（3）到式（1）的转换。考虑到该转换过程较为复杂，且IDS软件［16-17］可以自动实现该转换过程，本文对其转换过程不再详述。

2.1.2影响因素D-S证据融合

根据文献［17］的证据融合规则，按照各个影响因素的权重对置信度进行加权，表示为。并对未分配的不确定性信息分为由权重造成的不确定性和由初始不确定性信息造成的不确定性且令为第i个准则所包含的影响因素的子集，根据如下公式即可实现各个影响因素的证据融合:

获得了两类不确定性信息后，需要将由权重造成的不确定性信息按照比例重新分配，其重新分配按照下式进行:

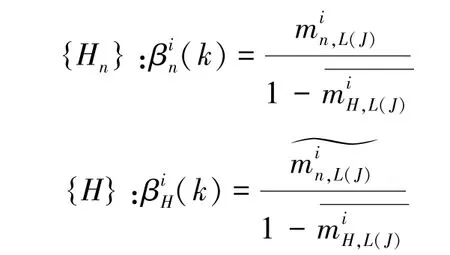
由此可获得各个决策准则的评价结果，为

式中:Hn表示第k个决策方案下，第i个决策准则的评价等级，需要指出的是，该评价等级已经转换为目标层的评价等级，两者是相同的。为其置信度，为多个具有不确定性信息的影响因素合成之后仍存在的不确定性信息:

2.1.3建立多准则决策矩阵

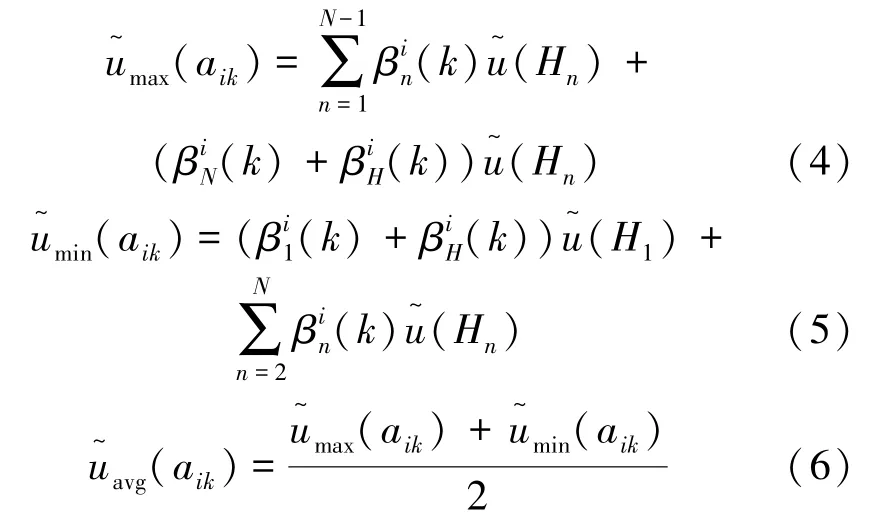
因此可得到各决策方案下的决策准则的决策矩阵如下

式中:xik为一个区间值，即，简化表示为

考虑到决策过程中存在多个部门协同的情况，式（7）可进一步表示为

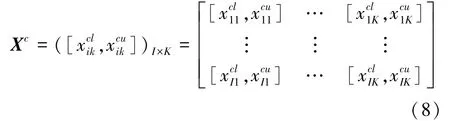
式中:c=1，2…，C为协同部门的编号。

2.2基于TOPSIS的多部门多准则决策

2.2.1获取决策矩阵

在获取了各决策准则的决策矩阵后，考虑到各决策准则的重要程度不同，需要对各决策准则赋予一定的权重。需要注意地是本方法既可以对各决策准则赋予一个区间权重，也可以赋予一个确定权重，考虑到应急决策过程中难以较精确地描述各决策准则的权重，因此采用区间权重赋值。令决策准则权重为，其中根据区间值相乘的基本定理［18］，可获得加权后的决策准则矩阵:

除了各决策准则的权重外，还需要考虑到各决策部门的权重，和决策准则权重类似，该权重既可以是区间值也可以是确定值，仍采用区间值，获得加权后决策矩阵:

2.2.2选取正负理想点决策矩阵

根据TOPSIS［18］方法，需要选取各个决策部门的最大值和最小值做为决策的正负理想点，在进行选取之前，需要对式（9）的元素进行变换，转换为，获取决策部门的正理想点矩阵θ+和负理想点矩阵θ-如下:

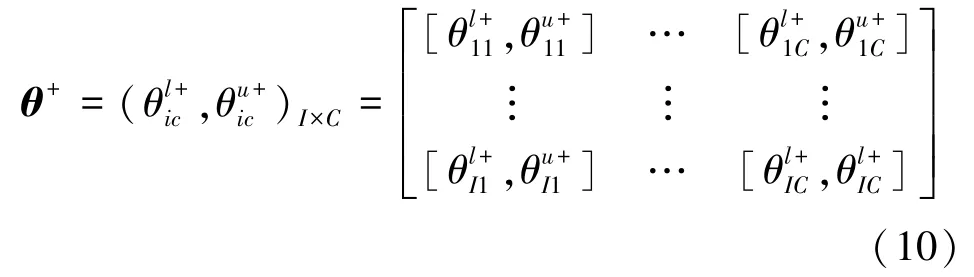
式中:

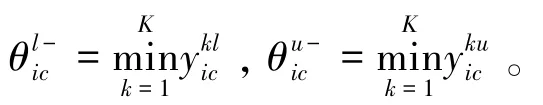
2.2.3决策方案最终排序

根据文献［18］提供的方法，可以获取决策准则值和正负理想矩阵与决策矩阵Zk～之间的距离:

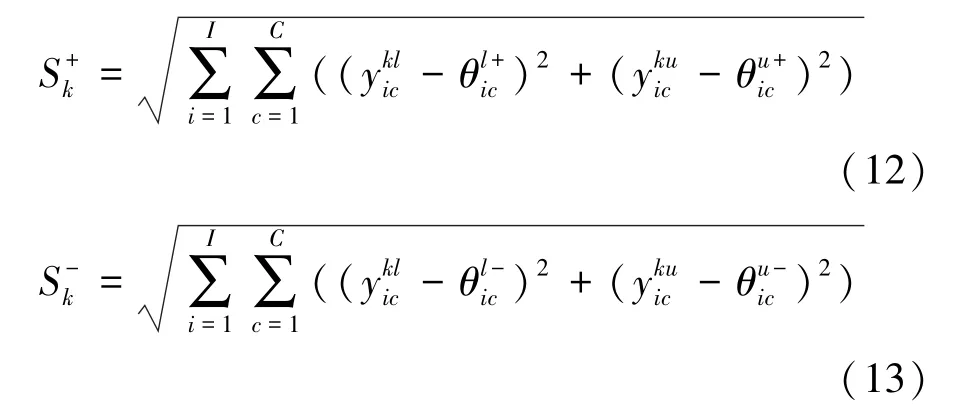
从而获取各决策方案的相对值，其中相对值越大，代表该方案越优越:

3　失控船应急决策实证研究

3.1失控船应急决策情景

本案例改自2011年发生于长江下游86#左右通航浮的一起舵机失控险情，失控船船长145 m，险情距离泰州长江大桥约2.3 km，距离20#停泊区约5 km。另外由于三个部门信息来源的渠道不同，其对于某些影响因素的数据会存在一定的差异，如流速、交通流量等。同时对于部分影响因素还存在不确定性信息，如风级影响因素，海事部门距离现场相对较远，其风级数据为3～4级风，3级和4级风可能性相当，置信度均为0.4，另外还存在一定的阵风可能，其置信度为0.1；而失控船位于险情现场，其风级为4级，置信度为0.9，也存在置信度为0.1的阵风。又如失效预计恢复时间，失控船舶对自身船舶状况和船员素质最为熟悉，能够预估该信息，而其他两个部门则缺少这方面的信息。各部门信息如表1所示，需要指出的是，各影响因素的顺序与表2相同，本表中采用编号代替。

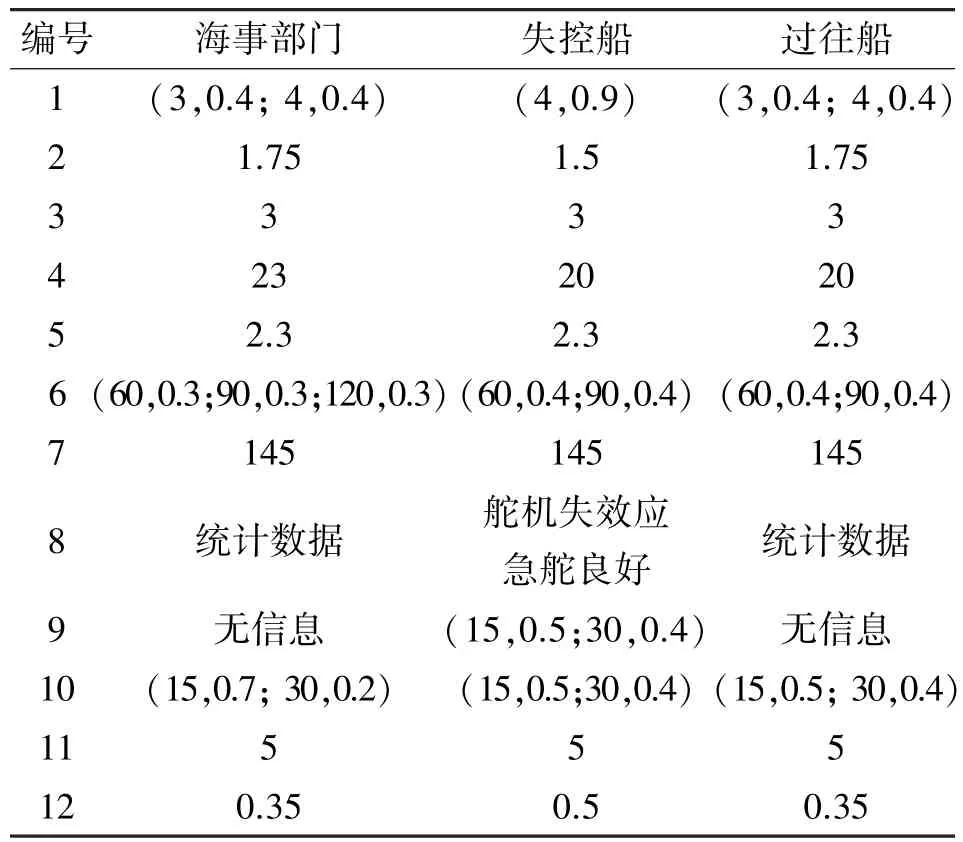
表1　不同部门的险情信息数据Table 1 Detailed information for different departments

3.2影响因素决策等级转换

首先建立目标层的评价等级为五级，表示为

其次对影响因素层的定性和定量数据进行评价。对于定量数据，根据规则推理的方法，通过设定五个与目标层评价等级对应的可能值，以A1方案下的风级为例，可以设定风级的评价等级如表2所示。当风级为8级时，A1方案对应worst；风级为 7级时，A1方案对应 poor，以此类推。根据此方法，可以建立不同方案下的定量数据的评价等级。

而对于定性数据（即失控模式），本案例考虑建立四等级的评价等级，各等级代表含义分别为:代表全船失电；

再次，根据表2建立的评价方法，可以利用文献［16］的方法将相对应的具体数值转换到目标层的评价等级中，具体可利用 IDS［16-17］软件实现，如海事部门A1方案风级，其数值为（3，0. 4；4，0.4）。

对定性数据（即失效模式），在进行评价前需建立转换矩阵，其与目标层评价等级对应关系矩阵Pni:

再根据IDS软件［16-17］，即可实现定性数据评价结果与目标层评价等级的转换。

3.3获取多部门决策矩阵

通过假定各影响因素在各个决策准则中的权重相同，将IDS［16-17］计算获得的各评价结果进行证据融合后，可获取不同部门不同决策方案下的决策准则的评价信息，采取与文献［16］相同的评价等级效用值，分别如下

进一步根据式（4）、（5），可以获得各部门不同方案下的决策矩阵，如表3所示。

3.4最终决策方案

分别对各决策准则和决策部门进行赋权，考虑到各决策准则和各部门在决策过程中的重要程度，其权重分别为

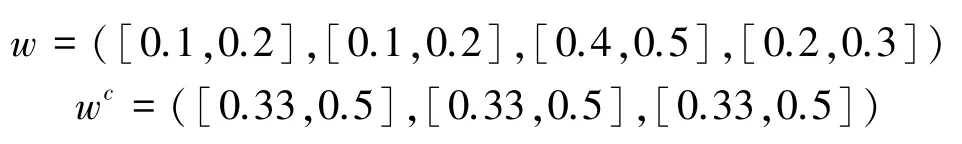
根据式（7）、（8），可获得加权后的决策矩阵如表4所示。

根据式（10）、（11），可获得正负理想点矩阵如表5所示。

根据式（12）～（14），可分别求得 S+、S-和RC，如表6所示。

从结果可以看出，A3方案即为最优方案，这与实际应急处置情况一致，即锚泊于20#停泊区。实际上，本文还对其他失控类型（主机失效、全船失电）的失控案例进行了验证，结果表明该方法均是可行且有效的，考虑到篇幅因素，本文不对其他案例进行进一步分析。

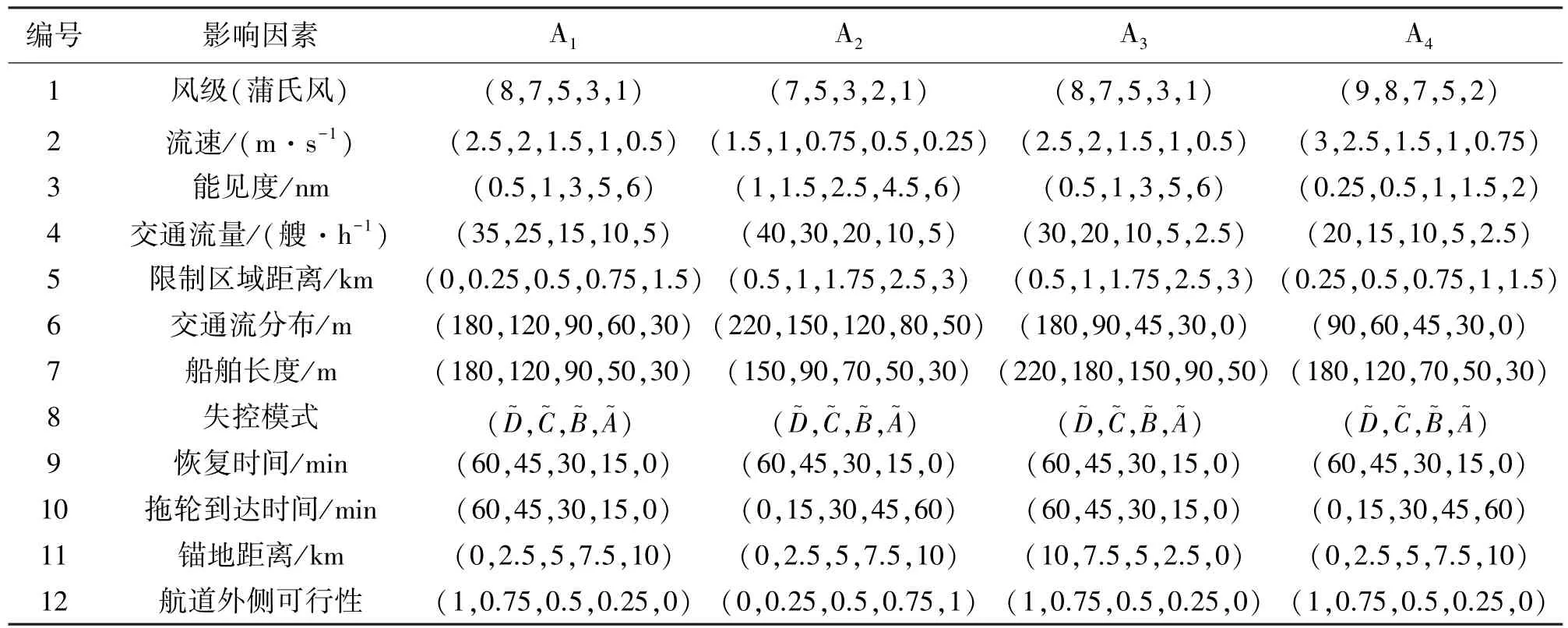
表2　定性和定量数据评价方法Table 2 Evaluation method for qualitative and quantitative data

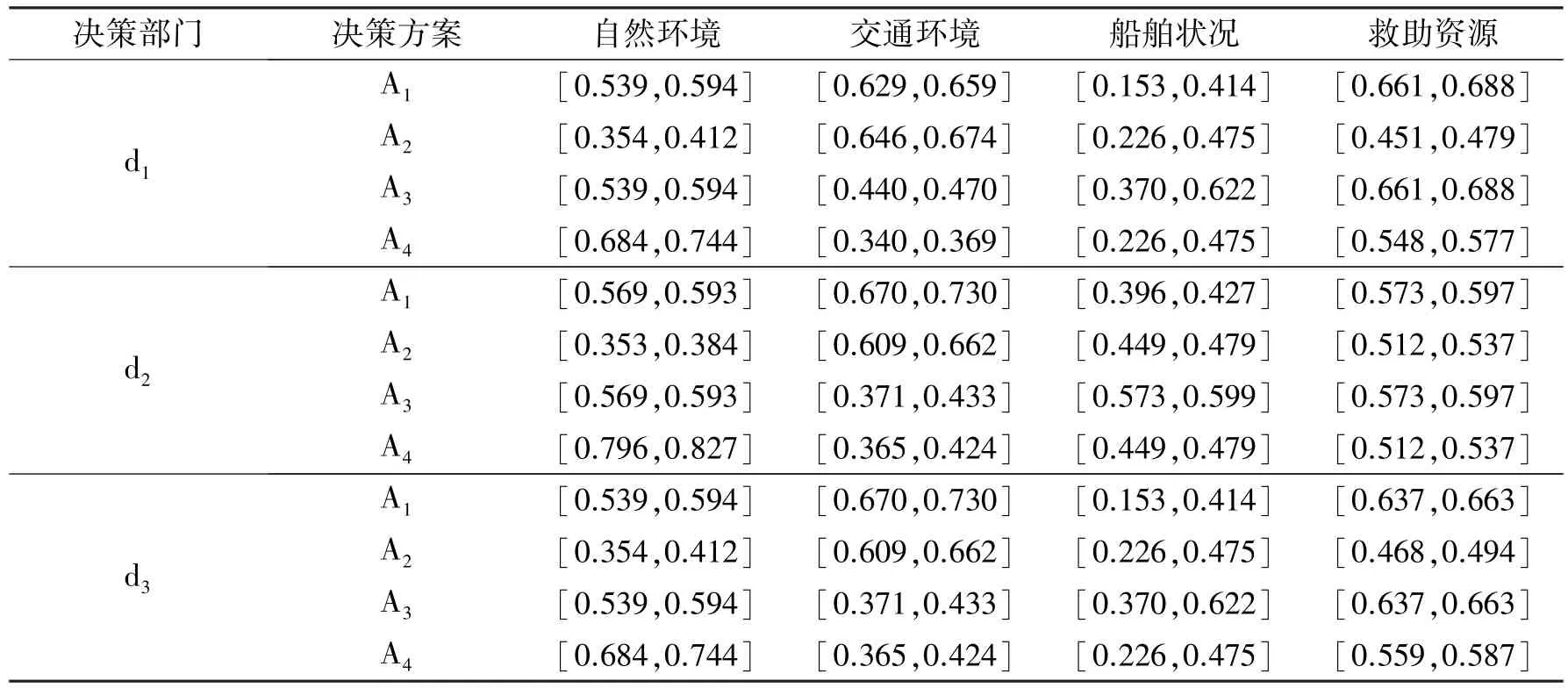
表3　各部门不同方案下的决策矩阵Table 3 Decision matrix of different attributes for different departments

表4　加权后各部门不同方案下的决策矩阵Table 4 Weighted decision matrix of different attributes for different departments

表5　正理想点和负理想点矩阵Table 5 Matrix for positive ideal point and negative ideal point

表6　失控船应急处置方案比较结果Table 6 Comparison result of handling alternatives for NUC ship

4　结论

本文提出的基于证据推理和TOPSIS的应急决策方法可以很好地实现内河失控船的应急处置，首先利用证据推理对存在不确定性信息的各影响因素进行融合，可以获取不同决策方案下的决策准则值，再利用TOPSIS的方法可以获取最优应急方案的选取。主要结论如下:

1）提出的方法可以很好的解决内河失控船应急处置决策过程中存在的问题。一方面，可以充分考虑不确定性信息对决策的影响，另一方面，该方法可以很好地整合各个部门所获取的不对称的不完整信息，并能够选择合理的应急处置方案。

2）提出的方法相比较于仅采用证据理论方法进行决策具有两个优势。一方面，可以避免仅使用证据推理方法时，需采用平均效用值来评价各个决策方案的情形；另一方面，对不同部门和不同决策准则赋予权重时既可以和证据推理一样采用精确值，还可以采用区间值，增加了该方法的可应用性和灵活性。

［1］ULUSCU Ö S，OZBAS B，ALTIOK T，et al.Risk analysis of the vessel traffic in the strait of Istanbul［J］.Risk analysis，2009，29（10）:1454-1472.

［2］ZHANG D，YAN X P，YANG Z L，et al.Incorporation of formal safety assessment and Bayesian network in navigational risk estimation of the Yangtze River［J］.Reliability engineering&system safety，2013，118:93-105.

［3］ZHANG Di，YAN Xinping，YANG Zaili，et al.An accident data-based approach for congestion risk assessment of inland waterways:a Yangtze River case［J］.Proceedings of the institution of mechanical engineers，part O:journal of risk and reliability，2014，228（2）:176-188.

［4］甘浪雄，喻晓，高国章.船舶失控应急的港珠澳大桥桥区水域尺度［J］.中国航海，2011，34（4）:76-80. GAN Langxiong，YU Xiao，GAO Guozhang.Range of bridge water area of Hong Kong-Zhuhai-Macao Bridge for out-of control ships in emergency［J］.Navigation of China，2011，34（4）:76-80.

［5］MAZAHERI A，MONTEWKA J，KUJALA P.Modeling the risk of ship grounding-a literature review from a risk management perspective［J］.WMU journal of maritime affairs，2014，13（2）:269-297.

［6］吴兵，严新平，汪洋，等.多部门协同的内河失控船应急处置决策方法［J］.交通运输系统工程与信息，2015，15 （5）:16-23. WU Bing，YAN Xinping，WANG Yang，et al.A modified decision-making method with multidivisional cooperation for disposal of NUC ships［J］.Journal of transportation systems engineering and information technology，2015，15（5）:16-23.

［7］吴兵，严新平，汪洋，等.基于桥梁通航风险的海巡艇配备研究［J］.中国航海，2013，36（4）:82-85，91. WU Bing，YAN Xinping，WANG Yang，et al.Maritime patrol resource configuration based on navigational risks in bridge area［J］.Navigation of China，2013，36（4）:82-85，91.

［8］WU Bing，WANG Yang，ZHANG Jinfen，et al.Effectiveness of maritime safety control in different navigation zones using a spatial sequential DEA model:Yangtze River case ［J］.Accident analysis&prevention，2015，81:232-242.

［9］张笛，张金奋，严新平.基于模糊规则库和证据推理的内河通航风险评价［J］.中国航海，2014，37（1）:71-75，98. ZHANG Di，ZHANG Jinfen，YAN Xinping.Navigational risk assessment for inland waterway transportation system based on fuzzy rule base and evidential reasoning［J］.Navigation of China，2014，37（1）:71-75，98.

［10］LOIS P，WANG J，WALL A，et al.Formal safety assessment of cruise ships［J］.Tourism management，2004，25 （1）:93-109.

［11］BALMAT J F，LAFONT F，MAIFRET R，et al.MAritime RISk Assessment（MARISA），a fuzzy approach to define an individual ship risk factor［J］.Ocean engineering，2009，36（15/16）:1278-1286.

［12］BALMAT J F，LAFONT F，MAIFRET R，et al.A decision-making system to maritime risk assessment［J］.Ocean engineering，2011，38（1）:171-176.

［13］LI Pengcheng，CHEN Guohua，DAI Licao，et al.Fuzzy logic-based approach for identifying the risk importance of human error［J］.Safety science，2010，48（7）:902-913.

［14］杜珺，王瑞红.基于三角模糊数的锂电池航空运输火灾事故树分析［J］.交通信息与安全，2014，32（3）:119-122，137. DU Jun，WANG Ruihong.Fire risk analysis of Lithium-ion Batteries in air transportation based on fault tree method and tri-fuzzy theory［J］.Journal of transport information and safety，2014，32（3）:119-122，127.

［15］YANG Z L，BONSALL S，WALL A，et al.A modified CREAM to human reliability quantification in marine engineering［J］.Ocean engineering，2013，58:293-303.

［16］YANG Jianbo.Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties［J］.European journal of operational research，2001，131（1）:31-61.

［17］YANG Jianbo，XU Dongling.On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty［J］.IEEE transactions on systems，man，and cybernetics-part A:systems and humans，2002，32（3）: 289-304.

［18］YUE Zhongliang.Group decision making with multi-attribute interval data［J］.Information fusion，2013，14（4）: 551-561.

本文引用格式：

吴兵，严新平，汪洋，等.不确定性信息下的内河失控船应急决策方法［J］.哈尔滨工程大学学报，2016，37（7）:908-914.

WU Bing，YAN Xinping，WANG Yang，et al.Emergency decision-making method for handling an out-of-control ship in inland water in case of uncertain information［J］.Journal of Harbin Engineering University，2016，37（7）:908-914.

Emergency decision-making method for handling an out-of-control ship in inland water in case of uncertain information

WU Bing，YAN Xinping，WANG Yang，WEI Xiaoyang
（Intelligent Transportation System Research Center，National Engineering Research Center for Water Transport Safety（WTSC），Wuhan University of Technology，Wuhan 430063，China）

To deal with uncertain information when handling an out-of-control ship in an inland waterway，we propose an emergency decision-making method based on evidential reasoning and the technique for order of preference by similarity to an ideal solution（TOPSIS）.We establish a three-level decision framework for handling an out-ofcontrol ship in an inland waterway，where the objective level，level for decision criterion，and level for influencing factors are defined.We establish the evaluation grades for the objective level，assess both qualitative and quantitative data with respect to the influencing factors，and use a rule-based technique to transform the influencing factors to the objective level.We introduce the evidential reasoning method to integrate the values of the influencing factors，from which we develop a decision criterion matrix of different alternatives with respect to different organizations.Next，we apply the TOPSIS method to select the best alternative.We use a typical inland waterway incident to verify the proposed method.The results demonstrate that this is a useful decision-making method for handling an out-of-control ship in an inland waterway，for which there is uncertain information.Moreover，this method can be used to make a final decision using a precise value rather than interval numbers.

out-of-control ship；evidential reasoning；technique for order of preference by similarity to ideal solution （TOPSIS）；emergency group decision-making；uncertain information

10.11990/jheu.201504070

U698.6

A

1006-7043（2016）07-908-07

2015-04-30.网络出版日期：2016-05-13.

国家科技支撑计划项目（2015BAG20B05）；高等学校博士学科点专项科研基金项目（20130143120014）.

吴兵（1986-），男，博士研究生；严新平（1959-），男，教授，博士生导师，博士.

严新平，E-mail:xpyan@whut.edu.cn.

网络出版地址：http：//www.cnki.net/kcms/detail/23.1390.u.20160513.1344.012.html