一种无人水面艇运动模型参数在线辨识方法

孙晓界， 石林龙,2， 范云生， 王国峰

(1.大连海事大学 信息科学技术学院， 辽宁 大连 116026； 2.上海船舶运输科学研究所， 上海 200135)

一种无人水面艇运动模型参数在线辨识方法

孙晓界1， 石林龙1,2， 范云生1， 王国峰1

(1.大连海事大学 信息科学技术学院， 辽宁 大连 116026； 2.上海船舶运输科学研究所， 上海 200135)

为实现无人水面艇运动模型参数的在线辨识，通过Z形操舵和定常回转的实船操纵性试验及其数据分析，利用递推最小二乘法对水面无人艇操纵运动响应型数学模型及舵机响应模型的参数进行辨识，设计并实现一种无人水面艇操纵运动模型参数在线辨识试验平台。基于所建立的数学模型和辨识的模型参数搭建无人水面艇操纵运动仿真系统。通过与实船试验数据进行对比分析，证明模型参数在线辨识试验平台设计的正确性和合理性。

船舶工程;无人水面艇；运动模型；递推最小二乘法；在线辨识

Abstract: The recursive-least-square based online identification of the motion model parameters of the Unmanned Surface Vehicle (USV) is introduced. The process identifies the maneuver response model and ruder gear response model following the maneuverability tests, such as zigzag tests and turning motion tests. The test facility for online identification of the USV motion model parameter is designed and built. The ship handling operation simulation system for the USV is developed based on the identification output. The comparison between the simulation outputs and sea trial results is presented, which shows that they agree with each other quite well, indicating that the model identification is dependable.

Keywords: ship engineering; USV； motion model； recursive least square； online identification

水面无人艇(Unmanned Surface Vehicle, USV)作为监测海洋环境、维护海洋权益的现代化海洋装备，具有广阔的应用前景，己成为国内外智能化海洋装备的研究热点。[1]面对复杂多变的海洋环境，获取水面无人艇操纵运动数学模型的参数既是设计运动控制器的基础，也是无人艇自主控制技术研究的核心内容之一。通常利用系统辨识的方法确定模型参数，主要包括最小二乘法[2-3]、扩展Kalman滤波法[4]、模型参考及模型参考自适应法[5-7]、极大似然估计法[8-9]、回归预报误差法[10]、岭回归分析法[11-12]、神经网络法[13-14]、频域谱分析法[15]、支持向量机法[16-17]和遗传算法[18]等。最小二乘法是其中最基本的方法，尤其是递推最小二乘法具有系统先验统计知识少、算法简单、计算量小、收敛性好等特点，可实现模型参数的在线辨识。[19-20]

以大连海事大学“蓝信”号水面无人艇为研究对象，建立响应型水面无人艇三自由度[21]平面运动线性化数学模型。通过分析Z形操舵响应和定常回转试验的实船数据，利用递推最小二乘法对水面无人艇响应型数学模型和操舵响应模型的参数进行辨识。基于所建立的数学模型和辨识的模型参数搭建无人水面艇操纵运动仿真系统;通过与实船试验数据进行对比分析，验证模型参数在线辨识试验平台设计的正确性和合理性。

1 USV数学模型及其参数辨识方法

1.1USV操纵运动数学模型

采用Nomoto模型[22]描述无人艇平面运动数学模型。

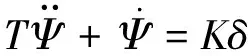
(1)

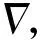
1.2舵机伺服系统模型

操舵过程的响应模型通常被视为一阶惯性环节，即

(2)

式(2)中：Tr为时间常数，无人艇一般取0.25 s；δr为命令舵角；|δ|≤35°为舵角实际所受的限制[23]。

然而,通过分析Z型试验过程中采集到的舵角响应数据可知，试验过程中实际舵角的变化不能简单地按式(2)处理,应针对实际操舵过程中的舵机响应特性，立足于试验过程采集到的实际无人艇数据，将舵机响应模型按二阶欠阻尼环节处理，即

(3)

式(3)中：ωn为自然频率;ζ为阻尼比;K为比例系数。

1.3模型参数辨识方法

参数递推估计是指对被辨识的系统,每取得一次新的测量数据就在前一次估计结果的基础上用其对前一次估计结果进行修正，从而递推出新的参数估计值。这样，随着新测得数据引入,逐次进行参数估计，直到估计值达到满意的精确度为止。

(4)

无人艇操纵性数学模型的系统辨识原理见图1。

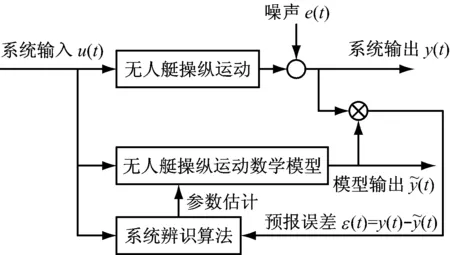
图1 无人艇操纵性模型的系统辨识原理

由于无人艇的Nomoto模型是线性系统，因此通过带有0阶保持器的Z变换方法得到其离散时间系统模型，通过实船回转试验得到输入舵角和输出航向数据，按照原理图的辨识方式和递推最小二乘法求得辨识后的Nomoto模型。同理，根据辨识试验中得到的舵机响应实时数据得到其二阶欠阻尼舵机响应模型辨识的参数。

2 在线辨识试验平台的设计

2.1试验平台总体设计

试验平台中，通过给无人艇的自动舵下达舵角指令，使其完成回转试验和Z型试验;通过VC++将试验中无人艇的航向、航速、舵角和指令舵角记录下来并上传到上位机中;在上位机中,通过MATLAB并根据当前记录的数据进行实时辨识，实时显示无人艇操纵运动数学模型和操舵响应模型的参数。

2.2试验平台界面设计

无人艇航行过程中遇到的操纵情况较多，无法全部进行实艇试验，只能找一些较为典型的操纵情况加以试验，由此得到若干个能表征无人艇操纵性能的参数进行分析和比较。这里以“蓝信”号无人艇为实船试验平台，利用VC++程序实时显示其运行状态，设计并进行实艇的回转试验和Z型试验。

进行实艇的回转试验是为了考察无人艇的回转性能，可由处理试验数据得到的回转性指数K来表征。无人艇回转试验软件截图见图2。

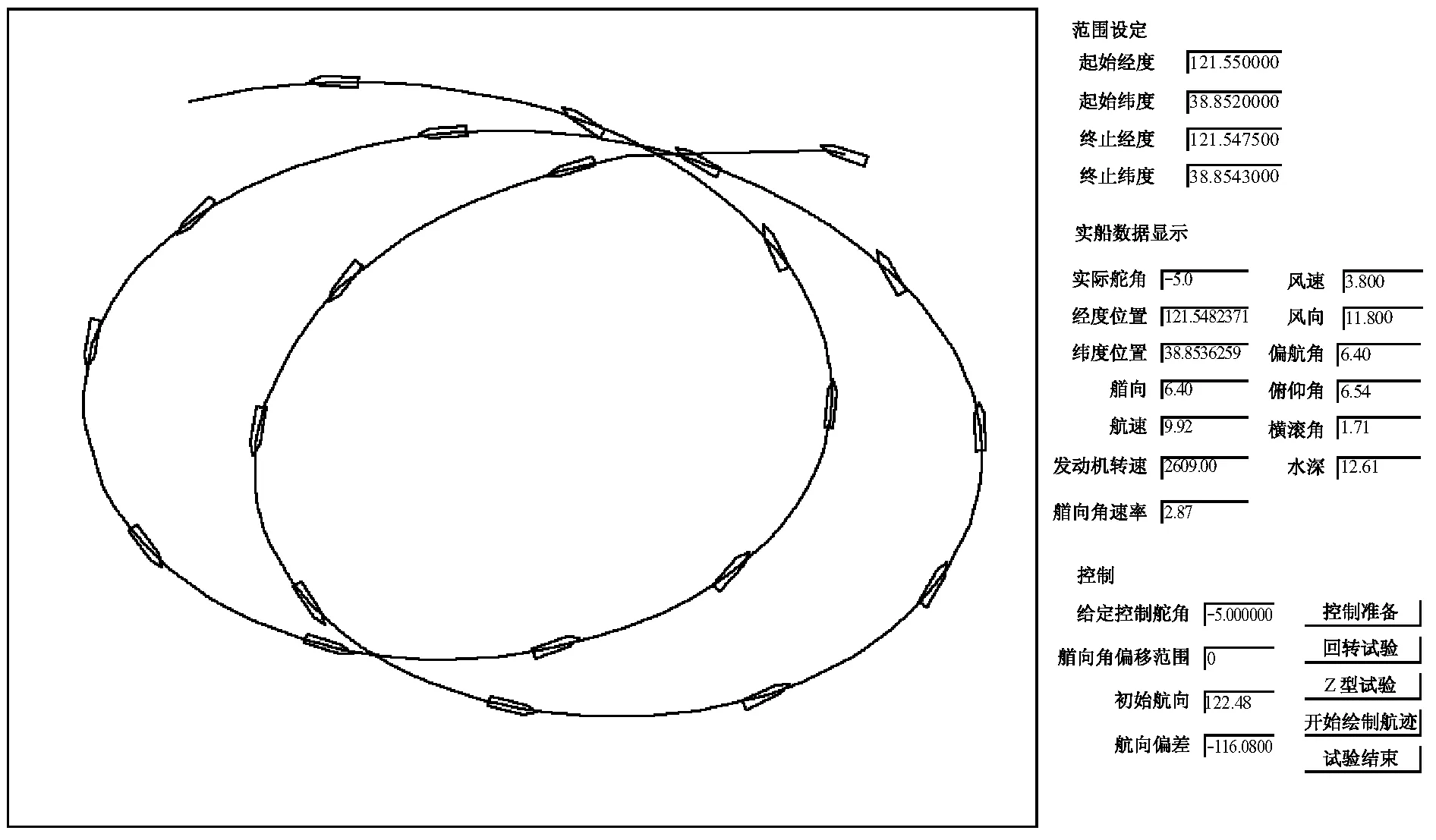
图2 无人艇回转试验软件截图

由船舶的实际操纵情况可知，类似回转试验长期保持一定舵角不变的情况并不多，因此进行实艇的Z型操纵试验是必要的。进行Z型操纵试验主要是为了考察艇体在中、小舵角下改变和保持航向的能力，并测定回转性指数K和应舵指数T。无人艇Z型操纵试验平台软件截图见图3。

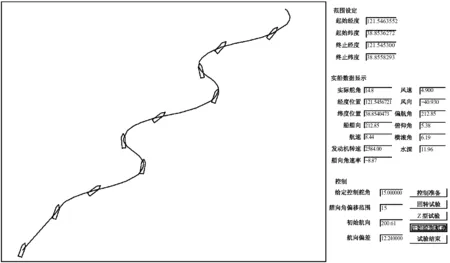
图3 无人艇Z型试验软件截图

2.3实船试验与数据获取

在一级海况下对无人艇进行回转试验。舵角稳定在5°左右，航速保持在10 kn左右，得到实船回转试验的采样点数据，采样时间为0.5 s。当所操舵角不大(10°以内)时，船舶回转性能可用线性响应模型来描述，且可忽略船舶纵向航速的变化，将其视为常数。此外，操舵速度也可不予考虑，认为是阶跃操舵。[25]由于需要实时记录的数据较多，这里只列出首圈采样点数据(见表1)。

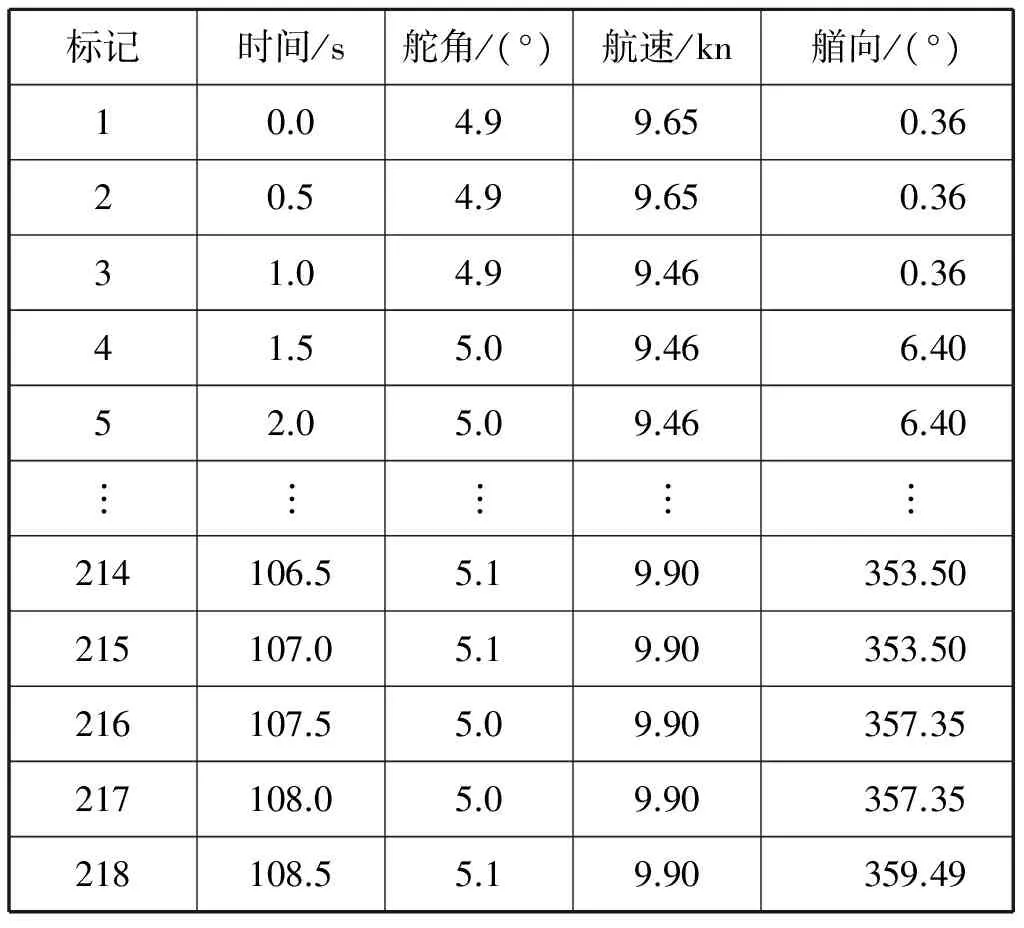
表1 一级海况下实船回转试验的首圈采样点数据

在同等海况条件下对无人艇进行15°/15°Z型操纵运动试验，无人艇航速保持在9 kn左右；待试验准备就绪并发出操舵指令后，即以最快操舵速度将控制舵角变为右15°;当艏向角达到右15°时，立即执行操舵指令,使控制舵角由右15°变为左15°;待艏向角改变达到左15°时，再立即执行操舵指令,使控制舵角由左15°变为右15°。按照以上流程，执行5次以上操舵指令即为一次完整的Z型试验。在整个试验过程中，允许控制舵角与实际达到的舵角存在一定误差，不必为改变实际舵角而调整控制舵角的值。由于需要实时记录的数据较多，这里只列出首次操舵指令采样点数据(见表2)。

表2一级海况下实船Z型试验的首次操舵指令采样点数据(初始艏向为235.04°)

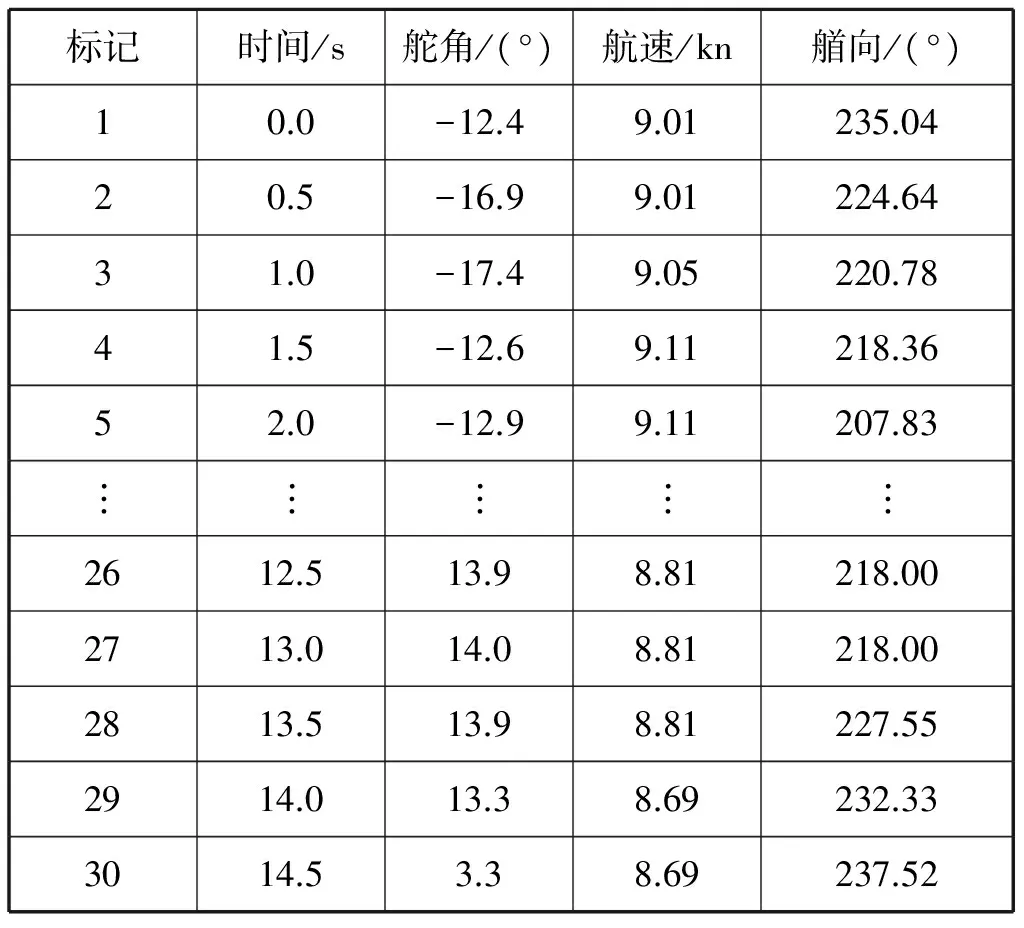
标记时间/s舵角/(°)航速/kn艏向/(°)10．0-12．49．01235．0420．5-16．99．01224．6431．0-17．49．05220．7841．5-12．69．11218．3652．0-12．99．11207．83︙︙︙︙︙2612．513．98．81218．002713．014．08．81218．002813．513．98．81227．552914．013．38．69232．333014．53．38．69237．52

3 在线辨识试验平台的数据分析

3.1模型参数的辨识结果

对于无人艇操纵性模型，在回转试验中通过实时辨识得到的回转性指数平均值为K=0.644，参数估计收敛曲线见图4；在Z型试验中通过辨识得到的回转性指数平均值为K=0.701，应舵性指数平均值为T=0.332，参数估计收敛曲线见图5。可见，由回转试验数据辨识得到的K值与Z型试验得到的K值基本吻合，试验数据具有很高的可信度。

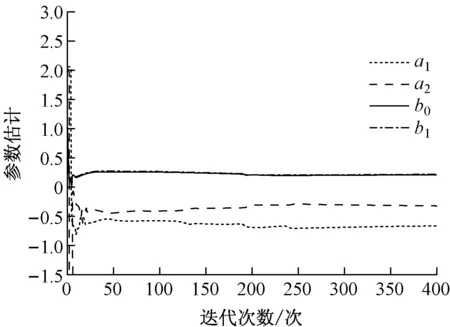
图4 回转试验参数估计收敛曲线

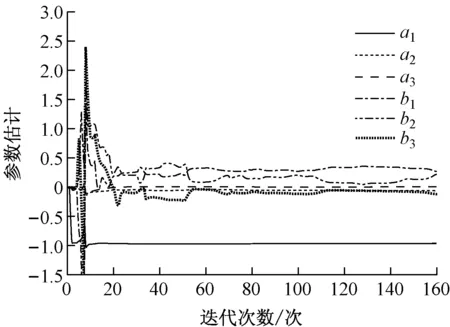
图5 Z型试验参数估计收敛曲线

对于操舵响应模型，只能通过Z型试验来辨识，通过实时辨识得到自然频率平均值为ωn=0.958，阻尼比平均值为ζ=0.811，放大系数K=0.923，参数估计收敛曲线见图6。

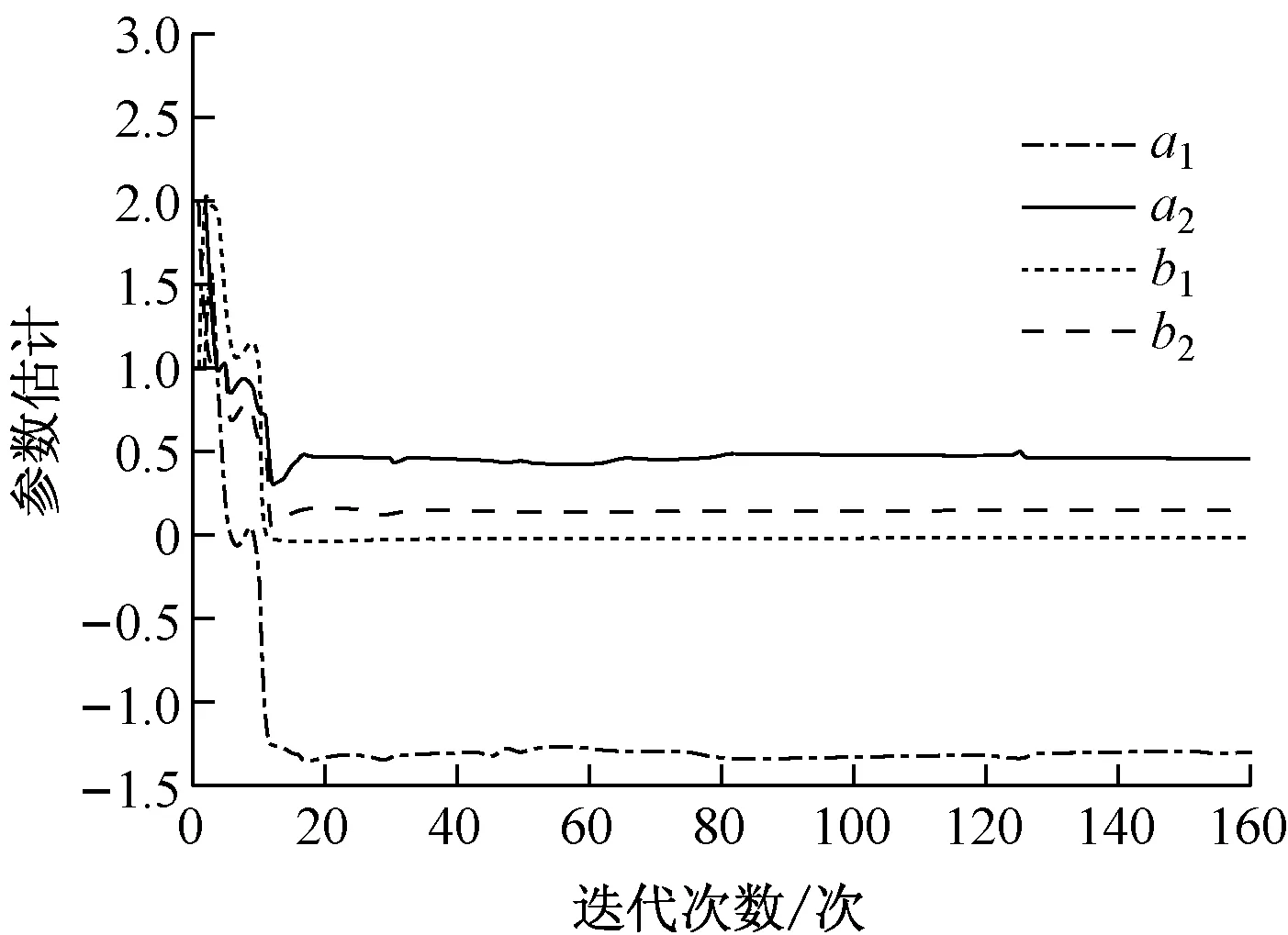
图6 响应舵模型参数估计收敛曲线

3.2辨识结果分析

对利用辨识得到的Nomoto无人艇数学模型进行回转仿真试验，在与实际数据中给出的舵角、航速相同的条件下，得到回转试验的仿真结果见图7。

图7 回转试验仿真结果

根据实船回转试验的采样点数据，可得到实船回转试验中记录下的无人艇的运动轨迹(见图8)。

通过试验得到无人艇的仿真稳定回转半径为85.762 1 m,实船稳定回转半径为84.971 6 m。通过比较可知，船舶模型在实际可信范围内。

对通过辨识得到的Nomoto无人艇数学模型及自然频率为ωn=0.958，阻尼比为ζ=0.811，放大系数为K=0.923的操舵响应模型进行Z型试验，在与实际数据中给出的舵角、航速相同的条件下，得到Z型试验的仿真结果见图9。

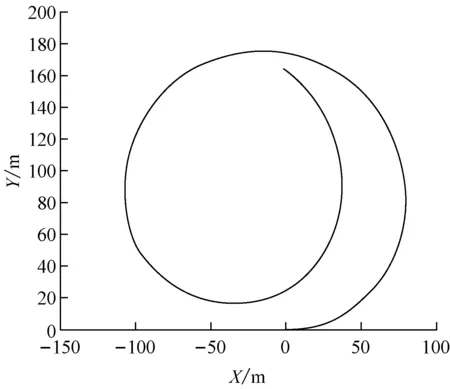
图8 实船回转试验结果

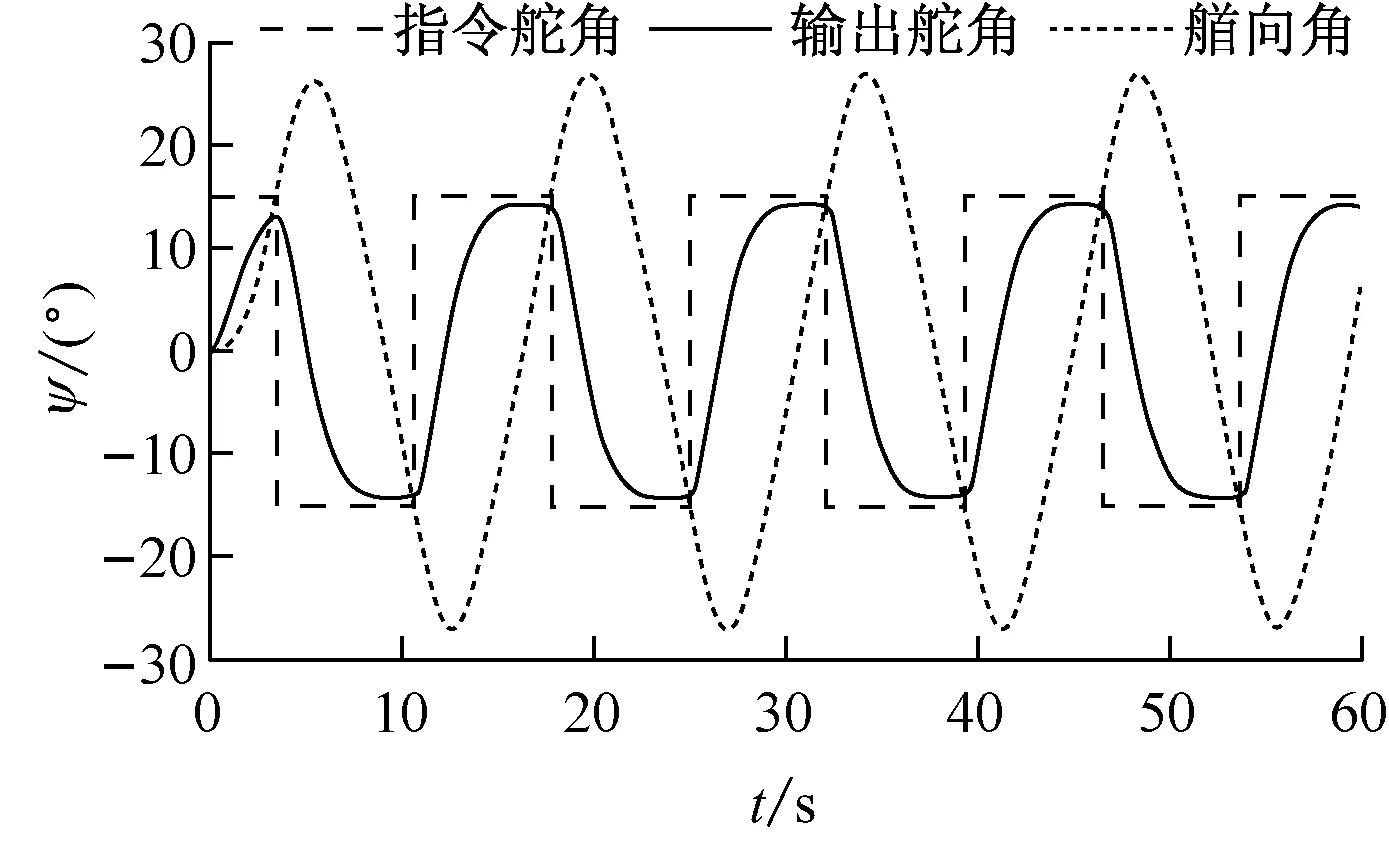
图9 Z型试验仿真结果(15°/15°)

根据实船Z型试验的采样点数据，可得到实船Z型试验中所记录下的无人艇的舵角和艏向角变化轨迹(见图10)。

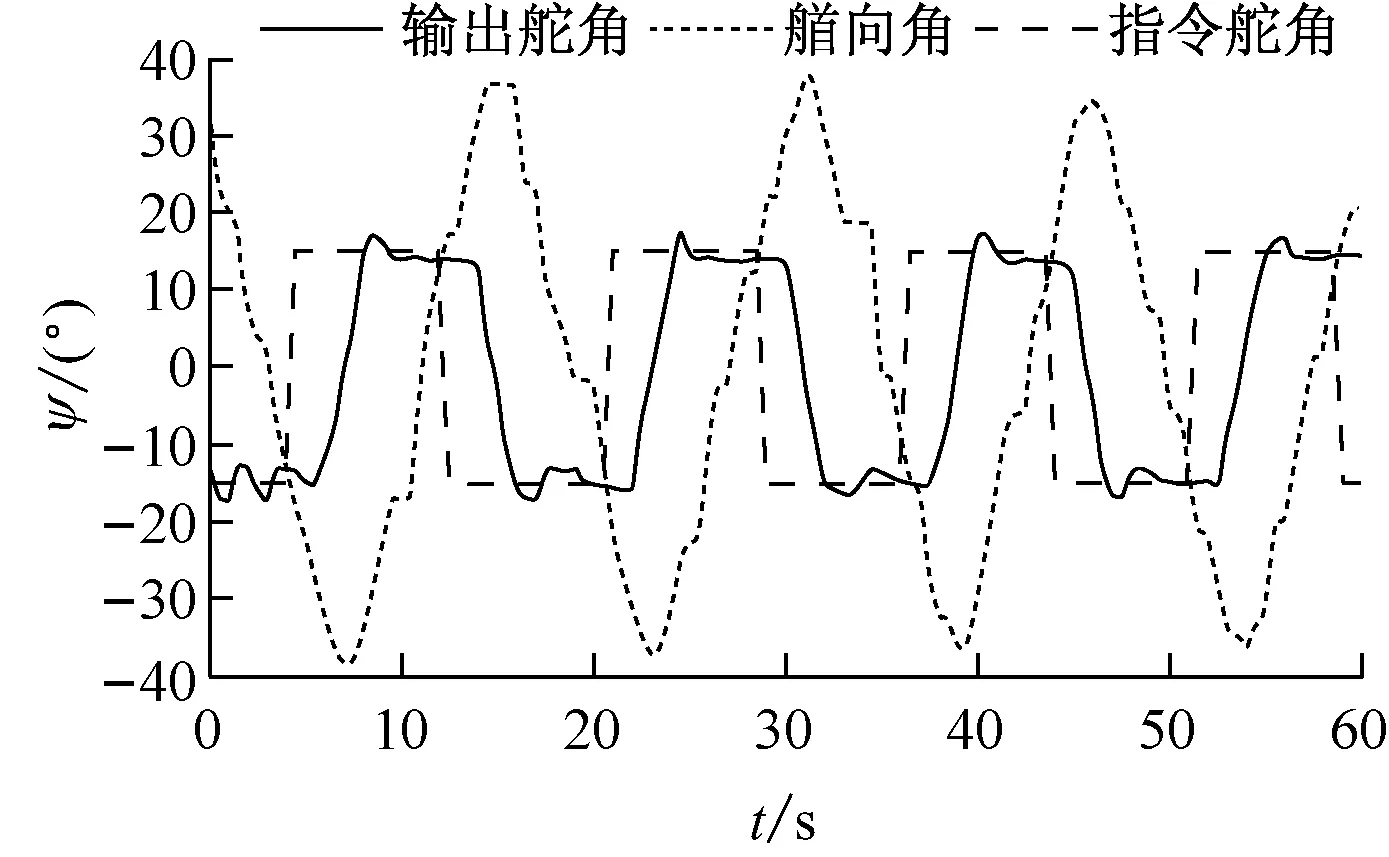
图10 实船Z型试验结果(15°/15°)

对比图9和图10可知，仿真试验的Z型应舵周期为14.356 s，而实际Z型试验的应舵周期为16.5 s。

为进一步验证模型的正确性，进行15°/10°的Z型操纵运动试验，无人艇航速仍保持在9 kn左右。可得到15°/10° Z型试验的仿真与实船试验结果,见图11和图12。

对比图11和图12可知,仿真试验所得Z型应舵周期为12.376 s，而实船Z型试验的应舵周期为14.0 s。可见，无人艇在实际海况下的应舵周期与辨识得到的模型通过仿真绘制得到的应舵周期较为接近。考虑到辨识得到的无人艇模型与理想模型必然存在一定差距，可认为通过实船试验数据辨识得到的无人艇操纵运动响应型模型能反映实船的真实性能，可以采用。

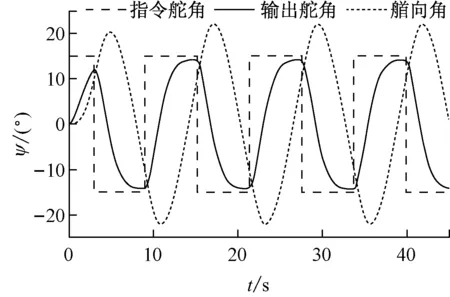
图11 Z型试验仿真结果(15°/10°)

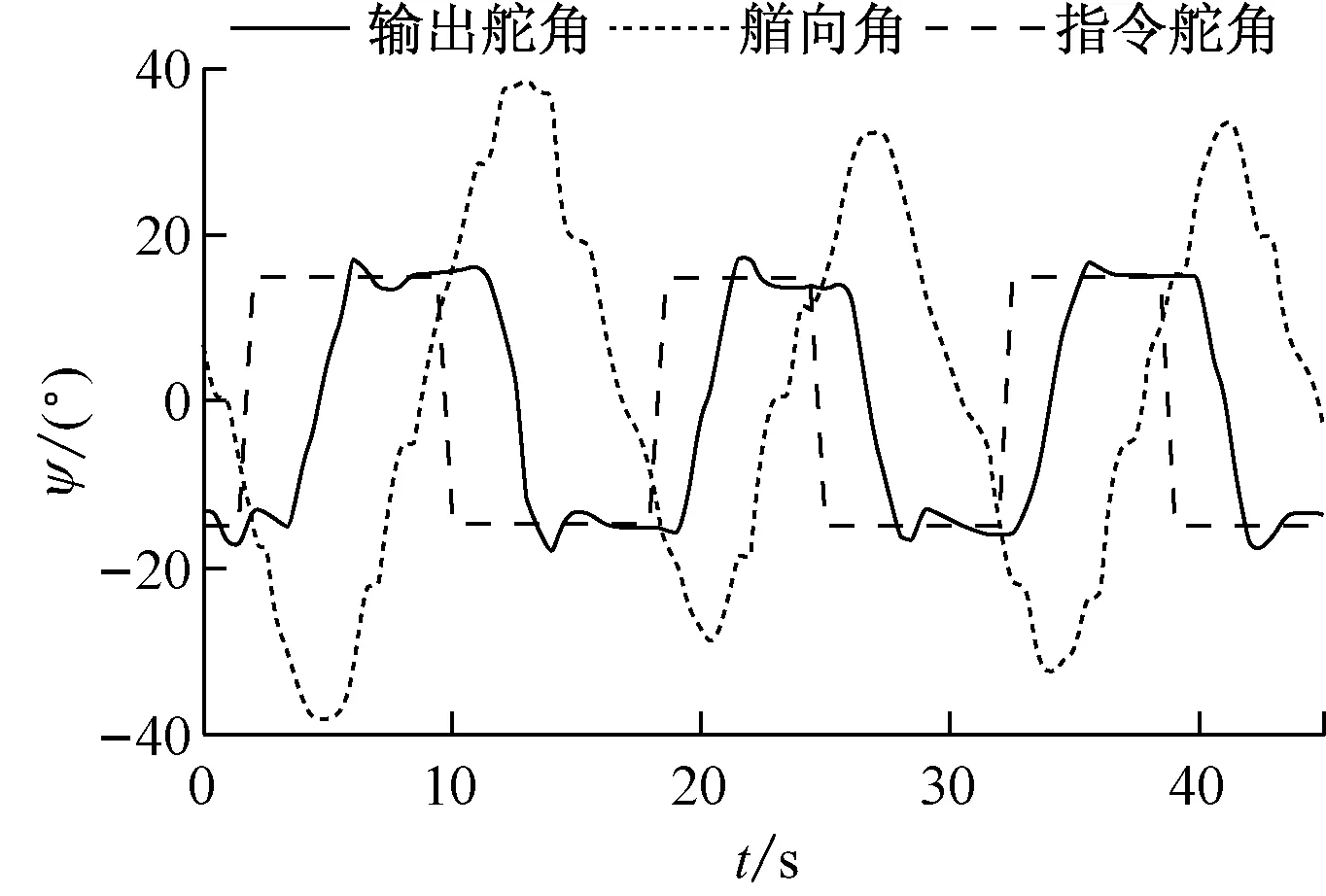
图12 实船Z型试验的结果(15°/10°)

4 结束语

以大连海事大学“蓝信”号水面无人艇为研究对象，在适宜海况条件下进行多组实船回转试验和Z型试验，得到能反映无人艇实船操纵运动性能的数据，并以此为基础进行分析研究。利用递推最小二乘法对水面无人艇操纵运动响应型数学模型的参数和舵机响应模型的参数进行辨识，设计并实现一种无人水面艇操纵运动模型参数在线辨识试验平台，辨识到“蓝信”号无人艇的操纵运动响应型模型的参数和舵机响应模型参数。基于所建立的数学模型和辨识的模型参数搭建无人水面艇操纵运动仿真系统。通过与实船试验数据进行对比分析，验证了“蓝信”号无人水面艇操纵运动模型参数在线辨识试验平台设计的正确性和合理性。

[1] VOLKER B. Unmanned Surface Vehicles-A Survey[D]. Copenhagen: Skibsteknisk Selskab, 2008.

[2] KOYAMA K. Analysis of Full-Scale Measurement of Manoeuvrability by Trial and Error Methods[R]. ShipBuilding Laboratory, University of Tech. Delft, 1971.

[3] 张洪东, 李宏, 郑勇. 基于递推最小二乘法的永磁同步电动机参数辨识[J]. 微特电机, 2011, 39(11):14-16.

[4] ABKOWITZ M A. Measurement of Hydrodynamic Characteristic from Ship Maneuvering Trials by System Identification[J]. Transactions of Society of Naval Architects and Marine Engineers, 1980(88):283-318.

[5] HAYES M N. Parameters Identification of Nonlinear Stochastic Systems Applied to Ocean Vehicle Dynamics[D]. Ph.D. Dissertation, M.I.T., 1971.

[6] VAN A J. Adaptive Steering of Ships-A Model Reference Approach[J]. Automatica, 1984, 20(1):3-14.

[7] 韦文祥, 刘国荣. 间接矢量控制中的转子电阻辨识方法研究[J]. 控制工程, 2014, 21(6):838-842.

[8] ÅSTRÖM K J, KLLSTRÖM C G. Identification of Ship Steering Dynamics[J]. Automatica, 1976(12):9-22.

[9] 安其昌, 张景旭, 孙敬伟. 基于极大似然估计的TMT三镜轴系装调[J]. 红外与激光工程, 2013, 42(11):3002-3007.

[10] ZHOU W W, BLANKE M. Identification of a Class of Nonlinear State-Space Models Using RPE Techniques[J]. IEEE Transaction on Automatic Control, 1989, 34(3):312-316.

[11] 罗伟林, 邹早建. 基于岭回归方法的船舶操纵运动建模[J]. 船海工程, 2009, 38(6):17-19.

[12] 温瑞英, 王红勇. 基于岭回归—BP神经网络的管制工作负荷预测方法[J]. 交通运输系统工程与信息, 2015, 15(1):123-129.

[13] MOREIRA L, GUEDES S C. Dynamic Model of Manoeuvrability Using Recursive Neural Networks[J]. Ocean Engineering, 2003, 30(13): 1669-1697.

[14] 谷鑫, 胡升, 史婷娜, 等. 基于神经网络的永磁同步电机多参数解耦在线辨识[J]. 电工技术学报, 2015, 30(6):114-121.

[15] BHATTACHARYYA S K, HADDARA M R. Parameter Identification for Nonlinear Ship Manoeuvring[J]. Journal of Ship Research, 2006, 50(3):197-207.

[16] LUO W l, ZOU Z J. Parametric Identification of Ship Manoeuvring Models by Using Support Vector Machines[J]. Journal of Ship Research, 2009, 53(1):19-30.

[17] 孙巧梅, 任光. 自适应逆控方法的无人艇航向控制[J]. 中国航海, 2012, 35(4):17-21.

[18] 王立军, 张显库. 响应型船舶运动模型的建模与遗传算法辨识[J]. 中国航海, 2013, 36(2):33-37.

[19] 李涌. 基于最小二乘法的汽轮机电液调节系统参数辨识[J]. 电力与能源, 2013, 34(1):27-29.

[20] 赵海森, 杜中兰, 刘晓芳, 等. 基于递推最小二乘法与模型参考自适应法的鼠笼式异步电机转子电阻在线辨识方法[J]. 中国电机工程学报, 2014，34(30):5386-5394.

[21] 郭晨, 汪洋, 孙富春, 等. 欠驱动水面船舶运动控制研究综述[J]. 控制与决策, 2009, 24(3):321-329.

[22] NOMOTO K, TAGUCHI T, HONDA K,etal. On the Steering Qualities of Ships[J]. Int. Shipbuilding Progress, 1957, 4(35):188-194.

[23] 杨盐生, 贾欣乐. 船舶运动数学模型:机理建模与辨识建模[M]. 大连：大连海事大学出版社, 1999：234-249.

[24] TURKER E, HARVEY A. Improving Active Magnetic Bearing System Performance Using Recursive Least Square Method[C]. TENCON, 2006.

[25] 刘洋, 米伟, 郭晨. 船舶航向模糊自整定操舵控制器的研究[J]. 中国航海, 2010, 33(1):11-15.

OnlineParameterIdentificationofUSVMotionModel

SUNXiaojie1,SHILinlong1,2,FANYunsheng1,WANGGuofeng1

(1. College of Information Science and Technology, Dalian Maritime University, Dalian 116026, China；2. Shanghai Ship & Shipping Research Institute, Shanghai 200135, China)

2015-11-21

国家自然科学基金(61374114); 辽宁省自然科学基金(2015020022); 中央高校基本科研业务费(3132015039)

孙晓界(1992—)，男，河南洛阳人，硕士生，从事智能系统、船舶运动建模的研究。E-mail:sunxiaojie92@163.com

范云生(1981—)，男，辽宁丹东人，讲师，博士，从事交通信息工程及控制，智能控制理论与应用，无人系统测控技术的研究。 E-mail:fan_yunsheng@163.com

1000-4653(2016)01-0039-05

U661.3;TP391.9

A