液压系统复合控制的建模和应用

张　强，　李向辉，　马　旻

（中国重型机械研究院股份公司， 陕西　西安　710032）



液压系统复合控制的建模和应用

张强，李向辉，马旻

（中国重型机械研究院股份公司， 陕西西安710032）

以一台大型拉伸矫直机的主液压系统为例，对各个主要元件模型的获得方法进行了详细分析，并给出了泵控缸的数学模型和阀控缸的数学模型以及复合控制时采用比例泵或伺服阀进行补偿的方框图。通过将实际数据代入上述数学模型的计算，为类似复合控制液压伺服系统的设计和调试提供理论依据。

复合控制泵控缸阀控缸

在伺服液压系统中，以变频电机+定量泵或伺服（比例）变量泵为控制元件的容积式控制（又称为泵控）和以伺服（比例）阀为控制元件的节流式控制（又称为阀控）是最主要的两种控制形式。相比较而言，容积式伺服液压系统具有效率高、流量大、调速范围宽、速度稳定性高的特点；节流式伺服液压系统则具有动态响应快、控制精度高等特点[1]。随着机械设备在大负载、高精度方面的发展，更大的负载必然要求更大的液压缸径和更高的工作压力，而随着系统快速性与控制精度的不断提高，单纯只靠泵控或阀控的工作方式已经不能满足机械设备对伺服液压系统的性能要求。如何将泵控和阀控结合在一起，利用两者构成的复合控制方式实现伺服液压系统对液压缸的高压、大流量、快速、高精度控制已经成为国内外液压行业的一大技术难题。本文以中国重型机械研究院为某厂设计的一台大型铝板拉伸矫直机的主拉伸液压系统为例，详细分析通过复合控制液压缸实现主拉伸液压系统高压、大流量、快速、高精度的方法。

1　比例泵控制液压缸数学模型的获取

该大型铝板拉伸矫直机的主拉伸液压系统以两个单出杆柱塞式液压缸作为主缸，每个主缸均以复合控制形式在两侧单独控制且在运动过程中保持位置同步[2]。铝板拉伸矫直机的主拉伸液压系统中泵控缸元件如图1所示。

图1　单侧比例泵控制主缸的原理框图

主拉伸液压系统中泵控缸部分是以比例泵控制单出杆柱塞式液压缸的。为使最终的系统模型尽可能真实反映系统的实际性能，同时兼顾系统模型的复杂程度，根据各元件对系统性能影响所占的比重，对系统性能影响较大的元件采用较高级别的传递函数表达，而对系统性能影响较小的元件采用相对简单的传递函数表达。本文以一阶传递函数表示用于控制比例泵斜盘倾角的比例阀，控制比例泵斜盘倾角的比例阀的负载流量Qpv（s）相对于比例阀的输入电压up（s）的传递函数可近似为：

式中：Kpv表示负载压降为零时比例阀的静态流量增益；Tpv表示比例阀的时间常数。

以积分传递函数表示的变量活塞[3]，其比例泵的斜盘倾斜角度αp（s）相对于比例阀的负载流量Qpv（s）的传递函数为：

式中：Av表示变量活塞的有效作用面积；Lp表示变量活塞的中心线到铰接轴中心线沿液压泵轴线方向的距离。

以比例泵的传递函数表示泵本体，比例泵的实际输出流量Q′pp（s）相对于斜盘倾角αp（s）的传递函数为：

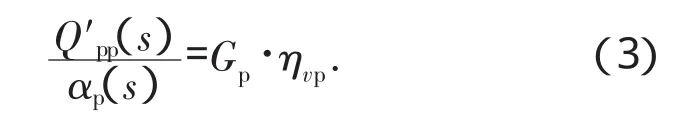
式中：Gp表示比例泵的流量增益；ηvp表示比例泵的容积效率。

主缸对整个系统性能的影响最大，以三阶传递函数表示的主缸的活塞位移xm（s）相对于比例泵的实际输出流量Q′pp（s）的传递函数[4]为：

式中：Am1表示主缸无杆腔活塞的有效作用面积；xm表示主缸活塞的位移；nm表示主缸有杆腔和无杆腔的流量之比；Vmt表示初始等效容积，包括阀、连接管道；CLs表示整个传动回路（从液压泵出口到主缸内）的总（内、外）泄漏系数；M表示液压缸的活塞与拉伸头和负载折算到活塞上的质量之和；B表示液压缸的活塞与负载运动时的黏性阻尼系数；K表示液压缸的活塞与负载的弹簧刚度。若以Kuv表示主缸位移传感器的反馈电压与主缸速度的转换系数，则主缸的活塞位移xm（s）相对于输入电压up（s）的闭环传递函数方框图[5]为（见图2）：

图2　单侧比例泵控制主缸的闭环传递函数方框图

2　伺服阀控制液压缸数学模型的获取（见图3）

图3　单侧伺服阀控制主缸原理框图

主拉伸液压系统中阀控缸部分是以伺服阀控制单出杆柱塞式液压缸的。以一阶传递函数表示伺服阀，伺服阀的负载流量Qsv（s）相对于伺服阀的输入电流信号百分比i%（s）的传递函数为：

式中：Ksv表示负载压降为零时比例阀的静态流量增益；Tsv表示比例阀的时间常数。

若以Kuv表示主缸位移传感器的反馈电压与主缸速度的转换系数，则主缸的活塞位移xm（s）相对于伺服阀输入电流i%（s）的闭环传递函数方框图为（见图4）：

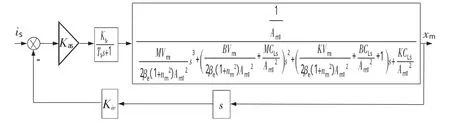
图4　单侧伺服阀控制主缸的闭环传递函数方框图

3　复合控制过程中采用比例泵或伺服阀进行补偿的原理

两主缸在动作过程中主要通过比例泵进行驱动，当两主缸出现不同步现象时，需要通过比例泵或伺服阀进行位移补偿，本次主要采用比例泵单独补偿或伺服阀单独补偿的方式[6-7]。假设主缸1的速度为vm 1、主缸2的速度为vm 2、两主缸的速度差值为Δvm=|vm 1-vm 2|，主缸1的位移为xm 1、主缸2的位移为xm 2、两主缸的位移差值为Δxm=|xm 1-xm 2|，两主缸的起始位移相等。当两主缸出现位置差时，预设置了不同补偿工况的临界参数xm 01～xm 03。当Δxm≥xm 01时采用伺服阀补偿，两主缸的位置差为Δxm≥xm 02且Δxm＜xm 03时采用比例泵补偿，两主缸的位置差为Δxm≥xm 03时认为无法通过补偿实现两主缸同步，不再进行补偿，则xm 03>xm 02>xm 01>0。比例泵和伺服阀的控制框图如下页图5和图6所示，补偿信号均被直接叠加在输入信号上。采用比例泵补偿时补偿信号为原输入信号的Kcp倍，即补偿后的输入信号变为原来的1+ Kcp倍；采用伺服阀补偿时补偿信号为原输入信号的Kcs倍，即补偿后的输入信号变为原来的1+Kcs倍。Kcp和Kcs均取决于补偿量的大小和补偿所用的时间。图6中的选项1或0的原则为：当仅用伺服阀驱动主缸或者采用比例泵和伺服阀同时补偿时为1，伺服阀的补偿量为输入量的百分比；当伺服阀仅用于补偿时为0，输入信号为伺服阀的最大信号，伺服阀的补偿量为输入的伺服阀最大信号的百分比。

4　结语

将该大型铝板拉伸矫直机的主拉伸液压系统的实际参数βe=700MPa、Am1=0.6070m2、Av=18.10cm2、Kpv=2.99 L/（min·V）、Tpv=30 ms、Lp=78.62 mm、Gp= 2199.95L/min、ηvp=96.14%、nm=0、Vmt=437.74 L、B=0 （N·s）/m、K=3.18×108N/m、CLs=2.11 L/（min·MPa）、M=3.70×108kg、Kvw=2.87（V·s）/rad、Kuv=0.754 7（V· s）/mm、Tsv=14ms、Ksv=5.30L/（min·mA）、Kiv=858.4 s/m代入上述模型中可发现，复合控制时预设置不同补偿工况的临界参数xm 01=0.1 mm、xm 02=1 mm、xm 03=3 mm，完全满足了机械规定的主缸拉伸位置同步精度≤±1mm、延伸量控制精度≤0.3%Δ的要求。

图5　比例泵控制主缸方框图

图6　伺服阀控制主缸方框图

在拉伸矫直机的主拉伸液压系统中，以泵控+阀控的复合控制方式控制两侧主缸，在实现了系统的高压、大流量、快速性的同时也保证了主缸的位置控制精度和同步精度，满足了机械上大负载、快速、高精度的要求。同样，通过将实际数据代入上述数学模型的计算可为类似复合控制液压伺服系统的设计和调试提供理论依据。

[1]杨逢瑜.电液伺服与电液比例控制技术［M］.北京：清华大学出版社，2009：4-7.

[2]张莉茹，殷文齐.大型拉伸矫直机液压系统设计分析[J].一重技术，2007（2）：29-30.

[3]Noah D.Manring.Fluid Power Pumps and Motors:analysis,design,and control［M］.New York:mcgraw-hill Professional,2013: 251-266.

[4]罗小梅.电液比例变量泵控马达控制系统的分析研究［D］.西安：长安大学，2005.

[5]刘光临，沈全成，陈奎生.泵控缸速度控制系统动态特性研究[J].液压与气动，2006（2）：38-41.

[6]刘建忠，吴百海，吴小洪，等.泵控与阀控补偿的高精度同步系统的探讨[J].机械开发，1998（4）：15-17.

[7]曹泽生，仲悦，王效亮，等.液压作动系统阀泵联合控制技术研究[J].液压与气动，2013（2）：28-32.

（编辑：贺焱）

Modeling and Application of Compound Control of Hydraulic System

ZHANG Qiang，LI Xianghui，MA Min
（Chinese National Heavy Machinery Research Institute Co.，Ltd.，Xi'an Shaanxi 710032）

Taking the main hydraulic system of a large tension straightening machine as an example,this paper analyzes the method for obtaining each main component model in detail,and gives the mathematical model of pump controlled cylinder and the mathematical model of valve controlled cylinder and the block diagram of the compensation with proportional pump or servo valve in the compound control.Through the calculation of actual data substituted into the above mathematical model,this paper provides theoretical basis for the design and debugging of similar compound control hydraulic servo system.

compound control,pump control cylinder,valve control cylinder

TP273+.3

A

1672-1152（2016）02-0053-03

10.16525/j.cnki.cn14-1167/tf.2016.02.20

2016-01-06

张强（1978—），男，工程硕士，现从事冶金机械设备液压方面的设计与研究工作，工程师。