基于非合作博弈的多小区D2D资源分配算法

张 勇，凌 亚，卢彦博

（1.重庆邮电大学通信新技术应用研究中心，重庆 400065； 2.重庆信科设计有限公司，重庆 400065）

基于非合作博弈的多小区D2D资源分配算法

张 勇1，2，凌 亚1，卢彦博1

（1.重庆邮电大学通信新技术应用研究中心，重庆 400065； 2.重庆信科设计有限公司，重庆 400065）

在蜂窝网络与D2D（设备到设备）网络构成的混合网络中，针对小区内和小区间各用户之间的干扰，研究了多小区D2D通信系统中的资源分配问题，引入非合作博弈理论和定价机制，设计了一种改进的带有干扰因素的效用函数对D2D用户进行功率控制，同时考虑了公平性和系统干扰。通过验证功率控制模型中纳什均衡的存在性和唯一性，得到D2D用户博弈之后的一个稳定状态。仿真结果表明，所提算法不仅能提高用户的公平性，还能提高系统的吞吐量，提升系统性能。

资源分配；设备到设备；非合作博弈；干扰

0 引 言

为了提高频谱利用率，5G（第5代移动通信技术）中提出了D2D（设备到设备）技术［1］，但其会带来严重的系统干扰。目前针对D2D多小区干扰问题的研究比较少［2-3］，本文引进非合作博弈论对D2D混合多小区内的资源进行合理分配，以达到控制系统干扰的目的。

文献［4］提出了一个基于联合频谱分配和功率分配的定价机制，通过分散干扰来保证服务质量，但没有确切的将干扰引入博弈中考虑。文献［5］研究了相邻小区共同的D2D链路通过小区基站之间的博弈来获取资源从而达到均衡。文献［6］研究了多小区中D2D网络的非合作博弈功率控制方法，但建立的效用函数对于功率小于零的情况是不成立的。基于以上分析，本文提出一种改进的基于定价机制的非合作博弈资源分配方法，既考虑通过信道增益来提升公平性，同时也将干扰引进效用函数中。

1 系统模型

一个多小区D2D通信的无线混合系统模型如图1所示。系统采用全频率复用方式进行通信，且每个蜂窝用户分配的资源是正交的，但一个蜂窝用户的资源可以被多条D2D链路复用。本文针对系统存在两条或两条以上的D2D链路且复用相同的资源时产生干扰的情况，提出了一种改进的非合作博弈资源分配方法。

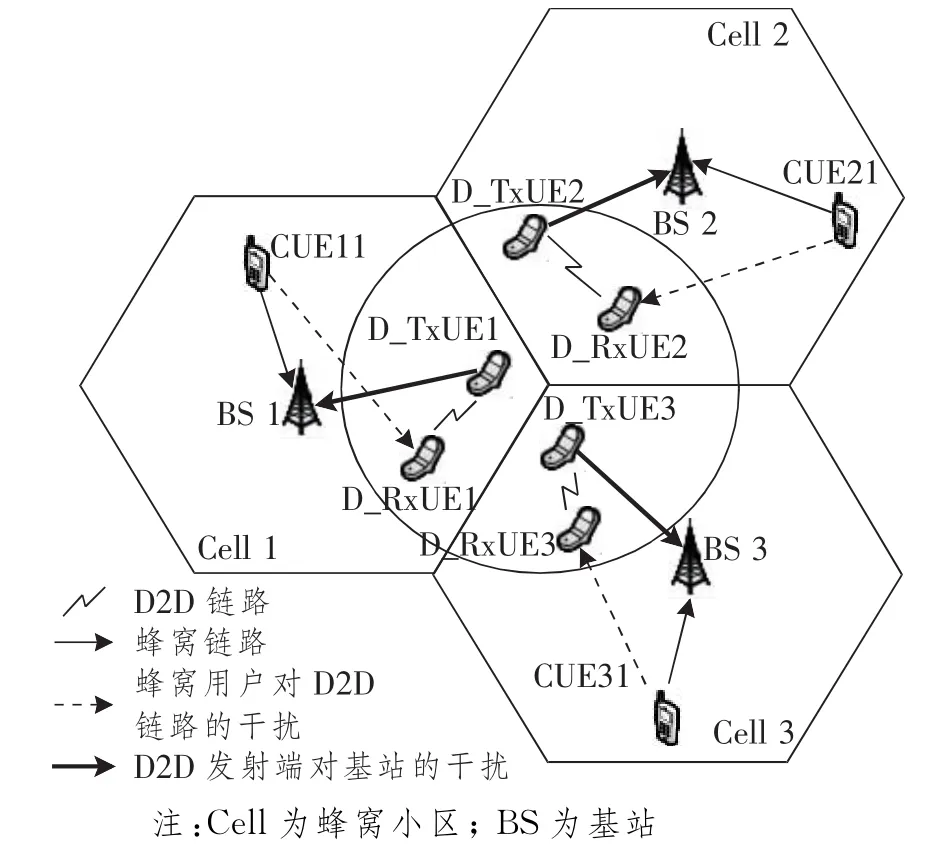
图1　D2D通信无线混合系统模型

设系统包含K个小区，每个小区包含一个BS，Q个随机分布的CU（蜂窝用户），M对D2D链路（D2DTx-D2DRx），总带宽为W，资源块数目为T。则D2D接收端的SINR（信干噪比）为

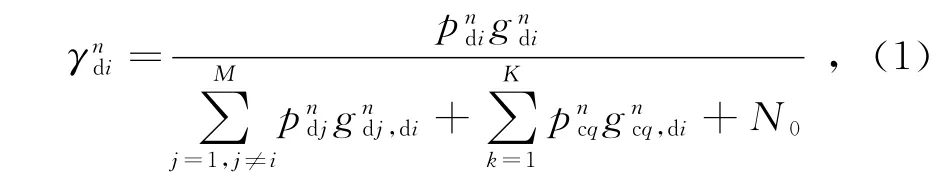
式中，pndi为复用第n个蜂窝用户和D2D用户的发射功率；pndj为除了第i个D2D链路之外复用同样蜂窝用户资源的D2D链路；gndi、gndj，di、gncq，di分别为各条链路的增益，N0为信道噪声。

2 基于非合作博弈的资源分配算法

基于以上分析，D2D链路功率的收益函数可表示为

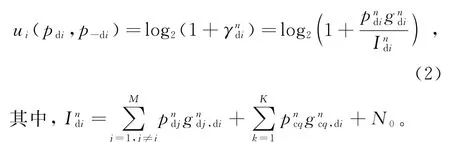
每一个参与博弈的用户都希望自身利益最大化，为了防止各用户因过分提高自身功率而对其他使用相同资源的用户造成较大的干扰，需要引入定价机制对其实施惩罚，使得其在竞争资源时折衷考虑其效用与代价。定价函数的引入可以隐含地使用户合作却不改变功率控制的非合作特性，同时还能提高系统性能。基于此，为复用资源n的D2D链路设计定价函数如下：

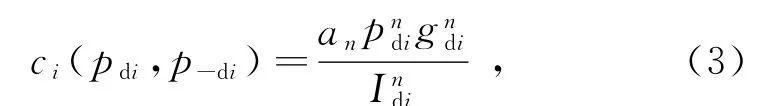
则博弈参与者的净效用函数为

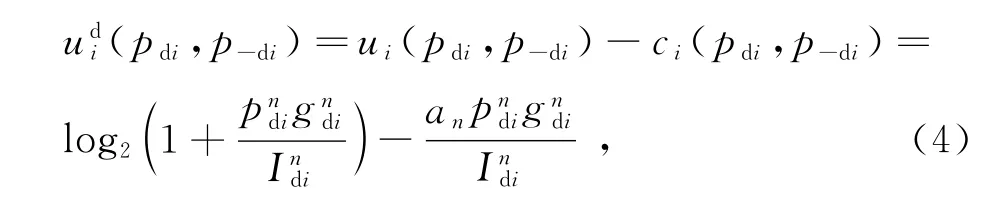
式中，an表示博弈用户的功率定价因子。与传统的线性定价函数不同，式（4）不仅定价了博弈参与者的功率，引入了信道增益来提升系统公平性，还考虑了其他使用相同资源的用户对当前博弈用户的干扰这一因素。当用户受到其他用户的干扰较大时，应降低惩罚；反之，应增大惩罚。考虑到多小区D2D复用模式的特性，参与博弈的D2D链路越多，系统内的干扰就越大越复杂。令式（4）的一阶导数为零，可得用户的最优功率响应满足

则参与博弈的D2D链路最优响应函数为

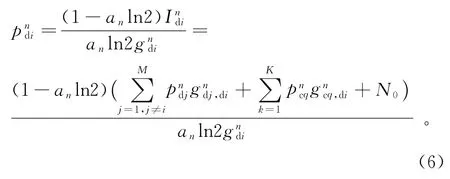
2.1纳什均衡的存在性

对于本文提出的NPAGP-I（考虑干扰的非合作功率分配博弈）算法，分析如下：（1）D2D链路数目有限，参与者集合Q是一个有限集；（2）博弈参与者i在资源n上的策略空间为Pndi=［0，pnmax］，显然Pndi是正实数空间R+上的一个非空的、闭的凸集；（3）博弈参与者i的效用函数udi（pi，p-i）在策略空间Pndi=［0，pnmax］是连续的［7］。用户udi的净效用函数对pndi的二阶偏导数为

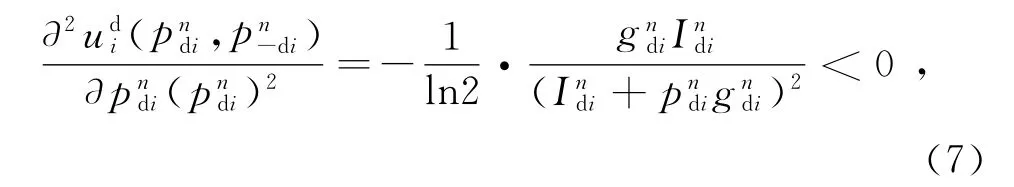
可得udi（pndi，pn-di）对pndi是凹的，且是拟凹函数，则存在NEP（纳什均衡点）。

2.2纳什均衡的唯一性

由最优响应函数pndi≥0可得an的取值范围为an≤1/ln2。要证明NEP的唯一性，关键是证明最优响应函数是标准函数值，即满足正性、单调性和可测量性。由an的取值范围可以保证功率求解表达式大于0，即满足了正性。

由pndi的表达式可知，由于某个D2D链路的自身发射功率与复用相同资源的其他D2D链路和蜂窝用户的干扰发射功率有关，则可令P=A（P）。设P≥P′，则有

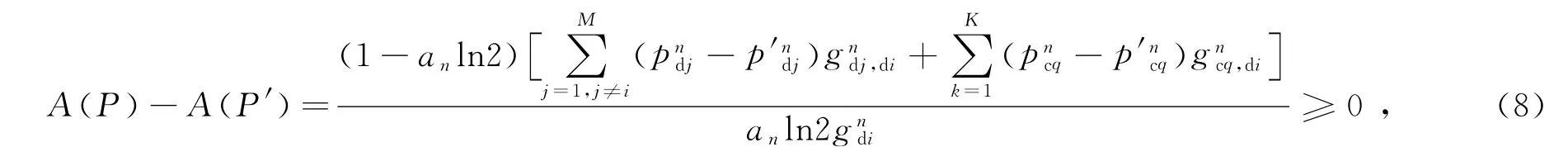
则表达式为递增函数，且当P=P′时取等号。

证明可测量性，即是要证明对 ∀λ＞1，有λA（P）≥A（λP）。由于

因此表达式满足可测量性。故存在唯一的NEP。

2.3考虑干扰的分布式功率迭代算法实现

本文中蜂窝用户采用的是轮询调度方法，而对于D2D用户，采用的是基于本小区内最大SINR的用户调度方案。用户调度完成后，将按照以下步骤实现功率迭代算法：

（1）t=0时，D2D链路以各发射节点所分配到资源块上的平均最大发射功率作为各资源块上D2D发射端的初始化功率pnk，di，max=pnk，max/T，n∈｛1，2，…，T｝；

（2）将上一次迭代所得到的在资源n上的发射功率pndi（t）代入式（6），得到更新后新的发射功率pndi（t+1）；

（3）判定|pndi（t+1）-pndi（t）＜η|是否成立，其中η为迭代精度（无限接近于0的极小值），若超过设置的最大迭代次数，则迭代直接结束；若结果不成立，但是处于迭代次数范围之内，则令t=t+1，重复步骤（2）。

3 仿真分析

为了验证所提算法的性能，采用Matlab软件进行算法仿真实现。考虑一个3小区的D2D通信混合网络场景。仿真参数设置如下：系统带宽为10MHz，小区的站间距为500m，各小区内随机分布10个蜂窝用户，5对D2D用户，蜂窝用户的最大发射功率为23dBm，D2D用户最大发射功率为10dBm；系统的热噪声密度为-174dBm/Hz。蜂窝链路的路损模型为128.1+37.6lgd；D2D链路的路损模型为：148+40lgd。

图2所示为不同惩罚因子下D2D用户吞吐量的变化趋势。由图可知，随着功率惩罚因子的增大，D2D用户的吞吐量呈现先增长后下降的趋势，这是因为各用户最初都以较小的发射功率进行通信，相互之间干扰较小，使得吞吐量提升。而随着惩罚因子超过最佳值时，各用户功率慢慢增大，干扰也随之增大，使得吞吐量开始逐渐下降。惩罚因子为0.7时，系统中D2D用户的吞吐量达到最大值。

图2　不同惩罚因子下D2D用户吞吐量的变化趋势

在仿真过程中，将本文所提NPAGP-I算法与其他几种不同的算法作了性能对比，包括EPA（功率均分）和考虑功率平方定价机制的NPAGP-P2（非合作功率分配博弈）［7］。

图3所示为各用户的公平性指数。由图可见，相比于EPA，NPAGP-P2和NPAGP-I两种算法公平性指数较高，这是因为NPAGP-P2和NPAGP-I算法的效用函数引入了信道增益，对信道条件不同的用户进行了区分考虑，以免造成信道条件越好的用户所分配的资源越多。而NPAGP-I算法在效用函数中还多引入了干扰因素，对于干扰大的用户惩罚更大，同理，干扰小的用户惩罚小，因此公平性要优于NPAGP-P2。同时，在进行D2D通信时，必须首先保证蜂窝用户的通信，所以蜂窝用户公平性的提升要明显很多。

图3　不同算法下各用户的公平指数

图4所示为不同算法下各小区吞吐量的比较。对比EPA算法，由于NPAGP-P2与NPAGP-I两种算法是基于非合作博弈模型进行功率分配，通过对惩罚因子的调整，在考虑自身惩罚代价的前提下，通过功率的迭代达到一个最稳定的状态，在一定程度上也降低了小区内和区间干扰，从而使系统吞吐量得到提升。由于在自适应调整功率时，功率上下的幅度并不大，所以吞吐量之间的差异较小。

图4　不同算法下各小区吞吐量

图5所示为几种不同算法下D2D吞吐量的CDF（概率累积函数）曲线。NPAGP-P2和NPAGP-I算法通过博弈模型对参与者的功率进行自适应控制，因此相互之间的干扰也会自适应调整，这两种算法吞吐量的提升比EPA算法高，且NPAGP-I算法由于对干扰进行直接控制，因此吞吐量提升更明显。由于博弈过程中功率变化将导致干扰的变化，通信过程中会出现干扰不可控的情况，所以相比于EPA算法NPAGP-P2和NPAGP-I两种算法的CDF曲线要弯折一些。

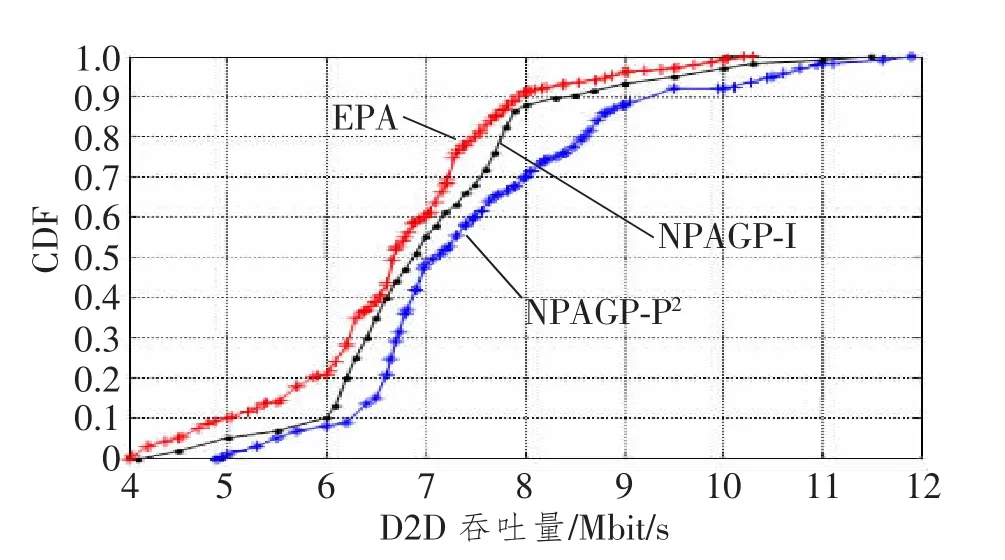
图5　不同算法下D2D吞吐量的CDF曲线

4 结束语

随着D2D系统在无线通信网络的广泛应用，干扰问题成为人们关注的重点。博弈论作为通信领域的一个重要研究方法，在D2D通信中的应用也越来越广泛。本文采用了博弈论中的非合作博弈方法对多小区内的D2D通信资源分配问题进行了研究。在建立非合作博弈模型之后，引入定价机制，采用带有干扰因素的效用函数对D2D链路的功率进行迭代运算，通过证明纳什均衡的存在性和唯一性，得出功率的稳定值。仿真结果表明，本文所提算法通过对干扰的惩罚，提高了系统的公平性和用户吞吐量。

［1]Doppler K，Rinne M，Wijting C，et al.Device-to-device communication as an underlay to LTE-Advanced networks［J］.Wireless Communicati-ons，IEEE，2009，47（12）：42-49.

［2]Xu Shaoyi，Wang Haiming，Chen Tao.Effective Interference Cancellation Mechanisms for D2DCommunication in Multi-Cell Cellular Networks［C］//VTC 2012. Yokohama，Japan：IEEE，2012：1-5.

［3]程永生，董宇涵，张学聃.多小区CDMA系统D2D通信上行性能研究［J］.计算机工程，2013，（07）：11-15.

［4]杨春刚，李建东，李维英.认知无线电中基于非合作博弈的功率分配方法［J］.西安电子科技大学学报，2009，（01）：1-4，27.

［5]Yin Rui，Yu Guanding，Zhang Huazi，et al.Pricing-Based Interference Coordination for D2DCommunications in Cellular Networks［J］.IEEE Transactions on，2015，14（3）：1519-1532.

［6]Huang Jun，Zhao Yanxiao，Sohraby K.Game-Theoretic Resource Allocation for Intercell Device-to-Device Communication UnderlayingCellular Network［C］// NWRCS 2014.Shanghai，China：IEEE，2014：79-83.

［7]陈华梁，吴丹，田辉.博弈论在无线通信中的应用专题讲座（二）第3讲D2D网络中一种非合作博弈功率控制方法［J］.军事通信技术，2013，（4）：82-88.

Resources Allocation Algorithm for Multi-cell D2D Based on Noncooperative Game Theory

ZHANG Yong1，2，LING Ya1，LU Yan-bo1
（1.Research Centre for Application of New Communication Technologies，Chongqing University of Posts and Telecommunications，Chongqing 400065，China； 2.Chongqing Information Technology Designing CO.，LTD.，Chongqing 400065，China）

In the mixed network which consists of cellular and device-to-device，there is a dynamic resources allocation problem in multi-cell D2Dcommunication system when the interference between the users of intra-cell and inter-cell is considered.In this paper，we design a utilityfunction with interference control of the transmitted power of D2Dusers after introducing the non-cooperative game theory and pricingmechanism.This utilityfunction not only considers the fairness but also the interference of the system.Then we demonstrate the existence and uniqueness of Nash equilibrium in a power control model，which indicate that the D2Dusers can achieve a stable state after the games.Simulation results show that the proposed algorithm not only improves the fairness among the users，but also increases the throughputs and improves the performances of the system.

resource allocation；device-to-device；non-cooperative game theory；interference

TN929.5

A

1005-8788（2016）02-0075-04

10.13756/j.gtxyj.2016.02.023

2015-08-05

张勇（1970-），男，重庆长寿人。高级工程师，硕士，主要研究方向为通信新技术应用。