计时攻击研究与仿真

2016-10-09贾徽徽王潮顾健宋好好唐迪

网络与信息安全学报 2016年4期

关键词：计时密钥比特

贾徽徽，王潮，顾健，宋好好，唐迪

（1. 公安部第三研究所，上海 200031；2. 上海大学特种光纤与光接入网省部共建重点实验室，上海 200072）

计时攻击研究与仿真

贾徽徽1，王潮2，顾健1，宋好好1，唐迪1

（1. 公安部第三研究所，上海 200031；2. 上海大学特种光纤与光接入网省部共建重点实验室，上海 200072）

借助于隐马尔可夫模型思想，提出了一种针对采用“倍点—点加”点乘算法的椭圆曲线数字签名体系的一种计时攻击方法，并对美国国家标准与技术研究院（NIST）公布的二进制域上的5条Koblitz安全曲线进行了攻击仿真实验，成功地攻击了除K-571以外的其他4条Koblitz安全曲线。对于每一条安全曲线仅采集一次时间数据、耗时几十分钟就能恢复出几乎全部的密钥比特，实验结果表明，该方法实施简单、成功率高，是对当前安全曲线有较大威胁的一种侧信道攻击手段。

侧信道攻击；计时攻击；隐马尔可夫模型；椭圆曲线密码

1　引言

安全是计算机和通信系统长期以来一直关注的问题，大量的研究工作也一直致力于解决这个问题。密码算法构成了可以作为构建模块来构造针对特定目标的安全机制的原始材料，这些算法包括对称密码、公钥密码以及散列函数等。椭圆曲线密码（ECC，elliptic curve cryptography）是1985年由Koblitz和Miller提出的一种公钥密码体制［1］，有安全性高、占用带宽小、密钥长度短、计算速度快等特点，已被广泛应用于无线通信、密码芯片、电子商务等领域，也是卫星网络、物联网等新型网络的首选，因此，对其安全性的研究显得尤为重要。ECC的安全性建立在椭圆曲线离散对数问题（ECDLP，elliptic curves discrete logarithm problem）的困难性之上，1999年9月28日，加拿大的Certicom公司宣布利用法国、澳大利亚、加拿大、美国、芬兰、奥地利等国家的760台计算机成功解决了97 bit的ECDLP问题。在解决问题过程中一共进行了130 000亿次椭圆曲线“点加”运算。2002年11月6日，Chris Monico博士带领NotreDame大学数学研究中心的数学家利用10 000台计算机每天工作24 h，历时549天才成功地完成了Certicom公司的109 bit P曲线的挑战，109 bit也是目前传统攻击的最高挑战比特数。对于NIST公布的ECC安全曲线中最小的163 bit密钥长度来说，以目前计算机的计算速度进行穷举攻击大约需要1012年，这证明ECC算法确实具有极高的安全性。

但事实上，密码算法不是决定整个密码安全性的唯一因素，密码算法的实现需要依附一个软件或者硬件设备平台，在这些设备运行过程中会与周围环境发生交互并受周围环境的影响。攻击者可以通过监测这些物理交互作用找出可以用于密码分析的有效信息，这种信息就被称为侧信道信息，而攻击利用侧信道信息进行攻击的方法就被称为侧信道攻击（SCA，side channel attack）。所谓侧信道攻击是指攻击者采集密码设备实现过程中内部状态无意泄漏的物理效应并进行分析，典型的侧信道攻击包括计时攻击［2］、功耗攻击［3］、电磁分析攻击［4］、Cache攻击［5，6］、故障攻击［7，8］、扫描式攻击［9］等。

计时攻击是利用密码算法在执行过程中泄漏出来的时间信息来进行攻击的，由于要考虑性能优化问题，密码算法往往会使用一些分支语句、条件语句等来加快执行速度，但也同时给加解密时间带来了差异，这些差异可能会泄漏一些重要信息，计时攻击就是利用这种差异来推测密钥信息的。计时攻击不需要额外的硬件设备，既可在本地实现，也可以在远程网络中实现，并且由于计时攻击所需要的时间差异信息来源于密码算法本身，因此，攻击威胁力比较大，是目前侧信道研究的热点之一。需要强调的是这种攻击方法主要适用于RSA、ECC等公钥密码。

1996年，Kocher首次提出了计时攻击的概念［2］，并成功地对 RSA模指数运算实施了攻击；之后Schindler对基于CRT算法的RSA进行了攻击［10］，其主要思想是利用 Montgomery算法运算时发生的额外约减所泄漏出来的时间差异来推测密钥。

OpenSSL是一个开放源代码的SSL实现，主要用来实现通信的高强度网络加密，现在被广泛应用于各种网络应用程序中。斯坦福大学的Brumley等展示了怎样用计时攻击恢复出OpenSSL 中RSA密码算法的私钥信息［11］，对Kocher提出的计时攻击方法进行了改进并对运行 OpenSSL的服务器实施了远程攻击，通过 30多万次的访问，2 h左右恢复出了1 024 bit的RSA密钥。Canvel设计出了一种针对SSL和TLS中的CBC加密体系的计时攻击方案［12］，可以解密一些简单的密文。

Cachalo等提出了针对欧洲 NESSIE项目中GPS识别体系的计时攻击［13］，仅用800次测量数据，耗时几秒钟就恢复出了其中的密钥，成功率高达80%。Sakruai通过观测解密谕言时丢弃信号的时间，提出了针对EROC-2公钥密码体制的一种计时攻击［14］，这种公钥密码体制被证明是非常安全的，并被写入了IEEE P1363标准中，目前很多国际密码标准组织将EPOC作为公钥密码的候选算法。Levine等提出了针对低延时混合基系统的计时攻击［15］，这些系统是一些企图掩盖输入和输出信息之间对应关系的通信代理服务器，他们还提出了一种新的技术来抵御这种计时攻击。匈牙利人Rudolf等提出了一种重建密钥方法高级计时攻击［16］，利用统计学上方差分析和t检验方法对采集到的时间数据进行分析，成功地恢复出了128 bit的RSA密钥。

通过对计时攻击的研究发现，计时攻击主要应用在RSA公钥密码上，针对ECC的计时攻击目前还没有相关文献，本文基于隐马尔可夫模型（HMM，hidden Markov model）思想，以HMM为框架，提出了一种针对椭圆曲线数字签名算法（ECDSA，elliptic curve digital signature algo-rithm）的计时攻击方案，对NIST公布的5条二进制域上的 Koblitz安全曲线实施了攻击仿真实验，解决了在实验过程中遇到的3个关键性技术问题，成功地攻击了5条安全曲线中除K-571以外的其他4条曲线。针对这种攻击，本文还提出了相应的防御措施，并展望了针对ECC的计时攻击在今后的发展，为以后实施物理攻击做好铺垫。

2　ECC基本知识

ECC的核心运算是椭圆曲线上的点乘运算Q=kP，这种令椭圆曲线上的一个非零点P重复相加k次的操作称为标量乘法，它决定着椭圆曲线密码体制的运算速度。为了提高ECC的加解密速度，密码学家们提出了许多计算点乘运算的算法，基于二进制的“倍点—点加”（double-and-add）算法就是被广泛应用的一种点乘算法，算法描述如下。

从算法1中可以看出，当ik为0或1时，执行的运算量不同，泄漏出来的信息就是运算的时间不同，本文正是利用这个时间信息来进行计时攻击的。

由于 ECC私钥的使用只发生在解密和数字签名过程中，因此，计时攻击也只能在这2个过程中使用，本文选取在椭圆曲线数字签名（ECDSA）过程中使用计时攻击来获取私钥。数字签名的算法描述如下。

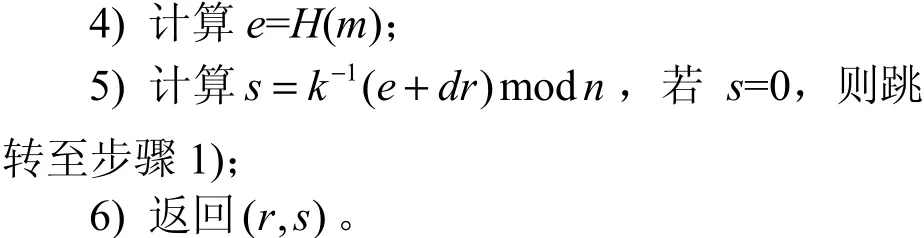
其中，P为基点，m为要签名的消息，H表示一个密码杂凑函数，k为产生的随机数，称之为临时密钥，d为私钥，（r，s）表示签名。

3　隐马尔可夫模型

隐马尔可夫模型（HMM）是马尔可夫链的一种，它的状态不能直接观察到，但能通过观测向量序列观察到，每个观测向量都是通过某些概率密度分布表现为各种状态，每一个观测向量是由一个具有响应概率密度分布的状态序列产生。自20世纪80年代以来，HMM被应用于语音识别，取得了重大成功。到了20世纪90年代，HMM还被引入计算机文字识别和移动通信核心技术“多用户的检测”。近年来，HMM在生物信息科学、故障诊断、密码分析等领域也开始得到应用。HMM和侧信道攻击的结合早有应用，2003年，Chris Karkof等第一次将HMM用于密码分析上［17］，并提出了一个用于恢复密钥的有效算法；2005年，Green等［18］对HMM在密码分析上的应用做了进一步研究，提出了将HMM和启发式搜索相结合来进行密码分析的思想；2009年，在亚密会上，Brumley等［19］提出了一种Cache计时模板攻击架构，将HMM和向量量化理论运用到了Cache攻击中，实现了针对ECC的攻击，对于160 bit的密钥，使其平均复杂度由2160降低到248。本文提出的HMM与计时攻击的结合还是首次。HMM涉及到的一些参数描述［20］如表1所示。

表1　HMM的参数描述

在HMM的实际应用中有3个中心问题需要解决，具体如下。

2）解码问题：对于给定模型和观察值序列，求可能性最大的隐含状态序列。

3）学习问题：对于给定的一个观察值序列，调整参数λ，使观察值的输出概率P（O|λ）最大，也就是用给定的观察值去训练HMM模型，优化模型参数。

本文要解决的是HMM的3个中心问题中的解码问题。利用HMM进行侧信道攻击的基本思想是通过密码算法泄漏出来的侧信道信息对未知密钥比特序列进行猜测，而HMM的解码问题是指通过对观察到的序列分析猜测未知状态序列，两者有相似的地方，可以建立这样一个HMM模型，其中，未知状态序列就是密钥bit序列，而观测序列就是指通过侧信道获取的观测信息，在本文中是指通过侧信道获取的计时信息。

4　基于HMM的计时攻击方案

计时攻击首先由Kocher于1996年提出，并成功对RSA模指数运算进行了攻击，其基本原理是利用密码算法在加解密过程中泄漏出来的时间信息来进行攻击的。密码系统加解密时间差异信息产生的来源为性能优化、分支运算、条件语句、RAM Cache命中、运行时间不固定的处理器指令以及其他多变的原因。

在double-and-add算法中，由于if语句的存在使密钥比特为0或1时执行的操作步骤不同，比特为1时比比特为0时要多一步“点加”运算，最终表现出来的是比特为0或1时的执行运算时间不同，这就为实施计时攻击提供了可能性。

由算法2可知，在步骤2）中有点乘运算，所以可以利用计时攻击在计算 kP点乘运算时求出临时密钥k，临时密钥在每次签名都不同，因此，一次签名只能采集一次计时数据，这也是计时攻击难点所在。由于H（m）、签名s已知，就可以利用式（1）求出私钥d。

所以，针对ECDSA攻击的关键就是利用获取的计时数据求解临时密钥k。基于HMM思想，本文首先建立double-and-add标量乘法的HMM，如图1所示。

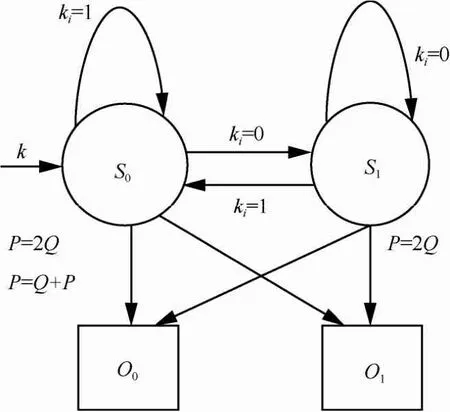
图1　double-and-add标量乘法的HMM

假设临时密钥k=26，通过编写程序采集到的时间数据从最高位到最低位依次是t1=0.000 189 668 s，t2=0.156 695 s，t3=0.070 859 s，t4=0.147 188 s，t5=0.056 313 2 s，因为观察到5组数据，那么可以推测密钥的长度l=5，分别对应k4到k0，最高位k4=1是已知的，那么第一个数据就舍弃不用，通过余下的4个数据来推测剩余的密钥比特。比较数据发现：第一个数据t1明显比其他几个要小好几个数量级，这是必然的，因为执行第一次循环，Q的初始值为0，它其实是执行的0+P的运算，没有用到大数运算中的“点加”运算，所需时间较少。在后面4个数据中，t2和t4大小相近并远大于t3和t5，结合算法分析，时要比时多执行一次“点加”运算，不难推测出t2和t4是ki=1时算法的执行时间和是时算法的执行时间，也就是，推测结果与原始密钥一致，说明破解成功。

5　ECDSA计时攻击的仿真实现

5.1仿真实验过程中的关键技术

1）精度问题

计时攻击主要通过对执行时间的监测来推算密钥，由于差异值一般都很小，因此需要高精度精确计时技术。本文采用的是windows.h库中获取机器内部时钟频率的QueryPerformanceFrequency（）函数和 QueryPerformanceCounter（）函数。在定时前应该先调用 QueryPerformanceFrequency（）函数获得机器内部计时器的时钟频率，接着在需要严格计时的事件发生前后分别调用QueryPerformanceCounter（）函数，利用2次获得的计数之差和时钟频率就可以计算出事件经历的精确时间，利用这2个函数可以将计时时间精确到微秒级，满足实验所需要的精度要求。

2）阈值问题

由于受到噪声、Cache命中失效、CPU资源利用率等因素的影响，每次执行得到的计时数据都不尽相同，都有一个小范围的波动，因此，这里有一个阈值选择的问题，阈值过大或过小都影响实验结果，阈值一旦确定不准确就会对后面比特信息的判断产生直接影响。对于不同安全级别的曲线，对应阈值就有很大的差异，本文采用的是统计学方法，通过上百次的计算得出K-283安全曲线，“倍点—点加”运算平均耗时为0.205 537 s，“倍点”运算平均耗时为0.101 148 s，取阈值r=然后从次高位开始逐一判断（最高位为1无需判断），如果比特对应的计时时间大于r=0.153 323 s，此比特就确定为1；反之，如果比特对应的计时时间小于r=0.153 323 s，就确定为0。

3）错误比特值确定

由于外界环境以及CPU本身的影响，在判断密钥比特信息时会存在一定的误差，并不能保证每次都能恢复出全部的密钥比特数，而且对于ECDSA签名，临时密钥都是随机选取，也就是说每次的临时密钥都不相同，因此，只有一次采集时间数据的机会，如果攻击失败，怎样从已获取的临时密钥中快速找出错误的比特从而破解密码系统是一个非常关键的技术问题。

在实验过程中发现，猜测出的临时密钥偶尔会出现1个或2个错误比特的情况。虽然错误比特数较少，但是对于传统的方法，如果有1个错误比特，最多需要进行N（临时密钥长度）次搜索，复杂度为O（ N），如果有2个错误比特，需要进行N（N-1）次搜索，复杂度为为了降低其搜索的复杂度，本文提出使用Grover算法进行搜索以降低复杂度。Grover算法是在第28届美国计算机学会举办的计算理论国际会议上提出的一种量子搜索算法［21］，它将问题的搜索步数从经典算法的N缩小到起到了对经典算法的二次加速作用，从而显著地提高了搜索的效率。在猜测的临时密钥中，如果只有一个错误比特，那么只需要次搜索就可以找出来，如果有M个错误比特，也仅需要搜索即可，

对于长度为256 bit的临时密钥，如果只有一个错误比特，根据量子Grover搜索理论最多进行 16次搜索就能找出，而利用穷举搜索，最多需要进行256次搜索，搜索效率明显得到提高。

5.2仿真实验及结果分析

实验环境为Intel Core2 Duo CPU T6570 2.10 GHz，内存2 GB，编程环境为Microsoft Visual Studio C++ 2005。实验对象为 NIST推荐的二进制域上的 5 条Koblitz安全曲线，以K-283为例，其安全曲线参数如表2所示。

3）对输出进行测量，观察结果为Sv，若

表2　NIST推荐的K-283安全曲线参数

其中，Gx、Gy为基点的横纵坐标，临时密钥k随机选取并取值为

针对ECDSA的计时攻击流程如图2所示。

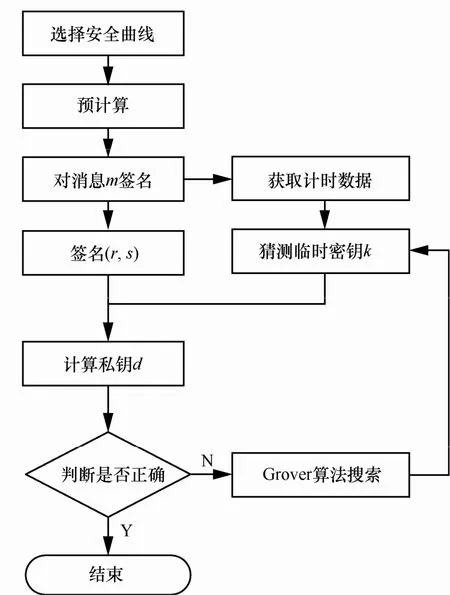
图2　计时攻击流程

根据流程图编写C++程序，当对消息m签名时，在源程序中植入QueryPerformanceFrequency（）和QueryPerformanceCounter（）2个函数，在定时前应该先调用QueryPerformanceFrequency（）函数获得机器内部计时器的时钟频率，接着在密钥比特执行循环运算前后分别调用QueryPerformanceCounter（）函数，利用2次获得的计数之差和时钟频率就可以计算出事件经历的精确时间，也就是执行一次密钥比特运算所消耗的时间。采集有关计时数据，得到一组时间数据序列，然后将得到的时间数据序列与先前确定出的阈值进行比较，得到一个二进制比特序列，也就是猜测出的临时密钥，实验仿真如图3所示。

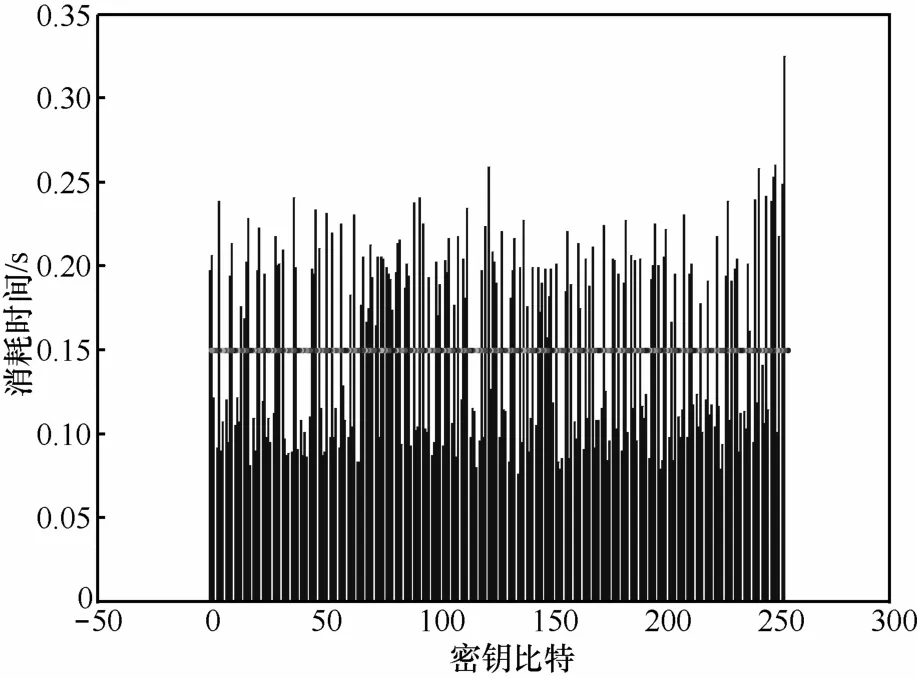
图3　double-and-add算法计时攻击仿真（256 bit密钥）

通过对仿真图分析后得到的猜测密钥为

经比对，猜测密钥k'与原始临时密钥k完全一致，说明本次实验攻击成功。

本文提出的计时攻击是根据点乘算法中算法不同带来的时间差异信息进行的攻击，并结合HMM 模型进行了侧信道攻击的仿真，对使用double-and-add算法的加密算法仅耗时几十分钟就可以恢复出全部的密钥，可以看出计时攻击对密码安全性的强大威胁。预防此类攻击的方法就是消除点乘算法中表现出来的时间差异，称之为“盲化技术”，其中较流行的是Montgomery点乘算法，具体如下。

Montgomery算法最大的特点就是密钥的比特无论是0还是1都执行相同的运算，也就是说ki为0或1时的加密时间几乎是相同的，因此，可以有效地防御计时攻击。通过本文提出的计时攻击方法对采用Montgomery点乘算法的密码系统进行攻击得到的结果如图4所示。

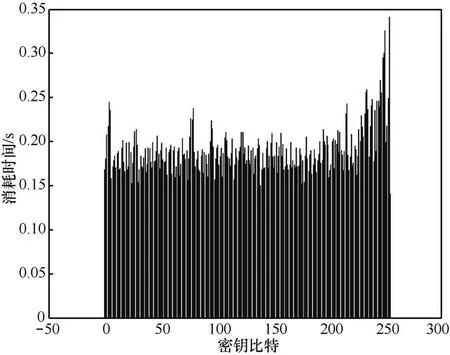
图4　Montgomery算法计时攻击仿真（256 bit密钥）

通过图4可以看出，计时攻击所得到的时间信息相差无几，很难通过时间差异来推测密钥，所以，Montgomery点乘算法能够很好地防御本文提出的时间攻击。

6　结束语

计时攻击是最早被提出来的侧信道攻击方法，也是在侧信道攻击中少有的不用通过其他的辅助硬件就能实现的攻击方法，攻击成本较低，易于实现。但是国内对计时攻击的研究还处于初级阶段，而且大部分都是针对RSA公钥密码的攻击，针对ECC方面的研究分析几乎还没有涉及。本文基于HMM思想提出来了一种针对ECDSA的计时攻击方法，并编程对NIST公布的安全曲线进行了仿真实验，解决了实验过程中存在的 3个关键技术问题，仅耗时几分钟就能恢复出几乎全部的临时密钥比特值，对当前密码的安全性具有极大的威胁。消除点乘算法中的时间差异是抵御时间攻击最有效的方法，因此，研究构造能够抵御时间攻击并且加密速度又快的点乘算法具有重要现实意义。本文提供的仿真实验方法可以为以后研究有关计时物理实验攻击提供一些借鉴，实施计时物理实验攻击也是下一步要研究的内容。侧信道攻击的提出为密码设计者提供了更高的要求，要求设计出来的密码系统除了能够抵御传统的数学攻击外还要抵御来自各个侧信道方向的攻击，只有这样的密码系统才称得上是一个安全的密码体统。

［1］KOBLIZ N. Elliptic curve cryptosystems［J］. Mathematics of Computing American Mathematical Society，1987，48（48）： 203-309.

［2］KOCHER P C. Timing attacks on implementations of diffie-hellman，RSA，DSS and other systems［C］//International Cryptology Conference on Advances in Cryptology. c1996：104-113.

［3］KOCHER P，JAFFE J，JUN B. Differential power analysis［C］//The 19th Annual International Cryptology Conference on Advances in Cryptology.c1999：388-397.

［4］QUISQUATER J J，SAMYDE D. Electromagnetic analysis（EMA）：measuresand counter measures for smart cards［C］//The International Conference on Research in Smart Cards： Smart Card Programming and Security. c2001：200-210.

［5］PADE D. Theoretical use of cache memory as a cryptanalytic side-channel［R］. Department of Computer Science，University of Bristol，2002.

［6］赵新杰，郭世泽，王韬. 针对AES和CLEFIA的改进Cache踪迹驱动攻击［J］. 通信学报，2011，32（8）： 101-110. ZHAO X J，GUO S Z，WANG T，et al. Improved cache trace driven attack on AES and CLEFIA［J］. Journal on Communications，2011，32（8）：101-110.

［7］BONEH D，DEMILLO R A，LIPON R J. On the importance of checking cryptographic protocols for faults［J］. Journal of Cryptology，2001，14（2）： 101-119.

［8］张金中，寇应展，王韬. 针对滑动窗口算法的椭圆曲线密码故障分析［J］. 通信学报，2012，33（1）： 71-78. ZHANG J Z，KOU Y Z，WANG T. Elliptic curve cryptosystem fault analysis on the sliding window algorithm［J］. Journal on Communications，2012，33（1）：71-78.

［9］YANF B，WU K J，KARRI R. Scan-based side-channel attack on dedicated hardware implementations of data encryption standard［C］//IEEE International Test Conference（ITC）. c2004： 339-344.

［10］SCHINDLER W. A timing attack RSA with the Chinese remainder theorem［C］//Lecture Notes in Computer Science（LNCS）. c2000：109-124.

［11］BRUMLEY D，BONEH D. Remote timing attacks are practical［J］. Computer Networks，2005，48（5）： 701-716.

［12］CANVEL B，HILTGEN A，VAUDENAY S. Password interception in a SSL/TLS channel［J］. Information Technology Journal，2003，2729（3）：583-599.

［13］CATHALO J，KOEUNE F，QUISQUATER J J. A new type oftiming attack： application to GPS［M］//Berlin Heidelberg： Springer，2003：291-303.

［14］SAKURAI K，TAKAGI T. A reject timing attack on an IND-CCA2 public-key cryptosystem［C］//The 5th International Conference on Information Security and Cryptology. c2002：359-373.

［15］LEVINE B N，REITER M K，WANG C，et al. Timing attacks in low-latency mix systems［M］//Berlin Heidelberg： Springer，2004：251-265.

［16］TOTH R，FAIGL Z，SZALAY M. An advanced timing attack scheme on RSA［C］//The 13th International IEEE Telecommunications Network Strategy and Planning Symposium. c2008：1-24.

［17］KARLOF C，WAGNER D. Hidden Markov model cryptanalysis［C］//Lecture Notes in Computer Science（LNCS）.c2004：17-34.

［18］GREEN P J，NOAD R，SMART N P. Further hidden Markov model crytannalysis［M］//Berlin Heidelberg： Springer，2005：61-74.

［19］BRUMLEY B B，HAKALA R M. Cache-timing template attacks［C］//Lecture Notes in Computer Science（LNCS）. c2009：667-684.

［20］RABINER L R. A tutorial on hidden Markov models and selected applications in speech recognition［J］. Proceedings of the IEEE，1989，77（2）： 257-289.

［21］GROVER L. A fast quantum mechanical algorithm for database search［C］//ACM Symposium on Theory of Computing. c1996：212-219.

Research and simulation of timing attacks on ECC

JIA Hui-hui1，WANG Chao2，GU Jian1，SONG Hao-hao1，TANG Di1

（1.The Third Research Institute of Ministry of Public Security，Shanghai 200031，China；2. Shanghai University Key Lab of Specialty Fiber Optics and Optical Access Network，Shanghai 200072，China）

Based on the hidden Markov model（HMM）idea，a timing attack on the elliptic curve digital signature system，which adopted the “double-and-add” scalar multiplication，was proposed. Simulation experiments on the secure Koblitz curve which released by the National Institute of Standards Technology（NIST）were implemented and four secure Koblitz curves except the K-571 were attacked successfully. The experiment results show that the attack can recover almost all the key bits in a few minutes by collecting only once time data，and is easy to implement at a high success rate.

side channel attack，timing attack，hidden Markov model，elliptic curve cryptography

TP309.7

10.11959/j.issn.2909-109x.2016.00025

2016-01-25；

2016-02-07。通信作者：贾徽徽，jiahh@mctc.org.cn

国家自然科学基金资助重点项目（No.61332019）；国家自然科学基金资助项目（No.61572304，No.61272056）；上海科委科技创新行动计划技术标准基金资助项目（No.13DZ0500501）

Foundation Items： Key Program of National Natural Science Foundation of China（No.61332019），The National Natural Science Foundation of China（No.61572304，No.61272056），The Technical Standard of Shanghai Science and Technology Innovation Action Plan（No.13DZ0500501）