基于非等距BFA—GM（1，1）模型的尾翼疲劳寿命预测

杨大炼　刘义伦　李松柏　陶洁

摘 要：针对非等距GM（1，1）模型中背景值系数α对模型的预测能力影响很大而最优值难以确定的问题，将细菌觅食算法与GM（1，1）模型相结合，提出了BFA-GM（1，1）优化模型.以飞机尾翼疲劳寿命预测为实例，分析比较了BFA-GM（1，1）模型、PSO-GM（1，1）模型和GA-GM（1，1）模型的性能.从试验的结果来看，本文提出的BFA-GM（1，1）模型消耗的时间少于其他2种模型消耗的时间，而平均预测误差低于其他2种模型的平均预测误差，这说明本文提出的BFA-GM（1，1）模型能够更快速、更准确地找到最优的背景值系数α，从而提高了“小样本”“贫信息”条件下的飞机尾翼疲劳寿命预测的精度.

关键词：细菌觅食算法；非等距GM（1，1）模型；疲劳；寿命预测；参数优化

中图分类号：TG146.2 文献标识码：A

Abstract：The background value coefficient α of the non-equidistant GM （1， 1） model has great influence on the predictive capability， but it is difficult to determine its optimal value. For these problems， the bacterial foraging algorithm and a GM （1， 1） model were combined and the BFA-GM （1， 1） optimization model was proposed. Taking the experiment of empennage fatigue life prediction as an example， the performances of the BFA-GM （1， 1） model， the PSO-GM （1， 1） model and the GA-GM （1， 1） model were analyzed and compared. The results have shown that the BFA-GM （1， 1） model consumes the least time and obtains the lowest average prediction error， and that the BFA-GM （1， 1） model proposed is competent to find the optimal background value coefficient α quickly and accurately， thereby increasing the empennage fatigue life prediction accuracy under the conditions of “small samples” and “poor information”.

Key words：bacterial foraging algorithm （BFA）；non-equidistant GM （1，1） model；fatigue； life prediction； parameter optimization

疲劳是航空航天装备运行不可忽视的问题，对结构寿命进行准确预测能有效避免事故的发生.传统的疲劳寿命预测方法大多建立在确定性理论或者概率统计基础之上[1]，这需要大量而准确的试验数据，从而增加了试验的成本和周期，限制了其应用范围.GM（1，1）模型[2]由于其“小样本”“贫信息”建模的特点被应用于冶金[3]、隧道[4]、军事[5]、疲劳[6-8]等领域.非等距GM（1，1）模型修正了等距GM（1，1）模型要求数据必须是等间隔的局限，是目前研究和应用最多的一种.然而，在使用非等距GM（1，1）模型时，其预测精度受背景值系数α的影响很大[9]，而最优α值难以确定，常凭经验选取，难以保证模型预测能力.为此，王国华等[10]、Hsu[11]采用遗传算法对模型参数进行选取；刘虹，于丽亚等[12-13]采用粒子群算法对模型参数进行选取，但由于遗传算法和粒子群算法本身的局限性，其优化的速度和精度不理想.

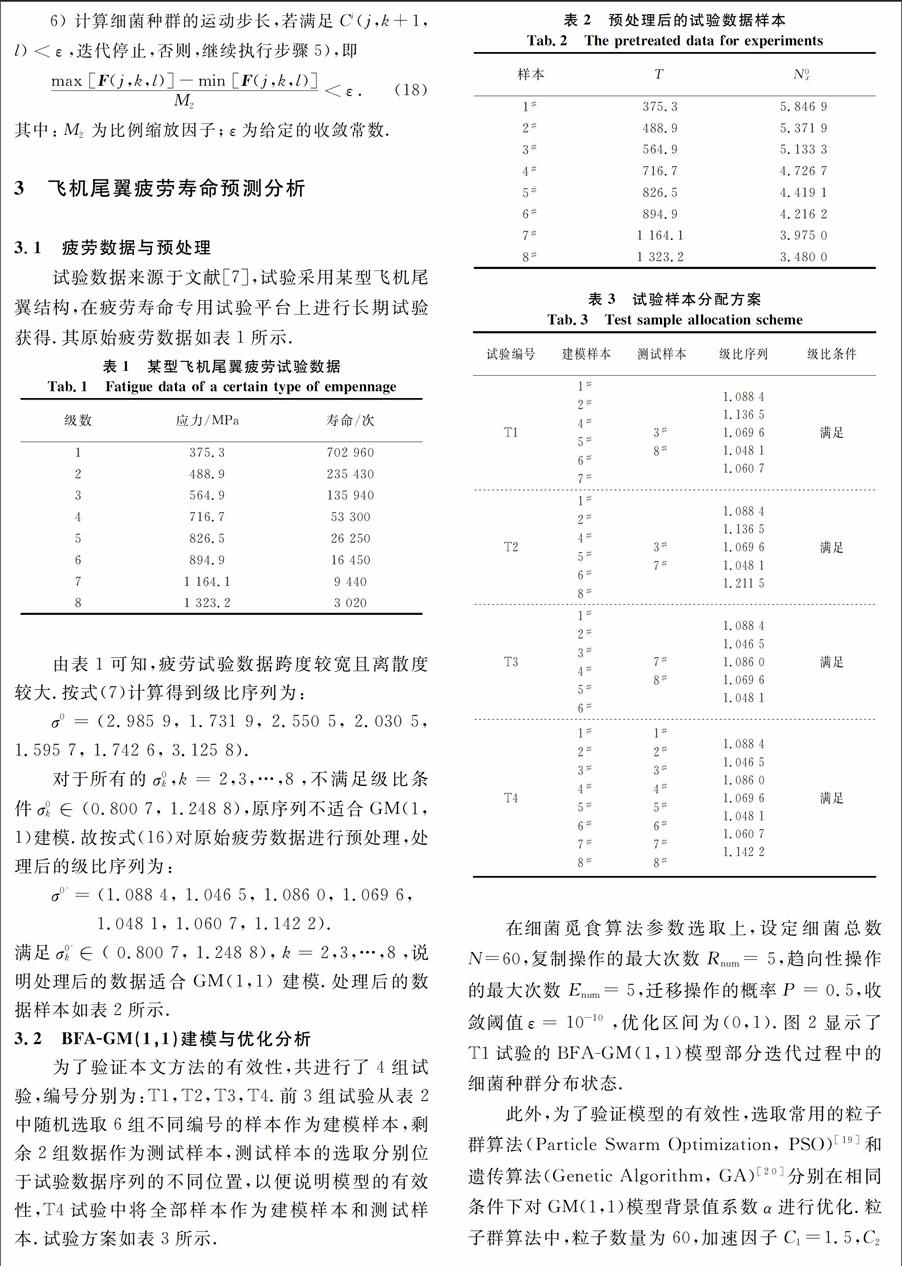
3.2 BFA-GM（1，1）建模与优化分析

为了验证本文方法的有效性，共进行了4组试验，编号分别为：T1，T2，T3，T4.前3组试验从表2中随机选取6组不同编号的样本作为建模样本，剩余2组数据作为测试样本，测试样本的选取分别位于试验数据序列的不同位置，以便说明模型的有效性，T4试验中将全部样本作为建模样本和测试样本.试验方案如表3所示.

比较表4中的4组试验的结果，从终止条件来分析，本文提出的BFA-GM（1，1）模型迭代次数均没有达到设定的最大次数Niter=100就使种群满足ε<10-10，而其他2种模型迭代停止时达到了设定的最大迭代次数，这说明BFA-GM（1，1）模型的收敛速度比后2种模型的收敛速度快.BFA-GM（1，1）模型所需要的时间少于其他2种方法，依次为T1：1.72 s；T2：1.81 s；T3：1.80 s；T4：1.75 s；PSO-GM（1，1）模型消耗的时间次之，而GA-GM（1，1）模型消耗的时间最多，4组试验中最少也需要2.99 s.原因在于粒子群算法中粒子的运动特性受多个参数的共同控制，在实际应用过程中难以对粒子的寻优能力进行最优控制.遗传算法一方面需要对解进行编码及解码操作，而编码的长度直接影响算法的速度和解的精度，编码越长，精度越高，但计算时间就越长，编码短，则精度又无法保证；另一方面，遗传算法需要进行交叉、变异等操作，需要消耗很多的时间，影响了迭代的速度.从表4中的预测误差可以看出，本文提出的BFA-GM（1，1）模型的预测精度比其他2种方法高，依次为8.901 6%，12.868 4%，9.974 9%，8.745 3%，这表明本文提出的BFA-GM（1，1）模型具有优越性.

3.3 尾翼寿命预测结果分析

为了说明参数α对预测结果的影响，试验选取α=α*，α=rand（）和α≠α*时对测试样本及建模样本同时进行预测.表5为BFA-GM（1，1）模型对所有数据样本进行预测并根据式（16）还原为尾翼寿命的预测结果，其中标星号的数据为对应的测试样本的预测结果，其余为建模样本的预测结果.

从表5中4组试验的预测结果可以知道，一方面，背景值系数α对GM（1，1）模型的预测结果影响很大，以T1为例，当α 取优化解α*=0.472 047时，平均误差为8.901 6%，远小于非优化值α=0.147 748时的预测平均误差22.638 4%，这说明对α的值进行优化选取是十分必要的，通过对参数α进行优化选取，能大大降低预测误差；另一方面，对于不同的GM（1，1）模型，其最优背景值α*是不一样的，如果通过随机选取或凭经验选取，无法保证模型的预测精度.

从4组试验的优化预测结果来看，T4的平均误差最小，其次是T1，误差最大为T2，这说明建模样本及预测样本的数量和分布对BFA-GM（1，1）模型的性能有一定的影响.一方面，GM（1，1）模型的性能受建模数据的光滑程度的影响，若建模数据中存在跳跃点，模型的性能会下降；另一方面，样本间距的不均匀性也对模型的性能有一定的影响，从而导致试验中部分点的预测误差偏大，这是今后需要继续深入研究的.但总体来看，平均预测误差分别为8.901 6%，12.868 4%，9.974 9%，8.745 3%是完全可以接受的.

4 结 论

论文将细菌觅食算法与非等距GM（1，1）模型相结合，提出了非等距BFA-GM（1，1）模型，并以飞机尾翼疲劳寿命预测为实例，比较分析了BFA-GM（1，1）、PSO-GM（1，1）和GA-GM（1，1） 3种模型的性能，得出以下结论：

1）在对非等距GM（1，1）模型背景值系数α进行优化时，细菌觅食算法比粒子群算法和遗传算法更适合，前者能够提高优化的速度和模型预测精度.

2）BFA-GM（1，1）优化模型适合对飞机尾翼疲劳寿命进行建模及预测，为寿命预测提供了一种快速、有效的方法.

参考文献

[1] 孙玉兰，王茂廷.基于灰色模型GM（1，1）的疲劳寿命预测[J].科学技术与工程，2011， 11（3）：560-562.

SUN Yu-lan，WANG Mao-ting.Prediction for fatigue life based on grey model GM （1， 1）[J]. Science Technology and Engineering， 2011， 11（3）： 560-562.（In Chinese）

[2] CHEN C I，HUANG S J.The necessary and sufficient condition for GM （1， 1） grey prediction model[J]. Applied Mathematics and Computation，2013， 219（11）： 6152-6162.

[3] 伍铁斌，阳春华，孙备，等. 灰色模糊LSSVM预测模型在锌净化除钴中的应用[J].中国有色金属学报，2012， 22（8）： 2382-2386.

WU Tie-bin，YANG Chun-hua，SUN Bei，et al.Grey fuzzy-LSSVM forecasting model and its application in cobalt removal from zinc electrolyte[J]. The Chinese Journal of Nonferrous Metals， 2012， 22（8）： 2382-2386.（In Chinese）

[4] 郭云开，谢腾，程刚，等.非等时距灰色预测模型在连拱隧道监测中的应用[J]. 现代隧道技术，2013，50（1）： 73-79.

GUO Yun-kai，XIE Teng，CHENG Gang，et al.Application of unequal time-interval grey predicting model to multiple-arch tunnel monitoring [J]. Modern Tunneling Technology， 2013，50（1）：73-79.（In Chinese）

[5] TONG R，SHEN M X，KANG J S，et al.Gray-markov GM（1， 1） prediction model optimal allocation of equipment maintenance personnel based on difference method[J]. Applied Mechanics and Materials， 2014， 484： 847-852.

[6] NI C C.Prediction of fatigue crack growth of 2024-t351 by grey GM （1， 1） model with rolling check [J]. Advanced Materials Research，2013，690：1779-1783.

[7] 崔建国，巩俊杰，董世良，等.基于灰色理论的飞机结构疲劳寿命预测[J].沈阳航空航天大学学报，2011，28（1）：23-27.

CUI Jian-guo，GONG Jun-jie，DONG Shi-liang，et al. Fatigue life prediction of aeroplane structures based on grey theory[J]. Journal of Shenyang Aerospace University， 2011， 28（1）： 23-27.（In Chinese）

[8] 李晓钢，王亚辉.利用非等距灰色理论方法判定失效机理一致性[J].北京航空航天大学学报，2014，40（7）：899-904.

LI Xiao-gang，WANG Ya-hui.Identification method of failure mechanism consistency by non-equidistance grey theory model[J]. Journal of Beijing University of Aeronautics and Astronautics， 2014， 40（7）：899-904.（In Chinese）

[9] 肖新平，毛树华.灰色预测与决策方法[M].北京：科学出版社， 2013： 202-214.

XIAO Xin-ping，MAO Shu-hua.Grey forecasting and decision-making methods[M]. Beijing： Science Press， 2013：202-214.（In Chinese）

[10]王国华，辛江涛，辛敏洁，等.基于遗传算法的GM（1，1，λ）改进模型[J].电子设计工程，2014，22（10）：38-41.

WANG Guo-hua，XIN Jiang-tao，XIN Min-jie，et al. Improved grey model based on genetic algorithm [J]. Electronic Design Engineering， 2014， 22（10）： 38-41.（In Chinese）

[11]HSU L C.Forecasting the output of integrated circuit industry using genetic algorithm based multivariable grey optimization models[J].Expert Systems with Applications，2009， 36（4）：7898-7903.

[12]刘虹， 张岐山.基于微粒群算法的GM（1，1，λ）模型的机械产品寿命预测[J].机械设计，2007，24（10）：4-5.

LIU Hong，ZHANG Qi-shan.Life-span prediction on mechanical products of GM （1， 1， λ） model based on particle swarm algorithm [J]. Journal of Machine Design， 2007， 24（10）： 4-5.（In Chinese）

[13]于丽亚，王丰效.基于粒子群算法的非等距GOM（1，1）模型[J]. 纯粹数学与应用数学， 2011， 27（4）： 472-476.

YU Li-ya，WANG Feng-xiao.Non-equidistant GOM （1， 1） model based on particle swarm optimization algorithm [J]. Pure and Applied Mathematics，2011，27（4）： 472-476.（In Chinese）

[14]BLUM J，DING M，THAELER A，et al. Handbook of combinatorial optimization[M]. New York： Kluwer Academic Publishers， 2004： 329-369.

[15]KEVIN M P.Biomimicry of bacterial foraging for distributed optimization and control[J].IEEE Control Systems Magazine， 2002， 22（3）： 52-67.

[16]DEVABALAJI K R， RAVI K， KOTHARI D P. Optimal location and sizing of capacitor placement in radial distribution system using bacterial foraging optimization algorithm [J]. International Journal of Electrical Power & Energy Systems， 2015， 71： 383-390.

[17]PANDA R， NAIK M K. A novel adaptive crossover bacterial foraging optimization algorithm for linear discriminant analysis based face recognition [J]. Applied Soft Computing， 2015， 30：722-736.

[18]杨大炼， 刘义伦， 李学军， 等. 基于细菌觅食优化决策的齿轮箱故障诊断[J]. 中南大学学报：自然科学版， 2015，46（4）：1224-1230.

YANG Da-lian，LIU Yi-lun，LI Xue-jun，et al.Gearbox fault diagnosis based on bacterial foraging algorithm optimization decisions[J]. Journal of Central South University：Science and Technology，2015，46（4）： 1224-1230.（In Chinese）

[19]曹一家， 曹丽华， 李勇， 等. 改进的自适应多目标粒子群算法[J]. 湖南大学学报：自然科学版， 2014，41（10）：84-90.

CAO Yi-jia，CAO Li-hua，LI Yong，et al.Improved adaptive multiobjective particle swarm algorithm[J]. Journal of Hunan University：Natural Sciences， 2014， 41（10）： 84- 90.（In Chinese）

[20]邓元望， 王兵杰， 张上安， 等. 基于混沌遗传算法的PHEV能量管理策略优化[J]. 湖南大学学报：自然科学版， 2013，40（4）：42-48.

DENG Yuan-wang，WANG Bing-jie，ZHANG Shang-an，et al. Optimization of energy management strategy of PHEV based on chaos-genetic algorithm [J]. Journal of Hunan University：Natural Sciences， 2013， 40（4）：42-48.（In Chinese）