质量时变系统的动载荷识别

彭凡　王樑　肖健

摘 要：研究质量时变系统的动态载荷识别技术，引入广义模态概念，在初瞬时的模态空间中利用模态叠加法得到部分解耦的动力学方程，结合考虑质量变化效应的虚拟变形法和Duhamel积分，构建反演动态力的2种分析途径.一种是基于加速度反演的连锁递推格式，另一种是基于位移和加速度反演的正则化求解格式.分析2个动载荷作用下的变质量多自由度系统，利用Euler中点辛差分方法求得系统的响应，将其叠加随机噪声以模拟测点响应，然后，应用2种模态力反求格式反演动载荷.研究结果表明，连锁递推格式计算效率高，但对加速度测量噪声敏感；正则化求解格式的稳健性较高.

关键词：变质量；动态载荷；反问题；递归计算；正则化

中图分类号：O326；O347.1 文献标识码：A

Abstract：The technique of the load identification of mass variable system was studied. The generalized modal concept applied on time-varying system was introduced， and the method of modal superposition was used to give dynamic equations with partially decoupled in initial modal space defined at initial instant. Based on both virtual distortion method （VDM） accounting for the effect of mass change and the Duhamel integration in initial modal space， two approaches to identify modal forces were constructed： one is the recursive calculation pattern formulated on the basis of modal acceleration， and the other is the regularized solution by the direct discretization of Duhamel integration with modal displacement and acceleration. A mass variable system with 16 degrees of freedom subjected to two external loads was analyzed. The responses were calculated by applying Euler midpoint symplectic difference method and added with random noise to simulate measured signals. Two dynamic loads were identified by two inversion approaches of modal forces. The comparison of results has indicated that regularized solution format has a higher numerical robust than the recursive calculation pattern， but the latter is sensitive to the noise of measurement.

Key words：time-varying mass；dynamic loads；inverse problems； recursive calculation； regularization

许多工程领域存在质量等振动参数随时间发生变化的动力学问题 [1-5].质量时变系统的动力学响应分析方法主要包括2类，一类是直接积分法，包括Newmark法和各类差分算法[6]；另一类是基于短时时不变假设的模态叠加法[7-8].与动力响应分析相对应的是质量时变振动系统的载荷反求，如考虑质量快速减少的运载工具的脉动推力反求，这在工程上也是非常有意义的课题.针对时不变结构的动态载荷识别，已经发展了较为丰富的方法与技术[9].然而，关于时变结构的动态载荷识别方法的研究还较少，张青霞等[10]将车桥系统视为质量时变系统，移动荷载的反求转化为移动质量的识别，基于虚拟变形法识别移动质量.

本文研究质量时变系统载荷识别方法，在初始模态空间中，结合模态叠加和虚拟变形技术，构造模态力反求格式，经模态转换得到相应的物理量.分析变质量多自由度系统，首先由差分法计算受激振动响应，将其叠加噪声以模拟测量信号，然后，反求模态力得到动载荷，比较2种反求格式的有效性及优劣.

1 初始模态空间中的模态力计算格式

1.1 基于初始模态求解时变质量系统的动力学方程

3 结 论

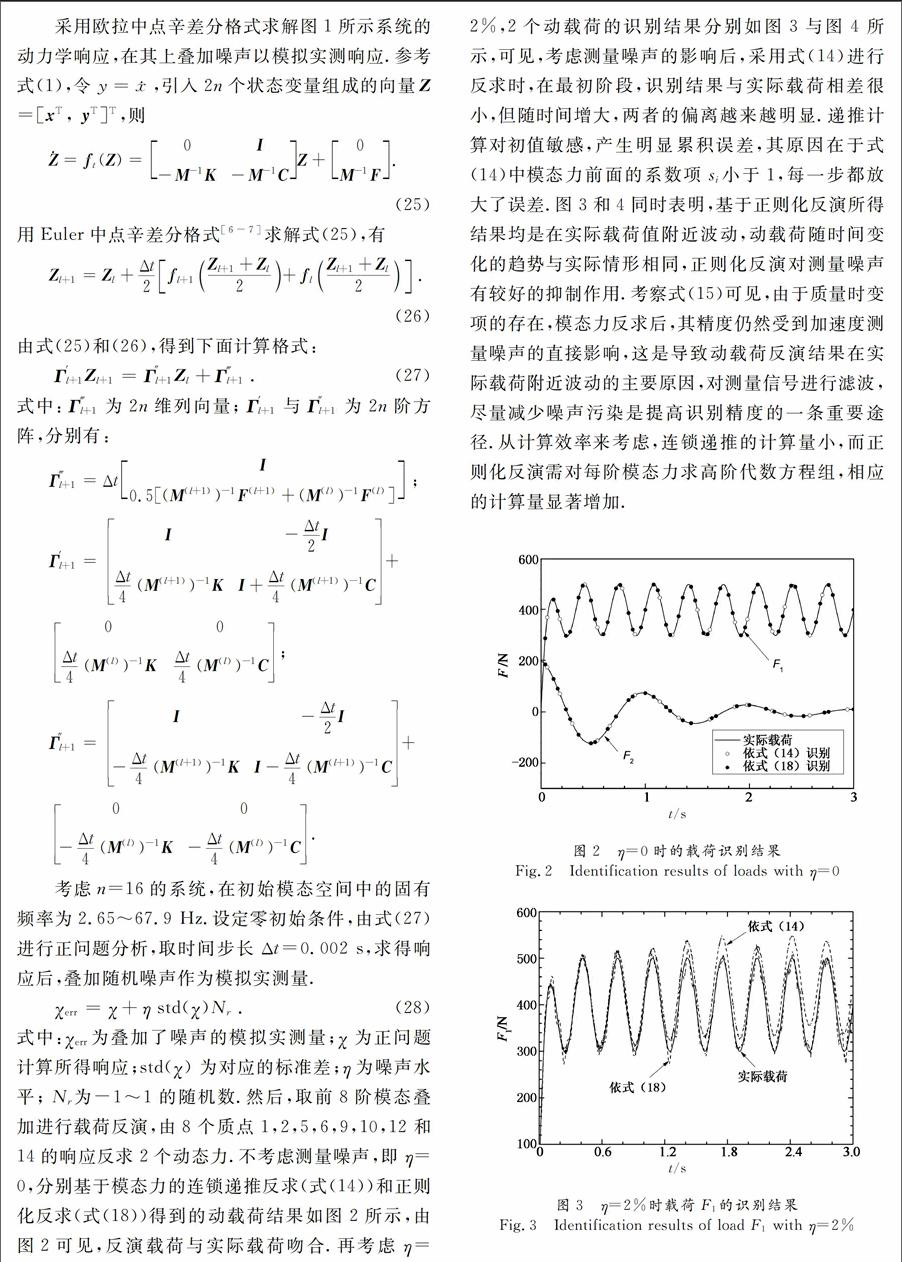
在初始模态空间中建立变质量系统动载荷识别途径.以变质量多自由度系统的动态激励反演为算例，考察所构造的2种模态力反求格式的稳健性和耐噪性.1）利用离散Duhamel积分构造的模态力连锁递推计算仅需加速度测量信号，且计算量小，但容易产生误差累积导致反演结果对初值敏感.2）利用位移的Duhamel积分离散进行模态力的正则化求解格式需要位移、加速度测量信号，稳健性较第1种方法强，计算量较大.

参考文献

[1] JOSHI A. Free vibration characteristics of variable rockets having large axial thrust/acceleration[J].Journal of Sound and Vibration，1995，187（4）：727 -736.

[2] VAN DER BURGH A H P，HARTONO， ABRAMIAN A K. A new model for the study of rain-wind-induced vibrations of a simple oscillator[J].International Journal of Non-Linear Mechanics， 2006， 41（3）： 345-358.

[3] 沈国辉，徐晓斌，楼文娟，等.导线覆冰脱冰有限元模拟方法的适用性分析[J]. 工程力学， 2011， 28（10）：9-15.

SHEN Guo-hui， XU Xiao-bin， LOU Wen-juan，et al.Applicability analysis of finite element methodologies to stimulate the ice-accreting and ice-shedding on transmission lines[J].Engineering Mechanics， 2011， 28（10）：9-15.（In Chinese）

[4] 曹国华，朱真才，彭维红，等.变质量提升系统钢丝绳轴向-扭转耦合振动特性[J]. 振动与冲击， 2010， 29（2）：64-68.

CAO Guo-hua， ZHU Zhen-cai，PENG Wei-hong，et al.Axial-torsion coupling vibration characteristics in elevate system with variable mass[J]. Journal of Vibration and Shock， 2010， 29（2）：64-68. （In Chinese）

[5] 廖剑晖，由小川，吕海波，等.发展时变附加质量方法模拟飞行器出水过程[J]. 工程力学，2012， 29（4）：202-223.

LIAO Jian-hui，YOU Xiao-chuan， LV Hai-bo， et al. Development of a time-varying added mass method in the simulations of the water-exit process of underwater vehicle[J]. Engineering Mechanics， 2012， 29（4）：202-223.（In Chinese）

[6] 邢誉峰，杨蓉.动力学平衡方程的Euler中点辛差分求解格式[J]. 力学学报， 2007， 39（1）： 100-105.

XING Yu-feng，YANG Rong.Application of Euler midpoint symplectic integration method for the solution of dynamic equilibrium equations[J]. Chinese Journal of Theoretical and Applied Mechanics， 2007， 39（1）： 100-105.（In Chinese）

[7] 邢誉峰，谢珂，潘忠文.变质量系统振动分析的两种方法[J]. 北京航空航天大学学报，2013， 39（7）：858-862.

XING Yu-feng， XIE Ke， PAN Zhong-wen.Two methods for vibration analysis of variable-mass systems[J]. Journal of Beijing University of Aeronautics and Astronautics， 2013， 39（7）：858-862.（In Chinese）

[8] 于开平， 庞世伟， 赵婕. 时变线性/非线性结构参数识别及系统辨识方法研究进展[J]. 科学通报， 2009，54（20）：3147-3156.

YU Kai-ping， PANG Shi-wei， ZHAO Jie. Advances in method of time-varying linear/nonlinear structural system identification and parameter estimate[J]. Chinese Science Bulletin， 2009， 54（20）： 3147-3156.（In Chinese）

[9] SANCHEZ J， BENAROYA H . Review of force reconstruction techniques[J]. Journal of Sound and Vibration， 2014，333（14）：2999-3018.

[10]张青霞，段忠东，JANKOWSK L.基于虚拟变形法的车-桥耦合系统移动质量识别[J].力学学报， 2011， 43（3）：598-610.

ZHANG Qing-xia， DUAN Zhong-dong， JANKOWSK L. Moving mass identification of vehicle-bridge coupled system based on virtual distortion method[J]. Chinese Journal of Theoretical and Applied Mechanics， 2011， 43 （3）： 598-610.（In Chinese）

[11]KOLAKOWSKI P，WIKLO M， HOLNICKI-SZULC J. The virtual distortion method—a versatile reanalysis tool for structures and systems[J]. Structural and Multidisciplinary Optimization， 2008， 36（2）：217-234.

[12]HANSEN P C.Truncated SVD solutions to discrete ill-posed problems with ill-determined numerical rank[J]. SIAM Journal on Scientific and Statistical Computing，1990，11（3）：503-518.

[13]GOLUB G H， HEATH M， WAHBA G. Generalized cross-validation as a method for choosing a good ridge parameter[J].Technometrics， 1979，21（2）：215-223.