西北太平洋浪流相互作用对有效波高的影响研究
2016-09-28刘娜李本霞王辉吕洪刚
刘娜,李本霞,王辉,吕洪刚
(1. 国家海洋环境预报中心 国家海洋局海洋灾害预报技术研究重点实验室,北京 100081)
西北太平洋浪流相互作用对有效波高的影响研究
刘娜1,李本霞1,王辉1,吕洪刚1
(1. 国家海洋环境预报中心 国家海洋局海洋灾害预报技术研究重点实验室,北京 100081)
西北太平洋强流区会对海浪的特征和分布产生显著的影响,尤其是研究台风过程中海流与海浪的相互作用具有重要的研究意义。本文以ROMS海洋模式和SWAN海浪模式为基础,构建了浪流耦合模式系统,对2013年10月6-17日间的台风“丹娜丝”、“百合”、“韦帕”过程中西北太平洋浪流相互作用中海流对有效波高的影响进行了研究。通过对比模式模拟有效波高与浮标观测资料,发现耦合后的有效波高比非耦合结果更接近观测值,耦合模式中海流的存在对有效波高的分布有明显的影响。研究表明,特别是在有效波高峰值处,海流引起的有效波高增大最大可达1 m。海浪浪向及流向的空间分布以及中国近海浮标处浪向与流向的时间序列表明,流向与浪向反向时,海流的影响造成有效波高增大;二者同向时,有效波高减小。海流对有效波高的调整会沿着海浪传播的方向传播相当一段距离。在西北太平洋的海浪场计算中,引入海流的耦合模式计算结果对改善强流区海浪预报具有重要意义,并且海流的模拟精度对于高精度的海浪预报非常重要。
浪流相互作用;有效波高;台风;西北太平洋
1 引言
早在20世纪60年代Longuet-Higgin和Stewart[1]就提出浪流相互作用的概念。当随机的或沿某个方向的海浪传播遇到随时空变化的海流时,会发生强烈的动量和能量交换,由水平剪切流造成的海浪折射等物理过程会显著影响波向、波长和波能量[2—3],进而调整海浪的有效波高或平均波向等统计特征的分布[4]。
来自船舶和卫星的观测表明,当海浪传播到湾流等西边界流海域时,由于海流造成的复杂海洋状态,使海浪比传入时变得更大[5]。同样的,采用高度计数据研究表明,在太平洋的黑潮区,风场和海浪的分布沿着黑潮主轴会出现局部加强,海流会对海浪的特征产生显著的影响[6—7]。在强流区附近由浪流相互作用造成的波高局部增大甚至波高极大的畸形波也在其他强流区被反复观测到[8—12]。因此,精确估计海流对海浪以及浪流相互作用的影响,对海浪的后报和预报都有着重要的意义。
在实际海洋条件下,需要考虑海浪的非线性、多方向性和海浪的成长和衰减等物理特征和过程。西北太平洋是全球热带气旋活动最活跃的海域,每年发生的热带气旋的次数约占全球的1/3,台风引起的大浪对海上活动有重要的影响,研究西北太平洋台风过程中海流与海浪的相互作用具有重要的意义。为了深入理解海浪经过强流区时的动力机理和特征,国内外学者采用浪流耦合数值模式,充分考虑海浪和海流耦合的影响,对浪流相互作用开展了研究[13—16]。Guan等[17]利用改进的WAM模式通过考虑谱输运方程中辐射应力,研究海流对波浪的影响。本文基于ROMS海洋模式和SWAN海浪模式建立三维浪流耦合数值模型,模拟研究西北太平洋台风过程中海浪经过强流区的有效波高的时空变化特征,并对海流对海浪影响的过程进行讨论和分析。
2 模式介绍及实验设置
2.1模式介绍
本文采用浪流耦合模型研究西北太平洋浪流相互作用对海浪的影响,基于海流模式Regional Ocean Model System(ROMS)和海浪模式Simulation Wave Nearshore(SWAN)而建立三维耦合数值模型。ROMS和SWAN通过Model Coupling Toolkit(MCT)模型耦合软件实现双向耦合,更好地模拟浪流的相互作用。
ROMS模式是由美国Rutgers大学和加利福尼亚大学(UCLA)共同开发的区域海洋模式,在海洋研究领域得到广泛的应用。该模式基于三维非线性斜压原始方程,在垂向静压近似和Boussinesq假定下,按照有限差分近似求解具有自由表面的Reynolds平均原始Navier-Stokes方程[18—19]。水平方向使用正交曲线(Arakawa C)网格,垂直方向采用跟随地形可伸缩的S坐标系统。ROMS模式功能完善,除水动力模块外,还包括海冰模块、生态模块、沉积模块和数据同化模块以及伴随模式,模式为对流方案、边界条件、湍封闭混合方案等提供了多种不同的数值计算方案。在时间上采用内、外模态分离的计算方案, 对内、外模独立求解, 使模式能高效率运行。
SWAN海浪模式是基于波作用平衡方程的第三代海浪数值模型,由荷兰Delft大学开发,主要是为计算浅水与近岸的海浪而设计的,适用于从陆架海到破碎带的风浪、涌浪以及混合浪的模拟。SWAN模式源项的处理应用当今海浪研究最新成果,包括风能输入的线性增长和指数增长、冠破碎引起的能量耗散、底摩擦耗散、海浪深度诱导破碎和非线性相互作用机理,尤其在非线性项中加入三相波相互作用项,能合理模拟近岸海浪传播的周期变化[20],而且将随机海浪以不规定谱型的方向谱表示,更接近真实海浪。
ROMS-SWAN浪流耦合模式系统采用MCT耦合器在模式成员之间高效地传递和转换各种数据[21—22]。MCT耦合器通过并行耦合方式实现子模式间各种变量的传递、转换、再分配以及网格间插值等功能,应用接口程序实现子模式之间协调运行,通过提供灵活的场变量存储数据格式,将两个模式简易快捷地耦合起来[23]。MCT提供协议来为各个模型分配CPU,通过MCT耦合器,ROMS和SWAN模型能够在规定的时间步交换数据。在本文的研究中,ROMS海洋模式将海表面流场、自由海面起伏等变量传递给SWAN模式,SWAN模式向ROMS模式提供有效波高、波长、海浪传播方向、平均波周期、波破碎率等变量。SWAN海浪模式与ROMS海洋模式采用相同的地形。
2.2实验设置
本文中浪流耦合模式系统的模拟区域为10°~50°N,110°~155°E,包括中国东部海域及西北太平洋海域。海洋模式ROMS模式的水平网格分辨率为(1/8)°,垂直方向分为40层。水深数据由分辨率为2′×2′的ETOPO2数据插值到模型的网格上,最小水深为10 m,最大为10 654 m(图1)。ROMS模式中选择垂向拉伸参数,使得Sigma坐标第一层不深于10 m。模式的东、南、西、北4个边界均设为开边界。模式采用来自美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)的全球预报模式(Global Forecast Model,GFS)的逐6小时的0.5°NCEP分析场数据(Final Analysis,FNL)作为大气强迫场,采用来自Climate Forecast System Reanalysis(CFSR)的流场、垂向平均的流场、水位、盐度和温度场作为初始条件,流场、盐度和温度等数据作为侧边界条件。本研究中没有考虑河流径流。开边界采用正压流的Flather开边界条件[24],使风生海流和潮汐可以自由传播。耦合模式系统中SWAN模式与ROMS模式采用相同的水平网格,同样采用FNL分析场数据作为大气强迫场。SWAN模式中风能量输入的指数增长形式采用Komen形式,同时考虑白浪耗散、水深诱导的海浪破碎、底摩擦耗散和波-波非线性相互作用等物理过程。SWAN模式初始状态由静止状态冷启动,考虑到在西北太平洋海域由侧边界传入的涌浪较小,假定开边界不向计算区域传递海浪,将模式侧边界条件均设置为0。在本文实验中,ROMS模式采用300 s斜压时间步长,SWAN模式同样采用300 s时间步长,模式间每3 600 s交换一次数据。
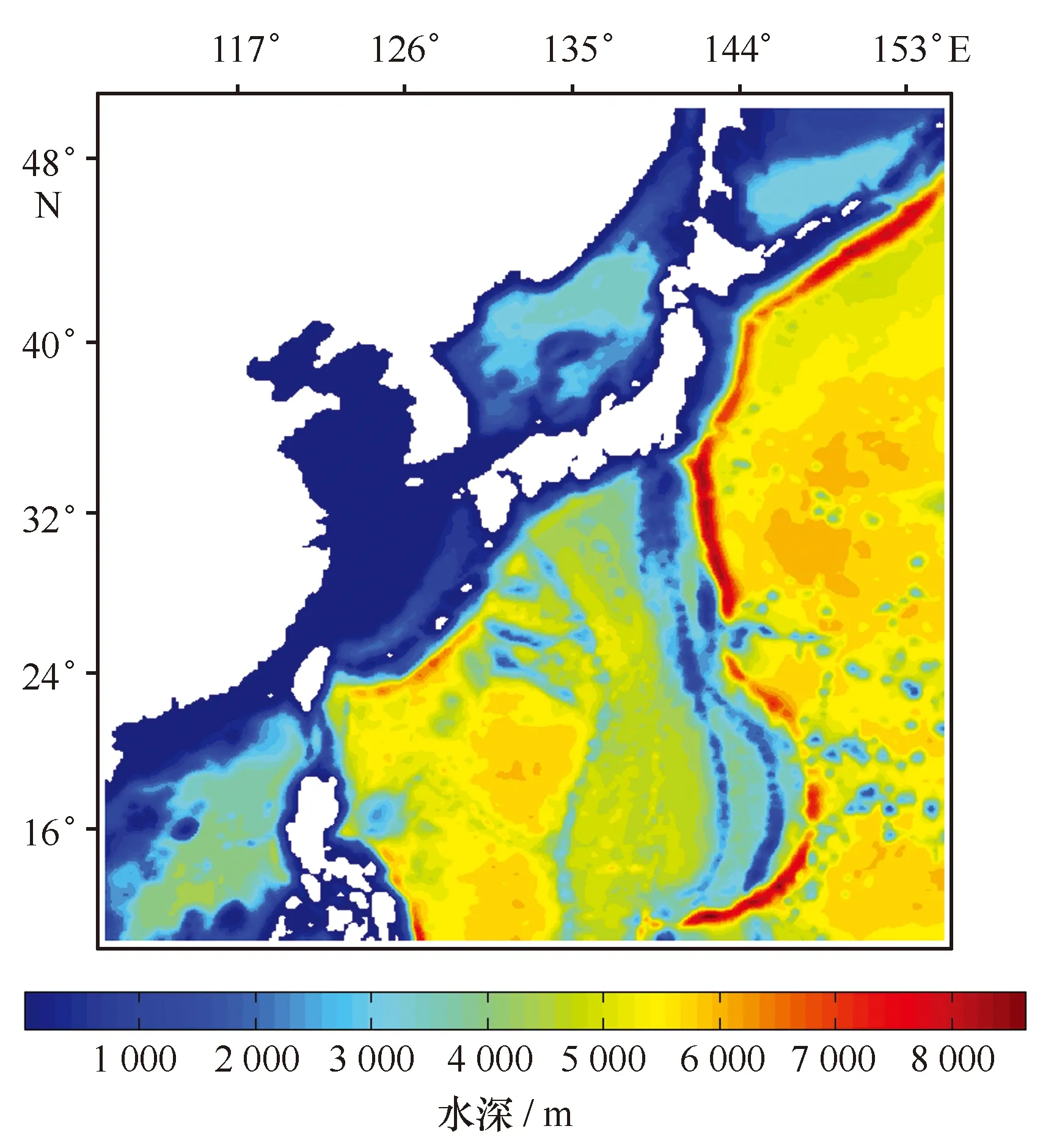
图1 模式计算区域及ROMS海洋模式地形Fig.1 Model domain and the bathymetry in ocean model ROMS
为研究台风过境时西北太平洋浪流之间的相互作用,本文选取2013年10月6—17日时间段进行模拟实验。由于SWAN模式由静止状态冷启动,开始的一段时间内的海浪计算结果不是真实状态,特别是在波高较大的情况下,模拟结果可能会失真,本文采用1 d以后的模拟结果,即将10月7-17日计算结果进行对比研究。在此期间,台风“丹娜丝”、“百合”、“韦帕”3个台风个例经过计算区域。1324号台风“丹娜丝”于2013年10月4日下午在西北太平洋洋面上生成,沿着北偏西方向移动。7日上午8时加强为超强台风,中心附近最大风力达到52 m/s,中心最低气压为935 hPa,7日下午进入我国东部海域,并先后沿偏北转东北方向移动。10月8日晚上离开东海海域,进入朝鲜海峡,9日强度减弱为热带风暴,并停止编号。1325号台风“百合”于2013年10月8日在西北太平洋洋面生成,然后主要沿着西偏北路径移动,10月11日23时左右登陆菲律宾后,进入南海东部海面,然后继续沿着偏西方向移动,中心最低气压为960 hPa,中心附近最大风速达到40 m/s,10日15时凌晨左右在越南中部地区登陆。1326号台风“韦帕”于2013年10月11日凌晨2时在西北太平洋洋面上生成,然后沿西北转向西北偏北方向移动,强度逐渐加强到强台风,10月15日上午8时在西北太平洋洋面减弱为台风,沿北偏东逐渐转向东北方向快速移动,强度逐渐减弱,10月16日14时对其停止编号。台风“丹娜丝”、“百合”、“韦帕”的路径见图2。本文通过台风“丹娜丝”、“百合”、“韦帕”3个台风过境期间耦合与非耦合对比实验研究台风海况下海流对海浪有效波高的影响。
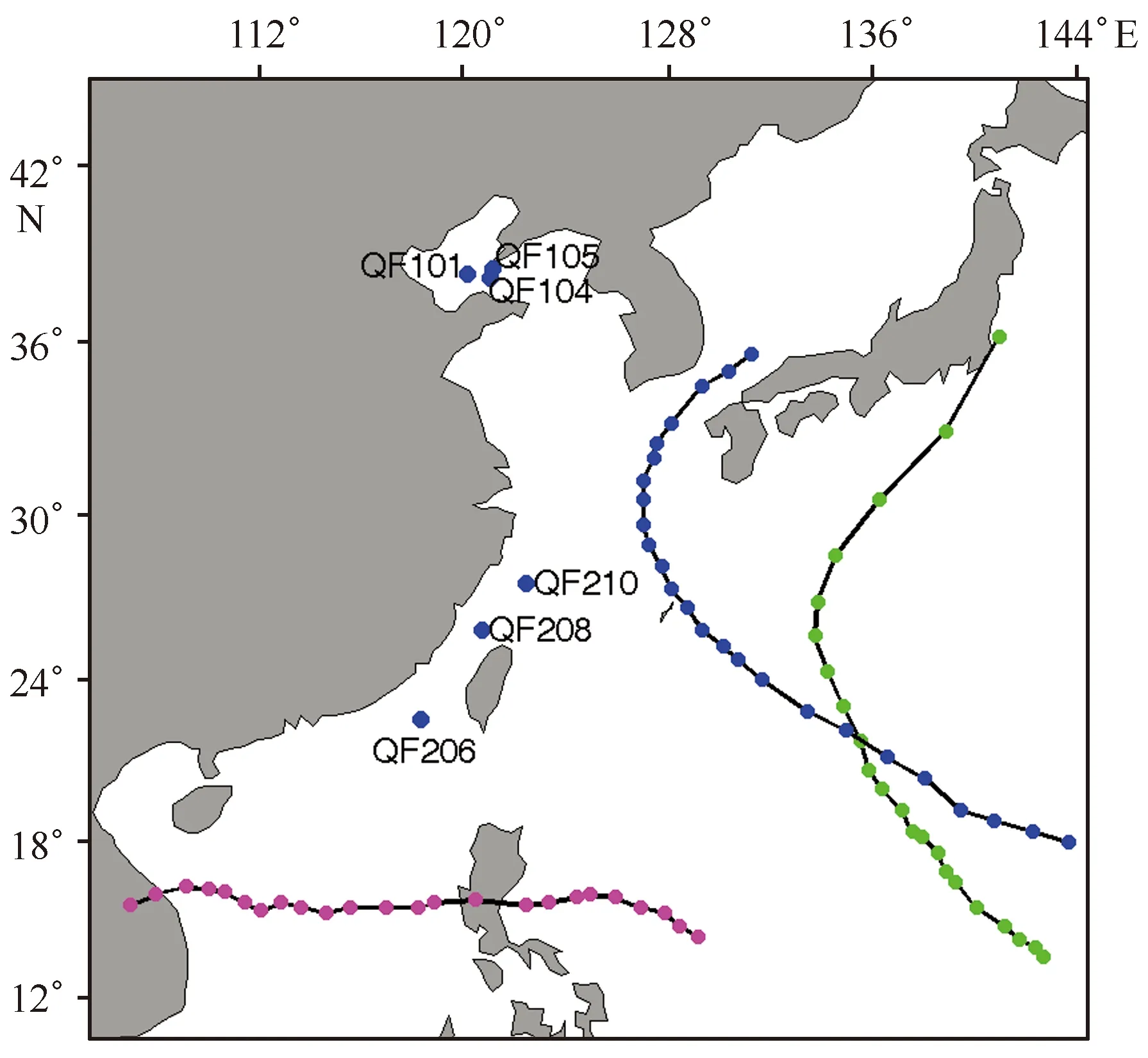
图2 台风“丹娜丝”(蓝线)、“百合”(紫线)、“韦帕”(绿线)路径及中国近海浮标位置(蓝点)Fig.2 Typhoon path for Typhoon Danas (blue line), Typhoon Nari (purple line), Typhoon Wipha (green line), and location of buoys in China coastal area (blue dot)
3 模拟结果验证
为了考察浪流相互作用对海浪模拟的影响,本文通过浪流耦合模式系统设计了耦合与非耦合两组模拟实验,对比研究海流对有效波高的影响。(1)ROMS-SWAN:耦合系统中ROMS与SWAN耦合;(2)SWAN:只采用SWAN模式模拟海浪,不包括海流对海浪的反馈作用。
3.1浮标对比
选取位于中国近海的QF101、QF104、QF105、QF206、QF208、QF210六个浮标,浮标所在位置如图2所示。将2013年10月6-17日两组对比实验中模拟的有效波高与中国近海浮标观测的有效波高进行对比(图3)。从图中可以看出,QF101、QF104、QF105浮标处的有效波高在10月8日、11日、15日出现有效波高波峰,分别对应台风“丹娜丝”、“百合”、“韦帕”经过时出现的有效波高大值分布,传播到浮标处引起的有效波高显著增大。其中浮标QF101处(图3a)两组实验模拟的有效波高与观测的振幅和时间变化均一致,没有明显的差别。浮标QF104、105处(图3b,3c),在10月10-12日期间,流场的存在影响到波动振幅的计算,耦合模式ROMS-SWAN模拟的有效波高要高于非耦合的SWAN模拟结果,有效波高最大增幅达到1 m左右,更接近于观测结果,显著的提高计算精度。而浮标QF206、208、210处(图3d-f)耦合模式ROMS-SWAN模拟的有效波高要明显低于非耦合的SWAN模拟结果,流场的作用使得模拟结果更接近于观测结果。在浮标QF206、208、210处,海流调整引起有效波高减小,减小值最大可达0.5 m。与以往浪流相互作用的研究结果[16,25]类似,本文研究显示海流对西北太平洋海浪的影响显著,考虑了流的影响后波高计算值与实测值吻合得较好,海流引起有效波高的增大或减小,比较显著的提高有效波高计算精度。通过对比表1中耦合模式与非耦合模式模拟有效波高的平均误差值可见,在大部分浮标处,耦合模式中海流的作用减小了对有效波高的模拟误差,提高有效波高计算精度。

图3 中国近海各浮标处观测(蓝线)及耦合模式ROMS-SWAN(黑线)、非耦合模式SWAN(红线)模拟的有效波高时间序列对比Fig.3 Comparison of observed (blue line) and simulated significant wave height in ROMS-SWAN model (black line), SWAN model (red line) in the location of coastal buoys

表1 耦合模式与非耦合模式模拟有效波高的平均误差
在浪流相互作用中,海流对波浪周期和波向也有非常重要的影响。图4比较了两组数值实验模拟的波浪周期和浮标测量的波浪周期。由图可见,浮标QF101, QF104,QF105观测的波浪周期与数值实验模拟的波浪周期大小较为一致,而浮标QF206,QF208,QF210处观测的波浪周期明显小于数值模拟的波浪周期。图4d-f中可见,耦合模式ROMS-SWAN模拟的波浪周期要小于非耦合的SWAN模拟结果,更接近于观测结果,显著的提高对波周期的计算精度。在浮标QF104、QF105处,在某些时刻耦合模式ROMS-SWAN模拟的波浪周期要明显高于非耦合的SWAN模拟结果,表明是海流引起的波周期的差异。海流对波周期的影响不仅取决于海流的大小,同时也受到波浪参数的影响。图5为两组数值实验模拟的波向与浮标测量的波向的比较。由图可见,观测的波向与数值实验模拟的波向大小较为一致,海流对波向的模拟影响较小。
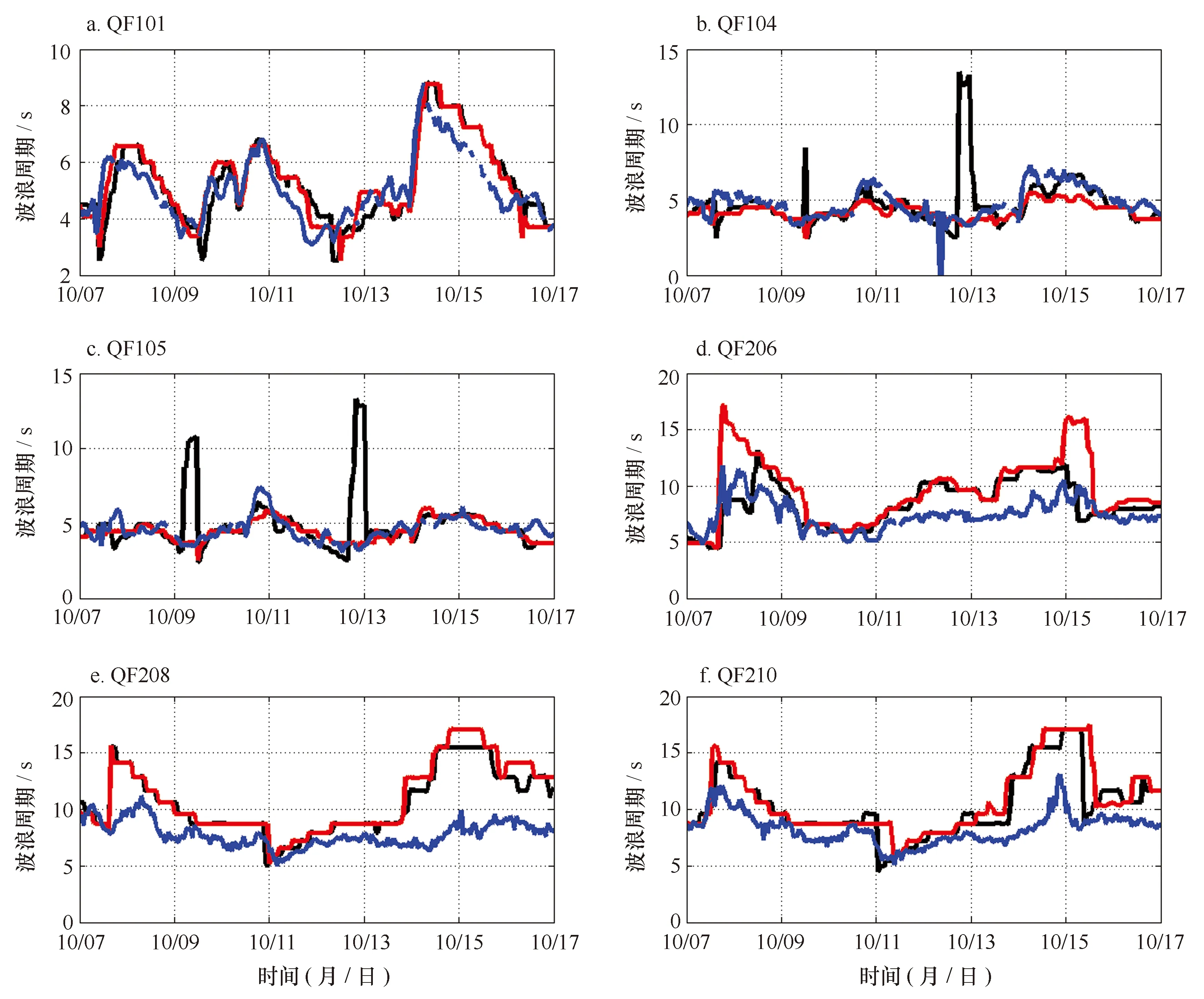
图4 中国近海各浮标处观测(蓝线)及耦合模式ROMS-SWAN(黑线)、非耦合模式SWAN(红线)模拟的波浪周期时间序列对比Fig.4 Comparison of observed (blue line) and simulated wave period in ROMS-SWAN model (black line), SWAN model (red line) in the location of coastal buoys

图5 中国近海各浮标处观测(蓝线)及耦合模式ROMS-SWAN(黑线)、非耦合模式SWAN(红线)模拟的波向时间序列对比Fig.5 Comparison of observed (blue line) and simulated wave direction in ROMS-SWAN model (black line),SWAN model (red line) in the location of coastal buoys
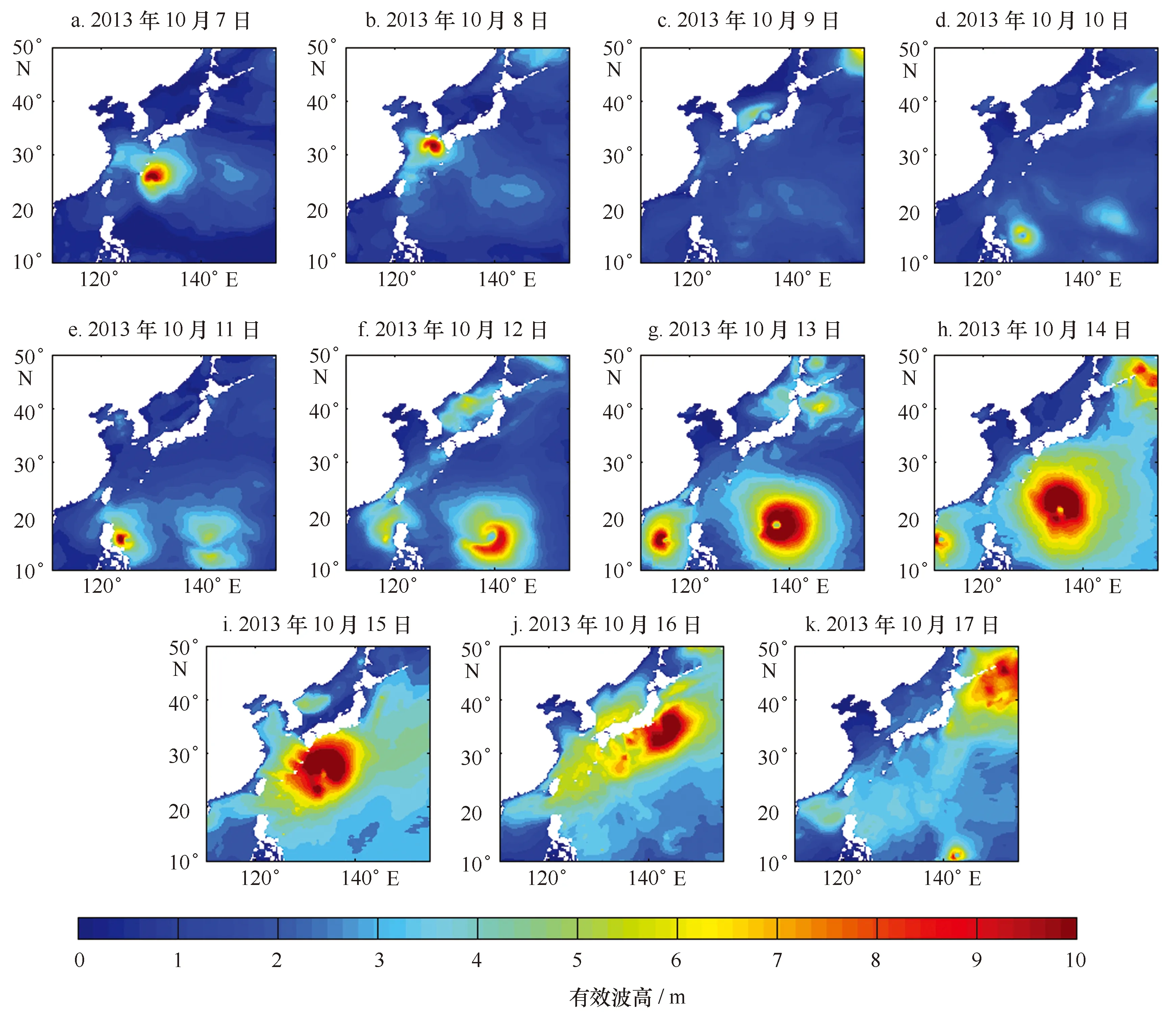
图6 10月7-17日00时耦合模式模拟的有效波高空间分布Fig.6 Spatial distribution of the significant wave height computed in coupled model from October 7 to 17 at 00 hour
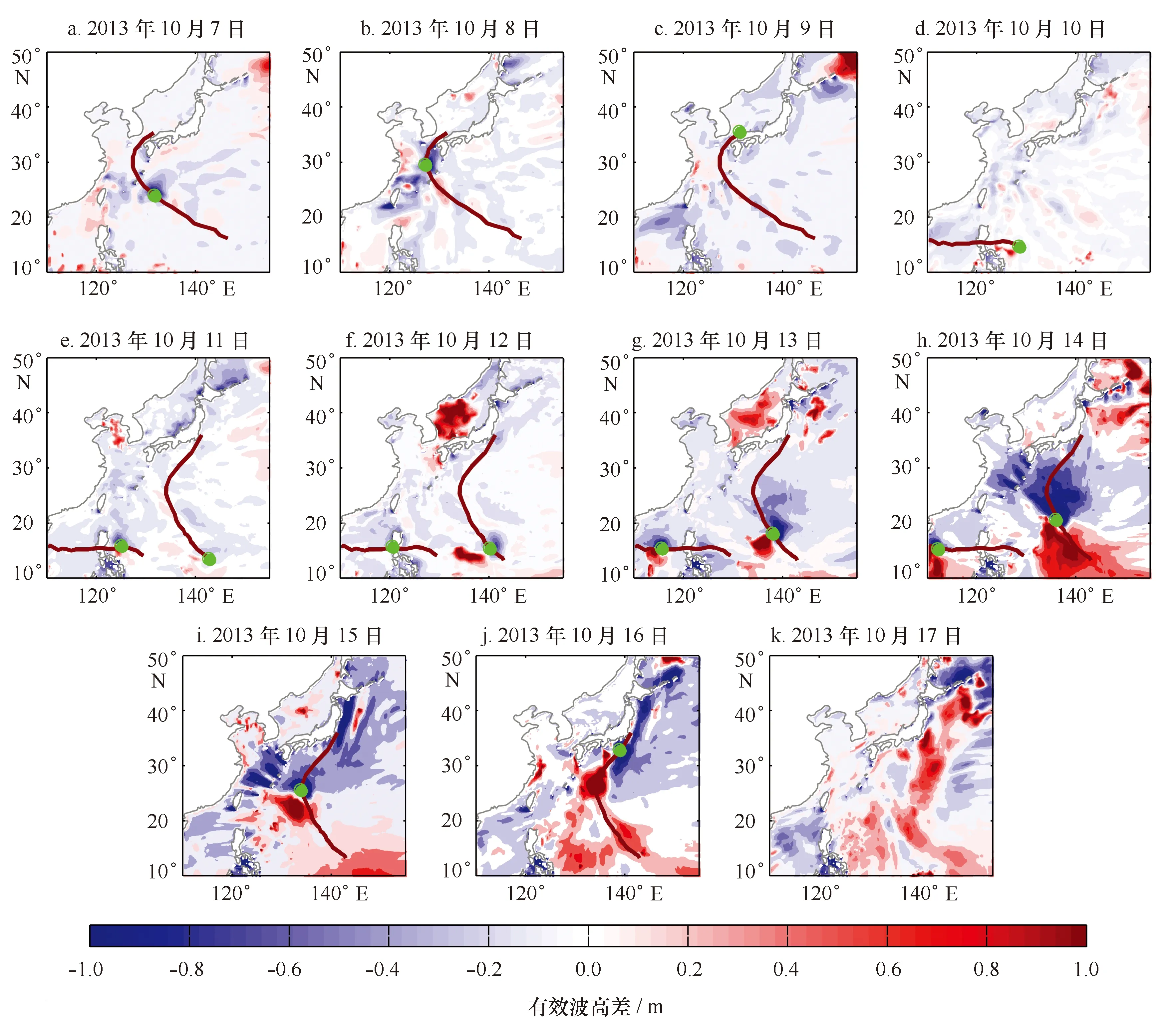
图7 10月7-17日00时耦合模式与非耦合模式模拟的有效波高差值的空间分布,以及台风路径(红线)和台风中心位置(绿点)Fig.7 Differences of simulated significant wave height between coupled model and uncoupled model from October 7 to 17 at 00 hour. Typhoon paths (red line) and center position of typhoon (green dot) are superimposed
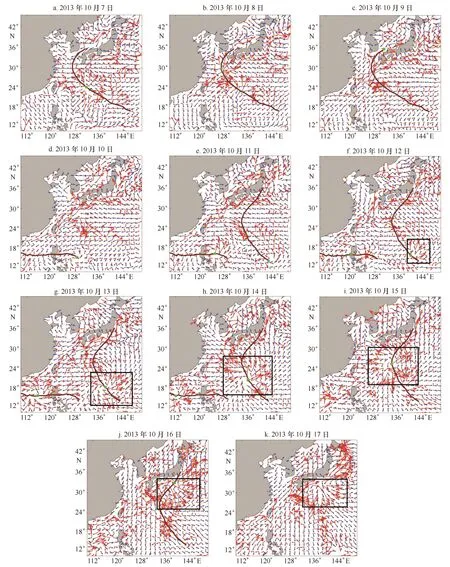
图8 10月7-17日00时耦合模式模拟的海流场(红色箭头)与浪向场(蓝色箭头)的空间分布及台风路径(红线)和台风中心位置(绿点),黑色方框为台风附近较强海流区域Fig.8 Spatial distribution of simulated ocean current field (red vector) and wave field (blue vector) in coupled model from October 7 to 17 at 00 hour. Typhoon paths (red line) and center position of typhoon (green dot) are superimposed, black rectangle is the area of strong ocean current near typhoon
3.2有效波高分布
台风经过海洋时的一个直接作用,会将能量和动量从大气传递到海洋。图6为ROMS-SWAN耦合模式模拟的10月7日00时至17日00时刻整个计算区域的有效波高分布情况。可以看出,台风经过的海域会出现有效波高的大值区,图中显示了台风“丹娜丝”、“百合”、“韦帕”发展和减弱的过程。10月7-8日为台风“丹娜丝”经过时产生有效波高大值区,中心附近最大有效波高达到10 m,10月10-14日南海附近有效波高大值区为台风“百合”过境时产生,中心附近最大有效波高达到12 m,10月11-17日西北太平洋出现的有效波高大值区,由台风“韦帕”过境时引起,中心附近最大有效波高超过15 m。
4 海流对海浪影响分析
为了更好地理解浪流相互作用对海浪的作用机理,接下来进一步分析海流在调整有效波高中的作用,研究台风海况下,海流引起的海浪特征的变化。图7所示为ROMS-SWAN耦合系统模拟的海浪方向分布,以及耦合与非耦合的情况下模拟的有效波高之差。图8所示为海浪浪向场与海流流场的空间分布,台风经过时引起的较强海流区域由黑色方框标出。由图7中可见,在台风的局地强风作用下,海流的影响引起了有效波高的加强或减弱。台风附近有效波高的调整源于台风中心,并且在沿着海流较强的区域(见图8中黑色方框的标注区域),有效波高产生明显的变化。由海流影响引起的有效波高之差的最大值出现在10月14日,在台风东南侧海域,最大的有效波高增加超过1 m,台风西北侧海域有效波高减小。浪流相互作用的影响不仅是局地,会随台风的移动而传播,在考虑了海流影响后的有效波高的差值从台风中心沿着海浪传播的方向传播相当一段距离(图7f-k)。从文中分析可以得出,耦合模式中表层海流对海浪有显著的影响,浪流相互作用对海流结构非常敏感。
由海浪浪向分布图(图8)可见,在围绕台风中心的旋转风场作用下,台风经过的海域也形成相应的逆时针旋转海浪场。同样的,在台风的旋转风场作用下,流场也反映出与台风相对应的旋转特性,漩涡中心处流速较小,四周流速呈现旋转外扩分布,且流速较大。从表层流场分布看出,在中国近海海域,台风过境时海洋表层呈现较明显的沿岸流现象,黑潮从台湾以东进入东海,主轴沿大陆架边缘向东北流动,经吐噶喇海峡流出东海,流速一般在0.5 m/s以上,最大可达1 m/s。
结合图7和图8综合分析可以看出,在台风周围的北部海域,海浪沿着海流的方向传播或与流向之间的夹角较小(小于90°),海浪被折射回来,不能穿越海流[11],造成有效波高减小。而在台风的南部海域,海浪浪向与流向反向,或夹角大于90°时,会造成有效波高增大。这一结果与以往研究[6,16]的结果一致。此外,分析可得,浪流相互作用对海浪的影响主要分布于流速较大的海域,因此,当流速越大时,由浪流相互作用引起的有效波高的调整越大,这与Hwang[6]得出的海流引起的有效波高的增大或减小线性正比于海流流速定性上是一致的。
为了进一步研究中国近海6个浮标处,耦合模式中海流对有效波高的调整作用,分析浮标处流向与浪向的关系。图9所示为选取的6个浮标位置处,耦合模式系统模拟的海浪浪向和海流流向变化的时间序列。图9a-c中可见流向的变化为半日周期,原因是流向主要受当地半日潮周期的影响,而在该段时间内波向受台风风场影响,呈现出逆时针旋转,在模拟时段内该海区流向与波向表现出不同的变化周期。可见流向的变化为半日周期,原因是在该段时间内波向受台风风场影响,呈现出逆时针旋转,而流向主要受当地半日潮周期的影响,在模拟时段内该海区主要是流向的变化造成了有效波高的变化。图9d-f中可见,海浪方向基本保持不变。通过对比图3与图9分析发现,在浮标QF101、QF104、QF105处,在10月8日、11日、15日之前出现流向与浪向相反,造成有效波高增大;而浮标QF206、208、210处当流向与浪向基本保持同向或夹角小于90°,有效波高减小。这一结果与图8中所示浪向与流向的夹角对有效波高的影响关系类似,当海浪方向与背景海流方向反向时,耦合后有效波高增大;二者同向时,耦合后有效波高减小。浪流相互作用对海浪的影响主要分布于流速较大的海域,SWAN计算时,流的影响比较显著,在考虑流的影响后,能有效地减小计算误差。
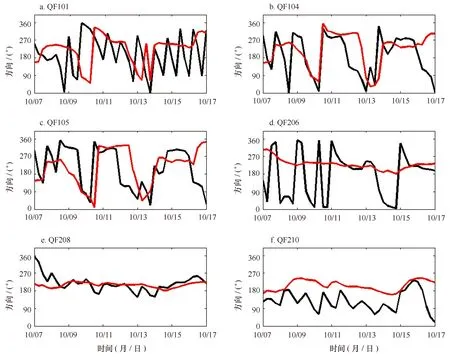
图9 耦合模式模拟的流向(黑线)、浪向(红线)时间变化序列Fig.9 Time series of simulated current direction (black line) and wave direction (red line) in coupled model
5 结论
为了更好的理解台风过程中海浪经过强流区时海流引起的有效波高的调整,以及浪流相互作用的动力机理和特征,本文采用基于ROMS海洋模式和SWAN海浪模式建立三维浪流耦合数值模型,研究海流对台风过程中海浪经过强流区的有效波高的时空变化特征的影响。
通过耦合与非耦合模式模拟得到的有效波高与浮标实测资料的对比验证表明,浪流相互作用明显的区域集中在海流较大的海域,流场会显著地影响有效波高的分布,耦合模式计算的有效波高与观测值更为接近。海流引起的有效波高增大最大可达1 m。海浪浪向及流向的空间分布表明,在台风周围的北部海域,海浪浪向沿着海流的方向传播或与流向之间的夹角较小,从而造成有效波高减小。而在台风的南部海域,海浪浪向与流向反向,或夹角大于90°时,会造成有效波高增大。海流对有效波高的调整会沿着海浪传播的方向传播相当一段距离。同样的,中国近海浮标处浪向与流向的时间序列表明,流向与浪向反向或同向时,造成有效波高增大或减小。由此可见,浪流相互作用是引起海流加强的一个重要原因,考虑了海流的影响后有助于提高海浪的模拟精度。说明了在西北太平洋的海浪场计算中,引入海流的影响是必要的,对提高海浪预报和后报的精度具有重要意义。
[1]Longuet-Higgins M S, Stewart R W. Radiation stress and mass transport in gravity waves, with application to ‘surf-beats’[J]. Journal of Fluid Mechanics, 1962,13(4): 529-549.
[2]Holthuijsen L H, Tolman H L. Effects of the Gulf Stream in ocean waves[J]. Journal of Geophysical Research, 1991, 96(C7): 12755-12771.
[3]Kenyon K E. Wave refraction in ocean currents[J]. Deep-Sea Research, 1971, 18(10): 1023-1033.
[4]Tamura H, Waseda T, Miyazawa Y, et al. Current-induced modulation of the ocean wave spectrum and the role of nonlinear energy transfer[J]. Journal of Physical Oceanography, 2008, 38(12): 2662-2684.
[5]Mapp G R, Welch C S, Munday J C. Wave refraction by warm core rings[J]. Journal of Geophysical Research, 1985, 90(C4): 7153-7162.
[6]Hwang P A. Altimeter measurements of wind and wave modulation by the Kuroshio in the Yellow and East China Seas[J]. Journal of Oceanography, 2005, 61(5): 987-993.
[7]Hwang P A, Teague W J, Jacobs G A. Spaceborne measurements of Kuroshio modulation of wind and wave properties in the Yellow and East China Seas[J]. J Adv Mar Sc and Tech Soc, 1998,4(2): 155-164.
[8]Lavrenov I. The wave energy concentration at the Agulhas current of South Africa[J]. Natural Hazards, 1998, 17(2): 117-127.
[9]Masson D. A case study of wave-current interaction in a strong tidal current[J]. Journal of Physical Oceanography, 1996, 26(3): 359-372.
[10]Tolman H L. Effects of tides and storm surges on North Sea wind waves[J]. Journal of Physical Oceanography, 1991, 21(6): 766-781.
[11]Wang D W, Liu A K, Peng C Y, et al. Wave-current interaction near the Gulf Stream during the Surface Wave Dynamics Experiment[J]. Journal of Geophysical Research, 1994, 99(C3): 5065-5079.
[12]White B S, Fornberg B. On the chance of freak waves at the sea[J]. J Fluid Mech, 1998, 355: 113-138.
[13]Signell R P, Beardsley R C, Graber H C, et al. Effect of wave-current interaction on wind-driven circulation in narrow, shallow embayments[J]. Journal of Geophysical Research, 1990, 95(6): 9671-9678.
[14]Xie L, Liu H, Peng M. The effect of wave-current interactions on the storm surge and inundation in Charleston Harbor during Hurricane Hugo 1989[J]. Ocean Modelling, 2008, 20(3): 252-269.
[15]Xie L, Wu K, Pietrafesa L, et al. A numerical study of wave-current interaction through surface and bottom stresses: Wind-driven circulation in the South Atlantic Bight under uniform winds[J]. Journal of Geophysical Research, 2001, 106(C8): 16841-16855.
[16]贾岩, 尹宝树, 杨德周. 东中国海浪流相互作用对水位和波高影响的数值研究[J]. 海洋科学, 2009, 33(8): 82-86.
Jia Yan, Yin Baoshu, Yang Dezhou. A numerical study of the influence of wave-current interaction on water elevation and significant wave height in the East China Sea[J]. Marine Sciences, 2009, 33(8): 82-86.
[17]Guan C, Rey V, Forget P. Improvement of the WAM wave model and its application to the Rhne river mouth area [J]. Journal of Coastal Research, 1999, 15(4): 966-973.
[18]Haidvogel D B, Arango H, Budgell W P, et al. Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the Regional Ocean Modeling System[J]. Journal of Computational Physics, 2008, 227(7): 3595-3624.
[19]Shchepetkin A F, McWilliams J C. The regional ocean modeling system: A split-explicit, free-surface, topog-raphy-following coordinates ocean model[J]. Ocean Modelling, 2005, 9(4): 347-404.
[20]Ris R C, Booij N, Holthuijsen L H. A third-generation wave model for coastal regions, Part Ⅱ, Verification[J]. Journal of Geophysical Research, 1999, 104(C4): 7667-7681.
[21]Jacob R, Larson J, Ong E. M×N communication and parallel interpolation in CCSM using the model coupling toolkit[R]. Preprint ANL/MCSP1225-0205. Mathematics and Computer Science Division, Argonne National Laboratory, 2005:25.
[22]Larson J, Jacob R, Ong E. The model coupling toolkit: A new Fortran90 toolkit for building multiphysics parallel coupled models[R]. Preprint ANL/MCSP1208-1204. Mathematics and Computer Science Division, Argonne National Laboratory, 2004:25.
[23]孙一妹, 费建芳, 程小平, 等. WRF_ROMS-1.2中尺度海气耦合模式简介[J]. 海洋预报, 2010, 27(2): 82-88.
Sun Yimei, Fei Jianfang, Cheng Xiaoping, et al. Introduction of mesoscale air-ocean coupled model:WRF_ROMS-1.2[J]. Marine Forecasts, 2010, 27(2): 82-88.
[24]Flather R A. A tidal model of the north-west European continental shelf[J]. Memoires de la Societe Royale des Sciences de Liege, 1976, 10(6): 141-164.
[25]肖文军, 丁平兴, 胡克林. 潮汐和流影响下长江口波浪场数值计算[J]. 海洋工程, 2008, 26(4): 45-52.
Xiao Wenjun, Ding Pingxing, Hu Kelin. Numerical calculation of wave fields with tide and currents in Yangtze estuary[J]. The Ocean Engineering, 2008, 26(4): 45-52.
陈耀登,陈晓梦,闵锦忠,等. 各向异性背景场误差协方差构建及在“凡亚比”台风的应用[J]. 海洋学报, 2016, 38(9): 32-45, doi:10.3969/j.issn.0253-4193.2016.09.004
Chen Yaodeng, Chen Xiaomeng, Min Jinzhong, et al. Anisotropic background error covariance modelling and its application in Typhoon Fanapi[J]. Haiyang Xuebao, 2016, 38(9): 32-45, doi:10.3969/j.issn.0253-4193.2016.09.004
A study of the influence of wave-current interaction on significant wave height in the Northwestern Pacific
Liu Na1, Li Benxia1, Wang Hui1, Lv Honggang1
(1.KeyLaboratoryofResearchonMarineHazardsForecasting,NationalMarineEnvironmentalForecastingCenter,Beijing100081,China)
Strong ocean current in the Northwestern Pacific has significant impact on the characteristics and distribution of ocean wave, especially during typhoon. A coupled current-wave modeling system based on the ROMS model and SWAN model is applied to study the current-induced modulation of significant wave height by wave-current interaction during Typhoon Danas, Typhoon Nari and Typhoon Wipha through October 6-17, 2013. The results indicated that the ocean current had significant impact on the simulation of significant wave height in the coupled modeling system. The significant wave height is closer to buoy observation when wave and current are coupled. The maximum enhanced significant wave height due to current is up to 1 m. It’s indicated that the significant wave height always increases (decreases) when the wave direction is against (along) the background ocean current. And the effects of wave-current interactions are not only local but also spread a long distance with the propagation of wave. The wave-current coupled modeling system is important for wave forecasting in the Northwestern Pacific. The current induced in the coupled modeling system would contribute to high-precision ocean wave forecast.
wave-current interaction; significant wave height; typhoon; Northwestern Pacific
2015-07-15;
2015-11-04。
国家自然科学基金(41406013)。
刘娜(1982—),女,山东省青岛市人,副研究员,主要从事海洋环流动力学研究。E-mail:liuna@nmefc.gov.cn
P731.22
A
0253-4193(2016)09-0021-11
