表贴式永磁同步电机准稳态多参数在线辨识

刘金海　陈　为

(福州大学电气工程与自动化学院　福州　350116)



表贴式永磁同步电机准稳态多参数在线辨识

刘金海陈为

(福州大学电气工程与自动化学院福州350116)

针对永磁同步电机参数传统稳态辨识与动态辨识的不足，提出了准稳态辨识模型以及关于表贴式永磁同步电机的准稳态多参数在线辨识方法。该方法以遗忘因子递推最小二乘算法为基础，以误差分析为优化指导，辨识精度较高。该方法可同时辨识表贴式永磁同步电机3个电气参数，辨识速度快，计算量适中，适合工程应用。以DSP和智能功率模块为实验平台基础的实验研究验证了所提出方法的可行性与有效性。

永磁同步电机多参数准稳态在线辨识

0　引言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)具有高功率密度、高转矩电流比、高功率因数等特点，广泛应用于工业生产及人类日常生活中[1-4]。近些年来，新型电力电子功率器件、新型DSP器件、矢量控制及高频磁等技术的发展进一步强化了PMSM相关控制系统的应用广度与深度[5，6]。为保障PMSM较高的动静态性能，对其电流矢量合理控制很有必要，而这通常需要电机参数的支持。文献[7]将得到的电机参数用于控制器的PI值优化设计。文献[8，9]需要电机的定子电枢电阻及电感等参数支持PMSM无速度传感控制。不仅如此，考虑到系统安全问题，某些情况下需要通过监测电机参数以便间接获取电机温度信息或进行故障诊断。文献[10]提出了一种通过观测转子磁链间接观测转子温度的方法。文献[11]试图通过模型参考自适应法(Model Reference Adaptive System，MRAS)辨识定子电枢电阻间接获取定子温度信息。文献[12]通过扩展卡尔曼滤波法(Extended Kalman Filter，EKF)辨识定子电枢电阻，从而对电机进行开路故障诊断。运用现有一些方法可离线获取PMSM参数[13-15]，然而电机在线运行时，其参数一般随不同状态而变化。综上所述，对PMSM进行多参数在线辨识非常有必要。

依据电机工作的状态，PMSM参数辨识一般可分为动态辨识和稳态辨识两大类别。动态辨识一般基于PMSM动态电压方程，并借助相应辨识算法及“足够多有效数据”，从而辨识出相应的电机参数。数据“足够多”是指足够多有差异性的辨识数据，以便达成辨识数据集的满秩性，从而有利于辨识结果正确收敛。数据“有效”指：①干扰噪声足够小或无干扰噪声；②相位偏移足够小或无相位偏移。仿真很容易做到此处的数据“有效”，然而实际系统却很困难，原因是实际系统通常需要对传感器数据进行滤波处理，加之系统其他环节的传输延时，导致同拍辨识数据存在相位偏移，影响辨识结果。文献[16]研究了基于MRAS辨识法在线同时辨识PMSM三个参数，仿真结果显示参数辨识值具有较好的动态跟踪参数实际值的能力，但实际实验结果却显示定子电阻辨识值和永磁磁链辨识值无法正确收敛。有别于动态辨识，稳态辨识没有相位偏移的问题。原因是稳态辨识一般基于PMSM的稳态电压方程，方程不含微分项，方程中各状态量可视为直流量，则无所谓相位偏移。因此，稳态辨识成为PMSM参数辨识的研究趋势之一。

PMSM交直轴(d、q轴)稳态电压方程秩数为2，而方程含有定子电枢电阻、d轴和q轴电感、转子永磁磁链4个参数，即便是表贴式永磁同步电机(Surface Permanent Magnet Synchronous Motor，SPMSM)也有3个参数，因此方程是欠秩的。虽然递推最小二乘(Recursive Least-Square，RLS)、扩展卡尔曼滤波(EKF)、模型参考自适应(MRAS)、人工神经元(Artificial Neural Network，ANN)、演化(Evolutionary Algorithm，EA)等辨识算法已广泛应用于PMSM参数辨识领域，然而稳态电压方程欠秩，仅靠一种稳态输入输出数据无法确保辨识结果正确收敛[16]。针对该问题，现有主流的处理办法是注入d、q轴电流扰动信号来解决。注入q轴电流将引起输出转矩扰动，波及转速变化，则属动态辨识范畴，一般基于PMSM动态电压方程构造动态辨识模型，因此较难于避免由传感采样滤波等因素导致的同拍辨识数据不同步即相位偏移的问题，影响辨识精度。而注入d轴电流，对输出转矩影响可忽略，则属稳态辨识范畴，一般基于PMSM稳态电压方程构造稳态辨识模型，辨识效果较好，是当前主流研究方向。即便如此，在单步一次性辨识前提下，稳态注入d轴电流辨识法，一般也只辨识出1或2个电机参数；为了增加辨识参数的数量，通常要分多步辨识，而多步辨识较为繁锁，且需假定步与步过渡时相关参数的不变性。

结合PMSM动态辨识和稳态辨识各自优劣与特点，本文提出一种“准稳态”概念：d、q轴电流为稳态，转速可稳态也可动态，即将传统的稳态概念视为“准稳态”的子集。基于“准稳态”概念，提出一种关于表贴式永磁同步电机的准稳态多参数在线辨识方法(下文简称新方法)。新方法基于SPMSM的q轴电压方程构造“准稳态”辨识模型，结合遗忘因子递推最小二乘算法(Factor Recursive Least Squares，FRLS)，可同时辨识出SPMSM的定子电枢电阻、d轴和q轴电感和转子永磁磁链全部3个参数，且可有效规避动态辨识类法中同拍辨识数据相位偏移引起的辨识效果不佳的问题。新方法原理易理解，计算量适中，便于工程应用推广。实验研究验证了新方法的可行性和有效性。

1　准稳态辨识模型与误差分析

1.1准稳态辨识模型

为便于研究，PMSM一般可假定：忽略铁心磁饱和，电动势为正弦，忽略谐波因素，忽略涡流与磁滞引起的铁损，三相对称等。则在转子旋转坐标(d、q坐标)下，PMSM的动态电压方程为

(1)

磁链方程为

(2)

式中，ud、uq分别为d、q轴电压；id、iq分别为d、q轴电流；Ld、Lq分别为d、q轴电感；λd、λq分别为d、q轴磁链；p为微分算子；λr为转子永磁磁链；Rs为定子电枢电阻；ωe为电角速度。

式(2)代入式(1)整理得。

(3)

稳态条件下，电流微分为0，则有PMSM稳态电压方程

(4)

对于SPMSM而言，d、q轴电感相等，即Ld=Lq=L，那么其稳态电压方程为

(5)

由式(5)可知，SPMSM稳态d、q电压方程含有Rs、L、λr这3个完整的电机电气参数，且皆出现在q轴稳态电压方程中。那么，只要基于该q轴电压方程，合理构造辨识模型，利用相关辨识算法，即可完成对SPMSM完整3个参数的辨识。为便于分析,重写式(5)中的q轴电压方程为

uq=Rsiq+ωeLid+ωeλr

(6)

式(6)中要辨识的参数为3个，则应构造线性无关的至少3种稳态工作条件，进而构造稳态辨识模型，才能实现秩数为3的稳态满秩辨识，为辨识结果正确收敛提供理论保障。

式(6)中双稳态id可构造秩数为2的辨识模型，加之双稳态ωe可使辨识模型秩数达至3满秩，对应图1所示，取D1、D2及D3三种稳态时间段构造辨识模型进行参数辨识。然而就图1这种双转速阶跃解决方案而言，因空载或轻载D1、D2及D3稳态时间段下的q轴电流较小，加之Rs一般也很小，则电阻压降很小，由误差分析理论易知对Rs的辨识精度较低。为了提升辨识精度应设法提升q轴电流，在维持稳态的大前提条件下，只能通过提升负载转矩给定以达成条件，而这在实际工况下很可能是受限不允许的，且负载转矩给定装置将增加系统复杂性及成本，这也是当前业界的研究瓶颈之一。这主要是受传统电机学稳态概念的束缚，即稳态时相电流和相电压的幅值及频率应恒定，且电机转速恒定。

图1　双转速阶跃响应Fig.1　Two steps of speed response

深入比较式(3)与式(4)，发现二者的区别实际上不是稳态与否，而是方程中是否含有d、q轴电流的微分项，即式(4)中电角速度ωe可以是稳态不变，也可以是动态线性变化的；换言之，d、q轴电流为稳态，不管电机转速稳态与否，即上文提出的“准稳态”的概念。当电机转速稳态，“准稳态”即为稳态。当电机转速非稳态，“准稳态”为恒转矩加速或减速状态，此状态下d、q轴电流可近似恒定，由式(6)可知uq变化主要是由ωe引起，而相对电流环而言ωe是以机械时间常数为参照的大惯性变量，变化相对较慢，因此该状态下可忽略uq与ωe的相位偏移，则可入选辨识数据状态点。

图2为矢量控制下SPMSM空载单转速阶跃响应，取图中恒转矩加速状态某一状态点t1，对应式(6)实例化为

uq1=Rsiqm+ωe1λr

(7)

图2　单转速阶跃响应Fig.2　Single step of speed response

当SPMSM稳态空载转动时，分别令id>0及id=0，对应图2中的t2和t3两个时刻，则式(6)分别实例化为

uq2=Rsiq0+ωe2Lidm+ωe2λr

(8)

uq3=Rsiq0+ωe2λr

(9)

联立式(7)～式(9)解得

(10)

式(10)即为本文提出的准稳态辨识模型，基于该模型，可单步一次性辨识出SPMSM的3个参数，且含有可灵活调整的q轴饱和电流iqm，有利于提升Rs的辨识精度。

1.2误差分析

实际系统相关采样数据不可避免地存在误差，误差分析对辨识数据的选择及优化辨识精度具有重要的指导性意义。

依据准稳态辨识模型式(10)，对定子电枢电阻Rs误差分析，得其误差项为

ΔRs=

(11)

依据准稳态辨识模型式(10)，对定子d、q轴电感L误差分析，得其误差项为

(12)

由式(12)可见，增加d轴正注入电流idm可有效降低定子d、q轴电感L的误差量，进而提升辨识精度；反之减小idm，辨识精度将变差。

依据准稳态辨识模型式(10)，对转子永磁磁链λr进行误差分析，得其误差项为

(13)

式中

λr(iq0Δωe1+iqmΔωe2)

(14)

由式(14)可知，增加iqm和ωe2可有效降低转子永磁磁链误差，进而提升转子永磁磁链参数辨识精度；反之辨识精度变差。

2　准稳态多参数在线辨识方法

根据式(10)准稳态辨识模型及对应图2中的t1、t2、t3三个时刻的辨识数据可直接辨识出电机3个参数，然而这种点式的辨识结果，由于输入数据点太少，可靠性有限。多次辨识结果求平均值是一种解决方法，但数据累加存在溢出风险(特别是当用定点DSP实现时)，相比而言，更好的办法是借助于有效的迭代辨识算法。遗忘因子递推最小二乘法(FRLS)是一种高效易用的迭代辨识算法[25，26]，工程应用广泛，很适合SPMSM准稳态多参数在线辨识。

式(10)准稳态辨识模型是式(7)～式(9)三元一次方程组的解，而该方程组源自q轴电压方程式(6)及图2中t1、t2和t3三状态点的实例化，因此可以结合式(6)和FRLS构造迭代算法。FRLS的算法为[25]

θ(k)=θ(k-1)+K(k)[y(k)-φT(k)θ(k-1)]

(15)

式中，k为拍数；θ为参数辨识值(n维列向量)；φ为输入数据(n维列向量)；y为输出数据(标量)；K为中间量(n维列向量)；P为n维相关矩阵；λ为遗忘因子；I为n维单位矩阵。

具体结合式(6)，n=3，定义

y(k)=uq(k)

(16)

式(16)中输入数据φ和输出数据y的选择可参照式(10)及图2。为便于迭代，将图2中t1、t2和t3点式数据取值变为图3中D1、D2和D3数据带取值，以这3个数据带为式(16)的辨识数据，则可实现对电机3参数满秩辨识，数据带D1、D2和D3各含相同拍数的数据状态点，每拍数据状态点由各自的输入数据φ和输出数据y组成。

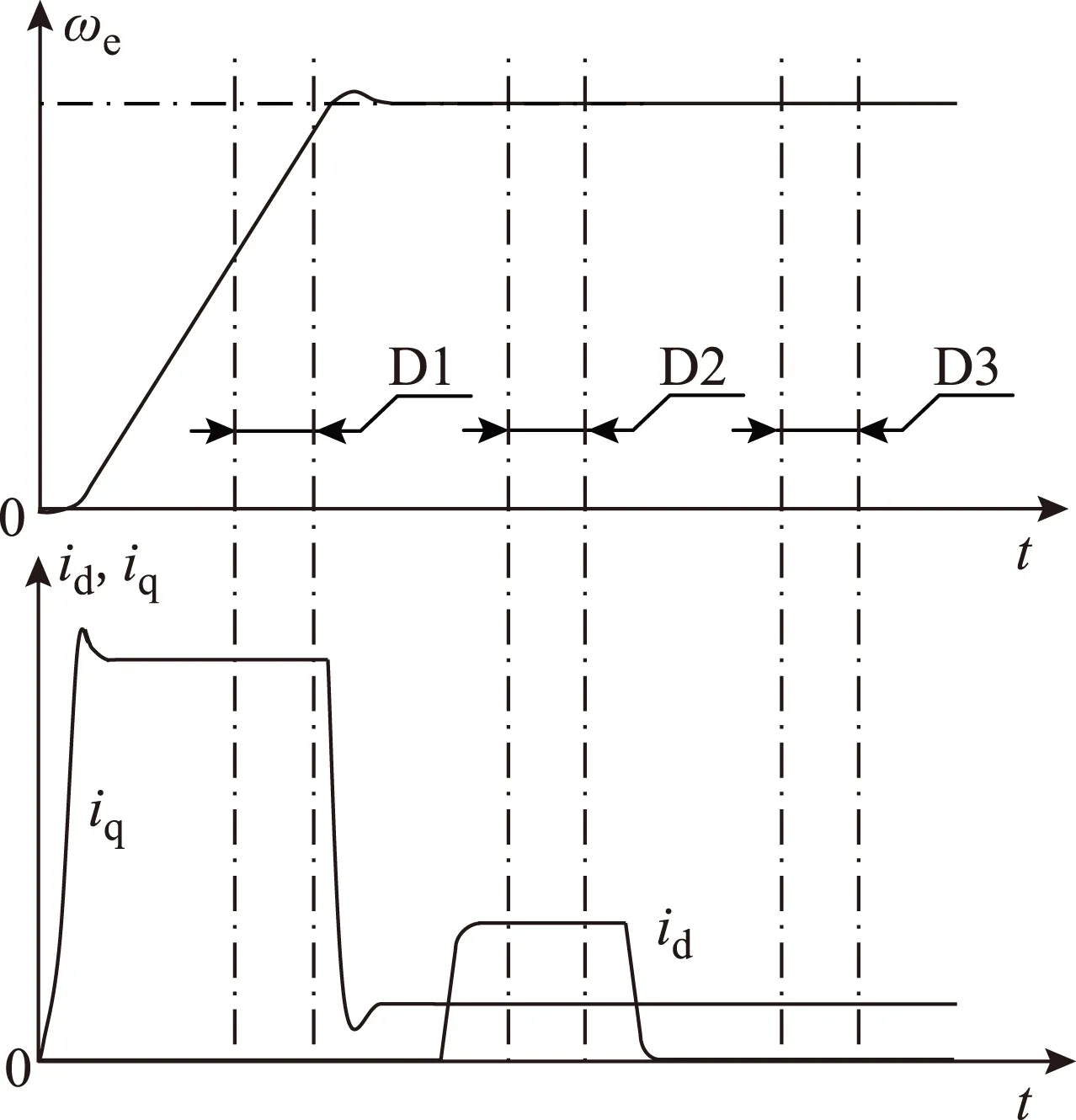
图3　单转速阶跃响应-数据带Fig.3　Single step of speed response-data segments

3　实验研究

为验证新方法的可行性与有效性，本文采用DSP控制器TMS320F2808和智能功率模块PS21867搭建硬件实验平台，实验电机参数：额定转速3 000 r/min，额定功率600 W，额定相电流幅值5.665 A，相电阻为1.12 Ω，交直轴电感L为2.91 mH，转子永磁磁链λr为0.075 Wb，极对数为4，转动惯量为0.425×10-3kg·m2，自带增量式光电编码器线数2 500 P/R。

本文提出的准稳态多参数在线辨识方法以磁场定向控制方式为基础，如图4所示，采用SVPWM调制方式。

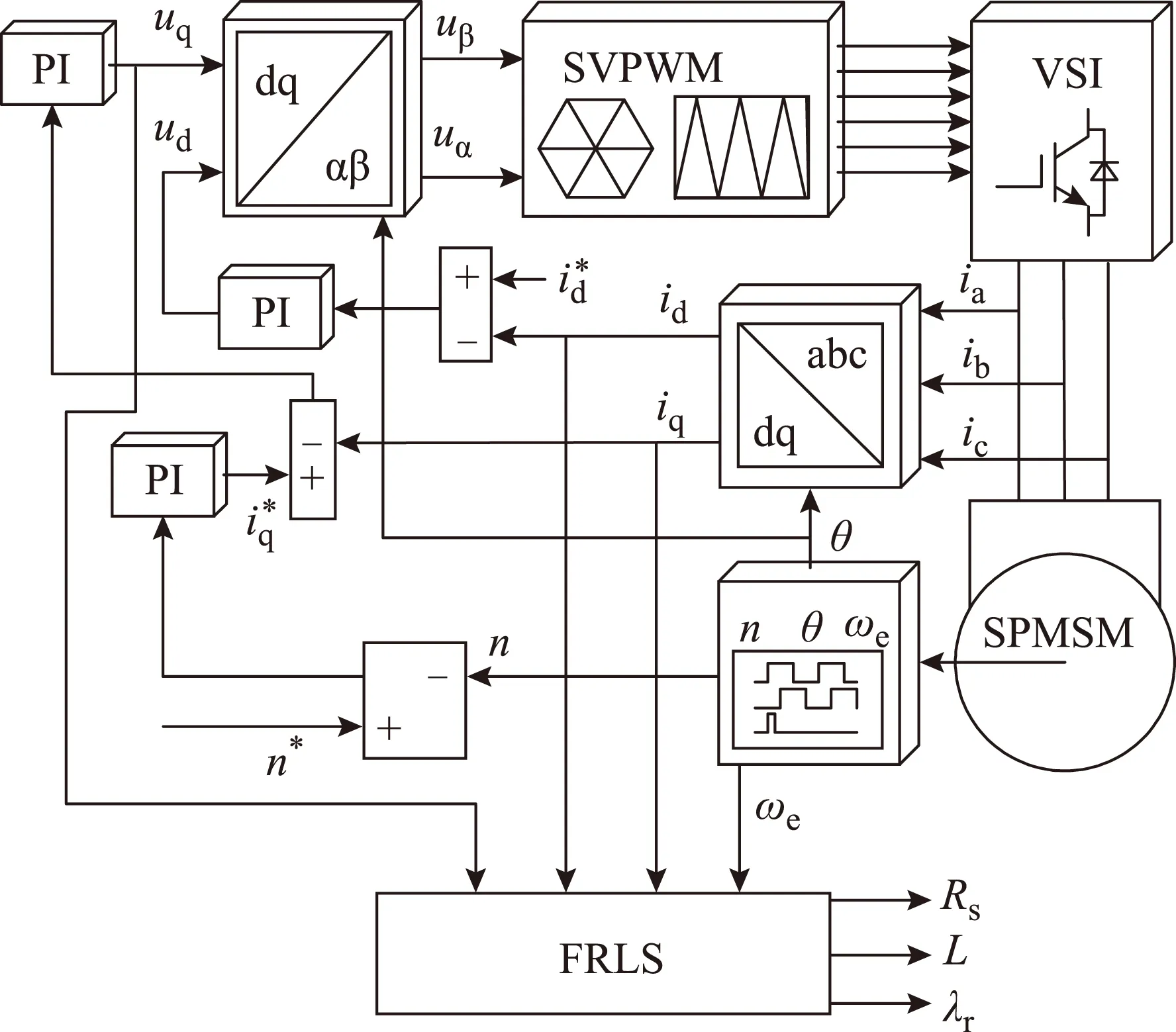
图4　系统控制框图Fig.4　Block diagram of system control

依据图3和图4及本文提出的准稳态辨识新方法，在硬件实验平台上进行在线参数辨识实验，取0～3 000 r/min转速阶跃、idm=6 A及iqm=5.81 A，参数辨识初始值均设置为0，辨识实验波形如图5～图7所示。

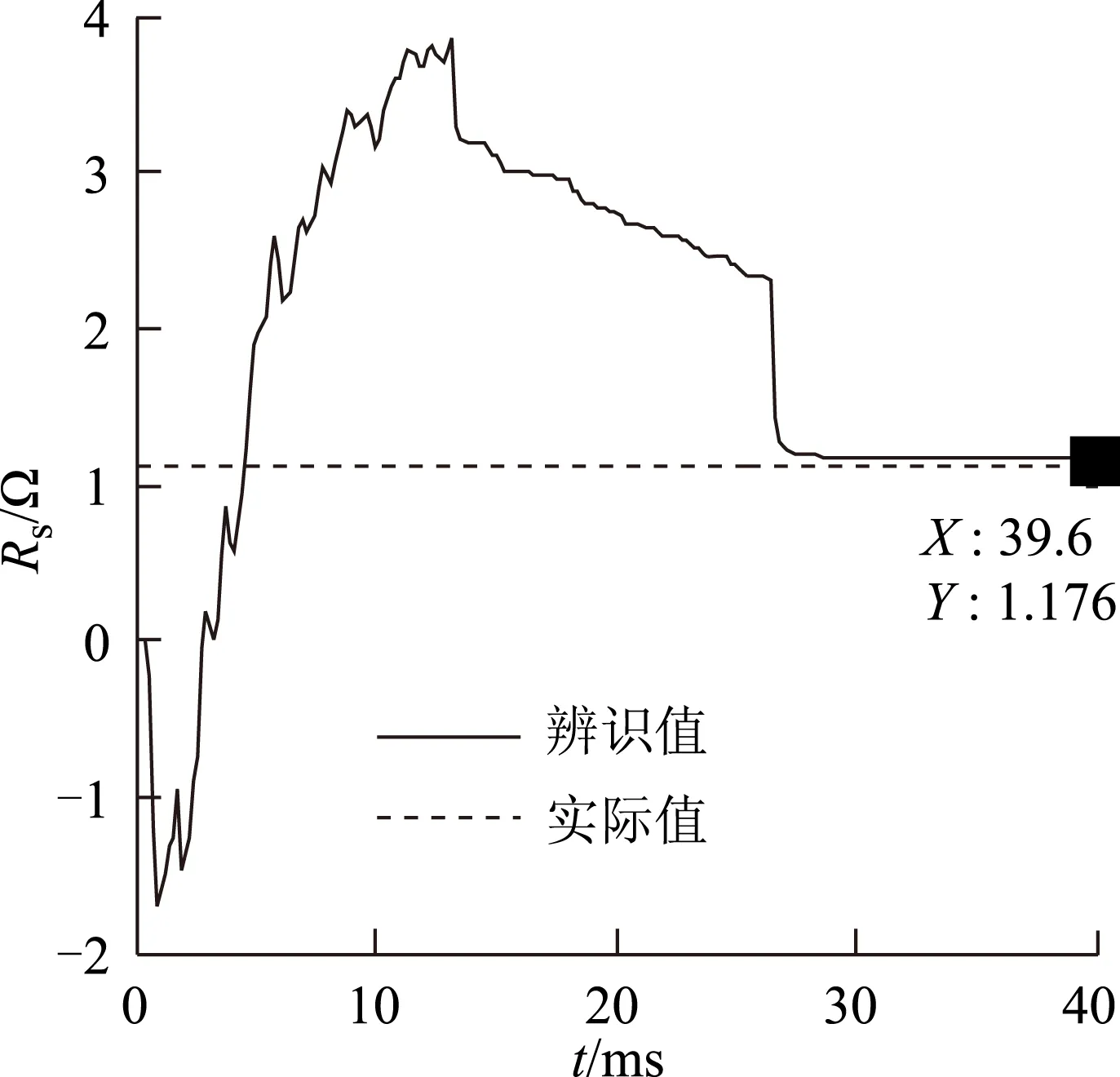
图5　Rs辨识实验波形Fig.5　The identification experiment wave of Rs

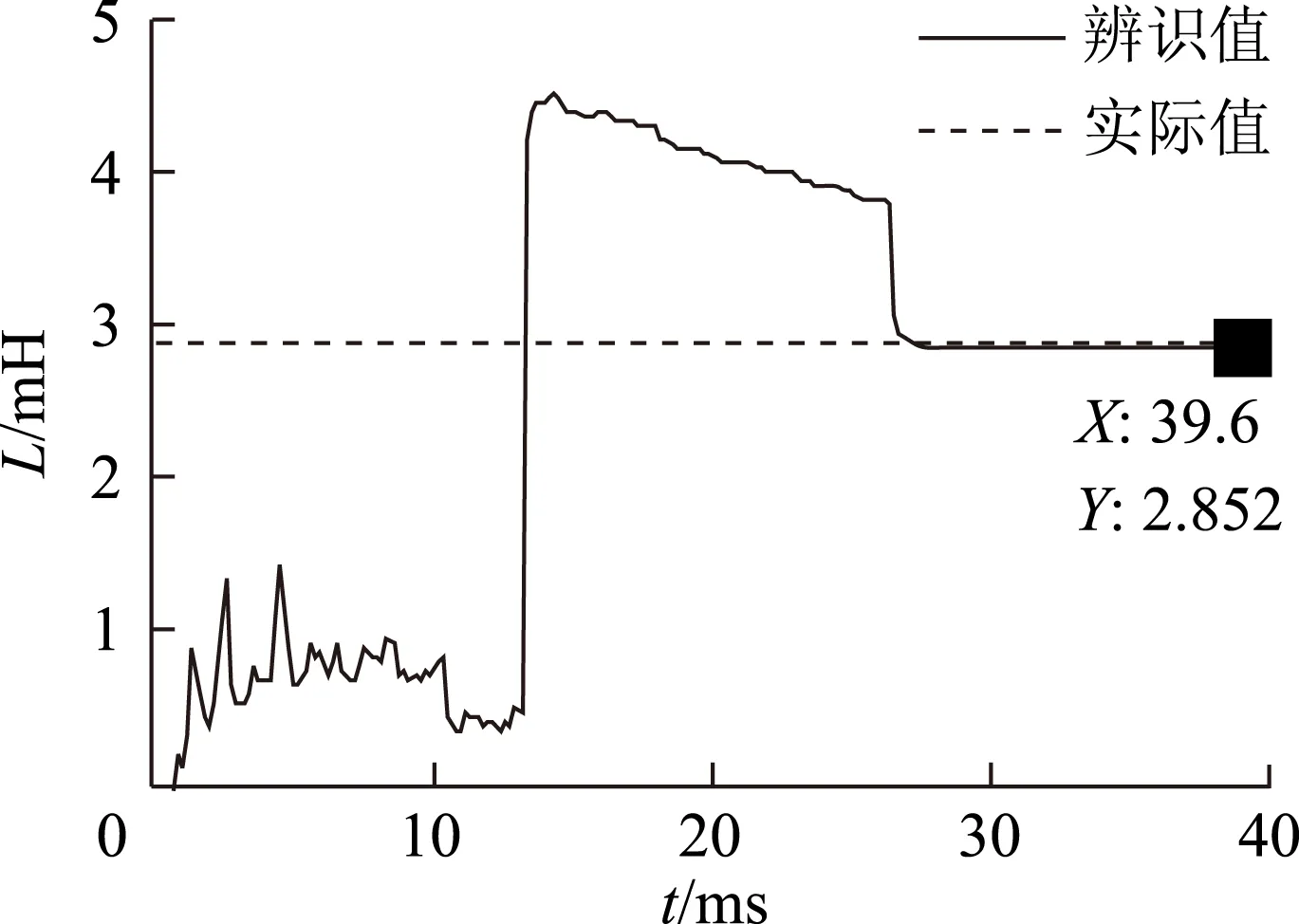
图6　L辨识实验波形Fig.6　The identification experiment wave of L

图7　λr辨识实验波形Fig.7　The identification experiment wave of λr

综合图5～图7实验结果可见辨识误差小，辨识效果好，三者有共同点：前2/3时间内辨识波形不收敛，后1/3时间辨识波形正确收敛。分析其原因：前2/3时间对应图3的D1和D2辨识数据区，是欠秩辨识，则无法正确收敛；后1/3时间对应图3的D3辨识数据区，然其之前已包含D1和D2辨识，则为满秩辨识，故波形正确收敛。

图8为不同idm和iqm组合下的Rs实验辨识结果。由图可见，中小电流iqm时Rs辨识误差较大，当采用大电流iqm时Rs辨识误差得到有效抑制，idm与Rs辨识误差无明显相关性。这与上文Rs的误差分析结论吻合。

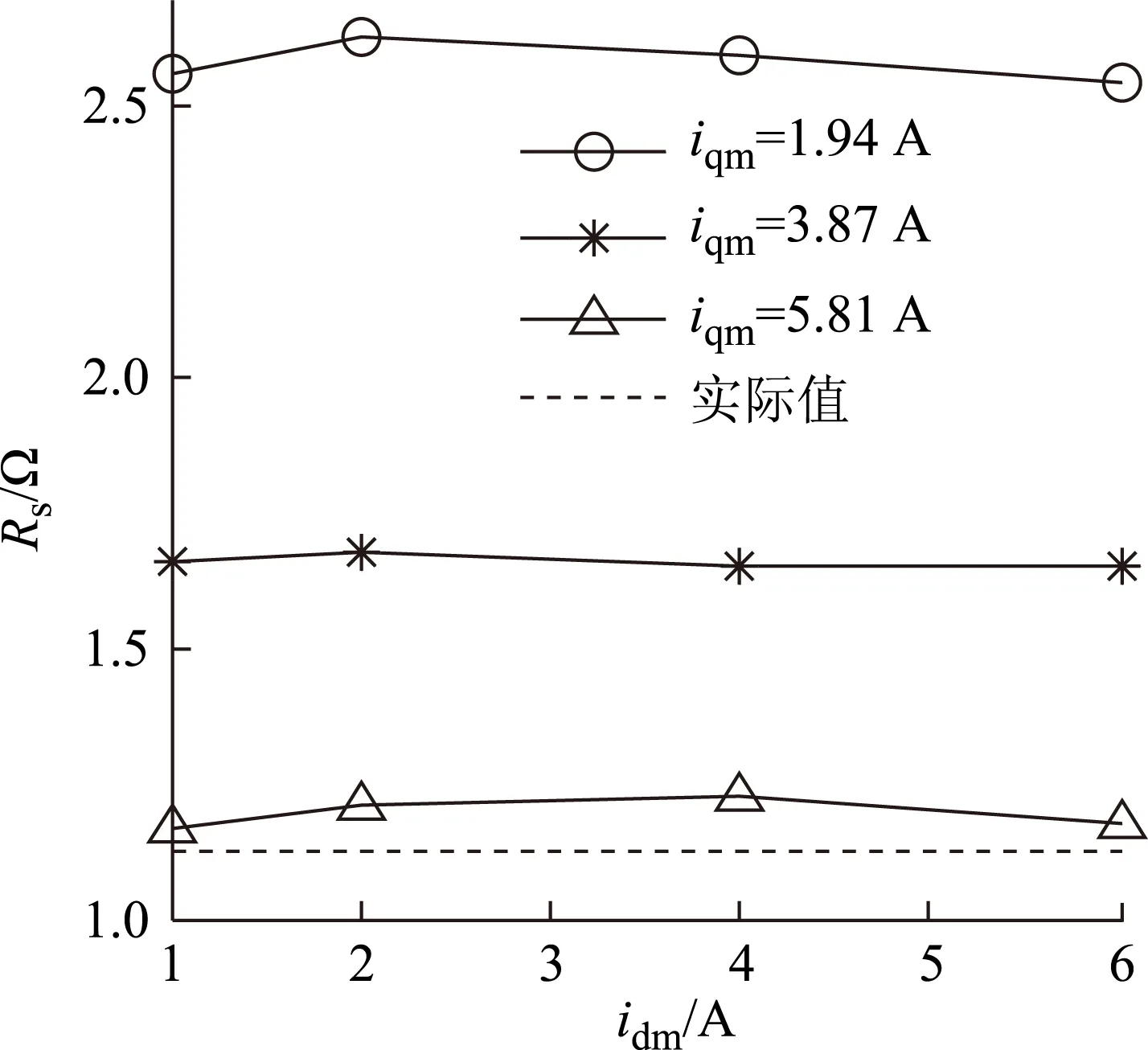
图8　Rs辨识实验结果(vs idm和iqm)Fig.8　The identification experiment results of Rs (vs idm & iqm)

图9为不同idm和iqm组合下的L辨识实验结果。由图可见，当小电流idm=1 A时L辨识误差相对较大，而当中等电流idm=2 A及4 A时L辨识误差相对较小，iqm与L辨识误差无明显相关性。这与上文L的误差分析结论基本吻合。而图9中idm=6 A对应图3中的D2状态，电机已轻度过载，实验结果显示L变小约2%，初步认为磁饱和可能是引起该变化的主要原因。关于磁饱和对本文方法L参数辨识的影响有待进一步研究。

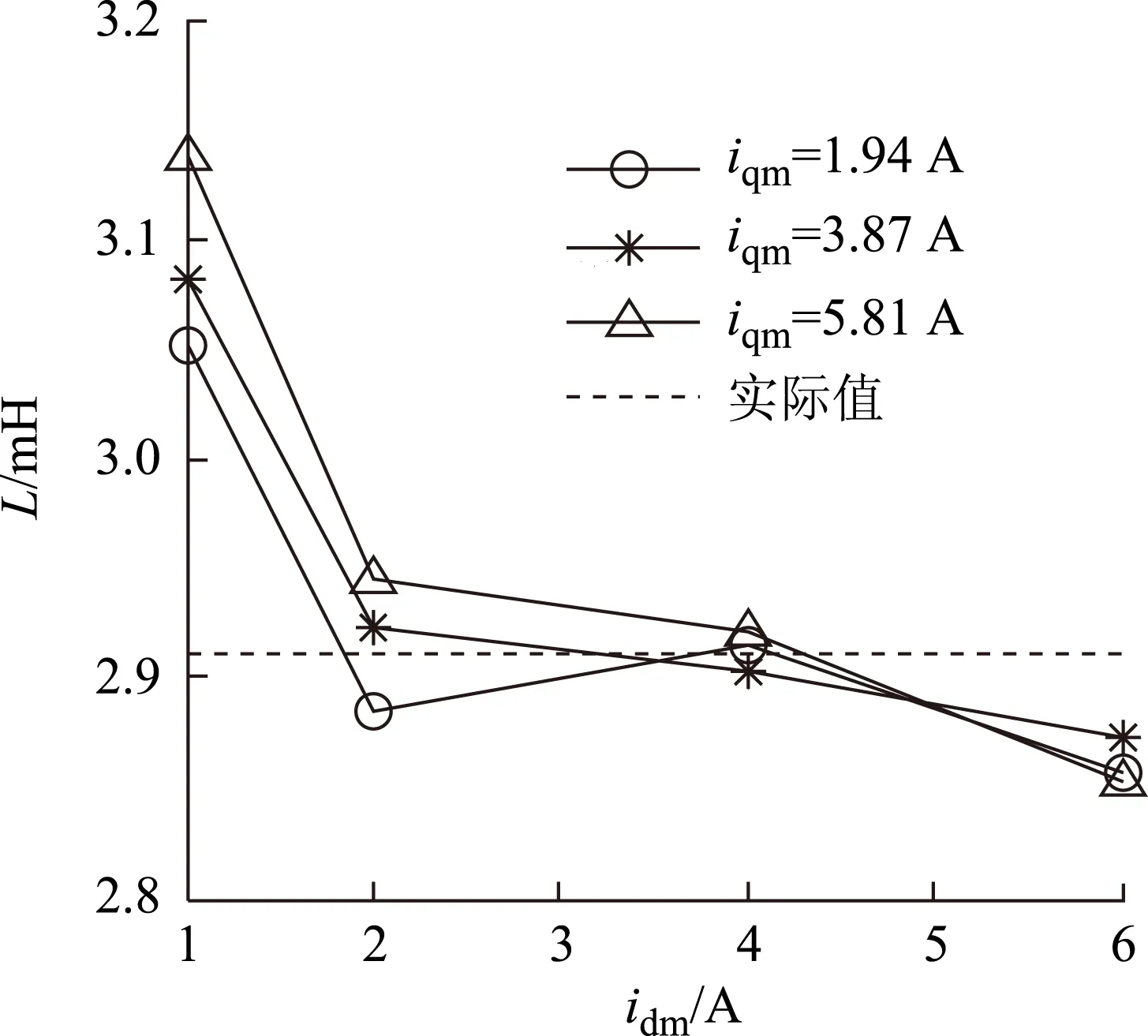
图9　L辨识实验结果(vs idm和iqm)Fig.9　The identification experiment results of L (vs idm & iqm)

图10为不同idm和iqm组合下的λr实验辨识结果。由图可见，电流iqm变大时λr辨识误差变小，idm与λr辨识误差无明显相关性。这与上文λr的误差分析结论基本吻合。此外总体上不同idm和λqm组合的λr辨识误差较小，最大误差也不足3%，有较高的辨识精度，其原因是中高速条件下λr引起的压降是式(6)中uq的主要组成成份。

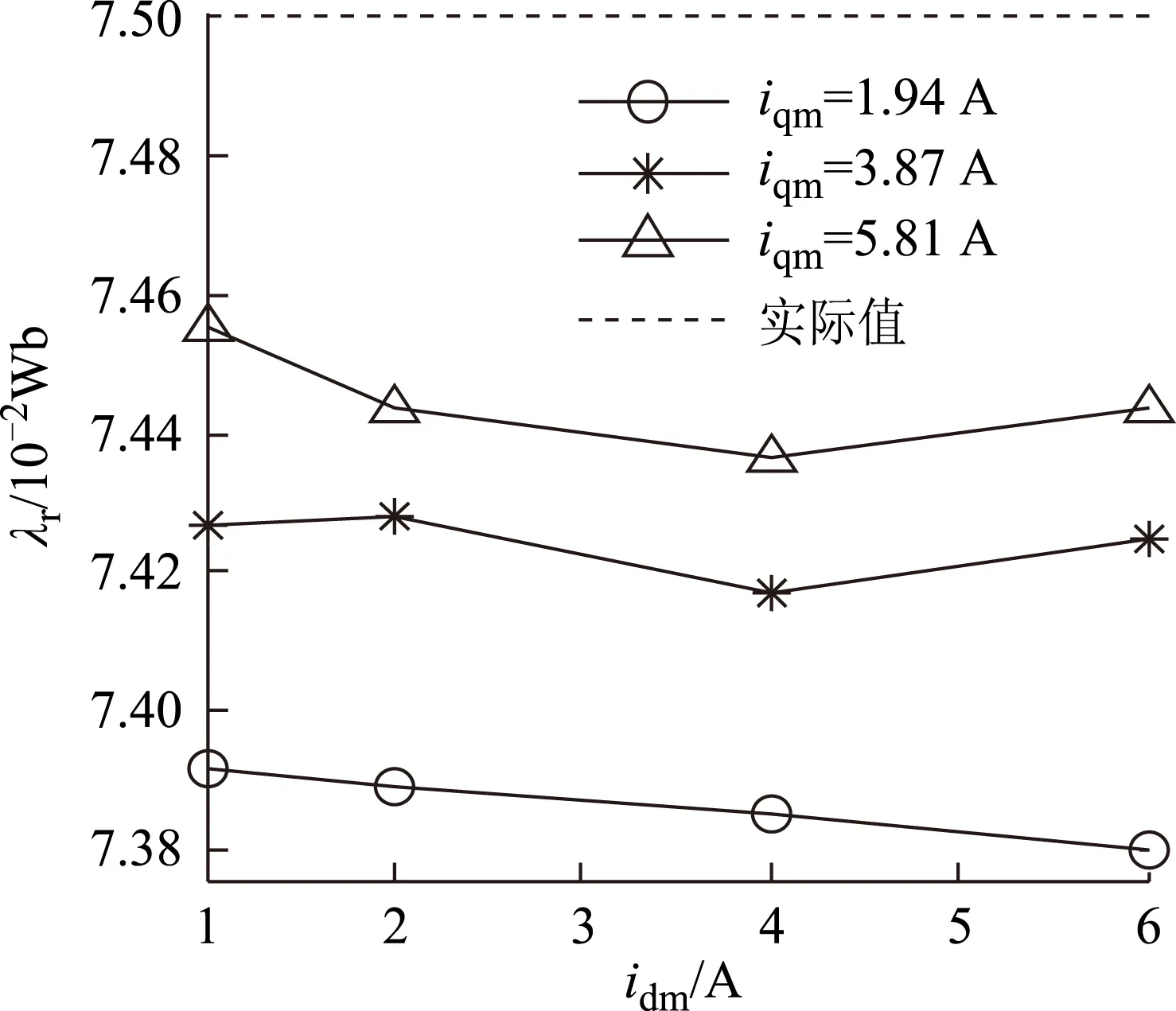
图10　λr辨识实验结果(vs idm和iqm)Fig.10　The identification experiment results of λr (vs idm & iqm)

4　结论

本文针对永磁同步电机参数传统稳态辨识与动态辨识的不足，提出了准稳态辨识模型概念，进而提出了关于表贴式永磁同步电机的准稳态多参数在线辨识新方法，可一次性辨识出电机的3个电气参数。新方法中的误差分析对提升辨识精度具有重要指导意义。新方法以遗忘因子递推最小二乘法为基础，有较高辨识精度，收敛速度快，计算量适中，适合工程应用。实验研究进一步验证了新方法的可行性和有效性。

[1]Jahns T M，Kliman G B，Neumann T W.Interior permanent-magnet synchronous motors for adjustable-speed drives[J].IEEE Transactions on Industry Applications，1986，IA-22(4)：738-747.

[2]Pillay P，Krishnan R.Modeling，simulation，and analysis of permanent-magnet motor drives，part Ⅰ：the permanent-magnet synchronous motor drive[J].IEEE Transactions on Industry Applications，1989，25(2)：265-273.

[3]Uddin M N，Abido M A，Rahman M A.Development and implementation of a hybrid intelligent controller for interior permanent-magnet synchronous motor drives[J].IEEE Transactions on Industry Applications，2004，40(1)：68-76.

[4]王宏，于泳，徐殿国．永磁同步电机位置伺服系统[J].中国电机工程学报，2004，24(7)：151-155.

Wang Hong，Yu Yong，Xu Dianguo.The position servo system of PMSM[J].Proceedings of the CSEE，2004，24(7)：151-155.

[5]Blaschke F.The principle of field orientation as applied to the new transvektor closed-loop control system for rotating-field machines[J].Siemens Review，1972，34(5)：217-220.

[6]陈为，何建农.电力电子高频磁技术及其发展趋势[J].电工电能新技术，2000，19(2)：30-34.

Chen Wei，He Jiannong.Power electronics high- frequency magnetics technology and their development[J].Advanced Technology of Electrical Engineering and Energy，2000，19(2)：30-34.

[7]Senjyu T，Urasaki N，Uezato K.Parameter measurement for PMSM using adaptive identification[C]//Proceedings of the IEEE International Symposium on Industrial Electronics，L’Aquila,2002，3：711-716.

[8]Bolognani S，Oboe R，Zigliotto M.Sensorless full-digital PMSM drive with EKF estimation of speed and rotor position[J].IEEE Transactions on Industrial Electronics，1999，46(1)：184-191.

[9]Nguyen K Q，Nguyen T H，Ha Q P.FPGa-based sensorless PMSM speed control using reduced-order extended kalman filters[J].IEEE Transactions on Industrial Electronics，2014，61(12)：6574-6582.

[10]Specht A，Bocker J.Observer for the rotor temperature of IPMSM[C]//14th International IEEE International Power Electronics and Motion Control Conference，Ohrid，2010：T4-12-T4-15.

[11]Wang Z F，Teng Q Z，Zhang C N，et al.Real-time PMSM temperature rising in electric vehicles with MRAS[C]//WRI Global Congress on the Intelligent Systems，Xiamen，2009：66-70.

[12]Ahn S G，Park B G，Kim R Y，et al.Fault diagnosis for open-phase faults of permanent magnet synchronous motor drives using extended kalman filter[C]//36th Annual Conference on IEEE Industrial Electronics Society，Glendale，AZ，2010：835-840.

[13]刘金海，陈为，胡金高.永磁同步电机dq电感参数新实验获取法[J].电工技术学报，2014，29(7)：97-103.

Liu Jinhai，Chen Wei，Hu Jingao.Novel experimental methods of acquiring dq Inductances of a permanent magnet synchronous motor[J].Transactions of China Electrotechnical Society，2014，29(7)：97-103.

[14]陈振锋，钟彦儒，李洁.嵌入式永磁同步电机离线参数辨识技术[J].电力电子技术，2009，43(11)：43-44.

Chen Zhenfeng，Zhong Yanru，Li Jie.An off-line parameter estimation technique for permanent magnet synchronous motor[J].Power Electronics，2009，43(11)：43-44.

[15]唐斌，游林儒，黄招彬.一种改进的静止型永磁同步电机离线参数辨识方法[J].微电机，2014，47(4)：49-54.

Tang Bin，You Linru，Huang Zhaobin.An improved offline parameter identification strategy at standstill for PMSM[J].Micromotors，2014，47(4)：49-54.

[16]刘侃.永磁同步电机多参数在线辨识研究[D].长沙：湖南大学，2011.

[17]Hag-Wone K，Myung-Joong Y，Kwan-Yuhl C，et al.Nonlinearity estimation and compensation of PWM VSI for PMSM under resistance and flux linkage uncertainty[J].IEEE Transactions on Control Systems Technology，2006，14(4)：589-601.

[18]Kim H S，Kim K H，Youn M J.On-line dead-time compensation method based on time delay control[J].IEEE Transactions on Control Systems Technology，2003，11(2)：279-285.

[19]倪超，陈斌.一种逆变器死区效应补偿方法[J].电力电子技术，2010，44(11)：75-77.

Ni Chao，Chen Bin.A kind of inverter dead time effect compensation[J].Power Electronics，2010，44(11)：75-77.

[20]乔鸣忠，夏益辉，朱鹏，等.基于电流闭环和死区补偿的变频驱动调速系统低频振荡抑制[J].电工技术学报，2014，29(11)：126-133.

Qiao Mingzhong，Xia Yihui，Zhu Peng，et al.Low-frequency oscillation restrain method of induction motor fed by inverter based on current close-loop and dead-time compensation[J].Transactions of China Electrotechnical Society，2014，29(11)：126-133.

[21]陈斌，王婷，吕征宇，等.电压型逆变器非线性的分析及补偿[J].电工技术学报，2014，29(6)：24-30.

Chen Bin，Wang Ting，Lü Zhengyu，et al.The analysis and compensation of voltage source inverter nonlinearity[J].Transactions of China Electrotechnical Society，2014，29(6)：24-30.

[22]袁佳歆，薛钢，赵震，等.三相逆变器无死区最优矢量控制研究[J].电力系统保护与控制，2014，42(24)：18-24.

Yuan Jiaxin，Xue Gang，Zhao Zhen，et al.New optimal dead-time elimination for three-phase voltage source inverters[J].Power System Protection and Control，2014，42(24)：18-24.

[23]张健康，粟小华，胡勇，等.智能变电站保护用电流互感器配置问题及解决措施[J].电力系统保护与控制，2014，42(7)：140-145.Zhang Jiankang，Su Xiaohua，Hu Yong，et al.Problems and solutions of configuration scheme of current transformer used by protection in smart substation[J].Power System Protection and Control，2014，42(7)：140-145.

[24]张宇辉，李哲，李天云，等.次同步谐振的变尺度全方位扫描Duffing振子检测方法[J].电力系统保护与控制，2014，42(14)：122-127.Zhang Yuhui，Li Zhe，Li Tianyun，et al.Subsynchronous resonance variable scale and comprehensive scanning Duffing oscillator detection method[J].Power System Protection and Control，2014，42(14)：122-127.

[25]庞中红，崔红.系统辨识与自适应控制MATLAB仿真[M].北京：北京航空航天大学出版社，2013.

[26]刘金琨，沈晓蓉，赵龙.系统辨识理论及Matlab仿真[M].北京：电子工业出版社，2013.

Online Multi-Parameter Identification for Surface-Mounted Permanent Magnet Synchronous Motors Under Quasi-Steady-State

Liu JinhaiChen Wei

(Colloge of Electrical Engineering and AutomationFuzhou UniversityFuzhou350116China)

The quasi-steady-state model for identification and the new method of online multi-parameter identification for surface-mounted permanent magnet synchronous motors under quasi-steady-state are presented in order to overcome the deficiency of the traditional parameter identification for permanent magnet synchronous motors under steady and dynamic states.The new method is based on the forgetting factor recursive least squares (FRLS) algorithm and has enough precision of identification with the guide of error analysis for optimization.The complete three electrical parameters of surface-mounted permanent magnet synchronous motors can be quickly and simultaneously identified with the new method，which has acceptable computational complexity and is suitable for the engineering applications.The experiment study verifies the feasibility and validity of the method，which was implemented on the experiment platform based on DSP and intelligent power module.

Permanent magnet synchronous motor，multi-parameter，quasi-steady-state，online identification

2015-05-13改稿日期2015-08-29

TM351

刘金海男，1982年生，博士研究生，讲师，研究方向为电气传动、电力电子技术。

E-mail：akljh007@163.com(通信作者)

陈为男，1958年生，教授，博士生导师，研究方向电力电子功率变换、高频磁技术、电磁兼容诊断与滤波器、电磁场分析与应用和电磁检测及其控制。

E-mail：chw@fzu.edu.cn

国家自然科学基金(51277032)和福建省中青年教师教育科研项目基金(JA15299)资助项目。