不平衡电网电压下基于滑模变结构控制的双馈风电系统转子侧变流器控制策略

张　迪　魏艳君　杨宗丰　丁　浩　漆汉宏

(燕山大学电气工程学院　秦皇岛　066004)



不平衡电网电压下基于滑模变结构控制的双馈风电系统转子侧变流器控制策略

张迪魏艳君杨宗丰丁浩漆汉宏

(燕山大学电气工程学院秦皇岛066004)

在两相静止坐标系下，建立了基于功率控制的双馈电机统一的数学模型，该模型在平衡和不平衡电网电压条件下均适用。采用基于滑模变结构的直接功率控制方法实现了对双馈风电系统转子侧变流器的控制，该方法控制结构简单，动态响应快，鲁棒性强。在不平衡电网电压条件下，提出了一种新型的功率优化补偿控制策略。该控制策略可直接对转子侧变换器的功率给定进行补偿，无需对定、转子电流进行正、负序分解，简化了系统控制结构；更重要的是其能有效降低定子电流扰动对功率补偿量的影响，系统鲁棒性得到明显提高。仿真和实验结果均证明了该控制策略的正确性和有效性。

双馈电机转子侧变换器滑模变结构控制直接功率控制不平衡电网电压

0　引言

近年来，随着新能源技术的快速发展，风力发电技术取得了长足的进步。双馈风电系统因具有变流器容量低、调速范围宽等优点，在许多场合尤其是大功率领域得到广泛应用[1]。

双馈风电系统的变流器多由两个三相两电平电压型PWM变换器组成，它们通过直流母线以背靠背的方式进行连接，按照其位置分别称为网侧变换器(Grid-side Converter，GSC)和转子侧变换器(Rotor-side Converter，RSC)，如图1所示。这种结构具有电流谐波含量低、功率可双向流动、功率因数可调等优点。同时，两个变换器通过直流母线电容实现解耦，可以分开独立控制而不受干扰[2]。

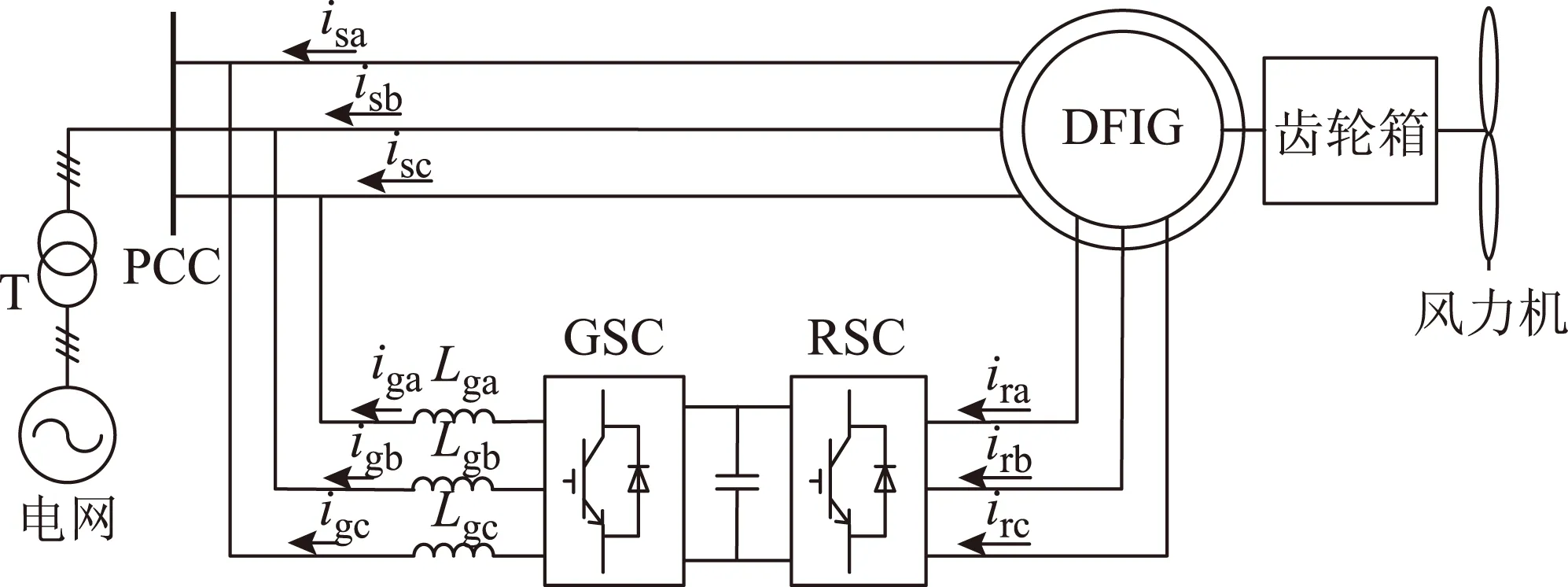
图1　双馈风电系统拓扑结构Fig.1　Structure of a DFIG-based wind-power generation system

转子侧变换器的一端与直流母线相连，另一端接入双馈电机转子绕组，其主要作用是控制双馈电机输出的有功功率和无功功率，以实现系统的最大风能追踪，保证并网系统运行的稳定性。

目前，转子侧变换器主要采用的是基于定子电压定向或定子磁链定向的矢量控制技术。这类方法可以实现系统有功功率和无功功率的独立控制，且稳态性能良好。然而，随着近年来我国经济的快速发展，大量非线性、冲击性和不对称性负荷不断地接入电网，电能质量状况日趋恶化；再伴随着各种电力系统故障的发生，谐波、电压跌落、电压不平衡等电能质量问题尤为严重[3]。在电网电压不平衡条件下，传统的矢量控制技术已无法满足系统的控制要求。基于矢量控制的改进的转子侧变换器控制策略的相关研究已相当成熟[4，5]，但由于其控制多在两相旋转坐标系下进行，需要获取电网电压相位信息并进行旋转坐标变换，同时还要考虑电压和电流的正、负序分量，控制系统结构往往比较复杂。而直接功率控制技术(Direct Power Control，DPC)因具有控制结构简单、动态响应快、鲁棒性好等优点，近年来得到了广泛关注[6-8]。文献[9]提出了一种能够在不平衡电网电压条件下消除电磁转矩振荡，同时保证并网电流正弦的直接功率控制策略。但该策略采用的是基于查表法的直接功率控制(LUT-DPC)，通过滞环实现，存在开关频率不恒定的缺点，给滤波器的设计带来一些困难。文献[10]提出了一种基于滑模变结构控制(Sliding-Mode Control，SMC)的双馈电机直接功率控制策略，采用基于SVPWM的定频调制方案实现，便于进行功率变换器和滤波器设计。另外该控制方法无需同步坐标变换，同时不存在电流环，大大简化了控制结构，提高了系统动态性能。但该控制方案是在理想电网条件下提出的。文献[11]在不平衡电网条件下，采用比例积分控制器与谐振调节器相结合的直接功率控制方案，实现了对电网故障下基频与二倍频功率振荡量的有效调节。文献[12，13]在非理想电网条件下，采用基于滑模变结构直接转矩控制策略来消除双馈电机的电磁转矩波动，并通过网侧变换器补偿定子电流谐波以确保系统输出的总电流保持正弦。文献[14]分析了传统的理想电网条件下基于滑模变结构的直接功率控制策略在电网电压不平衡情况下的状态特性，提出了一种适用于不平衡电网电压的基于滑模变结构的直接功率控制方案。该方案在两相静止坐标系下实现，无需进行坐标变换和电网的锁相。但该方法需对磁链进行估算，同时还需对定子电压和电流同时进行正、负序分解，系统结构略显复杂，在控制器控制效果不理想的情况下，功率补偿准确度还易受到定子电流扰动的影响。

本文在两相静止坐标系下建立了基于功率控制的双馈电机统一数学模型，设计了基于滑模变结构的直接功率控制方法；通过对不平衡电网电压下双馈电机输出功率进行分析，提出了一种新型的功率优化补偿控制策略，该补偿控制策略可直接对转子变换器的功率给定进行补偿，更重要的是其无需对定、转子电流进行正、负序分解，消除了定子电流扰动对功率补偿准确度的影响，同时系统控制结构也得到简化，可以满足双馈风电系统在各类运行工况下的并网要求。

1　不平衡电网电压下双馈电机数学模型

两相静止坐标系下双馈电机的数学模型为

(1)

式中，esα、esβ分别为定子电压的α、β轴分量，V；urα、urβ分别为转子电压的α、β轴分量，V；isα、isβ分别为定子电流的α、β轴分量，A；irα、irβ分别为转子电流的α、β轴分量，A；Rs、Rr分别为定、转子绕组电阻，Ω；Ls、Lr分别为两相静止坐标系中定、转子等效两相绕组自感，H；Lm为两相静止坐标系中定、转子同轴等效绕组间的互感，H；ωr为双馈电机转子旋转角速度，rad/s。

式(1)推导过程中未对运行条件做任何假设，可适用于电网电压波动、不平衡和谐波畸变等各种情况。将式(1)改写为定子电流状态方程的形式，可得

(2)

式中

双馈电机定子输出的瞬时有功和无功功率分别为

(3)

对式(3)求导，可得

(4)

在不平衡电网电压条件下，电网电压含有正序、负序与零序电压分量。由于本文所研究的双馈风电系统多为三相三线制结构，因此不含零序分量，在不平衡电网电压下对双馈电机的数学模型进行分析时只需考虑正序和负序分量。根据叠加原理，双馈电机两相静止坐标系下等效电路可分解为正序与负序部分，如图2所示。

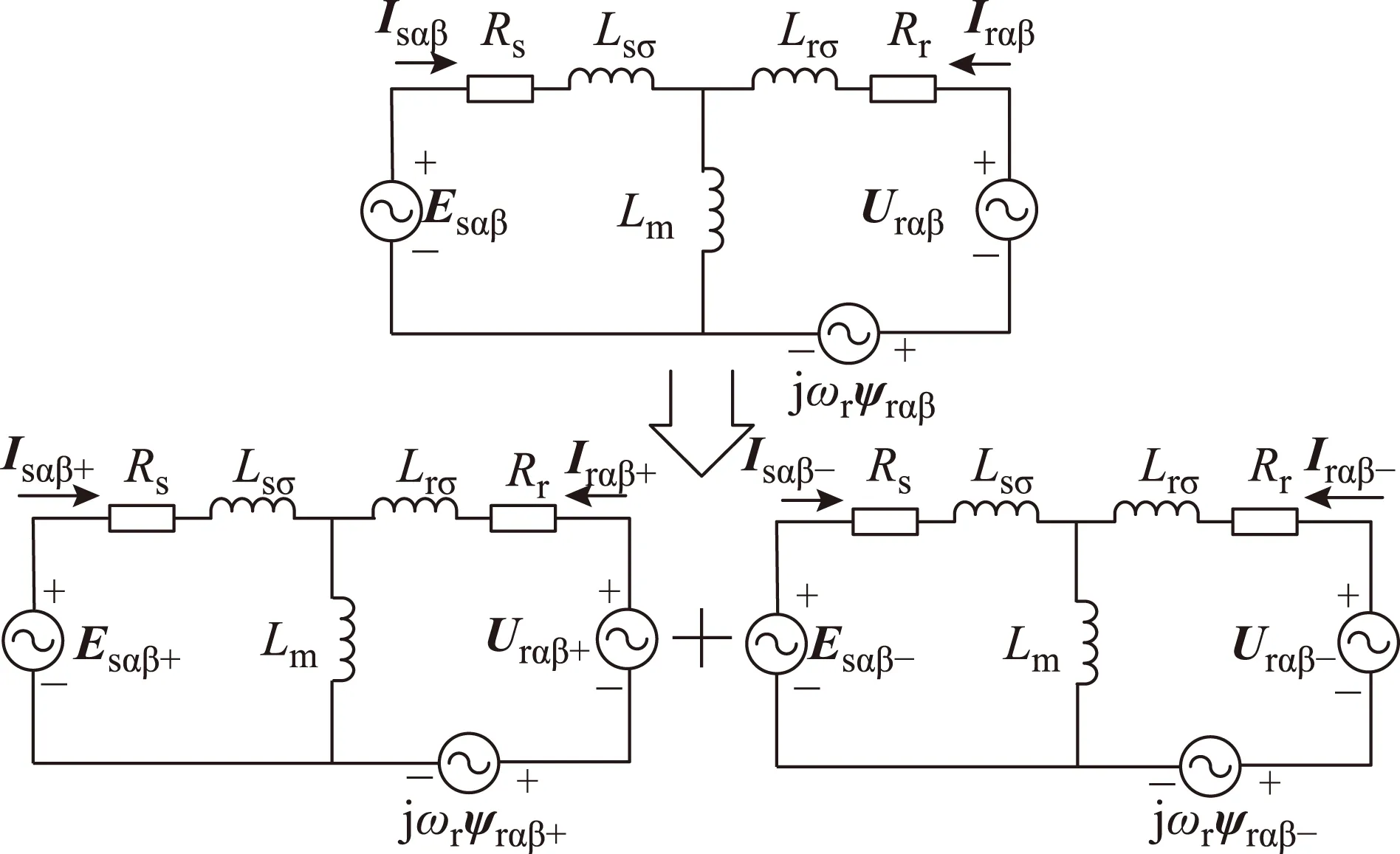
图2　不平衡电网电压条件下双馈电机等效电路Fig.2　The equivalent circuit of DFIG under unbalanced grid voltage conditions

由图2可知，不平衡电网电压条件下，电网电压可分解为正序、负序之和

Esαβ=Esαβ++Esαβ-=esα+jesβ

=(esα++esα-)+j(esβ++esβ-)

(5)

式中，Esαβ+、Esαβ-分别为电网电压正、负序矢量。

在电网电压不平衡条件下，电网电压的正、负序分量可分别描述为

(6)

由式(6)可得到电网电压α和β轴正、负序分量的变化率的表达式为

(7)

进而可得到

(8)

将式(2)与式(8)代入到式(4)中，即可得到在不平衡电网电压下，基于功率控制的双馈电机数学模型的状态空间表达式为

(9)

式中，ωslip为转差角频率，rad/s。

从式(9)中可知，式中的最后一个附加项是与电网电压负序分量有关的量，若电网电压负序分量为零，该附加项也变为零，此时的数学模型表达式即为理想电网电压条件下双馈电机的数学模型。因此，式(9)可作为双馈电机基于功率控制的统一的数学模型，该模型在平衡和不平衡电网电压条件下均适用。

2　不平衡电网电压下基于滑模变结构直接功率控制的转子侧变换器控制策略

2.1基于滑模变结构的转子侧变换器控制策略

滑模控制具有良好的鲁棒性，直接功率控制具有结构简单、响应速度快等优点。本文将滑模控制与直接功率控制结合(SMC-DPC)，这种控制策略集合了两种控制方法的优点，兼顾了系统的动态和稳态性能。

在系统运行过程中，滑模变结构控制系统运行包含到达过程与滑动过程两个阶段。系统的初始状态通常远离滑模面，系统由启动到系统状态变量运动至滑模面的过程称为到达过程。系统状态在滑模面上运动，滑动至平衡点的过程为滑动过程。到达过程与滑动过程共同决定系统的响应速度[15]。

滑模变结构控制系统中首先需要定义滑模面函数，通过对滑模面函数正负的判断，不断调整控制量以改变系统状态变量，使系统状态变量运行到滑模面，并沿滑模面滑动至平衡点。

结合直接功率控制的要求，定义滑模面函数为

(10)

式中，S1、S2分别为有功和无功功率的滑模面；Ps_ref、Ps分别为有功功率参考量与反馈量，W；Qs_ref、Qs分别为无功功率参考量与反馈量，var。

当系统有功功率、无功功率精准跟踪功率给定时，其变化率为零，有

(11)

将式(11)代入到式(9)中，经过变换可得

(12)

式中

R2=LmRr(esβirα-esαirβ)+LmLrωr(esαirα+esβirβ)

式(12)即为采用SMC-DPC进行控制的控制方程；此方程实现了有功和无功功率的解耦控制，通过合理设计滑模控制器，即可通过转子侧变流器控制双馈电机运行。

采用指数趋近律设计滑模控制器，可得

(13)

式中，K11、K12、K21和K22为正的控制参数；sgn(S1)和sgn(S2)为符号参数。

为了减小系统在滑模面切换过程可能出现的高频抖动，采用饱和函数代替式(13)中滑模控制器的符号函数，式(13)改写为

(14)

式中，sat(S1)和sat(S2)为饱和函数。

(15)

式中，λi为误差带，i=1，2。

根据式(13)～式(15)，重写SMC-DPC的控制方程

(16)

式(16)给出了功率误差信号的导数与变流器交流侧调制电压之间的关系。利用式(16)可根据功率误差信号的导数直接求得变流器交流侧调制电压，驱动转子侧变换器开关管，实现基于滑模变结构的直接功率控制。图3为基于SMC-DPC的双馈电机控制策略。

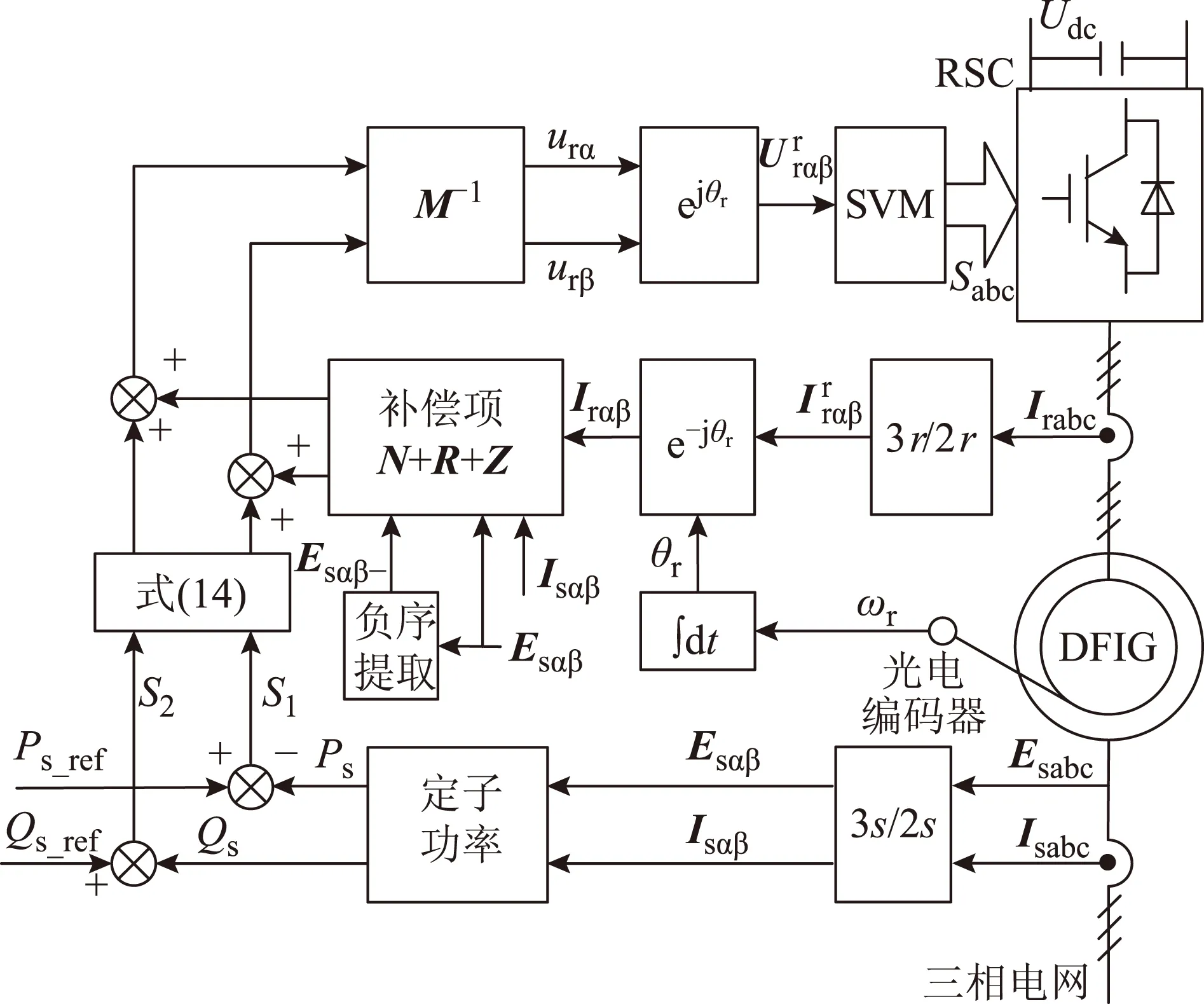
图3　基于SMC-DPC的双馈电机控制策略Fig.3　Schematic diagram of the control strategy based on SMC-DPC for RSC

2.2不平衡电网电压下的功率优化补偿方案

在电网电压不平衡条件下，并网电流的正、负序分量可分别描述为

(17)

结合式(11)中表示的电网电压的正、负序分量，可得到不平衡电网电压下有功和无功功率表达式

(esα+isβ-+esβ+isα-+esα-isβ++esβ-isα+)]

(18)

(esβ+isα--esα+isβ-+esβ-isα+-esα-isβ+)]

(19)

观察式(18)与式(19)可知，不平衡电网电压下，双馈电机输入到电网的能量除平均有功和无功功率外，还含有两倍频的有功、无功功率波动成分。

在电网电压平衡的情况下，应用2.1节提出的基于滑模变结构的控制策略，只要给定有功功率、无功功率参考值为恒定值，即可有效控制网侧变换器并网运行。但当电网不平衡时，由于负序分量引起的功率波动量的存在，使得我们不得不重新考虑功率参考量的给定，通过加入一定的补偿量，来满足双馈风电系统的并网要求。

在不考虑直流母线电压对转子侧变换器影响的情况下，根据不同运行状况下对双馈电机的控制要求，本文在不平衡电网电压条件下为转子侧变换器设定了3个控制目标：

1)目标一：保持双馈电机定子输入电网的有功功率恒定，消除有功功率二倍频波动。

在本控制目标下，式(18)中有功功率的二倍频振荡量为零，由此可得到

(20)

由式(20)可得到定子电压和电流的正、负序分量幅值与相位的关系为

(21)

此时，有功功率和无功功率给定量均为式(18)和式(19)中的平均功率值。若要求有功功率中不含二倍频振荡，则有功功率给定量只要保持为原平均功率值即可，无需进行功率补偿。而无功功率的二倍频振荡仍然存在；若不对无功功率给定值进行补偿，则会使定子输入电网的电流发生严重畸变，畸变电流会对双馈电机和电力系统产生不利影响，这也是风力发电系统并网导则所不允许的。因此，有必要对无功功率给定值进行补偿，以保证定子入网电流的正弦度。

将式(21)代入式(19)的振荡分量中，可得到如式(22)所示的无功补偿量。

Qs_comp=

(22)

2)目标二：保持定子输入电网的无功功率恒定，消除无功功率和电磁转矩中的二倍频波动。

在本控制目标下，式(19)中无功功率的二倍频振荡量为零，由此可得到

(23)

由式(23)可得到正、负序电压幅值与相位的关系为

(24)

此时，无功功率给定值为平均功率值，无需补偿。同样要保证定子入网电流的正弦度，需要对有功功率进行补偿，将式(24)代入到式(18)的功率振荡量中可得到有功功率补偿量为

Ps_comp=

(25)

3)目标三：定子输出对称、正弦的并网电流，单位功率因数并网运行。

在不平衡电网电压下，电网电流波形的不对称主要由负序电流产生，为了获得对称、正弦的入网电流，需消除入网负序电流的影响。由功率角度分析，相当于消除由负序电流产生的功率波动分量。从补偿角度看，消除功率波动成分等效于在上文有功和无功平均功率给定量基础上，均都补偿上由正序电流产生的功率波动分量。由以上分析可知，此时isα=isβ=0，计算可得有功功率和无功功率补偿量分别为

(26)

综上所述，在电网不平衡条件下，转子侧变流器的控制策略只需要在原来平衡电网电压条件下的有功或无功功率给定值的基础上，加入相应的补偿量，即可实现不同的控制目标。图4为不平衡电网电压下基于滑模变结构直接功率控制的双馈风电系统转子侧变换器控制结构。

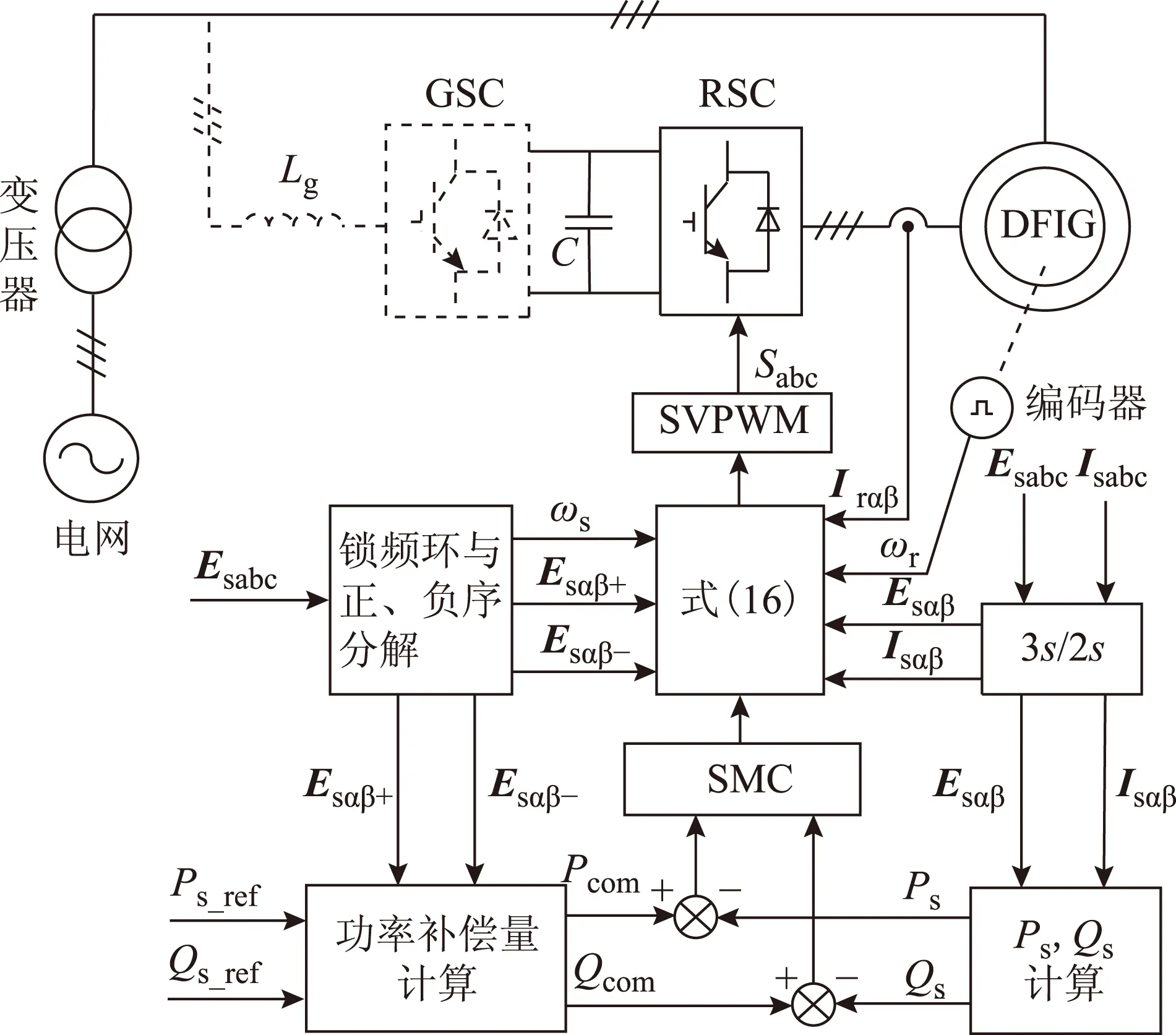
图4　基于滑模变结构控制的转子侧变换器控制结构Fig.4　Schematic diagram of the proposed control strategy based on SMC for RSC

3　仿真与实验

3.1仿真结果与分析

为了证明本文所提出的控制策略的有效性，基于Matlab/Simulink仿真软件，对一个额定容量为1.5 MW的双馈风电系统进行了仿真研究。系统仿真主要参数为(折算到定子侧后)：双馈电机额定功率1.5 MW，额定频率50 Hz，定子额定电压690 V，转子侧开路电压2 000 V，极对数为2，额定转速1 800 r/min，定转子绕组采用三角形/星形联结，定子电阻0.002 05 Ω，转子电阻0.001 82 Ω，定子自感3.99 mH，转子自感3.977 mH，互感3.915 mH，转动惯量97.5 kg·m2，直流母线电压1 200 V，变换器开关频率5 kHz。控制参数：K11=K21=10 000，K12=K22=1 000，滑模面宽度S1=S2=15 000。

由于电网故障一般持续时间很短，因此本文认为在电网发生故障期间，风力机转速不变。该仿真是在系统额定运行状态下进行的，此时双馈风机转速为1 800 r/min，输出总功率为1.5 MW，定子侧输出功率为1.25 MW。假定风电系统通过三相并网隔离变压器接入的10 kV高压电网在0.2 s发生单相接地故障，并网变压器高压侧A相在0.2 s跌落至0.8 (pu)，由于并网变压器多采用三角形/星形联结方式与三相电网相连，考虑到变压器相位变换作用，使得DFIG定子端电压产生了一个约为0.15 (pu)的两相跌落。图5为上述电网故障情况下采用3种控制目标的仿真波形。

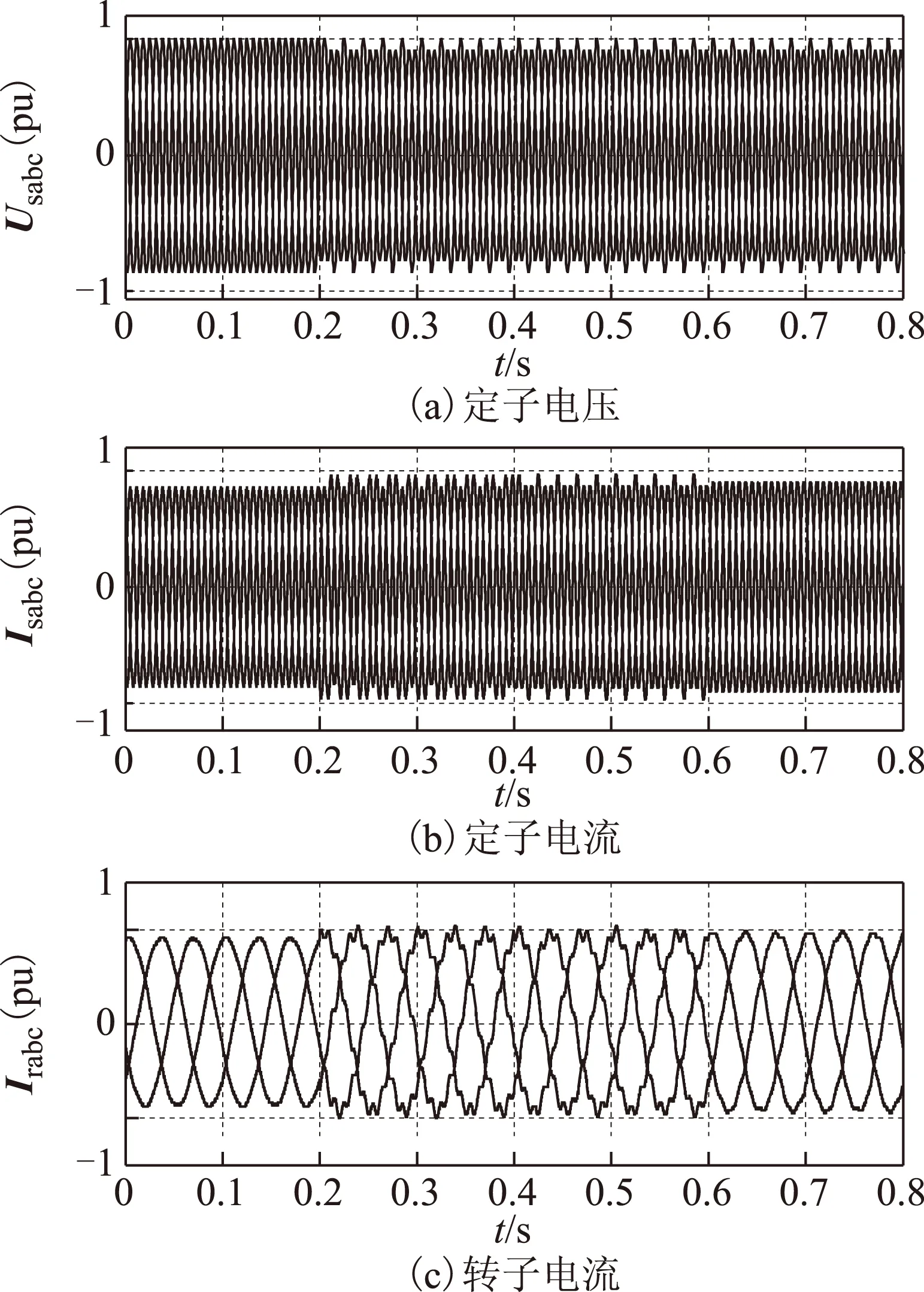
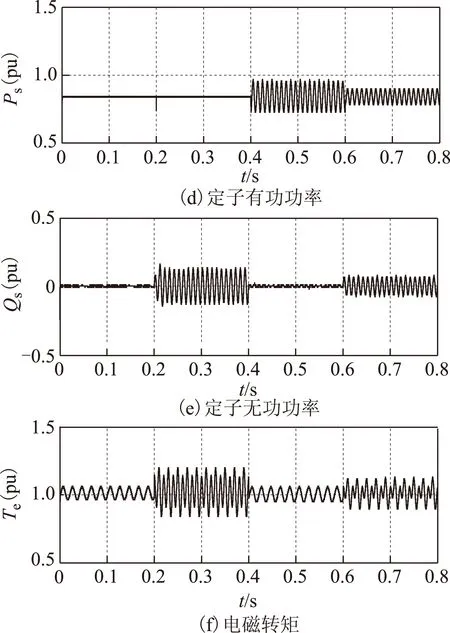
图5　不平衡电网电压下采用所提出的控制策略的仿真波形Fig.5　Simulation results using the proposed control strategy under unbalanced grid voltage conditions

在0～0.2 s期间，定子电压为三相平衡电网电压。从图5中可看出，在平衡电网电压条件下，采用所提出的转子侧变换器控制策略可以实现对双馈电机的有效控制，且控制效果良好，定、转子电流均能保持三相平衡，且波形正弦、无畸变，定子输出的有功和无功功率均保持恒定。在此值得注意的是，图5f中的电磁转矩波形存在基频振荡项，这是由双馈电机起动时电网电压瞬间变化所产生的暂态磁链直流分量引起的。由于本控制策略中并未加入相应的灭磁控制算法，这部分暂态磁链无法快速衰减，因此在较短的仿真时间内，电磁转矩的这部分基频振荡量会一直存在。

定子电压在0.2 s时发生上述的两相跌落。在0.2～0.4 s期间，采用控制目标一，保持定子输出有功功率恒定。从图5d和图5e中可知，定子输出的有功功率恒定，无功功率存在二倍频振荡。图5b中所示的定子入网电流出现三相不平衡，但波形正弦度良好，并未发生畸变。图5c中转子电流发生畸变，这主要是由定子两相静止参考坐标系下的负序电流转换到实际的转子坐标系时产生的，此时，转子正序电流频率为10 Hz，转子负序电流频率为60 Hz，故会产生畸变。图5f中的电磁转矩除含有暂态磁链产生的基频振荡成分外，还含有二倍频振荡成分。

在0.4～0.6 s期间，采用控制目标二，保持定子输出无功功率恒定，消除无功功率和电磁转矩中的二倍频振荡分量。从图5d和图5e中可知，定子输出的有功功率存在二倍频振荡，无功功率恒定。图5b中所示的定子入网电流出现三相不平衡，但波形正弦度良好，并未发生畸变。此时图5c中转子电流受60 Hz的负序电流的影响仍存在畸变。图5f中电磁转矩的二倍频振荡成分被消除，仅含有基频振荡。

在0.6～0.8 s期间，采用控制目标三，让定子输出三相平衡、正弦的并网电流，并保证单位功率因数并网运行。从图5中可知，负序电流被消除后，图5b所示的定子并网电流波形三相对称平衡，且正弦度良好，并未发生畸变。此时图5c中转子电流也未发生明显畸变。图5d和图5e中的有功和无功功率均存在二倍频振荡，但振荡幅度都有明显减小，约为前两个控制目标下的一半，这正与式(26)中表示的功率补偿关系相吻合。图5f中的电磁转矩振荡幅度也随之减小，但仍含有基频和二倍频振荡成分。

从上述对仿真结果的分析可知，采用所提出的功率优化补偿方案，可实现对3个控制目标的有效控制，所得到的结果与理论分析一致，证明了本文所提出基于SMC-DPC的功率优化补偿控制策略的正确性和有效性。

另外，值得指出的是，本文所提出的功率优化补偿算法在进行功率补偿量的计算时，使用的是功率参考给定量和定子电压正、负序分量幅值，这种补偿量计算方法，虽然算法上略显繁琐，但与文献[14]中提到的采用定子电压和电流正、负序分量来计算功率补偿量的计算方法相比，并未将系统控制量——定子电流引入到功率补偿量的计算中。在稳态特性方面，可有效降低定子电流扰动对功率补偿量的影响，提高系统功率补偿量的准确度和稳定性。在暂态响应特性方面，可消除定子电流相序分解对系统动态响应性能的影响，有利于提高系统动态响应速度，特别是在定子电流发生瞬时扰动恢复后，可明显缩短系统的动态响应时间。

3.2实验结果与分析

为了验证本文所提出的控制策略的可行性，构建了基于dSPACE实时仿真系统的双馈风电系统实验平台，并利用可编程交流电源模拟了变流器运行所需不平衡电网，其系统结构如图6所示。

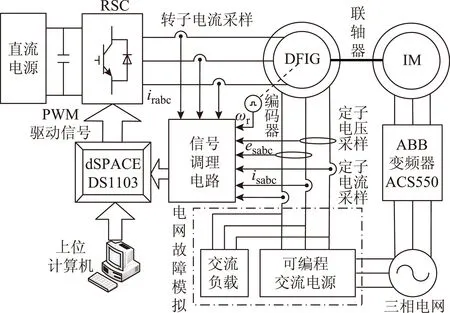
图6　基于dSPACE实时仿真系统的实验平台结构Fig.6　Schematic diagram of the experimental system based on dSPACE realtime simulation system

实验平台主要由变频调速感应电机、双馈电机及转子侧变换器三部分组成。变频调速感应电机由变频器驱动来模拟风轮机，双馈发电机定子侧接可编程交流电源，转子侧接变换器。为了通过可编程交流电源实现对电网故障的模拟，在双馈电机与可编程电源之间并有一个三相交流负载，系统工作时，双馈电机和可编程交流电源的能量都将流入这个负载，但此时双馈电机定子侧电压会与交流电源输出电压一致，这样就可以通过可编程交流电源与三相交流负载来实现对各类电网电压跌落情况的模拟，其效果与实际电网故障基本一致。最后，系统通过转接电路板与dSPACE实时仿真系统相连，实现整套系统的控制及实时状态采集。图7为所使用的实验平台的照片。

图7　基于dSPACE实时仿真系统的变流器实验平台Fig.7　Experimental system based on dSPACE realtime simulation system

实验平台所用双馈电机的主要参数为：额定功率 为10 kW，额定频率为50 Hz，极对数为3，同步转速为1 000 r/min，定转子绕组均采用Y形联结，定子电阻为0.5 Ω，转子电阻(折算后)为0.595 Ω，定子自感为74.5 mH，转子自感(折算后)为76.5 mH，互感为72.4 mH，转子转动惯量为0.131 kg·m2。

实验功率2.5 kW，电机运行在亚同步状态，转速800 r/min，转差率0.2，通过可编程交流电源输入到定子线电压有效值为180 V，直流母线电压为350 V，直流母线电容为470 μF，开关频率为20 kHz。

图8为平衡电网电压下的定子相电压波形，为了模拟与仿真中所提到的同样类型的故障，双馈电机在正常并网运行后，使用可编程交流源，让B、C两相电压产生跌落，跌落值约为20 V，A相不变，此时不平衡度约为6%。

图8　平衡电网电压条件下定子相电压波形Fig.8　Stator phase voltage waveform under balanced grid voltage conditions

图9为不平衡电网电压条件下的定子相电压波形。

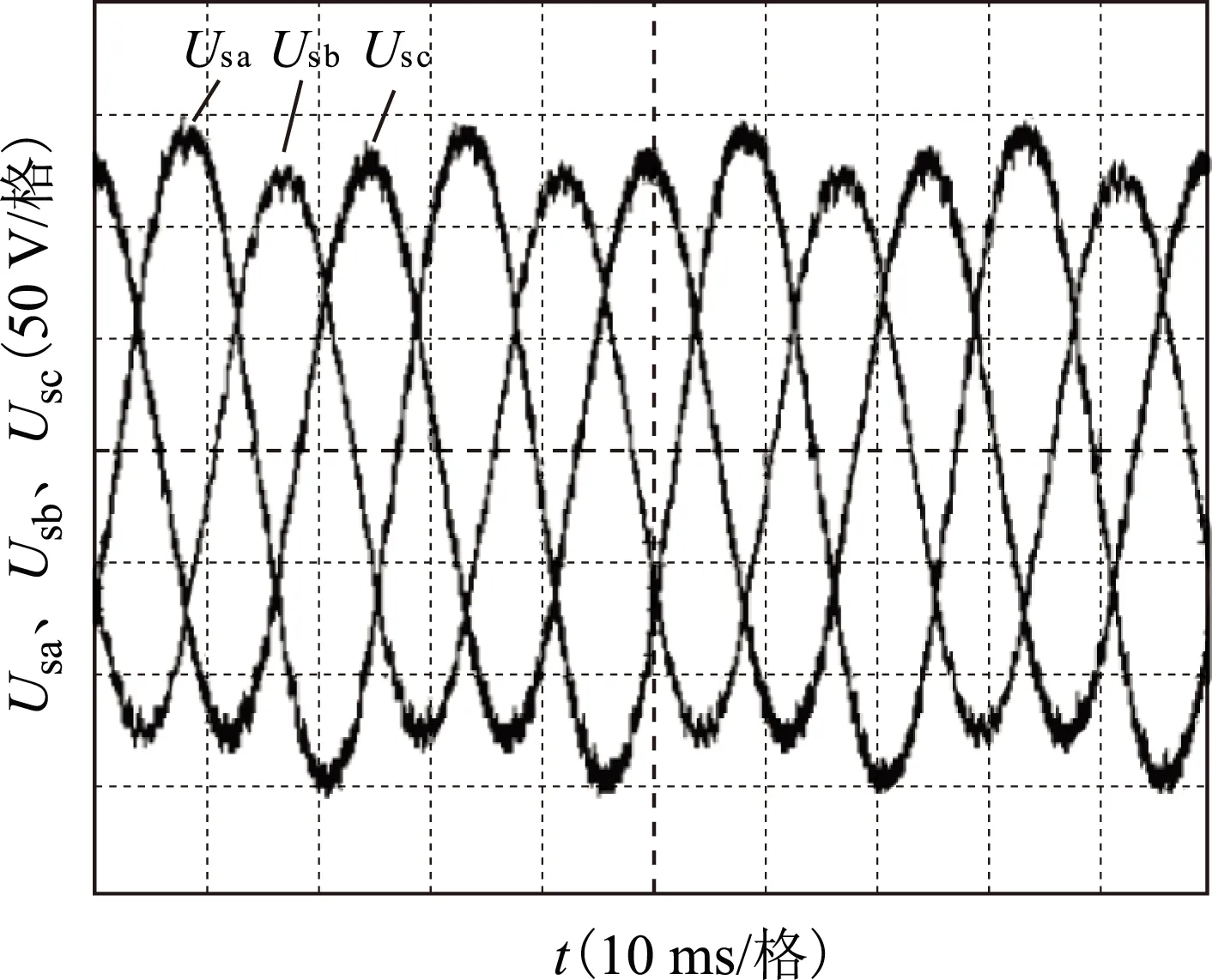
图9　不平衡电网电压条件下定子相电压波形Fig.9　Stator phase voltage waveform under unbalanced grid voltage conditions

图10为平衡电网电压以及上述不平衡电网电压下，采用本文所提出的控制策略得到的实验波形。

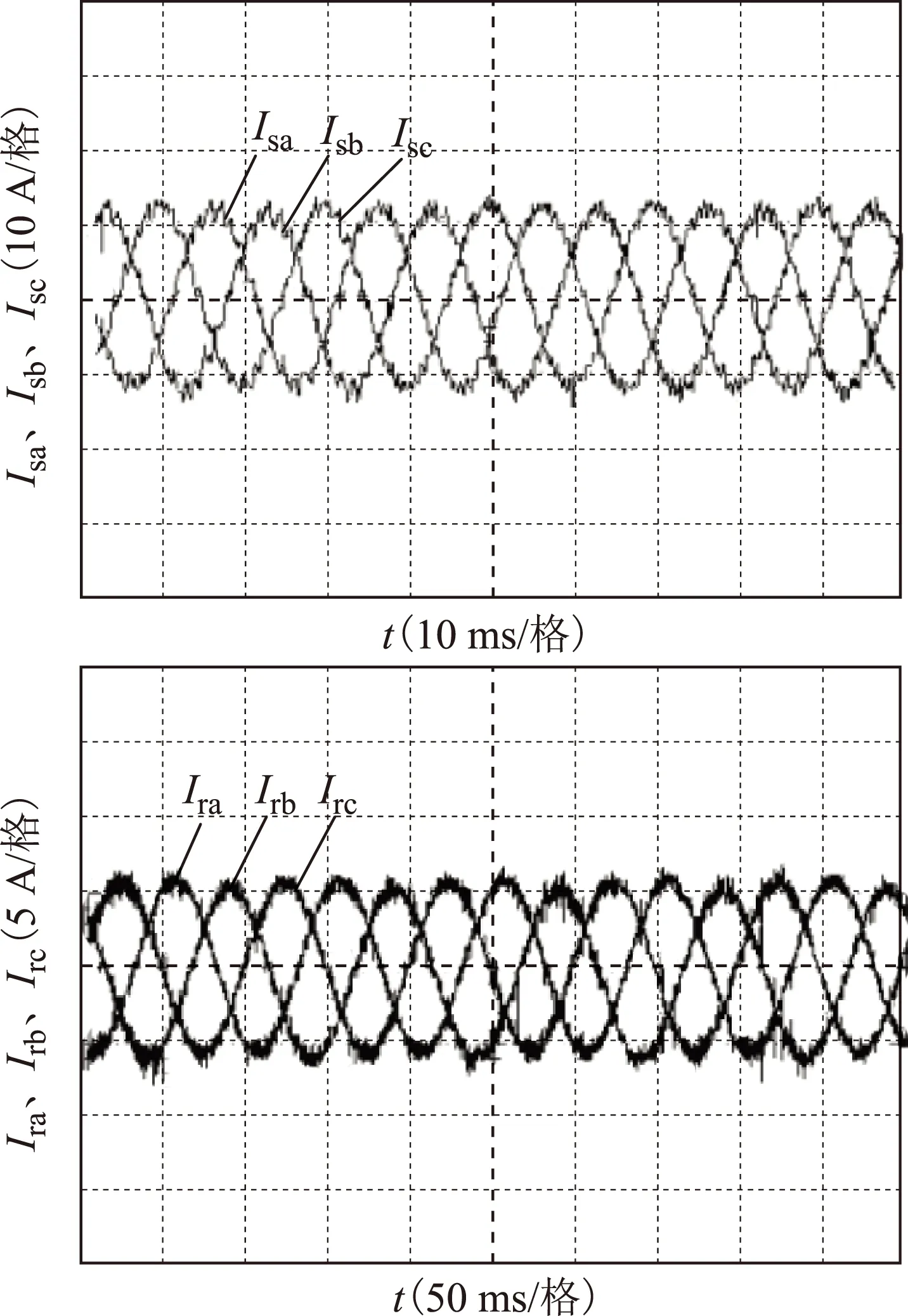
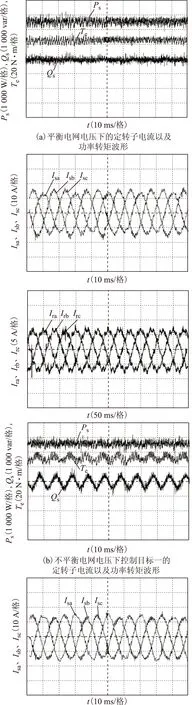
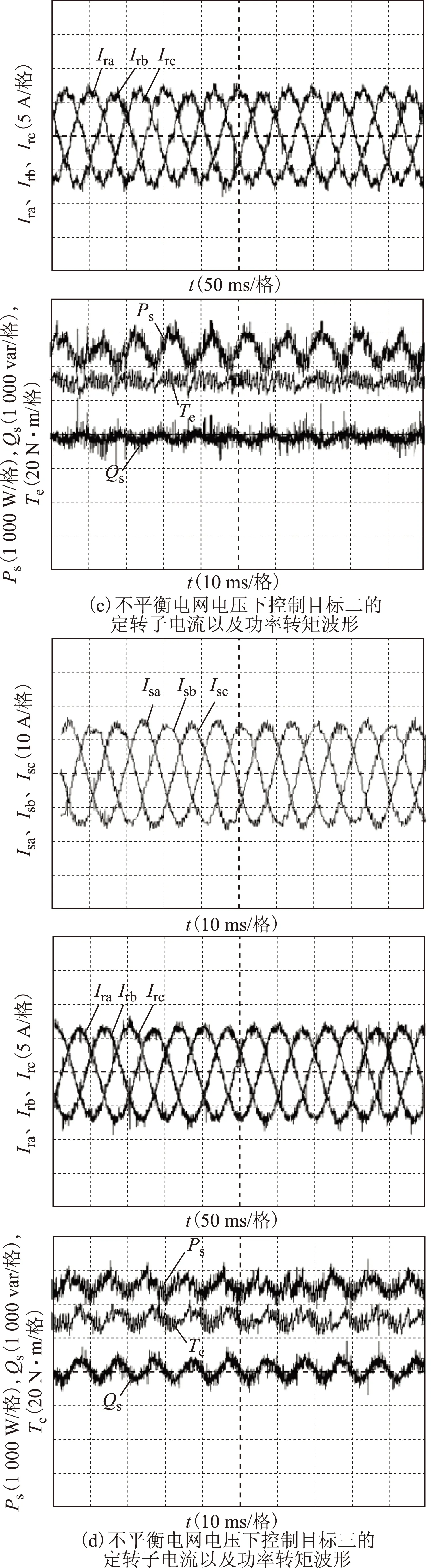
图10　采用所提出的控制策略的实验波形Fig.10　Experimental results using the proposed control strategy

图10a为平衡电网电压条件下采用本文所给出的基于SMC-DPC的控制策略所得到的实验波形。从图中可以看出，在平衡电网电压下，采用上述控制策略，双馈电机输出的有功和无功功率均能得到有效控制，定、转子电流波形均能保持正弦，无明显畸变。同时由于实验所采用的双馈电机定子电阻较大，且实际控制效果并没有仿真中那么理想，难免在定子中出现暂态电流，且实验中电压跌落较小。因此，定子的暂态磁链在实验中已经被衰减掉，图中电磁转矩并未出现仿真中的基频振荡。

图10b为不平衡电网电压条件下，采用有功功率恒定的控制目标所得到的实验波形。从图中可以看出有功功率恒定，无功功率和电磁转矩都存在明显的二倍频波动；定子电流出现三相不平衡，B、C相电流明显高于A相电流，但正弦度良好；转子电流由于负序分量的存在发生畸变。

图10c为不平衡电网电压条件下，采用无功功率恒定、消除转矩二倍频波动的控制目标所得到的实验波形。从图中可看出无功功率基本恒定，电磁转矩也未出现明显的二倍频波动，有功功率存在二倍频波动；定子电流不对称正弦，A相电流明显高于B、C相电流；转子电流同样存在明显畸变。

图10d为不平衡电网电压条件下，采用定子电流对称的控制目标所得到的实验波形。从图中可以看出，有功、无功功率以及电磁转矩均存在二倍频波动，但波动幅度比前两种控制目标下的幅度明显减小；定子电流对称正弦，转子电流波形无明显畸变，正弦度明显优于前两种控制目标下的波形。

从上述实验结果分析可知，采用所提出的控制策略可实现对本文中3个控制目标的有效控制，所得到的实验结果与理论分析一致，由此可知本文所提出的控制策略是可行的。

4　结论

在两相静止坐标系下，建立了基于功率控制的双馈电机统一的数学模型，采用基于滑模变结构的直接功率控制方法实现了对双馈风电系统转子侧变换器的有效控制。在不平衡电网电压下，提出了一种新型的功率优化补偿控制策略。该控制策略无需对定子电流进行相序分解，简化了系统控制结构，同时，改进后的功率补偿量计算方法有效降低了定子电流扰动对功率补偿量的影响，提高了系统功率补偿量的准确度和稳定性。仿真和实验结果均证明了本文所提出的控制策略的正确性和可行性。采用本文所提出的控制策略可有效改善双馈电机在不平衡电网电压条件下的运行品质，提高双馈风电系统对电网扰动和故障的适应能力。

[1]Li H，Chen Z.Overview of different wind generator systems and their comparisons[J].IET Renewable Power Generation，2008，2(2)：123-138.

[2]Pena R，Cardenas R，Alepuz G，et al.Overview of control systems for the operation of DFIGs in wind energy applications[J].IEEE Transactions on Industrial Electronics，2013，60(7)：2776-2798.

[3]赵霞，王倩，邵彬，等.双馈感应风力发电系统低电压穿越控制策略研究及其分析[J].电力系统保护与控制，2015，43(16)：57-64.

Zhao Xia，Wang Qian，Shao Bin，et al.Low voltage ride through control strategy and its analysis of doubly fed induction generator generator[J].Power System Protection and Control，2015,43(16)：57-64.

[4]贺益康，胡家兵，徐烈.并网双馈异步风力发电机运行控制[M].北京：中国电力出版社，2012.

[5]Hu Jiabing，He Yikang，Xu Lie，et al.Improved control of DFIG systems during network unbalance using PI-R current regulators[J].IEEE Transactions on Industrial Electronics，2009，56(2)：439-451.

[6]叶虹志，姜燕，黄守道，等.电压型PWM整流器无差拍预测直接功率控制[J].电工技术学报，2015，30(4)：121-128.

Ye Hongzhi，Jiang Yan，Huang Shoudao，et al.Deadbeat predictive direct power control for three-phase voltage source PWM rectifiers[J].Transactions of China Electrotechnical Society，2015，30(4)：121-128.

[7]周小杰，张霞，汪飞.基于功率变化子空间的直接功率控制[J].电工技术学报，2015，30(24)：142-151.

Zhou Xiaojie，Zhang Xia，Wang Fei.Direct power control based on subspace of power variation[J].Transactions of China Electrotechnical Society，2015，30(24)：142-151.

[8]郭三明，孙鹏荆，敬树仁，等.基于预测模型的STATCOM功率控制策略建模与仿真[J].电力系统保护与控制，2015，43(1)：88-92.

Guo Sanming，Sun Pengjing，Jing Shuren，et al.Research on modeling and simulation of power control method for STATCOM based on predictive model[J].Power System Protection and Control，2015,43(1)：88-92.

[9]Abad G，Rodriguez M A，Iwanski G，et al.Direct power control of doubly-fed-induction-generator-based wind turbines under unbalanced grid voltage[J].IEEE Transactions on Power Electronics，2010，25(2)：442-452.

[10]Hu Jiabing，Nian Heng，Hu Bin，et al.Direct active and reactive power regulation of DFIG using sliding-mode control approach[J].IEEE Transactions on Energy Conversion，2010，25(4)：1028-1039.

[11]Nian Heng，Song Yipeng，Zhou Peng，et al.Improved direct power control of a wind turbine driven doubly fed induction generator during transient grid voltage unbalance[J].IEEE Transactions on Energy Conversion，2011，26(3)：976-986.

[12]Martinez M I，Tapia G，Susperregui A，et al.Sliding-mode control for DFIG rotor-and grid-side converters under unbalanced and harmonically distorted grid voltage[J].IEEE Transactions on Energy Conversion，2012，27(2)：328-338.

[13]Martinez M I，Susperregui A，Tapia G，et al.Sliding-mode control of a wind turbine-driven double-fed induction generator under non-ideal grid voltages[J].IET Renewable Power Generation，2013，7(4)：370-379.

[14]Shang Lei，Hu Jiabing.Sliding-mode-based direct power control of grid-connected wind-turbine-driven doubly fed induction generators under unbalanced grid voltage conditions[J].IEEE Transactions on Energy Conversion，2012，27(2)：362-373.

[15]张迪，魏艳君，马利轩，等.不平衡电网电压下基于滑模变结构控制的双馈风电系统网侧变流器控制策略[J].电工技术学报，2015，30(10)：266-275.

Zhang Di，Wei Yanjun，Ma Lixuan，et al.Sliding-mode control for grid-side converters of DFIG-based wind-power generation system under unbalanced grid voltage conditions[J].Transactions of China Electrotechnical Society，2015，30(10)：266-275.

Sliding-Mode Control for Rotor-Side Converters of DFIG-Based Wind-Power Generation System Under Unbalanced Grid Voltage Conditions

Zhang DiWei YanjunYang ZongfengDing HaoQi Hanhong

(School of Electrical EngineeringYanshan UniversityQinhuangdao066004China)

A general mathematical model for the double fed induction generator (DFIG) is presented based on power control in the two-phase static coordinate，which is suitable for either balanced or unbalanced grid voltage condition.Direct power control based on sliding-mode control is used to realize the control of DFIG’s rotor-side converter.The controller has advantages of simple structure，rapid response，and high robustness.A novel optimization control strategy is proposed for compensating power under unbalanced grid voltage conditions.The proposed control strategy is implemented by directly increasing power compensation to the power reference value，which eliminates the sequence component extraction of the stator and rotor currents.Therefore the control structure is simplified.More importantly，the proposed control algorithm can reduce the influence of the stator current disturbance on the power compensation，thus improves system robustness.Simulation and experiment results confirm the reliability and validity of the proposed control strategy.

Doubly-fed wind generator (DFIG)，rotor-side converters，sliding-mode control，direct power control，unbalanced grid voltage

2015-07-14改稿日期2016-01-19

TM46

张迪男，1986年生，博士，研究方向为双馈并网风力发电系统及其控制技术。

E-mail：dzhang1120@ysu.edu.cn

漆汉宏男，1968年生，教授，博士生导师，研究方向为新能源发电与功率变换技术。

E-mail：hhqi@ysu.edu.cn (通信作者)

河北省应用基础研究计划重点基础研究项目(13964304D)和教育部高等学校博士学科点专项科研基金(20121333110007)资助。