三维重建表面几何特征的提取与参数测量计算

郭盛威，章秀华，范　艳，邓哲煜

武汉工程大学机电工程学院，湖北 武汉 430205

三维重建表面几何特征的提取与参数测量计算

郭盛威，章秀华*，范艳，邓哲煜

武汉工程大学机电工程学院，湖北 武汉 430205

对三维重建结果的表面特征进行提取和误差分析，是提高三维目标测量精度的关键步骤.提出了对三维重建表面几何特征进行提取，并对其进行参数测量计算的方法.首先利用STL文件对三维重建得到的目标点云数据进行读取、导出并筛选，得到三维重建目标的点云数据，通过迭代计算生成CAD模型表面点云数据.再提取重建目标与CAD模型的几何特征，计算粗糙度、平行度和平面度等几何参数特征值，进行误差比较和分析，最后将该结果反馈至三维目标重建过程中.实验结果表明，提出的方法能有效地提取三维重建结果表面几何特征及对表面进行测量计算.

三维重建；表面特征提取；表面拟合；误差分析

1　引言

物体三维重建是对三维物体建立适合计算机表示和处理的模型［1］，是在计算机环境下对三维物体进行处理和分析其性质的基础［2］，也是在计算机中建立表达客观世界的虚拟现实的关键技术［3］.

计算机内生成三维物体主要由两种方法实现.一种是使用几何建模软件，在人为控制下生成三维几何模型，另一种则是通过三维重建，利用物体的二维投影重建出物体的三维信息等［4］.经过三维重建得到一组三维点云数据，三维点云数据在逆向工程、工程检测、自主导航、文物保护、虚拟现实等领域的应用中，发挥着至关重要的作用［5］.因此，研究三维点云数据的几何特征的提取与误差分析是评判三维重建效果的关键技术，对于改善三维重建的算法与应用具有重要的意义.

利用三维图像分析，从三维细化的结果中，可以获得三维物体的很多特征信息，包括物体的形状结构、连接与拓扑关系以及物体的轴线基准、轴线长度等，它们反映了三维物体的一些基本结构性质和基准线、基准面等特征.三维细化处理完成后，进一步根据三维重建图像数据和三维细化后提供的基准信息，计算表面积和表面曲率以及各种形状和位置尺寸［6-8］.

2　表面几何参数的提取与计算

2.1读取重建物体与物体的CAD模型所有点坐标

参数提取过程以CATIA作为软件基础，以Excel为辅助.在参数提取过程中，主要使用CATIA调整重建物体的形状、位置，并输出得到点云数据.基本过程为：在CATIA中新建一个点群造型编辑，将待比较的重建物体与物体CAD模型的STL文件分别导入，重建结果坐标原点与定义的原点不一致，修改重建物体坐标与大小，使重建物体坐标与CAD模型坐标一致，导出各点坐标并存储于Excel表格中.

重建物体中包含的点个数相对于CAD模型来说，数据量非常大，比较起来不仅非常复杂，而且对计算机要求很高.如果对物体中每个面都进行比较，工作量很大，而且具有盲目性，是不切合实际的.为了提高工作效率，让分析处理方法更快更稳定的在各种计算机上运行，将待比较的面提取出来，分别进行比较.

2.2提取待比较平面

从CATIA中导出的Excel表格中包含了所有点的坐标，如何将所需面的点云数据筛选出来也是一个必须解决的问题.由于重建物体不规则，不能清楚的知道平面所在的范围，用MATLAB显示所有点，选出平面大致范围，利用迭代法的思路，多次筛选并显示，最后得到所需点云数据.

2.3拟合CAD模型对应面

CAD模型经导出的STL文件仅有特征顶点，不能直接与重建面进行比较，要对模型面进行拟合.拟合是将已知某函数的若干离散函数值｛f1，f2，…，fn｝，通过调整函数中若干待定系数f（λ1， λ2，…，λn），使得该函数与已知点集的差别（最小二乘法意义上的）最小，即将平面上一系列的点，用一条光滑的曲线连接起来.因为这条曲线有无数种可能，从而有各种拟合方法.拟合出的曲线一般可以用函数表示［9］.

拟合以及插值还有逼近是数值分析的三大基础工具，通俗意义上它们的区别在于：拟合是已知点列，从整体上靠近它们，插值是已知点列并且完全经过点列；逼近是已知曲线，或者点列，通过逼近使得构造的函数无限靠近它们.将通过拟合的对应面，与待比较面进行分析比较，求出表面几何特征参数［10-11］.

2.4误差分析

求出对应点坐标，对平面进行误差分析以及平面评估.此处选择计算表面粗糙度、变化量标准差、表面平面度和平行度来进行评估.

粗糙度是反映数据集中趋势的一项指标.其计算公式为

标准差为方差的算术平方根，反映组内个体间的离散程度.其公式为

平面度误差是指被测实际表面对其理想平面的变动量.平面度误差是将被测实际表面与理想平面进行比较，两者之间的线值距离即为平面度误差值；或通过测量实际表面上若干点的相对高度差，再换算以线值表示的平面度误差值.其公式为

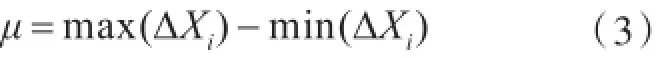
平行度是两平面或者两直线的平行程度，一平面相对于另一平面平行的误差最大值.为了区分平面度与平行度，定义平面度取20%最大与最小值的差的均值.其公式为

式（1）～（4）中，ΔXi表示待比较方向上重建物体与CAD模型的坐标变化量；Xi表示重建物体待比较方向上的坐标值；Xˉ表示重建物体待比较方向上的坐标的平均值；n表示所提取面所有点个数.通过平均值和标准差，可以计算误差值的集中趋势和离散程度.通过平面度，可以计算平面的最大误差值.

3　结果与讨论

3.1导出重建物体与物体的CAD模型所有点坐标

将重建物体与物体的CAD三维模型的STL文件分别打开并导入，存储于表格.将三维物体的各点显示出来，发现重建结果的坐标原点与定义的原点不一致［如图1（a）］，把重建物体图平移并旋转到定义的坐标系中［如图1（b）］，将文件点坐标导出，得到所需坐标.

图1　重建物体空间位置（a）与坐标变换后的位置（b）Fig.1　Reconstructed object spaceand（a）and position ofcoordinate transformation（b）

3.2提取待比较平面

导出的表格中包含所有点的坐标值，通过数据筛选将所需面的点云坐标筛选出来.通过软件显示并选取出所需的范围.将物体的CAD三维模型面编号［如图2（a）］，以1号面为例，从重建物体［如图2（b）］中提取出1号面.选取1号面4个顶点，筛选出所需平面，得到物体的CAD三维模型［如图3（a）］与重建物体［如图3（b）］的1号面各点坐标.

图2　物体的CAD三维模型图（a），三维重建结果（b）Fig.2　CAD（a）and reconstruction（b）model of the object

图3　CAD模型（a）和三维重建模型（b）的1、2、5号面Fig.3　No.1，2 and5 surfaces ofcAD model（a）and 3D reconstruction（b）

3.3拟合CAD模型对应面

物体的CAD三维模型导出的STL文件仅有特征顶点，将待比较平面进行拟合并求出平面方程.输入1号面上三点坐标，求出过三点坐标的平面方程，再通过该平面方程，求出物体的CAD三维模型1号面上与重建物体1号面上的对应点坐标，进行比较.

3.4误差分析

对重建物体与物体的CAD三维模型对应的5个面进行了误差分析，分别得出并记录各个面的表面粗糙度、变化量标准差、表面平面度和平行度，如表1所示.

表1　重建物体表面参数评价数据Tab.1　Evaluation of the surface parameters of the reconstruction object

通过表1中的各组数据，可以看出重建的5个面中，2号面的平面度最好，5号面的粗糙度最小，较为光滑，并与模型的5号面平行效果更好.这些数据可以反馈到三维重建过程中，用于改善三维重建效果.

4　结　语

本研究实现了三维重建结果表面特征的提取与误差分析.将重建物体与实际物体的CAD模型的表面进行比较，通过分析粗糙度、平面度、平行度等参数，得出了便于评判重建效果的数据，为后续对三维重建算法的优化改进提供了参考数据.

［1］DORAIc，JAIN A，WENG J.Optimal registration of object views using rangedata，IEEE Trans［J］.Pattern analysis and machine intelligence，1997，19（10）：1131-1138.

［2］高剑.三维重建应用系统研究［D］.济南：山东大学，2009.

［3］ROBERT A，SACHS E，STOOPSd.3-Draw：A tool fordesigning 3D shapes［J］.IEEEcomputer graphics and applications，1991，11（6），18-26.

［4］洪汉玉.现代图像图形处理与分析［M］.武汉：中国地质大学出版社，2011.

［5］薛耀红.点云数据配准及曲面细分技术研究［D］.长春：吉林大学，2010.

［6］HONG H Y，ZHANG T X.Fast restoration approach for rotational motion blurred image based ondeconvolution along the blurring paths［J］.Optical engineering，2003，42（12）：3471-3486.

［7］洪汉玉，王进，张天序，等.红外目标图像循环迭代复原算法的加速技术研究［J］.红外与毫米波学报，2008，27（2）：115-118.

HONG H Y，WANG J，ZHANG T X，et al.Study on acceleration technique ofcirculation iterative restoration algorithm for infrared target images［J］.Journal of infrared and millimeter waves，2008，27（2）：115-118.

［8］洪汉玉，张天序，余国亮.航天湍流退化图像的极大似然估计规整化复原算法［J］.红外与毫米波学报，2005，24（2）：130-134.

HONG H Y，ZHANG T X，YU G L.Regularized restoration algorithm of astronautcal turbulence-degraded images using maximum-likelihood estimation［J］.Journal of infrared and millimeter waves，2005，24（2）：130-134.

［9］李二涛，张国煊，曾虹.基于最小二乘的曲面拟合算法研究［J］.杭州电子科技大学学报，2009，29（2）：48-51.

LI E T，ZHANG G X，ZENG H.Algorithm of surface fitting research based on least-squares methods［J］. Journal of Hangzhoudianzi university，2009，29（2）：48-51.

［10］彭芳瑜，周云飞，周济.基于插值与逼近的复杂曲面拟合［J］.工程图学学报，2002（4）：87-96.

PENG F Y，ZHOU Y F，ZHOU J.Algorithm of sculptured surface fitting based on interpolation and approximation［J］.Journal of engineering graplis，2002（4）：87-96.

［11］任同群，赵悦含，龚春忠，等.自由曲面测量的三维散乱点云无约束配准［J］.光学精密工程，2013，21（5）：1234-1243.

REN T Q，ZHAO Y H，GONGc Z，et al.Unconstrained registration of 3-D scattered pointclouds for free-form shape measurement［J］.Optics and precision engineering，2013，21（5）：1234-1243.

本文编辑：陈小平

Extracting Geometric Features andcalculating Parameters for Three-Dimensional Reconstruction Surface

GUO Shengwei，ZHANG Xiuhua，FAN Yan，DENG Zheyu
School of Mechanical and Electrical Engineering，Wuhan Institute of Technology，Wuhan 430205，China

Extraction of surface feature and error analysis is an important step for accurate measurement of threedimensional（3D）reconstruction.A method for extracting the surface feature andcomputing the parameter of 3D reconstruction was proposed.Here we used the STL file to extract and import the pointclouddata for the 3D reconstructed object，thus we obtained the pointclouddata of 3D reconstructed object，and generated pointclouddata of thecomputer aideddesigncAD model surface by iteration.Then we extracted the geometric features of the reconstructed object and thecAD model，andcomputed the feature values of geometric parameter such as roughness，parallelism and flatness tocompare and analyze the errors.Finally，the result was fed back to the processing of 3D reconstruction.Itdemonstrates that the proposed algorithm has good effects in extracting surface feature and analyzing the errors of 3D reconstruction.

reconstruction；surface feature extraction；surface fitting；error analysis

TP391

A

10.3969/j.issn.1674-2869.2016.02.015

1674-2869（2016）02-0185-04

2016-01-26

国家自然科学基金面上项目（61175013）；湖北省自然科学基金创新群体项目（2012FFA046）；武汉市国际科技合作计划项目（2014030709020310）

郭盛威，硕士研究生.E-mail：393781957@qq.com

章秀华，博士，副教授.E-mail：amyyzxh@sina.com