基于FLAC3D大冶铁矿矿柱回采过程的应力分析

周德红，李　文，冯　豪，王浩然

武汉工程大学资源与土木工程学院，湖北 武汉 430074

基于FLAC3D大冶铁矿矿柱回采过程的应力分析

周德红，李文，冯豪，王浩然

武汉工程大学资源与土木工程学院，湖北 武汉 430074

为了增加资源回收率，金属非金属矿山在回采后期需要对残留矿柱进行二次回采.矿柱结构破坏必然引发采场力学状态发生变化，甚至影响整个采空区的稳定性.以大冶铁矿矿柱回采过程为例，选用动力有限元法分析其采空区动力扰动下的响应特征及应力分布规律.选取直径3 m、高12 m的竖直圆形矿柱采用FLAC3D（Fast Lagrangian Analysis of Continua）对矿柱应力随时间变化情况进行数值模拟分析.模拟分析结果表明，矿柱负载分别在20 MPa，40 MPa的情况下，动力扰动对矿柱的影响随其负载的增大越来越明显，在动力扰动下矿柱越容易导致失稳破坏.矿柱的负载越小，整个采场的稳定性、安全性也就越好，因此，在为矿柱回采进行充填设计时，应充分考虑矿柱的负载作用.

矿柱；应力；FLAC3D；采空区

2　模型的建立

2.1工程概况

大冶铁矿位于湖北省黄石市铁山区.大冶铁矿为低山-丘陵组成的山丘-盆地地形，山脉走向NWW，与构造线走向一致.地势北高南低，低山与丘陵之间走向为NWW-SEE.铁门坎采区浅部矿体于1984年7月结束露天开采，坑底标高-36 m. -36 m以下及挂帮矿转为地下开采.该矿区地下开采工程由长沙黑色冶金矿山设计院设计，阶段高60 m，分段高12 m，采矿方法为无底柱分段崩落法开采.该采区基建工程于1995年竣工投产.到2005年底，-62 m分段及以上分段已由大冶铁矿井下车间采用无底柱分段崩落法开采完毕.

各区段分层矿柱统计：其中-62 m到-50 m区段由于充填有大量黄泥，为防止-62 m分段的黄泥下泄影响下分段的采矿，对-62 m分段底柱与点柱不予开采，故不作统计.各分段统计矿柱如表1所示.由表1可知，铁门坎采区-50 m到-110 m区段，顶底柱占比84.5%，点柱占比15.5%，也就是说残留矿柱主要是顶底柱；残留矿柱约77 677 m3，矿石体质量按4.12 t/m3计算，资源储量32.0万吨.从安全回采来看，-110 m分段底柱列入下区段回收较妥，故本区段可回收矿柱约63 217 m3，资源储量为26.0万吨.

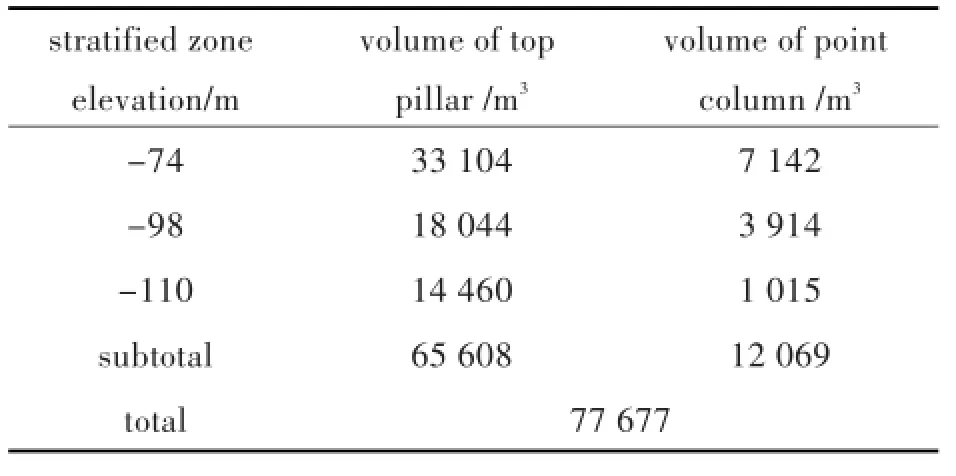
表1　矿柱统计表Tab.1　Pillar statistics table

2.2数值模型网格的建立

围岩和矿体物理力学参数根据前人研究的大冶铁矿岩体物理力学参数选取［4-9］，结合工程实践经验，各计算参数取值见表2.

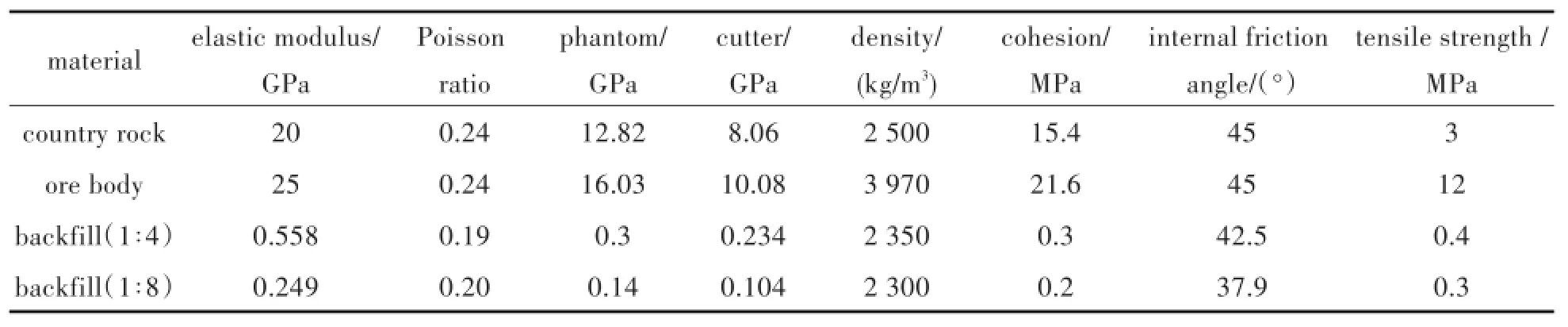
表2　材料物理力学参数Tab.2　Material physical and mechanical parameters

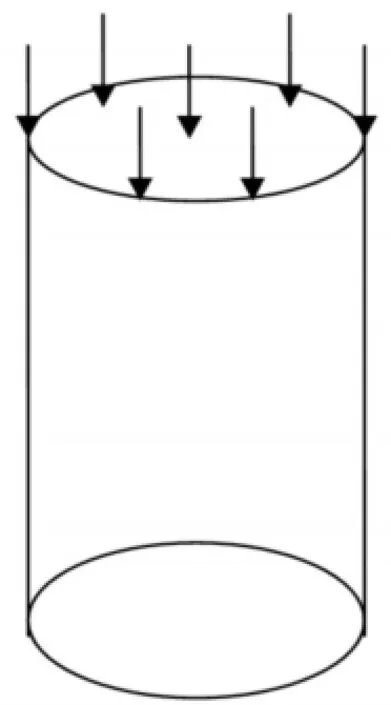
图1　矿柱静力模型Fig.1　Pillar static model

选取矿柱直径3 m、高12 m的竖直圆形矿柱进行计算模拟分析.为了模拟竖直方向的地应力，模型上边界施加一竖直方向的静载（负荷），下边界施加位移约束.为考察动力扰动对矿柱的影响，在模型上边界施加动力荷载.矿柱的静力模型、动力模型、计算网格见图1、图2和图3.

3　模拟结果及分析

3.1设计计算方案

首先，为了考察矿柱的承载能力，计算当高径比为4∶1时，矿柱在不同静压力下的应力和变形情况.基于此，为了进行动力扰动分析，在矿柱模型顶端施加应力波荷载.选用正弦脉冲来分布荷载（见图4）.当扰动应力波的峰值分别取pmax= 10 MPa、30 MPa时，分析计算静载大小对矿柱的影响.

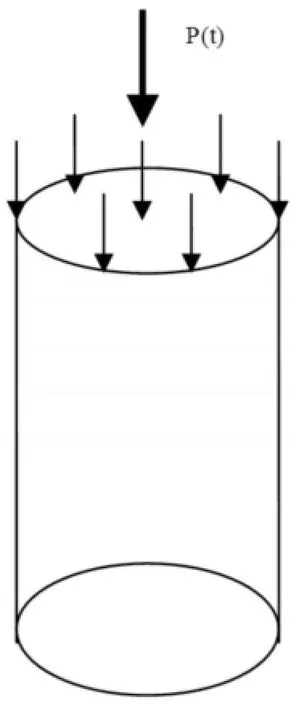
图2　矿柱动力模型Fig.2　Pillar dynamic model

图3　数值模拟网格划分模型Fig.3　Meshing model of numerical simulation

3.2矿柱应力荷载模拟分析

根据工程地质，利用FLAC3D程序强大的后处理功能［10-15］，对大冶铁矿矿柱回采过程进行安全性分析，限于篇幅，这里只给出矿柱动力模拟分布图.

分别取矿柱模型高0 m、6 m和12 m处横截面中心点作为动态信息记录对象，以研究应力波作用对矿柱的应力变化.在时间变化时，负载为pmax= 10 MPa、30 MPa时最大主应力的变化情况见图5～图16.

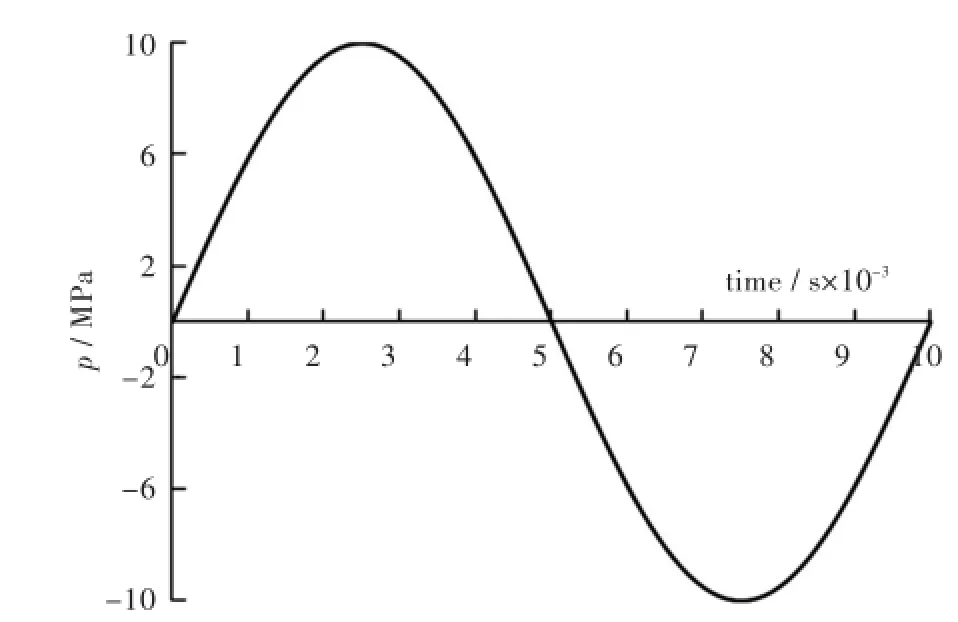
图4　应力波时程曲线Fig.4　Time curve of stress wave

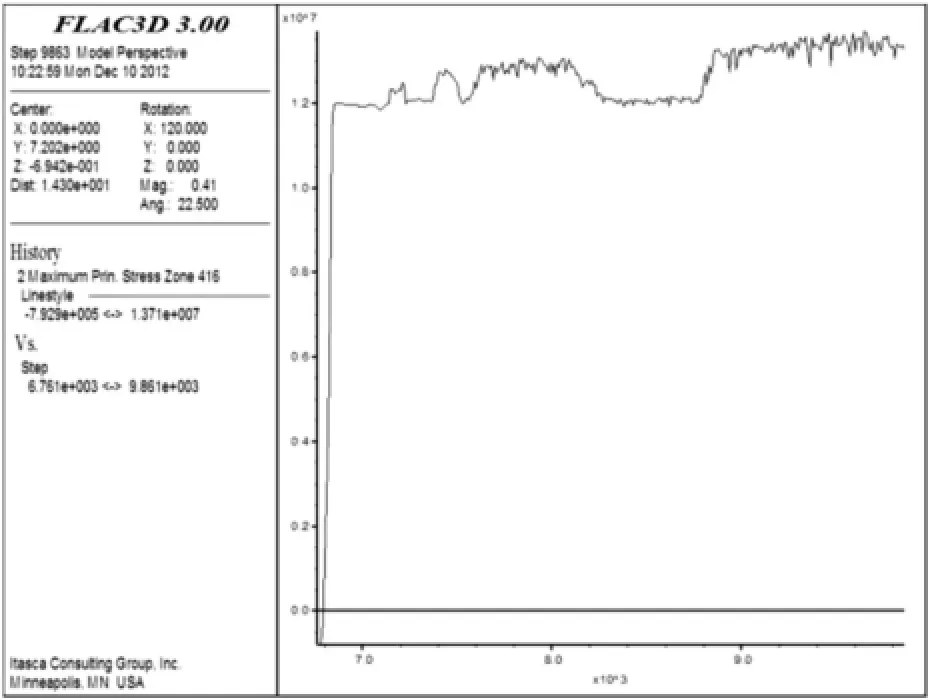
图5　p=20 MPa、pmax=10 MPa、z=0 m时最大主应力时程曲线Fig.5　Time curve of maximum principal stress at p=20 MPa，pmax=10 MPa and z=0 m

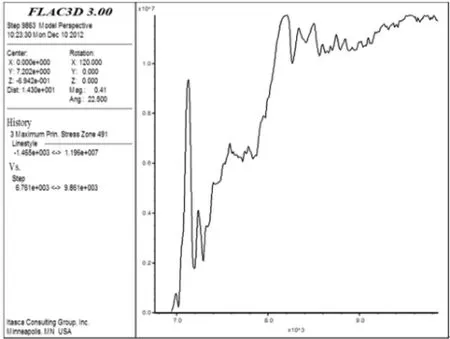
图6　p=20 MPa、pmax=10 MPa、z=6 m时最大主应力时程曲线Fig.6　Time curve of maximum principal stress atp=20 MPa，pmax=10 MPa and z=6 m

模拟过程显示，模型单元最大主应力在负载p=20 MPa、应力波峰值pmax=10 MPa时曲线如图5、图6和图7所示；主应力时程曲线在应力波峰值pmax=30 MPa时如图8、图9和图10所示.对比表明，模型上部单元的应力在应力波作用后变化较为稳定，模型中部和下部单元的应力变化有少许波动；随着应力波峰值的增大，矿柱模型单元的最大主应力变化不明显.

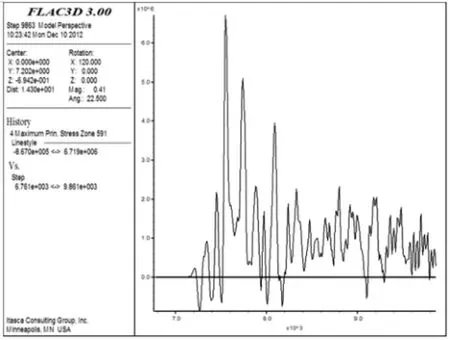
图7　p=20 MPa、pmax=10 MPa、z=12 m时最大主应力时程曲线Fig.7　Time curve of maximum principal stress at p=20 MPa，pmax=10 MPa and p=12 m

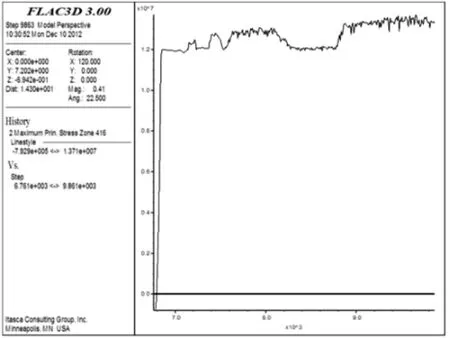
图8　p=20 MPa、pmax=30 MPa、z=0时最大主应力时程曲线Fig.8　Time curve of maximum principal stress atp=20 MPa，pmax=30 MPa and z=0 m

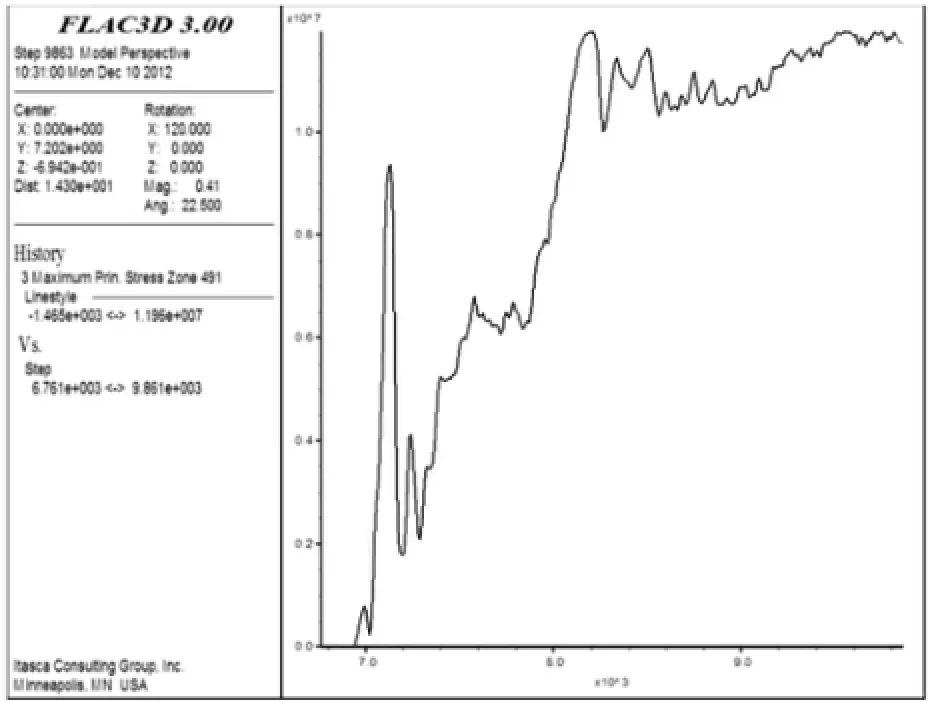
图9　p=20 MPa、pmax=30 MPa、z=6 m时最大主应力时程曲线Fig.9　Time curve of maximum principal stress atp=20 MPa，pmax=30 MPa and z=6 m

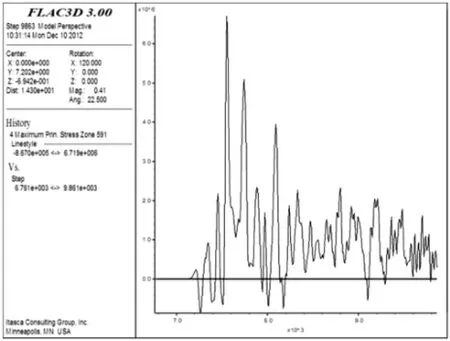
图10　p=20 MPa、pmax=30 MPa、z=12 m时最大主应力时程曲线Fig.10　Time curve of the maximum principal stress at p=20 MPa，pmax=30 MPa and z=12 m

图11　p=40 MPa、pmax=10 MPa、z=0 m时最大主应力时程曲线Fig.11　Time curve of maximum principal stress at p=40 MPa，pmax=10 MPa and z=0 m

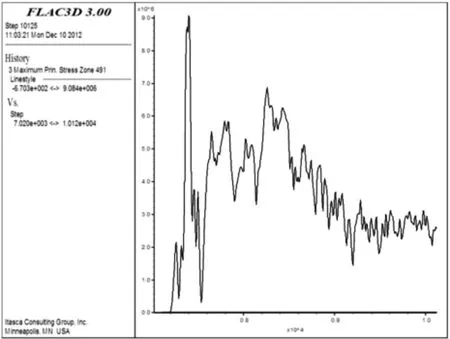
图12　p=40 MPa、pmax=10 MPa、z=6 m时最大主应力时程曲线Fig.12　Time curve of maximum principal stress atp=40 MPa，pmax=10 MPa and z=6 m

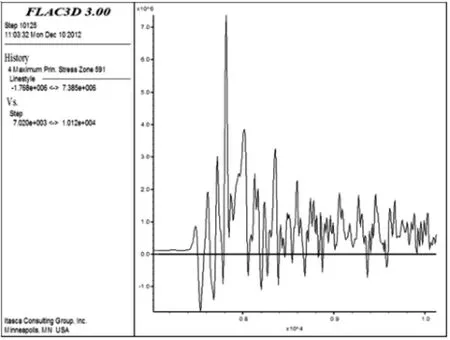
图13　p=40 MPa、pmax=10 MPa、z=12 m时最大主应力时程曲线Fig.13　Time curve of maximum principal stress at p=40 MPa，pmax=10 MPa and z=12 m

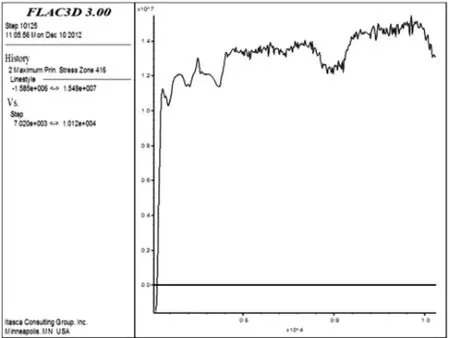
图14　p=40 MPa、pmax=30 MPa、z=0 m时最大主应力时程曲线Fig.14　Time curve of maximum principal stress atp=40 MPa，pmax=30 MPa and z=0 m

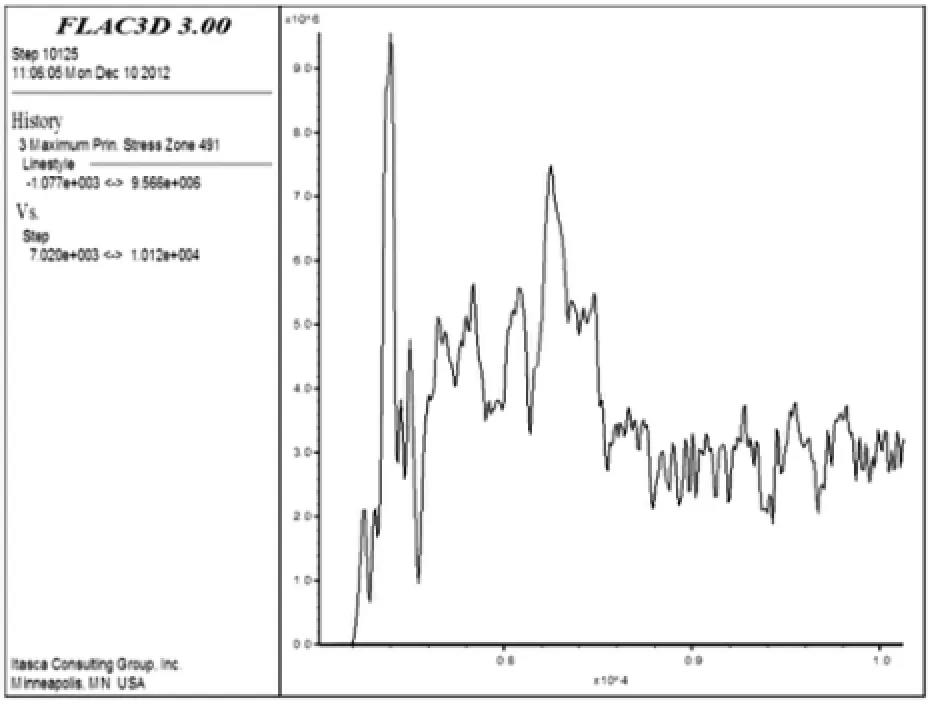
图15　p=40 MPa、pmax=30 MPa、z=6 m时最大主应力时程曲线Fig.15　Time curve of maximum principal stress atp=40 MPa，pmax=30 MPa and z=6 m

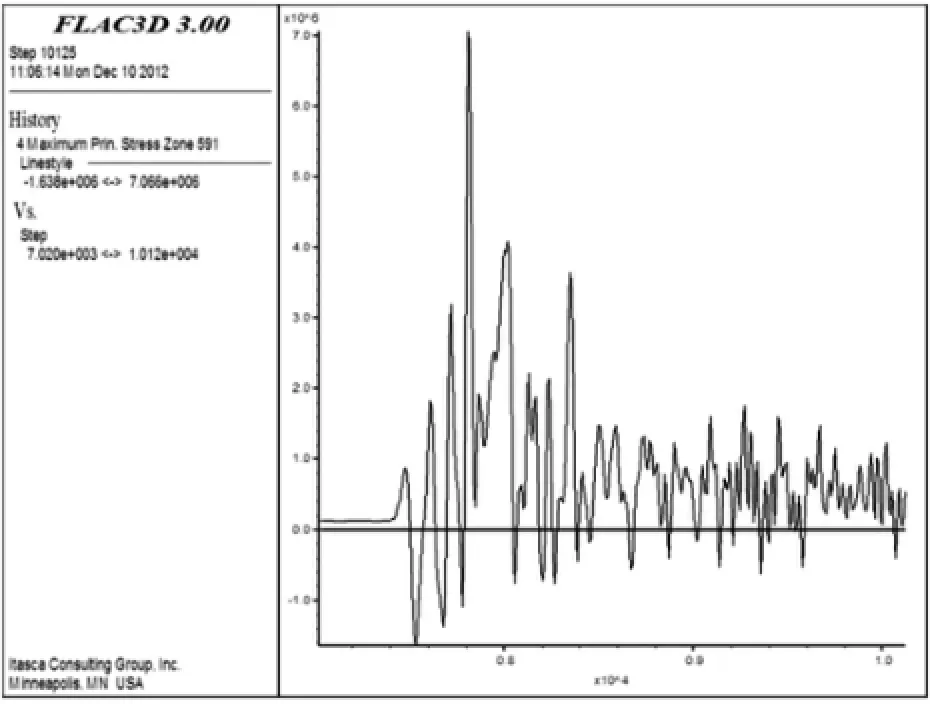
图16　p=40 MPa、pmax=30 MPa、z=12 m时最大主应力时程曲线Fig.16　Time curve of maximum principal stress at p=40 MPa，pmax=30 MPa and z=12 m

单元最大主应力时程曲线在负载p=40 MPa、应力波峰值pmax=10 MPa时如图11、图12和图13所示；单元最大主应力的时程曲线在负载p=40 MPa、应力波峰值pmax=30 MPa时如图14、图15和图16所示.根据模型上中下部单元的应力特征，上、中、下部单元的应力在应力波作用后有较大变化；随着应力波峰值的增大，矿柱模型单元的最大主应力变化不明显.

4　结　语

以大冶铁矿采空区内矿柱作为研究对象，对数值分析方案进行了设计，对采空区矿柱在动力扰动下的响应动力特征选用动力有限元法进行了综合分析.

通过对回采矿柱的动力模拟分析，可以得出如下结论：

1）当矿柱负载p=20 MPa时，矿柱模型单元的应力变化总体较稳定，模型单元应力值在应力波作用前后基本保持不变，说明负载20 MPa的该矿柱在选取的动力扰动下稳定性较差.

2）在负载p=40 MPa时，在应力波作用过程中及作用之后，矿柱模型单元应力变化的波动现象十分明显，而且随着应力波峰值的增大，单元应力波动幅度也有所增大.

3）以上2种荷载情况表明，随着矿柱荷载的增大，动力扰动对矿柱模型的影响越来越明显，模型也表现出越来越不稳定.表明矿柱随着所受应力的增大，也越易引起失稳而破坏.由此，当为矿柱的回采进行充填设计时，要考虑到矿柱的负载作用，矿柱的负载越小，整个采场的稳定性越好.

［1］申超霞，宋园园，王如坤，等.大冶铁矿采空区稳定性模拟分析［J］.金属矿山，2014（6）：46-49. SHEN C X，SONG Y Y，WANG R K，et al.Simulation analysis of mined-out area stability in Daye iron mine ［J］.Metal mine，2014（6）：46-49.

［2］ 廖秋林，曾钱邦.基于ANSYS平台复杂地质体FLAC3D模型的自动生成［J］.岩石力学与工程学报，2005，24 （6）：1010-1013. LIAO Q L，ZENG Q B.Automatic model generation of complex geologic body with FLAC3Dbased on ANSYS platfoum［J］.Chinese journal of rock mechanics and engineering，2005，24（6）：1010-1013.

［3］谢和平，陈忠辉，周宏伟，等.基于工程体和地质体相互作用的两体力学模型初探［J］.岩石力学与工程学报，2005，24（9）：1457-1464. XIE H P，CHEN Z H，ZHOU H W，et al.Study of two-bodymechanicalmodelbasedoninteraction between structural body and geo-body［J］.Chinese journal of rock mechanics and engineering，2005，24 （9）：1457-1464.

［4］ 任高峰，张世雄，彭涛.大冶铁矿矿东露天转地下开采数值模拟研究［J］.化工矿物与加工，2006（2）：20-23. REN G F，ZANG S X，PENG T.The numerical simulation discussion on surface mining to underground mining in the east pit of Daye iron mine［J］.Industrial minerals&processing，2006（2）：20-23.

［5］刘洪强，张钦礼，潘常甲，等.空场法矿柱破坏规律及稳定性分析［J］.采矿与安全工程学报，2011（1）：138-143. LIU H Q，ZHANG Q L，PAN C J，et al.Analysis of the failure law and stability of the pillar in open stope mining ［J］.Journal of mining&safety engineering，2011（1）：138-143.

［6］刘晓明，罗周全，杨承祥，等.基于实测的采空区稳定性数值模拟分析［J］.岩土力学，2007，28（10）：521-526. LIU X M，LUO Z Q，YANG C X，et al.Analysis of stability of cavity based on cavity monitoring［J］.Rock and soil mechanics，2007，28（10）：521-526.

［7］王纯祥，白世伟.三维地层信息系统与有限元方法集成研究［J］.岩石力学与工程学报，2004，23（21）：3695-3699. WANG C X，BAI S W.Study on integration of 3D strata information system and FEM［J］.Chinese journal of rock mechanics and engineering，2004，23（21）：3695-3699.

［8］ 王涛，陈晓玲，杨建.基于3DGIS和3DEC的地下洞室围岩稳定性研究［J］.岩石力学与工程学报，2005，24 （19）：3476-3481. WANG T，CHEN X L，YANG J.Study on stability of underground cavern based on 3DGIS and 3DEC［J］. Chinese journal of rock mechanics and engineering，2005，24（19）：3476-3481.

［9］朱维申，李晓静，郭彦双，等.地下大型洞室群稳定性的系统性研究［J］.岩石力学与工程学报，2004，23 （10）：1689-1693. ZHU W S，LI X J，GUO Y S，et al.Systematic study of stability of large underground houses［J］.Chinese journal of rock mechanics and engineering，2004，23（10）：1689-1693.

［10］郭家能.基于某铁矿采空区稳定性数值模拟分析［J］.现代矿业，2012（9）：24-26. GUO J N.Numerical simulation analysis on the stability of an iron ore goaf［J］.Morden mining，2012（9）：24-26.

［11］张海波，宋卫东.基于FLAC 3D数值模拟的采空区稳定性分析［J］.黄金，2013，34（3）：31-34. ZHANG H B，SONG W D.Analysis on the stability of mined cavity based on FLAC 3D numerical simulation ［J］.Gold，2013，34（3）：31-34.

［12］朱良峰，吴信才，刘修国.基于钻孔数据的三维地层模型的构建［J］.地理与地理信息科学，2004，20（3）：26-30. ZHU L F，WU X C，LIU X G.3D stratum modeling based on borehole data［J］.Geology and geo-information science，2004，20（3）：26-30.

［13］LEMON A M，JONES N L.Building solid models from boreholes and user-defined cross-sections［J］.Computers&geosciences，2003，29（5）：547-555.

［14］ 过江，古德生，罗周全.金属矿山采空区3-D激光探测新技术［J］.矿冶工程，2006，26（5）：16-19. GUO J，GU D S，LUO Z Q.A new technique of 3-D laser survey of finished stopes in metal mines［J］. Mining and metallurgical engineering，2006，26（5）：16-19.

［15］孙国权，李娟，胡杏保.基于FLAC3D程序的采空区稳定性分析［J］.金属矿山，2007（2）：29-32. SUN G Q，LI J，HU X B.FLAC3D-based stability analysis of mined-out area［J］.Metal mine，2007（2）：29-32.

本文编辑：龚晓宁

Stress Analysis on Pillar Recovery Process of Daye Iron Mine Based on FlAC3D

ZHOU Dehong，LI Wen，FENG Hao，WANG Haoran
School of Resource and Civil Engineering，Wuhan Institute of Technology，Wuhan 430074，China

To increase resource recovery，the residual pillars are needed for secondary recovery at the late stage in the metal and non-metal mines.However，the damage of the pillar structure can lead to the changes of the stope mechanic status，and even affects the stability of the whole mined-out area.Taken Daye iron mine as a case，the response characteristics and distribution discipline of the goaf were analyzed under the dynamic disturbance by using the dynamic finite element analysis.The stress changes with time of the vertically circular pillar with the diameter of 3 m，height of 12 m were simulated using FLAC3D.Results show that，at the pillar loads of 20 MPa，40 MPa，the affect of the dynamic disturbance is more obvious on the pillars with the load increasing，easily causing instability of the pillars.The stability and safety are better in the entire stope when the pillar load is smaller.Thus，we should take full account of the pillar load during the refilling design.

pillar；stress；fast lagrangian analysis of continua；goaf

TD853，TD325

A

10.3969/j.issn.1674-2869.2016.03.015

1674-2869（2016）03-0277-06

1引言

2016-04-22

2015年安全生产重大事故防治关键技术科技项目（hubei-0008-2015AQ）；湖北省安全生产监督管理局2015年、2016年安全生产专项资金项目；湖北省教育厅2014年度高校青年教师深入企业行动计划项目（XD2014132）；武汉工程大学2014年研究生教育教学改革研究项目（yjg201407）

周德红，博士，副教授.E-mail：zhoudehongwuhan@163.com坍塌.了解矿山采空区群的整体稳定性，研究承受高应力下矿柱对动力扰动的响应有非常重要的实践指导意义［1-3］.基于上述考虑，在对现场详尽调查的基础上，笔者选用动力有限元法研究湖北大冶铁矿采空区动力扰动下的响应动力特征，通过使用FLAC3D（Fast Lagrangian Analysis of Continua）软件计算，综合分析采空区矿柱负载在20 MPa、40 MPa的情况下的应力分布规律，为矿柱安全回采、充填设计提供理论依据.

为了增加资源回收率，金属非金属矿山在回采后期需要对残留矿柱进行二次回采.矿柱结构破坏必然引发采场力学状态发生变化，甚至影响整个采空区的稳定性.矿柱的回收对于采空区处理、资源节约等方面具有重要的经济和安全意义，正确合理确定矿柱回采方式是矿柱回收过程中必须解决的关键问题.大量工程实践案例表明，矿山采空区任一矿柱的失稳易形成多米诺连锁效应的