离心泵转速对工作点参数的影响

齐　济，河星武

(大连民族大学 生命科学学院，辽宁 大连 116605)



离心泵转速对工作点参数的影响

齐济，河星武

(大连民族大学 生命科学学院，辽宁 大连 116605)

利用离心泵特性曲线测定装置，在固定阀门开度下，通过改变离心泵的转速，测出不同阀门开度下系统管路的特性曲线；在固定转速下，通过改变系统管路阀门开度，测出不同转速下离心泵的特性曲线。绘制出所有特性曲线，找出泵的工作点。拟合出所有特性曲线的方程，统计分析出转速对泵工作点的流量、扬程和轴功率的影响。结果表明：当转速变化量为20 %时，流量与转速[qv1/qv2=k1(n1/n2)]的比例系数k1=0.96～1.52；扬程与转速[H1/H2=k2(n1/n2)2]的关系式中k2=0.81～1.56；轴功率与转速(N1/N2=k3(n1/n2)3)的关系式中k3=0.66～1.37。根据离心泵的比例定律，理论上k1≈k2≈k3≈1，但实验证明，离心泵的比例定律系数在实际工作中变化范围较大,应予修正。讨论了实验条件下离心泵的适配管路，为离心泵在实际应用中节约能源和高效利用提供依据。

离心泵；转速；特性曲线；泵工作点；效率

离心泵是液体输送通用机械,广泛应用于国民经济的各个部门，包括工厂、矿山、实验室等。因为输送液体是靠离心泵和管路系统相互配合完成的，所以当离心泵安装在一定管路中工作时，离心泵所提供的扬程及流量必然与管路要求供给的扬程及流量相一致。若将泵特性曲线(H-qv)与管路特性曲线(He-qv)绘在一张图上，则两条曲线的交点即为离心泵的工作点。泵的特性曲线由泵的结构和转速决定，当泵结构一定的条件下，它只受转速的影响[1]。目前，有关离心泵的研究包括：泵开始和结束时的特性曲线[2]，粘度对泵特性曲线的影响[3]，数学模型预测离心泵的特性曲线[4]，多级和单泵的比较[5]，特性曲线的绘制[6-7],离心泵最佳工作点的确定等[8]，尚未有转速对离心泵工作点影响的研究。

本文在实验的基础上，研究转速对泵工作点的流量、扬程和轴功率的影响，讨论泵高效利用时管路的条件，这项工作将对离心泵的有效利用提供参考。

1　实验装置与方法

利用化工原理实验室的离心泵性能测定装置进行实验。实验过程中，在固定阀门开度的条件下，通过调整转速测定管路特性曲线；在固定离心泵转速的条件下，通过调整阀门开度测定离心泵的特性曲线。

1.1实验装置

实验装置如图1，由天津大学化工学院化工基础实验中心组装。装置中输水设备为不锈钢离心泵，型号为WB70/055，其他参数：真空表测压位置管内径d1=0.025 m, 压强表测压位置管内径d2=0.025 m, 真空表与压强表测压口之间的垂直距离h0=0.18 m, 实验管路内径d=0.040 m, 电机效率为60 %。流量测量采用涡轮流量计，其仪表常数为79.469次·升-1。

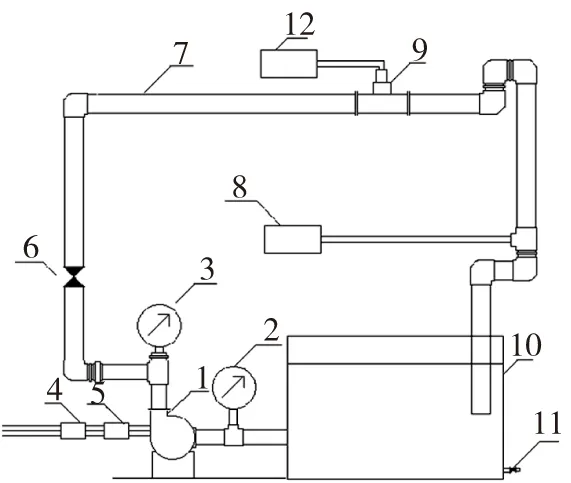
1.离心泵(WB70/055)；2.真空表；3.压力表；4.变频器；5.功率表；6.流量调节阀；7.实验管路； 8.温度计；9.涡轮流量计；10.实验水箱；11.放水阀；12.频率计

图1离心泵性能测定实验装置流程示意图

1.2实验方法

(1)改变阀门的开度。实验装置中所配备离心泵的转速可调，最大转速为3 000 r·min-1,每改变120转测定一组数据。例如，在3 000 r·min-1条件下，改变管路上的阀门开度，从阀门完全打开开始至完全关闭，每次改变开度，使流量间隔0.453 m3·h-1，在每一个开度下，当流体达到稳定输送时，测定泵前真空度、泵后表压、流量、流体温度、功率表读数。以此类推，继续测2 880 r·min-1下的数据，直到测至600 r·min-1为止(600 r·min-1以下流量几乎为零，无法测定)。

(2) 改变泵的转速。实验装置中管路的阀门开度可调，最大是全开，最小是全关，以流量间隔为0.453 m3·h-1改变开度(阀门开度在离心泵转速为3 000 r·min-1的条件下调定，共设20(m=1～20)个开度。例如从最大开度做起(m=1)，即阀门完全打开，改变转速(n=600～3 000 r·min-1)20次，使转速间隔120 r·min-1，在每一个转速下，当流体达到稳定输送时，测定泵前真空度、泵后表压、流量、流体温度、功率表读数。以此类推，在3 000 r·min-1转速下，将阀门从全开状态关小，使流量减少0.453 m3·h-1，此时阀门开度设为m=2，测定开度2下的数据，直至流量小于0.453 m3·h-1(m=20)时为止。

2　结果与讨论

实验测得809组有效数据，根据流体动力学柏努利方程式，分别计算出扬程，然后绘出离心泵特性曲线和管路特性曲线，用多项式拟合法拟合出每条曲线的方程，计算出泵特性曲线(H-qv)与管路特性曲线(He-qv)的交点，即工作点，从而确定工作点的流量、扬程、轴功率和效率。进而定量分析转速变化对工作点的扬程(H)、流量(qv)和轴功率(N)的影响，讨论泵工作点的高效区。

2.1数据处理

固定型号的离心泵，在一定转速下，离心泵的流量随管路阀门开度改变而改变，离心泵的扬程(H)、轴功率(N)及效率(η)均随流量(qv)改变而改变。通常通过实验测出H-qv、N-qv及η-qv关系，绘制特性曲线。特性曲线是确定泵的适宜操作条件和选用泵的重要依据。在一定的管路条件(阀门开度不变)下，离心泵的流量随转速的改变而改变，实验测出的He-qv之间的曲线为管路特性曲线。

(1)H的测定。在泵的吸入口和压出口之间列柏努利方程(1)；整理得方程(2)，为扬程计算公式；(3)为离心泵效率计算公式。

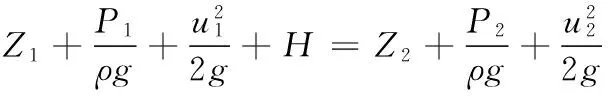
(1)

(2)

(3)

式中：Z2-Z1=h0=0.18 m；P1通过泵入口真空表测得(转换成绝压Pa)；P2通过泵出口压力表测得(转换成绝压Pa)；u1,u2通过所测定的流量qv除以管路的横截面积计算得出(m·s-1)；将这些值代入上式即可求得H的值(m)。管路特性方程中的He以同样的方法求出(m)。η为泵效率(%)；ρ为流体密度(kg·m-3) (流体为水，实验平均温度25 ℃，密度取997 kg·m-3)；g为重力加速度9.81 m·s-2；H为扬程(m)；N为轴功率(W)。

(2)N的测定。功率表测得的功率为电动机的输入功率。由于泵由电机直接带动，传动效率可视为1.0，所以泵的轴功率N=电机的输出功率, 而电机的输出功率=电机的输入功率×电机的效率，功率表的读数为电机的输入功率，所以泵的轴功率N=功率表的读数×电机效率。

2.2特性曲线

数据处理后，绘出离心泵的轴功率与流量N-qv曲线，如图2；绘出离心泵的效率流量η-qv曲线，如图3(其中包含管路开度m=7时，泵工作点的效率标注)；将离心泵特性曲线H-qv和管路特性曲线He-qv绘在同一张图上，如图4。

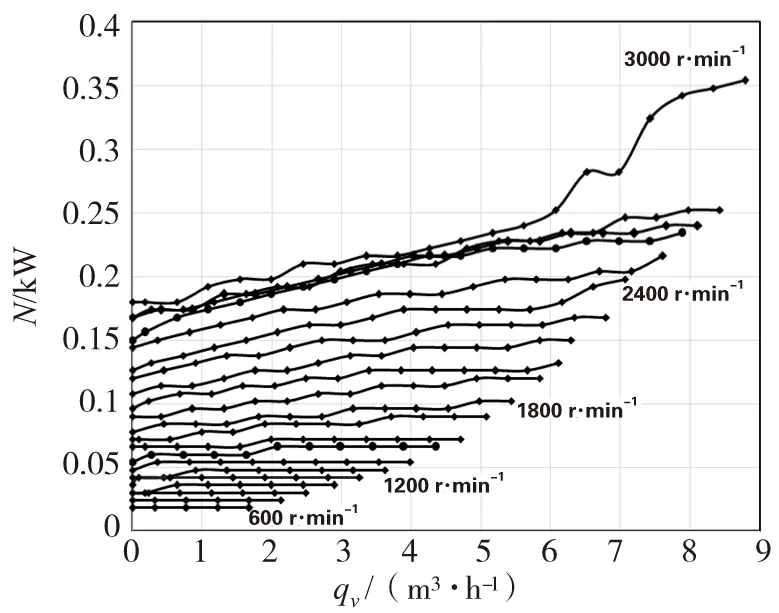
图2　离心泵轴功率与流量关系曲线

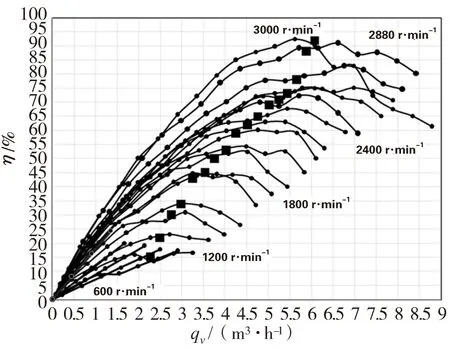
图3　离心泵效率与流量关系曲线

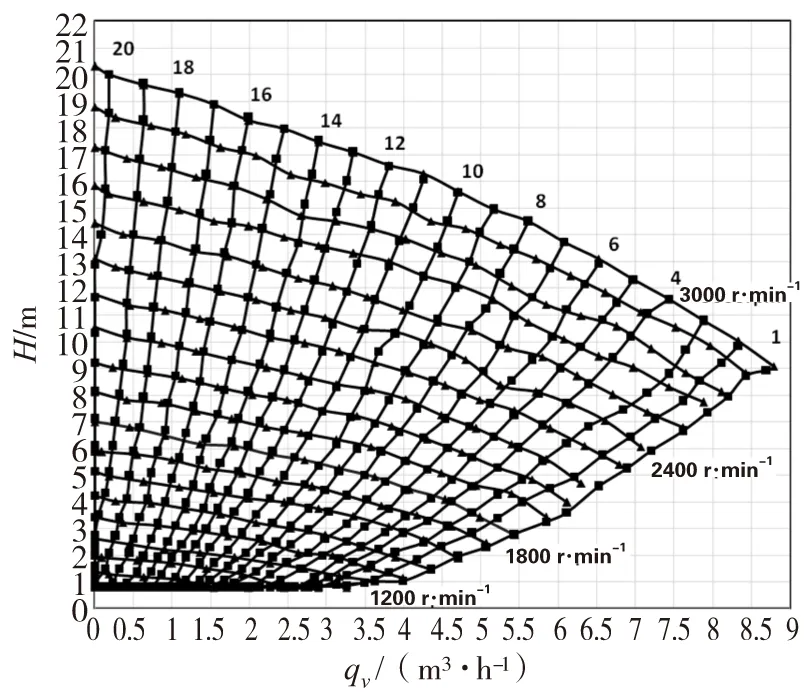
图4　离心泵特性曲线(H-qv，n=600～3 000 r·min-1)和管路特性曲线(He-qv，开度m=1～20个)

2.3拟合方程

采用多项式拟合的方法，当转速为3 000 r·min-1时，拟合η-qv、N-qv、H-qv之间的关系式如式(4)-(6)。管路开度m=1时He-qv之间的关系式如式(7)。

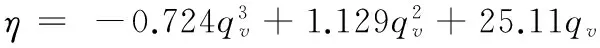
(4)

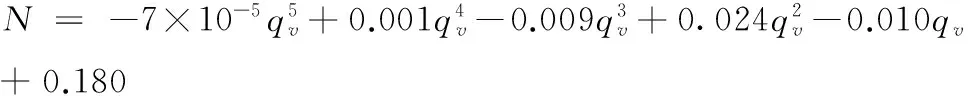
(5)

(6)

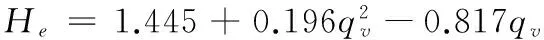
(7)

上述拟合相关系数的平方R2=0.993～0.999,表明拟合度很高，可以代替实测结果在离心泵实际应用中使用。其他转速和其他管路开度下，采用同样方法拟合，均可以达到高度拟合的结果，由于方程太多，这里省略。

2.4离心泵工作点

结合图4和H-qv及He-qv之间的拟合方程，求出泵在不同开度和不同转速下的工作点，确定工作点下的流量和扬程；结合图2和N-qv之间的拟合方程，求出工作点下泵的轴功率；结合图3和η-qv之间的拟合方程，求出工作点下的效率。统计分析工作点的转速、流量、轴功率之间的关系，发现在转速变化20 %的范围内，各参数符合方程(8)-(10)。

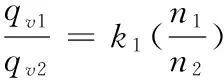
(8)

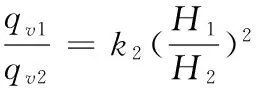
(9)

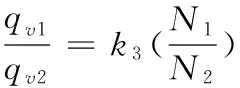
(10)

式中：k1=0.96～1.52；k2=0.81～1.56；k3=0.66～1.37。理论上k1=k2=k3，实际应用中，在转速变化小于20 %的条件下，一般取k1≈k2≈k3≈1。通过上述实验结果，在相应20 %转速变化范围内统计分析得出，比例系数变化较大，实际应用中需要进行修正。本实验转速在1 320～3 000 r·min-1范围内变化时，当变化量小于20 %，则k1=0.96～1.25；k2=0.94～1.33；k3=0.66～1.26，系数范围变小，因此应用比例定律时，应该在离心泵所使用的转速范围内进行修正。对于管路特性，在转速1 080～3 000 r·min-1，流量在2.27～6.07 m3·h-1范围内，管路处于阀门开度为7时，不同转速下，离心泵的工作点效率均处在较高点(在图3中已标出)。说明使用离心泵时，在主要的流量范围内，需要有一个适配的管路系统，若管路不合适，如实验中管路处于其他开度条件下(临近开度6和8属类似管路除外)，离心泵工作效率均会明显降低，造成能源浪费。

3　结　语

工程应用中，已有管路系统选择离心泵时，需要选择合适的型号，通常是以能够完成流体输送任务(流量和扬程要求)为主要选型标准；其次考虑实际可以达到的安装高度，防止汽蚀现象的产生；第三考虑工作点效率大于该转速下最高效率的92 %为好。本文研究结果表明：转速对离心泵工作点参数的影响与理论上的比例定律有偏差，具体应用时需要修正；对于已有的泵设备，它会有一个最适配的管路系统，将已有的泵应用于最合适的管路系统中，在主要流量范围内和主要的可控转速下，工作效率均处在最高点，这样就可以有效地利用能源，节约流体输送成本。

[1] 杨祖荣, 刘丽英, 刘伟. 化工原理[M]. 北京：化学工业出版社, 2015.

[2] CHALGHOUM I, ELAOUD S, AKROUT M, et al. Transient behavior of a centrifugal pump during starting period[J]. Applied Acoustics , 2016 (109): 82-89.

[3] LI W G. Effects of viscosity on turbine mode performance and flow of a low specific speed centrifugal pump[J]. Applied Mathematical Modelling, 2016 (40): 904-926.

[4] BARBARELLI S, AMELIO M, FLORIO G. Predictive model estimating the performances of centrifugal pumpsused as turbines[J]. Energy,2016 (107): 103-121.

[5] RAKIBUZZAMAN，SUH S H, KYUNG-WUK K, et al. A study on multistage centrifugal pump performance characteristics for variable speed drive system[J]. Procedia Engineering, 2015(105):270-275.

[6] 陈国奋, 陈秀宇，余美琼. Origin在化工原理离心泵特性曲线测定中的应用[J]. 福建师大福清分校学报, 2012(113): 62-68.

[7] 吴小平, 把多铎, 胡沙沙，等. 基于MATLAB离心泵特性曲线的拟合与绘制[J]. 中国农村水利水电, 2010(51): 144-146.

[8] 杨文国. 离心泵特性曲线和管路特性曲线确定最佳工作点的方法在何家岩金矿排水系统中的应用[J]. 有色矿冶，2013(29): 52-55.

(责任编辑邹永红)

Influence of Rotating Speed of Centrifugal Pump on Its Parameters at Operating Point

QI Ji, HE Xing-wu

(School of Life Science, Dalian Minzu University, Dalian Liaoning 116605, China)

Test device of centrifugal pump performance was appied to this work for determining the following data. With fixed valve opening, tube performance curve was determined by variable pump rotating speed(n). With fixed pump rotating speed, pump performance curve was determined by variable valve opening. All the above performance curves were drawn, and the pump opertating points were found. The fitting equations of both pump and tube performance were worked out. The influence of rotating speed on volume flow(qv), head(H) and power (N) at working point of centrifugal pump were statistically analysed. The results showed that when rotating speed variation was within 20%，qv1/qv2=k1(n1/n2), wherek1was from 0.96 to 1.52;H1/H2=k2(n1/n2)2, wherek2was from 0.81 to 1.56;N1/N2=k3(n1/n2)3, wherek3was from 0.66 to 1.37. According to the law of centrifugal pump. Theoreticallyk1≈k2≈k3≈1, while practically the proportional coefficients changed in a larger range. In this work, we worked out the optimum tube system for the pump in the device for the high efficiency, and offered some basement data for saving energy and high efficient research of centrifugal pump.

centrifugal pump; rotating speed; performance curve; pump operating point; efficiency

2096-1383(2016)05-0478-04

2016-07-13

辽宁省科学技术计划项目(2012221012)。

齐济(1964-)，女，辽宁辽中人，教授，博士，主要从事功能材料科学研究。

TQ016.8

A