辽东地区长白落叶松广义线性生长模型研究

李鹏

(辽宁省林业调查规划院，辽宁 沈阳 110122)



辽东地区长白落叶松广义线性生长模型研究

李鹏

(辽宁省林业调查规划院，辽宁 沈阳 110122)

长白落叶松是辽宁省主要造林树种之一，其总体质量关系到辽宁省的生态环境建设。文章根据辽宁省森林资源连续清查数据主要调查因子，基于103块调查样地建立林分生长模型，分析林分生长规律。关于模拟林分生长模型，经典的线性模型往往未能解释数据的离散部分；然而，一些离散变量真正影响林分生长。文中将林分生长特性和林木材积的关系作为一个案例研究，通过分析属性，提出了用广义线性模型分析林分生长数据。

广义线性模型；离散变量；林分生长

林分生长模型是指用一个或一组数学方程式来描述所计测的树木因子、林分状态和立地条件等变量与林分现实生长率之间的关系。一个好的林分生长模型可以预估在各种特定立地条件下林分的发展动态。因此，林分生长模型在森林经营与管理、森林经营优化决策、森林资源档案建立和数据更新等方面具有重要的意义。本研究以辽宁省落叶松林为例，基于辽宁省森林资源一类调查103块小班调查样地，通过广义线性模型建立了林分因子与林分平均蓄积的相关关系，提供对林分生长良好的预测需要依赖于变量及其持续的变化的影响。

1　研究区概况

研究地区位于辽宁省东部三市，即抚顺市、本溪市、丹东市。地理坐标123°22′—125°46′ E，39°45′—42°28′ N，本区是长白山脉的西南延伸部分，林区地貌属低山区，东高西低，平均海拔350 m，最高1 347 m，最低62 m，坡度一般在15°～25°，30°以上较少。本区属季风气候，全年平均气温4～7 ℃，积温值2 498.4～2 877.3 ℃，1月气温最低，平均在-10～-15 ℃，7月温度最高，平均在22～23.5 ℃，年降水量750～1 150 mm，且多集中在6—8月；早霜从9月下旬开始，晚霜延至5月上旬，生长期为5—10月。本区属棕壤区，主要成土岩石为花岗岩、花岗片麻岩等；主要成土母质有残积、坡积、残坡积、黄土状母质等。

2　数据来源与研究方法

2.1数据来源

本研究所用的数据均来自于辽宁省森林资源一类调查的103块样地。

2.2研究方法

2.2.1广义线性模型广义线性模型最早是由Nelder和Wedderburn(1972)提出的，该方法已被应用于森林的特征建模，有较好的发展前景。维尔弗里德等(2003)用广义线性模型、广义相加模型和分类树分析的统计方法预测在不同尺度上植物物种的空间分布。

Dobson(2001)指出，一般情况下，广义线性模型的线性回归方法的延伸，允许的时间和空间变化合并以及纳入量化。和经典的多元回归相比，广义线性模型提供了一个限制较少的形式。它们提供的除了正常和非恒定方差函数还有因变量的误差分布。有一个广义线性模型典型的假设是，所有的结果都是从同一个分布族，例如，正常的，泊松分布，或伽马绘制。一个广义线性模型分布族中的一个多元回归模型；不同的分布回归的方法个体分布随时间地点和外部因素变化不同。使用以可能性为基础的方法，这可以判断可能的因素是否对研究现象产生真正的影响。

(1)随机成分：作为一个例子，在指数分布中，定义Y是响应独立变量，不只是正常的组件。其中E(Y)=μ和恒定方差σ2；

(2)该系统的组成部分：X可能是离散变量或连续变量。由此产生的模型可以用来预测在任何表象的反应变量；

Y=b0+b1X1+b2X2+...+bkXk

在这个公式中，b0是拦截回归系数，b1值是从数据计算的回归系数。

(3)随机变量和系统组件之间的关系：线性(多元回归)模型可能不足以描述一个特定的关系，其对因变量所预测的影响在本质上可能不是线性的。文中使用关系函数克服这个问题。在本文中，响应变量被模拟为作为一个有对数关系函数的泊松随机分布。

g(μi)=log(μi)

然而，人们可以假定响应变量二项式或多项式，但结果与假定响应变量服从泊松分布得到的结果不会有所不同。

2.2.2Akaike信息准则要选择最简约的模型，Akaike信息准则(AIC)是用作自动逐步模型的选择。由于Akaike信息准则价值较低，一般来说，模型的预测值更接近观测值(Chambers，1997)。该模型可以选择用最小的Akaike信息准则。

其中，n是样本大小，是估计误差项的标准偏差，和tr(S)表示帽子矩阵

2.2.3Spearman的秩相关Spearman秩相关规定分配一个两个变量之间的独立的自由检测。但是，它对类型的相关性不敏感。Spearman秩相关，给出了一个更好地衡量相关性的方法，也是一个更好的两面独立测试。 Spearman秩相关系数的计算公式为：

其中，R(x)和R(y)是一对变量(x和y)每个含n个观测的秩。

2.2.4似然比检验在统计中，似然比检验是用来比较两个模型的拟合，统计测试(空模型)，其他(替代模型)是一个特殊情况。检验是基于似然比，它表示数据在一个模型下数据的拟合比另一个模型拟合多的次数。这种可能的比例或对数，可用于计算ρ值，或化为一个决定是否拒绝空模型的替代模型一个临界值。

2.2.5Wald检验Wald检验是检验在一个统计模型里特别的解释变量的重要性。在泊松回归里，我们有一个二进制的结果变量以及更多的解释变量。模型中每一个的解释变量有一个相关参数。Polit(1996)和Agresti(1990)有描述，Wald检验可以测试与一组解释变量相关的参数是否都为零。如果一个特定的解释变量，或一组解释变量，经Wald检验是显著的，然后与这些变量相关的参数不为零，那么这样的变量应该包含在模型中。如果经Wald检验不显著，则可以省略这些解释变量模型。

3　结果与分析

采用SPSS统计，进行广义线性模型分析。文中生长模型以林分平均蓄积为自变量，计算了三种不同的变量组合：第一种自变量组合是坡位、平均胸径和平均年龄；第二种自变量组合是坡位和平均年龄；第三种自变量组合是坡位和平均胸径。对以上三种自变量组合进行模拟，得到的模型分别为模型1、模型2、模型3。

3.1自变量为坡位、平均胸径和平均年龄的林分蓄积模型的建立

采用SPSS统计，应用广义线性模型，得到模型一系数、标准误和沃尔德95%置信区间。通过每个模型拟合优度比较的方法进行测试，将3种自变量组合应用到模型中，第一种自变量组合方案的广义线性回归模型的拟合优度如表1。

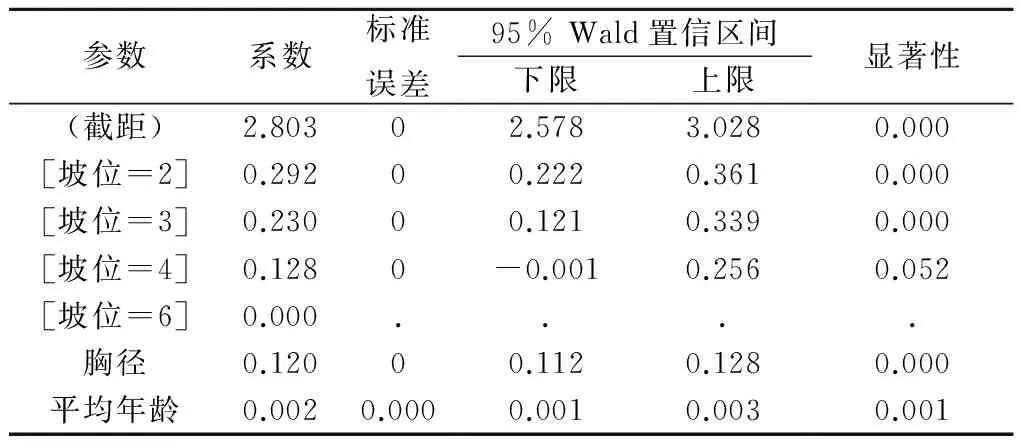
表1　模型一的拟合记录

由表1可看出，模型自变量坡位取不同的值时，系数的取值显著性均小于0.1，具有明显的差异性。

表2　模型一的拟合优度

注：自变量：坡位，平均年龄，平均胸径；因变量：平均蓄积

离差反映了估计量与真实值之间的差距，或者说可能出现结果与平均预期的偏离程度，代表风险程度的大小。赤池信息量准则(Akaike information criterion、简称AIC)是衡量统计模型拟合优良性的一种标准，该准则建立在熵的概念基础上，可以用来权衡所估计模型的复杂度和此模型拟合数据的优良性。模型一的拟合优度见表2。

3.2自变量为坡位、平均胸径的林分蓄积模型的建立

将坡位、平均胸径作为模型的自变量来建立模型，文中前面已经提及，建立的模型成为模型二，模型二系数、标准误和沃尔德95%置信区间如表3，第二种自变量组合的广义线性模型的回归模型的拟合优度见表4。

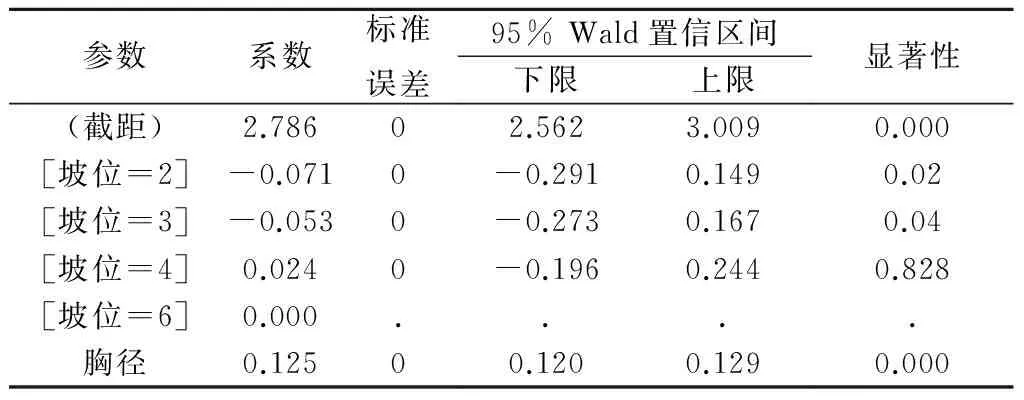
表3　模型二的拟合记录

由表3可知，当自变量坡位值取2或者3时，回归系数显著性都小于0.1，因此回归系数具有显著性；而当坡位值取4时，回归系数等于0.828，远大于0.1，因此该回归系数不具有显著性。

表4　模型二的拟合优度

注：自变量：坡位，平均胸径；因变量：平均蓄积

Akaike信息标准越低，越接近模型的现实。模型二的离差小于模型一的离差，自由度比模型一的自由度大1。对数似然值前者大于后者，相反的，Akaike信息准则 (AIC)前者大于后者，因此模型一更接近现实，即模型一拟合优度优于模型二。

3.3自变量为坡位、平均年龄的林分蓄积模型的建立

模型三是将坡位、平均年龄作为模型的自变量来建立的。表5记录了模型三系数、标准误和沃尔德95%置信区间，广义线性模型的回归模型三的拟合优度如表6。

表5　模型三的拟合记录

由表5可知，模型三的常数项以及平均年龄项的系数的显著性均小于0.1，因此系数具有显著性。当自变量坡位值取不同的值时，回归系数显著性都小于0.1，因此回归系数具有显著性，因此该模型可以较好地模拟出坡位、平均年龄与林分平均蓄积的关系。

表6　模型三的拟合优度

注：自变量：坡位，平均年龄；因变量：平均蓄积

模型三的离差大于模型一的离差，自由度比模型一的自由度大1。对数似然值大于模型一的对数似然值，Akaike信息准则 (AIC)前者大于后者，因此模型三同模型一相比，模型一更接近现实。

由此我们可得出结论，由于模型一的Akaike信息准则 (AIC)最小，其Akaike信息标准=2 817.013，而且其对数似然是最大的，对数似然值=-1 403.506，因此以坡位、平均胸径和平均年龄为自变量的模型一是这些模型之间最佳的。

3.4最优自变量组合广义线性模型Wald检验

从表7中看出，经Wald检验显著，与坡位、胸径以及平均年龄相关的这些参数都不为零，那么自变量应该包括在模型中。

表7　最优模型的Wald检验

3.5最优自变量组合广义线性模型的表达

从表7可以看出，模型中的所有系数的显著性(显著水平<0.1)。最终模型结果如下：

V=2.803+0.292*P+0.12*D+0.002*A(P=2)

V=2.803+0.23*P+0.12*D+0.002*A

(P=3)

V=2.803+0.128*P+0.12*D+0.002*A(P=4)

其中，V指林分的平均蓄积，P指林分立地的坡位，D指林分的平均胸径。A指林分的平均年龄。

由于调查数据中坡位为6的小班只有一个，因此无法对坡位为6的林分的因子和林分蓄积的相关关系进行模拟。

4　结论与讨论

4.1以辽宁省长白落叶松林为例，基于103块调查样地，通过广义线性模型建立了林分因子与林分平均蓄积的相关关系，通过每个模型拟合优度比较的方法进行测试，最终获得模拟效果最好的模型，该模型以坡位、平均胸径为自变量，最终得出了当坡位分别为上坡、中坡、下坡的林分平均蓄积线性回归方程。回归方程如下：

V=2.803+0.292*P+0.12*D+0.002*A(P=2)；

V=2.803+0.23*P+0.12*D+0.002*A

(P=3)；

V=2.803+0.128*P+0.12*D+0.002*A(P=4)；

其中，V指林分的平均蓄积，P指林分立地的坡位，D指林分的平均胸径，A指林分的平均年龄。

该模型可预测林分的生长动态变化，从而为森林经营者提供合理林分动态信息。

4.2本文中重要的一个自变量为坡位，坡位为离散因子，在进行林分调查时，是较为容易获得的数据，将坡位作为自变量引入到林分蓄积量估计模型当中来，应用广义线性模型能较好将此类离散变量作为自变量进行估计，这大大减少了野外调查的难度和工作量。

[1] Nelder J A,Wedderburn R W.Generalized linear models[J],Roy.Statist.Soc. Ser.A,135,1972：370-384

[2] Dobson A,An Introduction to Generalized Linear Models[M],(2nd ed).CRC Press,Boca Raton,Fla.2001：145-147

[3] Thuiller W,Araújo MB,Sandra L.Generalized models versus classification tree analysis: Predicting spatial distributions of plant species at different scales[J].Veg.Sci. 2003，14：669-680

[4] Chambers J M,Hastie T J. Statistical models in S [M],London,UK: Chapman&Hall,1997：23-25

[5] Polit D.Data Analysis and Statistics for Nursing Research[J],Stamford,CT:Appleton&Lange,1996：45-46

[6] Agresti A. Categorical Data Analysis. John Wiley and Sons[M].2nd ed.New York: The Wiley Series in Probability and Statistics,1990：24-26

[7] 杨志雄,袁岱菁.非线性混合效应模型和广义线性模型拟合随机效应logistic回归的应用比较[J].中国卫生统计,2011，28(3):321-323

[8] 冯静海.广义线性模型逆回归统计研究[J].大连理工大学学报，2011，51(3):464-468

[9] 陈卓恒.负二项分布的广义线性模型及其应用[J].华侨大学学报：自然科学版,2011，32(2):226-230

Generalized Linear Models ofLarixolgensisin Eastern Region of Liaoning Province

Li Peng

(Forest Inventory ard Planning Institute,Liaoning Province,Shenyang 110122,China)

Larixolgensisis one of the main tree species in Liaoning Province,and its overall quality relates to the ecological environment of Liaoning Province.Growth model of stand was established based on 103 survey plots on the basis of the main description factor database of continuous forest inventory in Liaoning Province.The law of stand growth was analyzed.As for simulating stand growth Model,the classical linear models often failed to explain the discrete component of data.However，some discrete variables really influence the stand growth.The relationship between stand growth characters and volume of stands was discussed as a case study.Data of stand growth by using generalized linear models was proposed through analyzing attribute.

generalized Linear Models；discrete variables；stand growth

1005-5215(2016)09-0038-04

2016-06-30

辽宁省农业攻关及成果产业化项目(2014207011)

李鹏(1985-)，男，硕士，工程师，主要从事林业调查规划工作.

S791.22

A

10.13601/j.issn.1005-5215.2016.09.011