一种基于权重的云服务搜索算法
2016-09-26孙寒玉顾春华杨巍巍
孙寒玉 顾春华 万 锋 杨巍巍
(华东理工大学信息科学与工程学院 上海 200237)
一种基于权重的云服务搜索算法
孙寒玉顾春华万锋杨巍巍
(华东理工大学信息科学与工程学院上海 200237)
云计算技术迅猛发展,众多云服务的功能和服务质量有所不同。针对这种情况,提出一种服务权重计算方法。算法通过分析组合服务和原子服务的关系,结合服务实例的可靠性、新鲜度和负载度,计算服务实例权重值并排行,获得最优实例提供服务。数据分析和仿真实验表明,算法有效选择当前最优服务实例,提高云平台的可用性、效率和鲁棒性。
云计算服务组合权重计算搜索
0 引 言
随着云计算技术的发展,基于云的应用开发需求越来越迫切。开发者可以根据业务流程在云中寻找服务或服务组合,完成业务逻辑需求。随着云计算技术应用日趋广泛,云服务的增长速度也在逐渐加快,不可避免出现了大量功能相同或相似的云服务和服务组合,简单的关键词查找可以在一定程度上解决服务搜索问题,但云应用开发者需要更准确更高效的搜索方法。
服务发现和服务组合算法在Web服务中得到广泛应用,Web服务搜索排行拥有大量的研究,同时存在多种服务权重计算算法。其中一部分以服务质量作为研究重点,文献[1]通过Web服务动态组合来描述服务质量、服务提供商因子和消费因子等因素,提出基于层次分析法的质量计算方法,从而得到更高质量的服务;同样根据服务质量作为发现基础,文献[2]考虑服务的服务质量和用户对属性的偏好,根据用户选择服务行为特点,将不确定主观权重加入服务权重分析;文献[3]研究了服务组合问题,提出服务干扰模型,使用该模型描述用户对组合服务的满意度,并在计算量上做了研究;文献[4]提出基于n维空间权重距离计算,根据用户对不同服务质量属性的偏好设定权重距离,根据阈值设定返回给用户的服务。另一部分使用其他方式计算服务权重,对服务进行排行。文献[5]调用服务历史数据,抽取属性计算权重,包括信息的预处理和粗糙集匹配,实现服务发现;文献[6]提出以Web服务的关联结构作为基础的权重排行计算;文献[7]通过用户的输入和输出请求以及服务质量的约束,采用服务最优组合迭代替换的方案,快速搜索满足需求的服务组合方案;文献[8]在Web服务描述语言基础上,通过倒排序索引表和二分图匹配完成服务发现,通过两个阶段发现所需要的服务;文献[9]在领域本体语义信息的基础上,提出一种可以自适应调整领域划分、分配系统资源的服务发现体系,主要在服务的可扩展性、自组织性和自适应性上进行分析。
Web服务的权重搜索算法已趋于成熟,而云服务与Web服务有所不同,云环境中服务由运行的服务实例提供,服务实例动态存在,提供服务的能力会受当前实例的可用性、新鲜度和负载程度等因素状态的影响,单纯的服务选择是不可以直接调用的,用户希望得到的不是可以直接提供最优服务的服务实例,如何在众多实例中找到能够满足需求且服务能力最优的服务,是云框架中服务搜索的重要问题之一。因此,本文研究了Web服务的服务发现和服务组合算法及PageRank[10,11]页面搜索算法,结合云环境的特点,提出在以服务组合关系计算服务权重的基础上,根据服务实例不同时刻提供此服务的能力计算实例权重值,并进行排行显示,为用户提供最佳选择。
1 服务权重计算
服务分为原子服务和组合服务,原子服务是不可以再分的服务,可以直接调用。每个原子服务绑定一组输入输出信息,组合服务是由一系列原子服务组合而成,由各个原子服务按照一定序列协同工作而完成。本文选用OWL-S的控制结构来划分原子服务和组合服务,包括:Sequence、Split、Split-Join、Any-Order、Choice、If-Then-Else、Iterate、Repeat-While and Repeat-Until[12]。
定义1组合服务U:由原子服务集合SC(U)和原子服务关系组合SRL(U)构成。
原子服务集合SC(U):组成服务U的原子服务集合。
SC(U)={si}
其中si为原子服务。
原子服务关系组合SRL(U):组成组合服务的原子服务之间关系集合。
SRL(U)={(sm,sn)|sm,sn∈SC(U)}
(sm,sn)代表关系sm→sn,原子服务sm的输出为原子服务sn的输入,服务间可按照顺序组合。
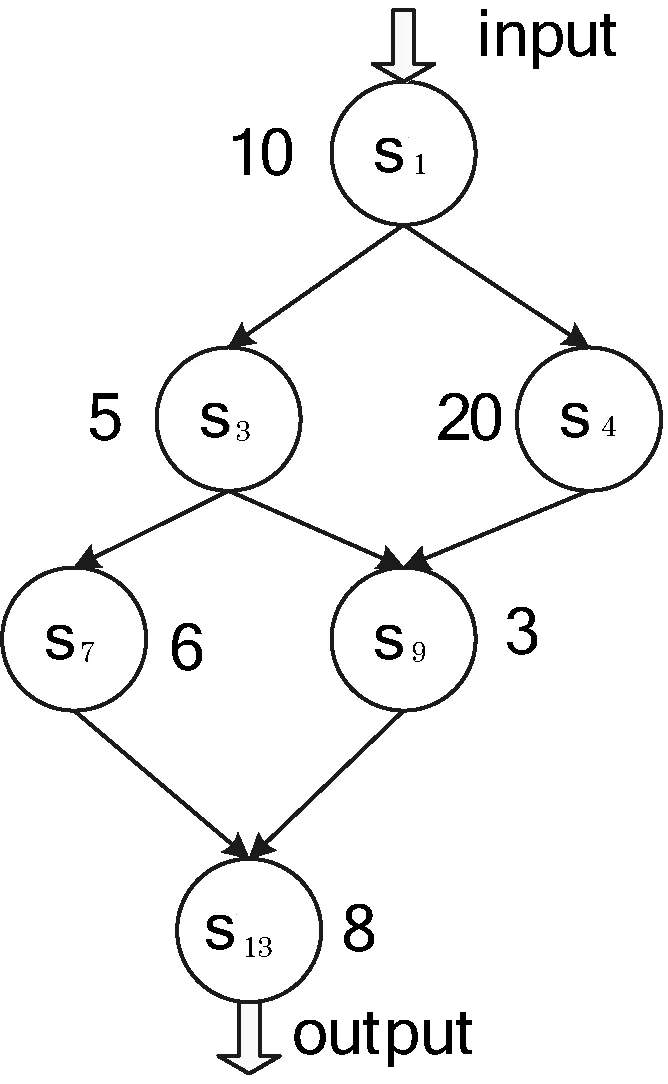
图1 组合服务A的DAG图
对于原子服务sm,sm→sn为sm的指出链接out(sm);对于原子服务sn,sm→sn为sn的指入链接in(sn)。
例如:组合服务A,由s1,s3,s4,s7,s9,s13组合而成,如图1所示。
则表示如下:
SC(A)={s1,s3,s4,s7,s9,s13}
SRL(A)={(s1,s3),(s1,s4),(s3,s7),(s3,s9),(s4,s9),(s7,s13),(s9,s13)}
定义2服务权重值SR:衡量服务质量的标准。
原子服务s的指入链接数量越多,则SR(s)越大;
指向原子服务s的服务的SR越大,则SR(s)越大。
SR(s)计算方法:
1) ∀s∈S,SR(s)=kS为所有原子服务结合,k为初始权重值;为每一个原子服务s赋予初始值。
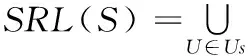
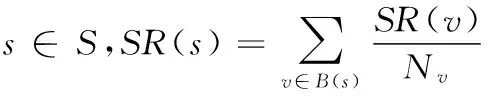
SR(s):原子服务s的权重值;
B(s):指向原子服务s的原子服务集合;

图2 原子服务权重分配图
SR(v):原子服务v的权重值,原子服务v存在链接指向原子服务s;
Nv:原子服务v所有指出链接的个数;
4) 重复计算第3步,直到任意原子服务的权重值趋向稳定。
利用上述过程计算权重值,如图2所示。
图2中原子服务关系:
SRL(S)={(…,s1),(…,s2)(s1,s3),(s2,s3),(s2,s4),
(s3,…)(s4,…)}
原子服务s1只有一条指出链接,则指出链接得到的权重为3,原子服务s2存在2条指出链接,则每条链接得到的权重为200/2=10,原子服务s3的指入链接有两条,权重值分别为3和100,所以在这一轮计算s3的权重值修改为100+3=103,s4的权重值为100。
原子服务s2的权重值远远大于s1的权重值,那么他们对原子服务s3的影响是不同的,而原子服务s1对s3的影响显的微不足道,因此在计算权限值传递时,引入阻尼系数d,取值在0~1之间,N为所有服务的个数,引入N,使所有服务的权重值相加为1。第3步计算原子服务s权重值公式为:
(1)
定义3组合服务权重值SR(U)由原子服务的权重值计算得到。由于计算复杂,且计算结果可以代表一段时间内的权重排行,因此引入计算周期Δt,经过Δt时间计算一次。计算公式为:
(2)
SR(U):组合服务U的权重值;
SC(U):组合服务U的原子服务集合;
s:组合服务U的原子服务;
SR(s):原子服务s的权重值;
N(s):原子服务s在此组合服务的原子服务关系集合SRL(U)中出现的次数;
T(U):组合服务U的原子服务关系集SRL(U)中的关联次数。
若服务权重关系及组合如图1所示,各原子服务有其各自的权重值,那么此组合服务的权重值为:
SR(A)=(10×2+5×3+20×2+6×2+3×3+2×8)/(2×7)
=8
定义4实例权重值IR(U)由实例提供服务的权重值SR(U)和服务实例运行参数计算得到。
IR(Ui)=SR(U)D(Ui)F(Ui)L(Ui)
(3)
IR(Ui):能够提供服务U的实例Ui的权重值;
SR(U):服务U的权重值;
D(Ui):实例Ui的可靠率;
F(Ui):实例Ui新鲜度;
L(Ui):实例Ui负载程度。
由各参数影响,IR的取值区间(0.002SR,2SR)。
实例运行参数包括:
1) 可靠性
实例的可靠性由实例可靠率D(Ui)衡量。
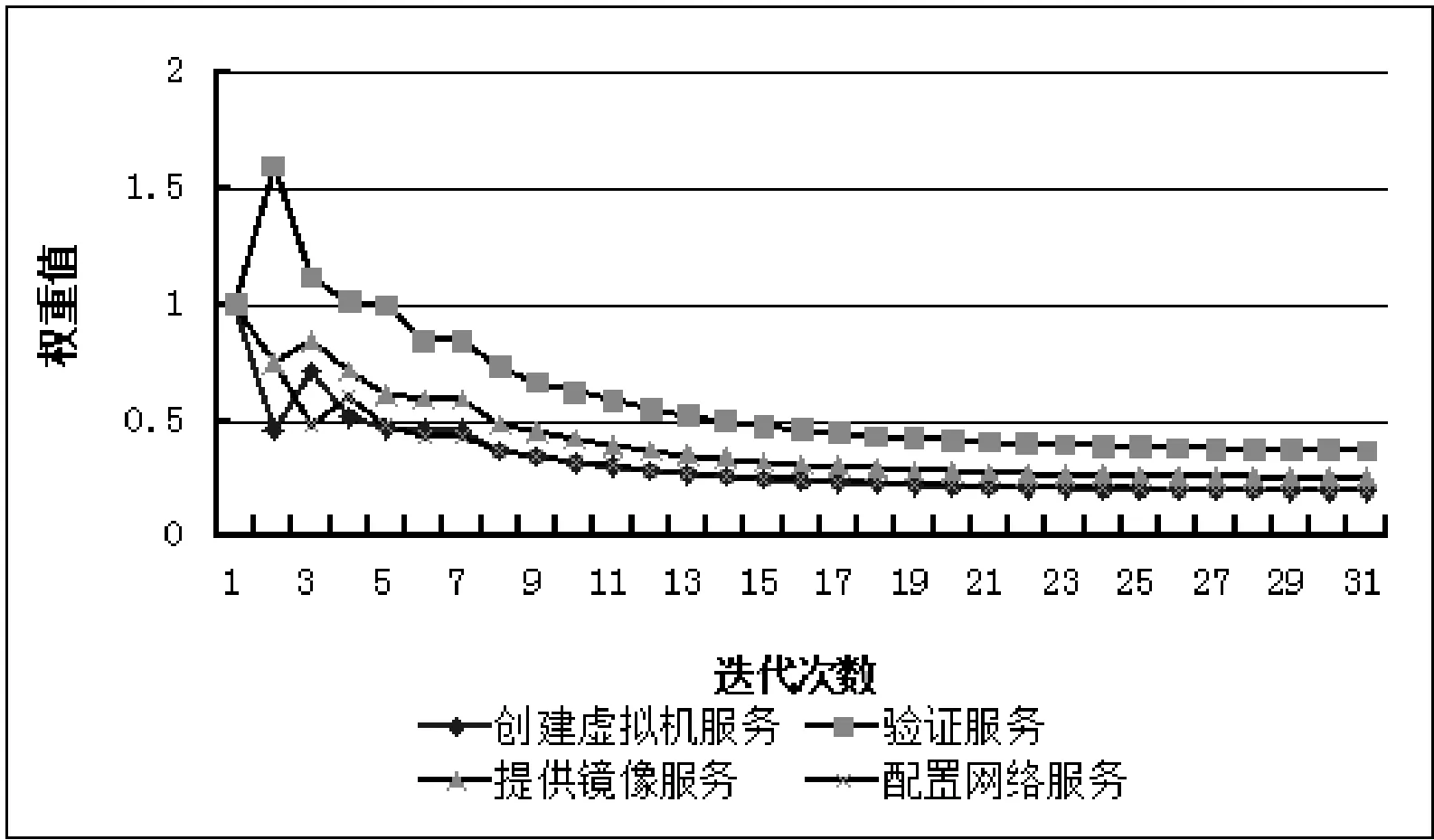
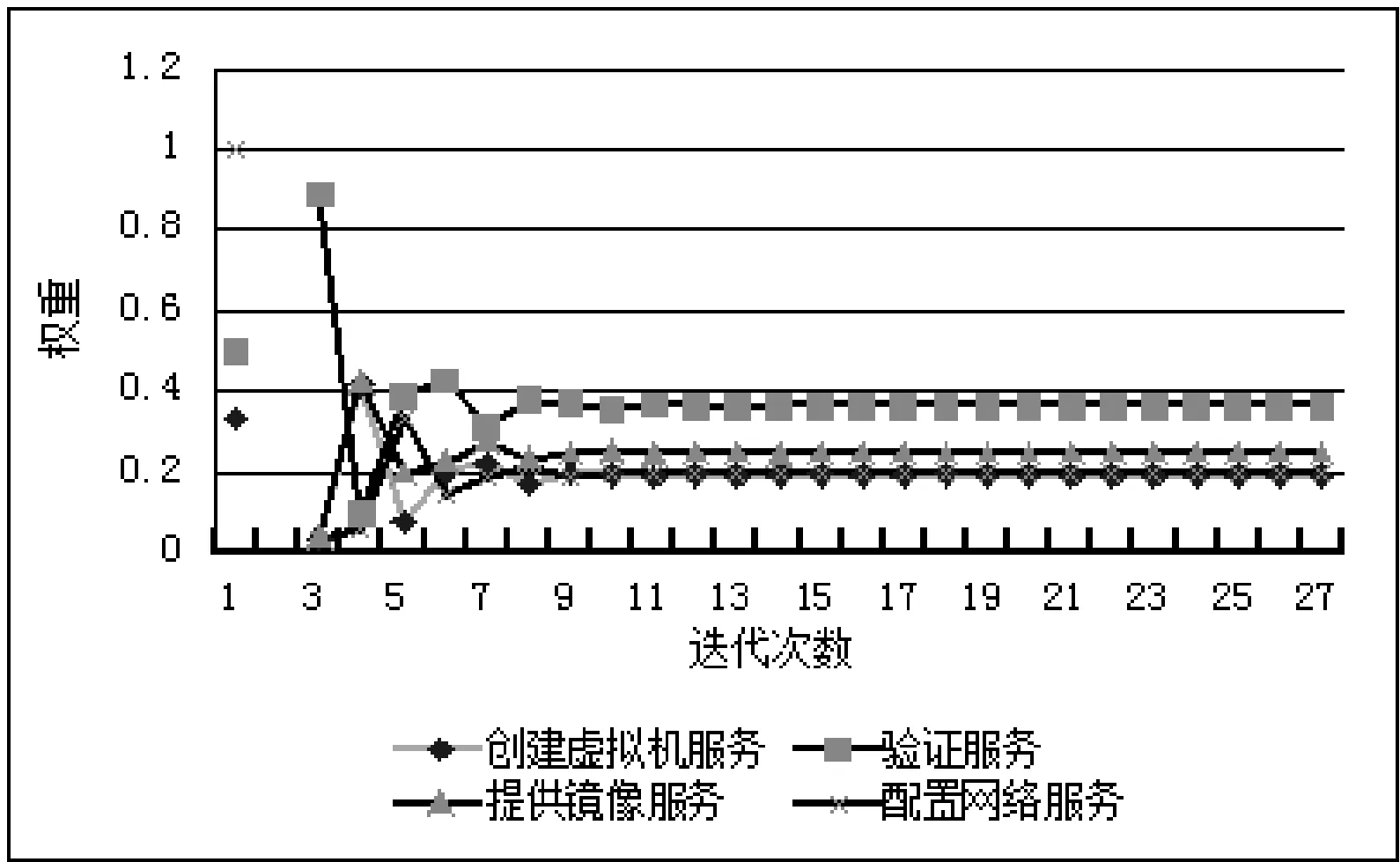
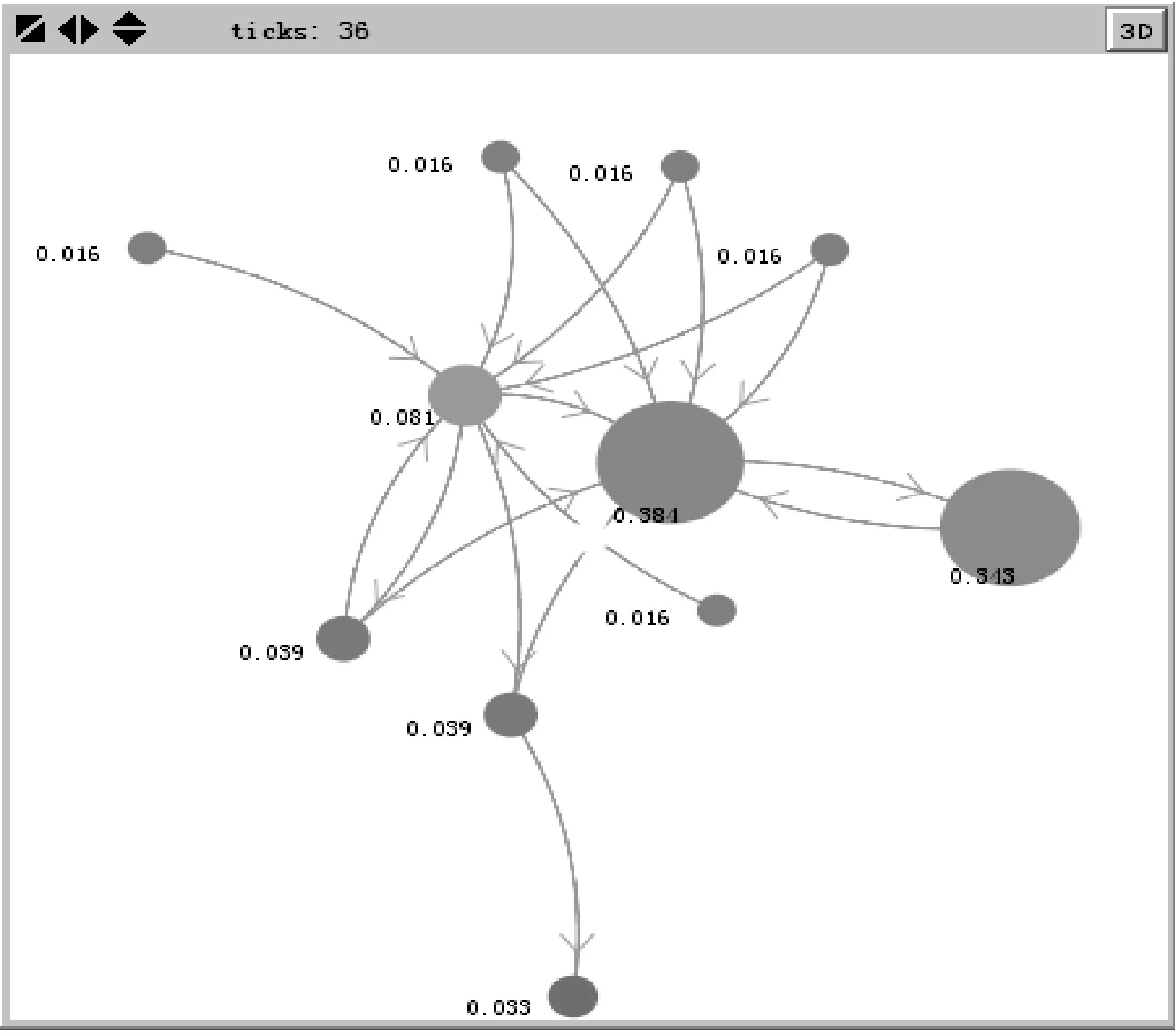
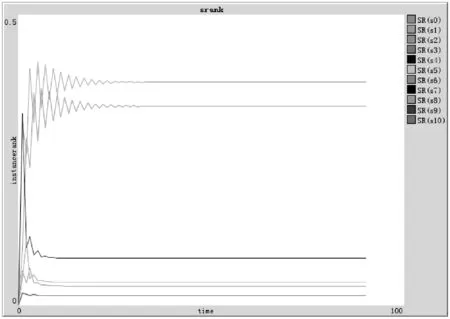
D(Ui)=1-f0 (4) f为一段给定且连续时间内测试服务发生故障的频率当实例未被使用,可靠性D(Ui)=1。 2) 新鲜度 实例的新鲜程度由实例的最后使用时间t(u)决定。 若t(u)在ɑ时间内,则F(Ui)设为1+e,其中e为比例参数公式如下: F(Ui)=1+e (5) (6) 若t(u)在大于ɑ时间,小于β时间的时间内,公式如下: (7) 若t(u)在大于β时间内,我们认为服务已经很久未被使用,服务新鲜度为恒定的值,公式如下: (8) t(now):现在的时间; t(u):实例最后使用时间。 ɑ和β为时间系数,根据云环境中服务实例的使用情况设定。当实例未被使用,F(Ui)=1。 3) 负载程度 负载程度根据服务实例动态CPU使用情况设为五个级别:无负荷(80%~100%)、轻微负荷(60%~80%)、中等负荷(40%~60%)、重度负荷(20%~40%)和完全负荷(0~20%)。 定义si为原子服务,各原子服务之间存在组合关系,通过指出链接和指入链接表示相应组合关系。如图3所示。 图3 原子服务例图及邻接表 2.1理论分析 图3中将原子服务及原子服务之间关系描述为有向图,其中s1为创建虚拟机服务,s2为验证服务,s3提供镜像服务,s4为配置网络服务有向图和矩阵式可以相互转化的,因此使用矩阵A表示原子服务及原子服务之间关系。将矩阵A中各个数值除以各行的非零要素后得到概率矩阵M,M表示原子服务si到原子服务sj的概率。 在随机过程理论中,M称为转移概率矩阵。每一次迭代过程相当于用上一次迭代结果乘以矩阵M。这种离散状态按照离散的时间随机转移过程称为马尔科夫链。设转移概率矩阵为P,若存在正整数N,使得P^N>0(每个元素大于0),这种链被称作正则链。在云存储环境的实际应用情况中,服务和服务之间的关系属于正则链。而正则链存在唯一的极限状态概率且与初始状态无关。因此,理论上可以将求解原子服务权重问题转化为求马氏链的平稳分布问题,公式如下,其中SR(si)代表原子服务si的服务权重值: SR(s1)=SR(s2)/2 SR(s2)=SR(s1)/3+SR(s3)/2+SR(s4) SR(s3)=SR(s1)/3+SR(s2)/2 SR(s4)=SR(s1)/3+SR(s3)/2 SR(s1)+SR(s2)+SR(s3)+SR(s4)=1 解得: SR(s1)=0.1875SR(s2)=0.375 SR(s3)=0.25SR(s3)=0.1875 由结果分析,指入链接越多,原子服务的权重值越高,表示该原子服务质量越好。 2.2数据分析 根据定义2计算过程计算图3中原子服务权重,不考虑阻尼系数,初始值设为1时实际迭代情况如表1和图4所示。 表1 SR(s)迭代计算表(初始权重为1) 图4 SR(s)迭代趋势图(初始权重为1) 经分析得,多次迭代后,原子服务的权重值达到平稳,与理论分析中马氏链求出结果关系如下: SR(s1):0.7499/0.1875=4.000 SR(s2):1.4999/0.375=4.000 SR(s3):0.9999/0.25=4.000 SR(s4):0.7500/0.1875=4.000 由计算结果得到,经过多次迭代的原子服务权重值与理论分析中马氏链求出结果为倍数关系。 根据式(1)计算原子服务权重,阻尼系数设为0.85,初始权重值设为1,迭代如表2和图5所示。 表2 SR(s)迭代计算表(d=0.85,初始权重为1) 图5 SR(s)迭代趋势图(d=0.85,初始权重为1) 根据式(1)计算原子服务权重值,阻尼系数设为0.85,各服务初始权重值设为指出链接的倒数,s1的初始权重值为1/3,s2的初始权重值为1/2,s3的初始权重值为1/2,s4的初始权重值为1。迭代如表3和图6所示。 表3 SR(s)迭代计算表(d=0.85,初始权重为指出链接倒数) 图6 SR(s)迭代趋势图(d=0.85,初始权重为指出链接倒数) 经分析得到,无论原子服务的初始权重值为多少,经过多次迭代,最终稳定权重值是相同的。所以,加入阻尼系数后,初始权重值对最终原子服务的权重值是没有影响的,服务权重值会最终达到平稳,且代表服务的重要性,权重值越大,则服务越重要。 在表3中,权重值在迭代了20次左右时已经达到相对平稳,大大减少了迭代次数,因此,选择好的初始权重值可以减少计算权重值的迭代次数,提高计算效率。 使用netlogo仿真平台实验,从更多服务的角度,定义11个原子服务si,如图7所示,图形圆代表服务,图形圆边的数字代表服务权重值,同时为了更好地查看效果,原子服务的权重值越大,代表其的图形圆的面积就越大。圆之间的有向连线代表服务之间的组合关系。为每一个服务赋予初始权重值,计算过程中权重值取小数点后三位,ticks代表迭代次数。 图7 实例权重分布图 图7中表示经过36次迭代后服务权重值的变化,可以分析得到,拥有最多的指入链接的圆面积最大,代表其服务权重值也是最高的0.384,说明服务的指入链接越多,证明有越多的服务可以和其组合,说明此服务越重要。 图8中将服务权重值以曲线的形式显示,可以看到,各服务最终权重值会达到稳定,并且服务越重要,其权重值越高。最终可以输出按照权重值大小排序的原子服务和其权重值。 图8 服务权重曲线图 服务权重最高的服务代表最重要的服务,此服务由云框架中不同服务实例提供,服务实例存在动态生存周期,虚拟实例具有三个参数:fresh代表实例新鲜度,取值范围(0.1,2), reliability代表实例可靠性,取值范围(0.1,1),load代表实例负载程度,取值集合{20%,40%,60%,80%,100%}。在netlogo中仿真三种因素在不同实例的运行状态。如图9所示,定义6个提供最高权重服务的实例,图形圆代表实例,图形圆边的数字代表实例权重值,实例的权重值越大,代表其的图形圆的面积就越大。 图9 实例权重分布图 图9表示提供服务的服务实例权重值在不同时刻的权重值情况,最大的圆代表的具有最高权重值的实例,代表当前时刻此实例可以提供最优的服务,提供的服务能力最高。 如图10(左)所示,曲线代表的实例权重随时刻的不同而发生变化,表明实例权重值并不是一成不变的,随着实例的新鲜度、负载程度和可信度的变化而变化,权重值高,则实例此时能够服务的能力高。 图10(右)为多个实例的权重值随时间变化的曲线,在任意时刻都可以对这些实例的权重值比较,同时输出比较结果,权重值高的则排在前面,方便用户选择。得到权重值最高,最优提供服务的实例。 图10 实例权重曲线图 通过数据分析可以得到无论原子服务的初始权重值设为多少,经过多次迭代,最权重值会逐渐收敛,达到稳定;加入阻尼系数使得无论原子服务的初始权重值设为多少,最后得到的权重值是一致的;加入服务数量N使得最终得到的服务权重值总和为1,控制原子服务权重值的数量级;初始权重值取值会影响到权重值计算的迭代次数,初始权重值取值越接近总服务数的倒数,最终权重值达到平稳的计算次数就越少,所以初始值的选择会直接影响计算效率。 由仿真实验可以得到服务的指入链接越多,此服务的权重值就越高,则说明与此服务组合的服务越多,此服务越重要。计算得到实例权重值,实例权重值在不同时刻有明显不同,实例的服务能力在不同时刻受其新鲜程度、可靠性和负载度的影响,而算法可以对多个提供相同服务的实例进行新鲜程度、可靠性和负载度的对比,提高云平台的整体性能,增加了云平台提供服务的高可用性、减少数据迁移量,提高效率,有效提高云平台的鲁棒性。 本文针对以服务实例提供计算资源的云平台,通过服务组合关联计算服务权重值,从云平台整体性能的角度,对可靠性、数据迁移量和鲁棒性进行分析,将实例生存周期中的可靠性、新鲜度和负载度作为参数计算实例权重值,并对提供服务的虚拟机实例进行权重值排序,为云应用开发者提供当前时刻最优选择。算法提高服务权重值及实例权重值的计算效率,但与服务请求内容无关。因此在之后的研究中将使用领域本体语言描述服务及服务组合,利用本体相似算法,达到服务搜索的准确性和高效性。 [1] 张琦,侯红.Web服务动态组合中QoS计算方法研究[J].计算机工程,2011,37(12):41-43. [2] 樊志强,申菊芳,王守信.基于不确定主观权重的Web服务选择[C]//2009中国计算机大会论文集,2009:595-603. [3] 王慧,杨德国,高远.一个基于QoS的服务路径发现和恢复算法[J].东北大学学报:自然科学版,2008,29(2):209-212. [4] 李珍,王红兵.Web Services的权重空间距离和定量选择[J].计算机工程与科学,2011,33(10):182-185. [5] 赵旭,黄永忠,安留洋.基于属性权重和粗糙集的网格服务发现算法[J].计算机应用,2012,32(1):167-169. [6] 朱怡安,雷万保.基于服务关联模型的服务排序算法——ServiceRank[J].电子科技大学学报,2011,40(4):607-611. [7] 马环宇,姜伟,虎嵩林.QSynth-TopK:一个支持Top K查询的质量敏感的自动服务组合系统[J].电子学报,2012,40(10):1933-1937. [8] 李季辉,贾永伟.基于索引表和二分图的Web服务操作发现[J].计算机工程,2012,38(13):37-39,43. [9] 姚燚,曹玖新,刘波.基于语义的可扩展Web服务注册与发现机制[J].东南大学学报:自然科学版,2010,40(2):264-269. [10] Kumar G,Duhan N,Sharma A K.Page Ranking Based on Number of Visits of Links of Web Page[C]//International Conference on Computer & Communication Technology (ICCCT),2011. [11] Liu Y,Xu P.The Research of Optimizing Page Ranking Based on User’s Feature[C]//International Conference on Industrial Control and Electronics Engineering,2012. [12] OWL-S:Semantic Markup for Web Services[EB/OL].(2004-11-22).[2014-09-11].http://www.w3.org/Submission/OWL-S/,2004. A CLOUD SERVICE SEARCHING ALGORITHM BASED ON WEIGHT Sun HanyuGu ChunhuaWan FengYang Weiwei (SchoolofInformationScienceandEngineering,EastChinaUniversityofScienceandTechnology,Shanghai200237,China) Cloud computing technology is developing rapidly, various functions and qualities of cloud services differ from each other. In view of this, we propose a service weight computation algorithm. The algorithm computes and ranks the weight of service instances by analysing the relationship of atom service and composition service and combining with reliability, novelty and load degree of service instances to obtain best instance for providing service. Data analysis and simulation experiment all show that the algorithm can pick up optimal current service instance, and promote cloud platform’s high availability, efficiency and robustness. Cloud computingService compositionWeight computationSearching 2014-09-17。孙寒玉,硕士,主研领域:云计算方面研究。顾春华,教授。万锋,高级实验师。杨巍巍,硕士。 TP3 A 10.3969/j.issn.1000-386x.2016.03.008
2 数据分析


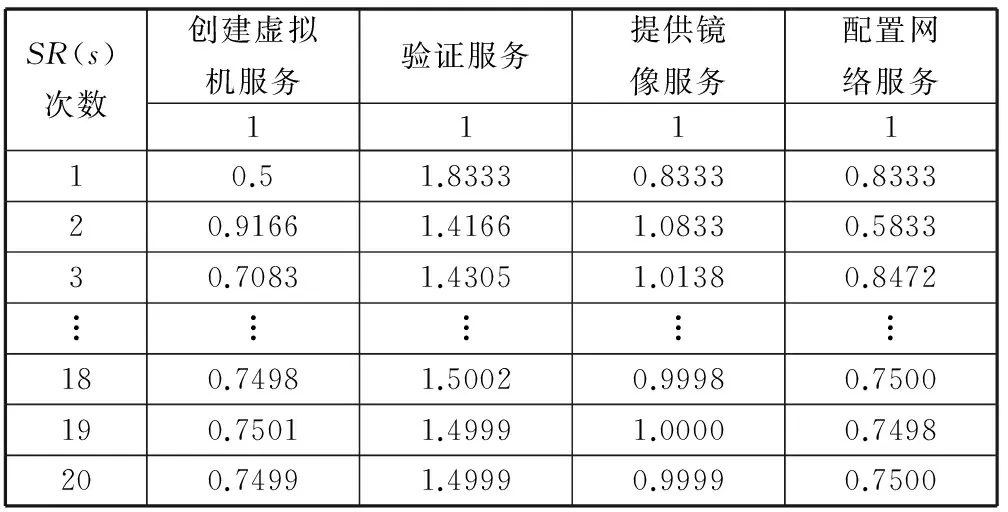



3 实验验证


4 实验结论
5 结 语
