A BINARY INFINITESIMAL FORM OF TEICHMUüLLER METRIC AND ANGLES IN AN ASYMPTOTIC TEICHMUüLLER SPACE∗

Yan WU（吴艳）

LMIB and School of Mathematics and Systems Science，Beihang University，Beijing 100191，China

School of Science，Linyi University，Shandong 276005，China E-mail∶wuyan@lyu.edu.cn

Yi QI（漆毅）

LMIB and School of Mathematical Science and Systems Science，Beihang University，Beijing 100191，China

E-mail∶yiqi@buaa.edu.cn



A BINARY INFINITESIMAL FORM OF TEICHMUüLLER METRIC AND ANGLES IN AN ASYMPTOTIC TEICHMUüLLER SPACE∗

Yan WU（吴艳）

LMIB and School of Mathematics and Systems Science，Beihang University，Beijing 100191，China

School of Science，Linyi University，Shandong 276005，China E-mail∶wuyan@lyu.edu.cn

Yi QI（漆毅）

LMIB and School of Mathematical Science and Systems Science，Beihang University，Beijing 100191，China

E-mail∶yiqi@buaa.edu.cn

The geometry of Teichmüuller metric in an asymptotic Teichmüuller space is studied in this article.First，a binary infinitesimal form of Teichmüuller metric on AT（X）is proved. Then，the notion of angles between two geodesic curves in the asymptotic Teichmüuller space AT（X）is introduced.The existence of such angles is proved and the explicit formula is obtained.As an application，a sufficient condition for non-uniqueness geodesics in AT（X）is obtained.

Angles of asymptotic Teichmüuller space；geodesic segment；Finsler structure；Boundary dilatation

2010 MR Subject Classification32G15；30C62；30F60

1　Introduction

In this article，a hyperbolic Riemann surface always means a Riemann surface whose universal covering is conformally equivalent to the unit disk D of the complex plane C.Let X be a hyperbolic Riemann surface and let Belt（X）be the Banach space of Beltrami differentialsX with L∝-norms.Denote by M（X）the open unit ball of Belt（X）.

For eachµ∈M（X），there is a quasiconformal mapping fµ：X→fµ（X）withµas its complex dilatation.Two elementsµand ν in M（X）are said to be Teichmüuller equivalent，denoted byµ～ν，if there is a conformal map ϕ：fµ（X）→fν（X）such that（fν）−1◦ϕ◦fµis homotopic to the identity mapping of X modulo the ideal boundary∂X.The Teichmüuller space of X is the space of Teichmüuller equivalence classes：where［µ］Tis the Teichmüuller equivalence class containingµ.It is known that T（X）is a complex manifold modeled on a complex Banach space such that the quotient map Φ：M（X）→T（X）is a holomorphic split submersion.

There is a natural metric dT（［µ］，［ν］）on T（X），which is called the Teichmüuller metric of T（X）.It coincides with the Kobayashi metric and can be induced by a Finsler form（see［8，16］）. The geodesic geometry of Teichmüuller metric was fully studied（see［1，5，6，11］and［12］，for example）.Recently，an approach to define the angles between two geodesics in a Teichmüuller space is given in［17］.It is proved that such angles always exists in a finite dimensional Teichmüuller space and the explicit formula of angles is obtained［17］.The existence and the formula of such angles between two geodesic rays in an infinite dimensional Teichmüuller space are discussed in［13，14］under some conditions as an application of their generalized main inequality of Reich-Strebel.The general existence and the formula of angles between two smooth geodesic segments in both finite and infinite dimensional Teichmüuller space are proved in［15］by using the Finsler form of Teichmüuller space.

The asymptotic Teichmüuller space AT（X）of X is an important relative of Teichmüuller space，which is defined as the space of asymptotic Teichmüuller equivalence classes where［µ］ATis the asymptotic Teichmüuller equivalence class containingµ.The asymptotic Teichmüuller equivalence～AThas the same definition as Teichmüuller equivalence with one exception that the mapping ϕ is allowed to be asymptotically conformal.A quasiconformal mapping ϕ：X→ϕ（X）is called asymptotically conformal if，for every ε＞0，there is a compact subset E of X such that the dilatation of ϕ outside E is less than 1+ε.

AT（X）is of meaning only when X is of infinite analytic type，otherwise，it is a single point. In what follows a Riemann surface is always assumed to be of infinite analytic type.

The asymptotic Teichmüuller space AT（X）was introduced by Gardiner and Sullivan［10］for the unit disk D，and by Earle，Gardiner，and Lakic［2-4］for the arbitrary hyperbolic Riemann surfaces（see［9］also）.It is known that there exist a complex Banach manifold structure and a natural metric，called the Teichmüuller metric on AT（X）.This metric can also be induced by a Finsler form.We refer to［4，7］for more informations on AT（X）.

In this article，the geometry of Teichmüuller metric in an asymptotic Teichmüuller space is studied.The structure of this article is as follows.Section 2 is devoted to set up the notation and the terminologies we need.In Section 3，the quotient Finsler structure on AT（X）is introduced and a binary infinitesimal form of Teichmüuller metric on AT（X）is obtained（see Theorem 3.2）.In Section 4，similar to that in Teichmüuller space T（X）［13-15，17］，the definition of the angles between any two geodesics with the same initial point in AT（X）is given.Furthermore，the existence and explicit formula are proved by Theorem 3.2.As an application，a sufficient condition to determine two different geodesics is obtained.

2　Preliminaries and Notation

In this section，we recall some definitions，notations，and basic results needed in this article. For more details，we refer to［4，9］.

In order to define the Teichmüuller metric on AT（X），we need the concepts of the boundary dilatation.For everyµ∈Belt（X），seth∗（µ）=inf｛‖ν‖∝：ν∈Belt（X）and ν−µvanishes at infinity｝.

Here，a Beltrami differentialµ∈Belt（X）is said to vanish at infinity，if for each ǫ＞0，there is a compact set E in X such that‖µ|X−E‖∝＜ǫ.For everyµ∈M（X），set

Then，

are called the boundary dilatations ofµand［µ］AT，respectively.

It is proved in［4］that

and the infimum of the above formulas can always be attained.We say thatµis asymptotically extremal in［µ］ATif h∗（µ）=h（µ）.

The asymptotic Teichmüuller distance dATof any two points［µ1］ATand［µ2］AT∈AT（X）is defined as

whereµis the Beltrami differential of the mapping fµ1◦（fµ2）−1.

Remark 2.1It seems that the above definitions of boundary dilatations are different from that in Chapter 14 of［9］.Indeed，it is easy to prove that they are the same.

Let Q（X）be the Banach space of integrable holomorphic quadratic differentials φ=φ（z）dz2on X with L1-norms

A sequence of quadratic differentials｛φn｝in Q（X）is said to be a degenerating sequence if‖φ‖=1 and φn→0 locally uniformly on X as n→∞.Denote by Qd（X）the set of all degenerating sequences.

The following theorem is the counterpart of Hamilton-Krushika´l-Reich-Strebel condition for asymptotically extremal Beltrami differentials.

Theorem 2.2（［9］）Letµbelong to M（X），thenµis asymptotically extremal in［µ］ATif and only if

For convenience，we denote

for everyµ∈M（X）.

Let Z denote the dual space of Q（X），which is naturally isomorphic to the tangent space of T（X）at its basepoint.Eachµin Belt（X）defines an element of Z by the formula

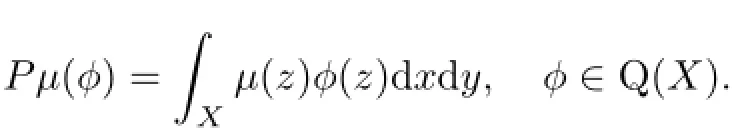
Let Belt0（X）be the subspace of Belt（X）whose elements vanish at infinity and let Z0be its image under the linear map P.

Let PZ0be the quotient map from Z to Banach spaceˆZ=Z/Z0，whereˆZ is naturally isomorphic to the tangent space of AT（X）at its basepoint.SetˆP=PZ0◦P，thenˆP：Belt（X）→ˆZ is the derivativeˆΦ′（0）of the quotient mapˆΦ at the basepoint.

Via the infinitesimal theory of asymptotic Teichmüuller space，for anyµ∈Belt（X），the natural quotient norm for the quotient Banach spaceˆZ have the following two equivalent form，

and

We say thatµ∈Belt（X）is infinitesimally asymptotically extremal if h∗（µ）=‖ˆPµ‖.From Theorem 2.2，for everyµ∈M（X），it is seen thatµis asymptotically extremal if and only ifµ is infinitesimally asymptotically extremal.

By the asymptotic inequalities for boundary dilatation corresponding to the Reich-Strebel inequalities，one have the following theorem.

Theorem 2.3（Asymptotic Teichmüuller contraction inequalities［4］）Ifµ∈M（X），then

3　The Teichmüuller Metric and Finsler Structure on AT（X）

It is known［4］that the Teichmüuller metric of AT（X）can be induced from the following Finsler structure：

that is，

whereµ，ν∈M（X）and σ∈Belt（X）.In particular，α is locally Lipschitz continuous，and consequently，it is continuous on the tangent bundle of the asymptotic Teichmüuller space AT（X）. For simplicity，denote the Teichmüuller metric on AT（X）by d.

The Finsler structure α on AT（X）has another representation［2］（see Chapter 14 of［9］also）：

where Xµ=fµ（X）.In particular，α（ˆΦ（0），ˆΦ′（0）ν）=H（ν）.The infinitesimal form of Teichmüuller metric on AT（X）is

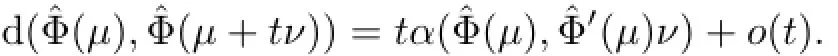
In the rest of this section，we are going to prove a binary infinitesimal form of Teichmüuller metric on asymptotic Teichmüuller space AT（X），corresponding to that on Teichmüuller space［15］.First，we need the following lemma which is a consequence of the asymptotic Teichmüuller contraction inequalities（Theorem 2.3）.

Lemma 3.1Suppose that Xtis a family of Riemann surfaces parameterized by t∈［0，t0］. If η（t）∈M（Xt）and η（t）=tδ（t）+o（t）as t→0+，where δ（t）∈Belt（Xt）and δ（t）=O（1）as t→0+，then

ProofFrom the definition of h∗，we have

Consequently，h（η（t））=O（t），t→0+，as h（η（t））≤h∗（η（t））.

By the asymptotic Teichmüuller contraction inequalities，we have

The left inequality of（3.5）implies

and the right inequality of（3.5）implies

As h∗（η（t））=O（t）and h（η（t））=O（t），then（h（η（t）））2=O（t2）and（h∗（η（t）））2=O（t2）as t→0+.Applying the Taylor expansion to（3.6）and（3.7），we obtain

Thus，

Therefore，

This completes the proof of Lemma 3.1.

In order to get the binary infinitesimal form of Teichmüuller metric on AT（X），we need some notions.

For fixedµ∈M（X），let ρµbe the map from M（X）to M（Xµ）such that fρµ（ν）=fν◦（fµ）−1for all ν in M（X），where Xµ=fµ（X）.Then，ρµ：νρµ（ν）is biholomorphic and

There exists a well-defined biholomorphic mapˆρµ：AT（X）→AT（Xµ）such that the diagram

commutes.

As ρµis an isometry and the Teichmüuller Finsler structures on AT（X）and AT（Xµ）are the quotient structures induced byˆΦ andˆΦµ，it follows readily thatˆρµis an isometry with respect to these structures.So，the maps ρµandˆρµare called geometric isomorphisms.

A continuous curveµ（t）（t∈［0，t0））in M（X）is said to be differentiable at 0 if there exists someµ∈Belt（X）such thatµ（t）=µ（0）+tµ+o（t）as t→0+.µis called the derivative ofµ（t）at 0 and denoted byµ′（0）.

Theorem 3.2Letµ（t）and ν（t）be two continuous curves from［0，t0］into M（X）which are differentiable at 0 and satisfyµ（0）=ν（0）.Then，

ProofFirst，we prove（3.10）in the case ofµ（0）=ν（0）=0.

Let η（t）=ρν（t）（µ（t）），namely，

Asµ（t）and ν（t）are differentiable at 0，we have

and consequently，

Set Xt=Xν（t），then η（t）∈M（Xt）satisfies the assumption of Lemma 3.1 with

Thus，by Lemma 3.1，we have

From（3.3），it can be obtained that

The continuity of the Finsler structure α on AT（X）yields

Consequently，by（3.11），we have

Asˆρν（t）：AT（X）→AT（Xt）is an isometry and，so

and（3.10）follows.

Now，we prove（3.10）for general case.

Let ρµ（0）be the geometric isomorphism from M（X）to M（Xµ（0））and˜µ（t）be the Beltrami coefficient of fµ（t）◦（fµ（0））−1，namely，

By the differentiability ofµ（t），we obtain

Similarly，the Beltrami coefficient˜ν（t）of fν（t）◦（fµ（0））−1has the following form

Clearly，˜µ（t）and˜ν（t）are differentiable at 0 and˜µ（0）=˜ν（0）=0.Applying the above proved result for the special case to X0=Xµ（0），˜µ（t）and˜ν（t），and by（3.3）again，we get

and（3.10）follows.

4　Angles in the Asymptotic Teichmüuller Space AT（X）

A geodesic in AT（X）is a continuous curve which is locally shortest with respect to the Teichmüuller metric.Every geodesic curve in AT（X）can be represented as γ（t）=ˆΦ（µ（t））：［0，1］→AT（X），whereµ（t）：［0，1］→M（X）is a continuous curve in M（X）.

Let α and β be geodesics in AT（X）with the same initial point.Then，by choosing parts of them and by reparameterizing，they can be，respectively，represented asˆΦ（µ（t））andˆΦ（ν（t））（t∈［0，δ））such that d（ˆΦ（µ（0）），ˆΦ（µ（t）））=d（ˆΦ（ν（0）），ˆΦ（ν（t）））（t∈［0，δ）），whereµ（t）and ν（t）are continuous curves in M（X）andµ（0）=ν（0）.Then，the angle θ between this two geodesics α and β at pointˆΦ（µ（0）））is defined by the following equation

if the limit exists.

Ifµ∈M（X）is asymptotically extremal，then γµ（t）=［tµ/‖µ‖∝］AT，t∈（−1，1）is a geodesic.As the infimum in the definition of h∗（µ）can always be achieved，there is another asymptotically extremal Beltrami differential ν∈M（X）such thatµ−ν vinishes at infinity and‖ν‖∝=h∗（µ）.So，γν（t）=［tν/‖ν‖∝］AT，t∈（−1，1）and γµrepresent the same geodesic passing through［0］ATand［µ］AT.

Letµ∈Belt（X）and‖µ‖∝=1.We say thatµis asymptotically extremal if kµis asymptotically extremal for some k∈（0，1）.It is clear that ifµis asymptotically extremal，tµ is also asymptotically extremal for any t∈（−1，1）.

Without loss generality，suppose thatµ∈Belt（X）is asymptotically extremal with‖µ‖∝= h∗（µ）=1.Then，the curve γµ（t）=［tµ］AT：（−1，1）→AT（X）is a geodesic line and γµ（t）|［0，1）is a geodesic ray from the basepoint［0］ATdetermined byµ.It is clear that

Letµand ν be two asymptotically extremal Beltrami differentials on X with‖µ‖∝= h∗（µ）=1 and‖ν‖∝=h∗（ν）=1.Then，γµand γνare two geodesic rays and

The following result，which follows from Theorem 3.2 directly，shows the existence of angles between two geodesic rays in AT（X）.

Theorem 4.1Let X be any hyperbolic Riemann surface.Suppose thatµ，ν∈Belt（X）are asymptotically extremal with‖µ‖∝=h∗（µ）=1 and‖ν‖∝=h∗（ν）=1.Then，the angle θ between γµand γνexists and

Letµ，ν∈M（X）be two asymptotically extremal Beltrami differential in［µ］AT∈AT（X），then［tµ］ATand［tν］AT，（0≤t≤1）are two geodesic segments joining［0］ATand［µ］AT，but we do not know whether they are different or not.By Theorem 4.1，we get a sufficient condition to determine when this two geodesic segments are different.

Corollary 4.2Letµand ν be two asymptotically extremal Beltrami differentials in M（X）｛0｝and［µ］AT=［ν］AT.If

then the two geodesics［tµ］ATand［tν］AT（0≤t≤1）are different.

ProofBy hypothesis，［tµ］ATand［tν］AT（t∈［0，1］）are two geodesic segments joining［0AT］and［µ］AT.By the definition of h∗，there exist˜µand˜ν in M（X）such thatµ−˜µand ν−˜ν vanish at infinity and

As φn∈Qd（X）is a degenerating sequence，is a compact subset of X.We have

for any compact subset E in X.As（µ−ν）−（˜µ−˜ν）vanishes at infinity，so by（4.3），

Let λ1=˜µ/‖˜µ‖∝and λ2=˜ν/‖˜ν‖∝.Then，λ1and λ2satisfy the condition of Theorem 4.1.So，the angle θ between two geodesic rays γλ1and γλ2exists and

It is clear that H（˜µ−˜ν）＞0 implies H（λ1−λ2）＞0.Thus θ 6=0，and consequently，［tµ］ATand［tν］ATare different geodesic segments.

Remark 4.3Corollary 4.2 is previously known only for the case that X is the unit disk D（［7］）.Here，we prove it for the asymptotic Teichmüuller space AT（X）of any general Riemann surface X of infinite analytic type by a new approach.

By the geometric isomorphisms ρµ0：M（X）→M（Xµ0）andˆρµ0：AT（X）→AT（Xµ0）mentioned in Section 3，we give the definition of standard geodesic segment between any two points［µ0］ATand［µ］ATin AT（X）.

When ρµ0（µ）is asymptotically extremal in［ρµ0（µ）］AT，the curve

is the part of a geodesic ray between［0］ATand［ρµ0（µ）］ATin AT（Xµ0），where τ=∂fµ0/∂fµ0. Pulling-back this curve to AT（X）by the geometric isomorphismˆρµ0，we get a geodesic segment joining

We call this geodesic segment standard.Moreover，

Then，the following theorem comes from Theorem 3.2.

Theorem 4.4Letµ0，µ1，andµ2be three Beltrami coefficients in M（X）such thatare asymptotically extremal.Then，the angle θ at the pointbetween the standard geodesic segments γµ0，µ1and γµ0，µ2exists and

ProofLet

and

As fµ1◦（fµ0）−1and fµ2◦（fµ0）−1are asymptotically extremal，ˆΦ（µ（t））andˆΦ（ν（t））are standard geodesic segments γµ0，µ1and γµ0，µ2，respectively.

It is clear thatµ（t）and ν（t）satisfy the condition of Theorem 3.2.So by Theorem 3.2 and（4.4），we have

The proof of Theorem 4.4 is completed.

From the proof of Theorem 4.4，it is clear that the following more general theorem is also true.

Theorem 4.5LetˆΦ（µ（t））andˆΦ（ν（t））（t∈［0，t0］，0＜t0＜1）be two geodesic segments in AT（X），whereµ（t）and ν（t）：［0，t0］→M（X）are continuous curves in M（X）with the same initial pointµ（0）=ν（0），which are differentiable at 0 and

Then，the angle θ atˆΦ（µ（0））betweenˆΦ（µ（t））andˆΦ（ν（t））exists，and

To end this article，we emphasize that the geodesic segments in Theorem 4.5 need not to be standard.

References

［1］Earle C J.The Teichmüuller distance is differentiable.Duke Math J，1977，44：389-397

［2］Earle C J，Gardiner F P，Lakic N.Teichmüuller spaces with asymptotic conformal equivalence.No.IHESM-95-60.SCAN-9507105，1994

［3］Earle C J，Gardiner F P，Lakic N.Asymptotic Teichmüuller space.Part I：The complex structure，Contemporary Math，2000，256：17-38

［4］Earle C J，Gardiner F P，Lakic N.Asymptotic Teichmüuller space.Part II：The metric structure，Contemporary Math，2004，355：187-219

［5］Earle C J，Kra I，Krushkal′S L.Holomorphic Motions and Teichmüuller spaces.Trans Amer Math Soc，1994，343：927-948

［6］Earle C J，Li Z.Isometrically ebmbeded polydisks in infinite-dimensional Teichmüuller spaces.Journal of Geometric Analysis，1999，9：51-71

［7］Fan J H.On geodesics in asymptotic Teichmüuller spaces.Math Z，2011，267：767-779

［8］Gardiner F P.Teichmüuller Theory and Quadratic Differentials.New York：John Wiley Sons，1987

［9］Gardiner F P，Lakic N.Quasiconformal Teichmüuller Theory.New York：American Mathematical Society，2000

［10］Gardiner F P，Sullivan D P.Symmetric structures on a closed curve.Amer J Math，1992 114：683-736

［11］Li Z.Non-uniqueness of geodesics in infinite dimensional Teichmüuller spaces.Complex Var Theory Appl，1991，16：261-272

［12］Li Z.Non-uniqueness of geodesics in infinite dimensional Teichmüuller spaces（II）.Ann Acad Sci Fenn，Ser A I Math，1993，18：335-367

［13］Li Z，Qi Y.Fundamental Inequalities of Reich-Strebel and Triangles in a Teichmüuller spaces.Contempory Mathematics，2012，57：283-298

［14］Li Z，Qi Y.Angles between two geodesic rays in a Teichmüuller spaces（To appear）

［15］Hu Y，Shen Y L.On angles in Teichmüuller spaces.Math Z，2014，277：181-193

［16］Royden H L.Report on the Teichmüuller metric.Proc Amer Math Soc，1970，65：497-499

［17］Yao G W.A binary infinitesimal form of Teichmüuller metric.Preprint，arXiv：0901.3822

April 22，2015.This work was supported by National Natural Science Foundation of China（11371045，11301248）.