边界约束对膨胀土干缩开裂的影响*
2016-09-26谢锦宇
袁 权 谢锦宇 任 柯
(①西华大学建筑与土木工程学院 成都 610039)
(②西南民族大学国有资产处 成都 610041)
边界约束对膨胀土干缩开裂的影响*
袁权①谢锦宇①任柯②
(①西华大学建筑与土木工程学院成都610039)
(②西南民族大学国有资产处成都610041)
膨胀土是岩土工程中常见的一类特殊土,具有失水收缩和吸水膨胀的变形特征,如何量化收缩变形及其与干缩裂缝之间的关系是土工建筑物稳定性和安全性评估的基本问题。本文利用Bishop有效应力原理和广义胡克定律证明了采用含水率或基质吸力为基本变量的两种分析方法的等价性。把岩土工程中常用的原状土收缩实验中测量的收缩系数与收缩应变关联,得到了土体两端存在和没有位移约束时的总水平应力及其与含水率分布之间的关系。结果表明,无边界位移约束时,收缩变形的不均匀性小,应力水平低,且含水率对应力分布的影响小;存在约束时,收缩变形将受到限制,易诱发干缩裂缝,其深度受土体弹性模量和收缩系数的影响。
膨胀土收缩变形干缩裂缝含水率总水平应力
0 引 言
膨胀土是公路、铁路和建筑等工程中较常遇到的一类特殊土。随着含水率的增加或减小,具有明显膨胀或收缩的变形特征。在膨胀土脱水干燥过程中,如果收缩变形不均匀或变形受到限制,土体表面常出现网状裂缝和龟裂现象。这些干缩裂缝将使土体的完整性破坏,强度降低,影响工程结构物的完全使用(杜海民等,2015)。因此,必须对干缩裂缝的发育程度和发展趋势进行准确的评估,才能采取有效的预防措施。
对于土体在自然环境下的开裂深度,《膨胀土地区建筑技术规范》(中华人民共和国行业标准编写组,2012a,2012b)列举了多种定性分析方法,如膨胀率和大气影响深度等。要具体考虑相关因素对干缩裂缝的影响,还须采用定量分析方法。郑少河等(2007)运用线弹性断裂力学理论分析了半无限体在多种荷载作用下裂缝的深度和间隔问题,但没有考虑土中水和气的影响。Fredlund et al.(1993)采用基质吸力沿土层深度线性变化的假设估算了K0条件下土体张拉裂缝的深度。Morris et al.(1992)、郑少河等(2006)和孙即超等(2009)结合Fredlund的方法分别计算了非饱和土在稳定渗流和K0条件下的开裂深度。这类研究建立在稳定渗流,土体自重影响和K0条件下,但实际情况可能更复杂。当地下水位很深或上部土层供水不足时,土中水和气随时变化,基质吸力沿土深并非线性分布;K0条件建立在水平应变为零基础上,而土体在其侧向有时并无位移约束,即使在侧限条件下,由于土体在边界处先脱黏,侧向变形是自由的;土层较薄时,自重很小,更容易产生贯穿整个深度的裂缝。另一类研究是采用类似热应力的分析方法,引入收缩应变和考虑土中水的分布来分析膨胀土干缩开裂问题。Peron et al.(2009)利用土条干缩实验研究了膨胀土收缩变形的一维问题。Toga et al.(2006)研究了圆盘土样在稳定渗流和蒸发条件下其干缩裂缝的长度及角度问题。吴珺华等(2011)基于收缩变形对膨胀土的初始开裂进行了分析。需指出,以上关于膨胀土干裂的研究均没有考虑边界约束对裂缝的影响。鉴于干缩裂缝产生的物理机制,同时考虑土体收缩变形的不均匀性和边界约束情况才能对土体干缩开裂有更深入的了解。本文采用收缩应变概念和Fredlund方法分析了蒸发条件下土体的边界约束情况对干缩裂缝的影响。
1 应力分析
1.1收缩变形
膨胀土失水变干时,含水率的减小伴随着基质吸力的增大进而引起收缩变形。基质吸力的变化影响有效应力但不影响总应力的变化。蒸发条件下,土中水,水到气的转化机理以及它们的迁移过程都非常复杂,不易测得基质吸力的分布,这就限制了Fredlund方法的适用范围。膨胀土的开裂条件是净水平应力是否达到土体的抗拉强度。当收缩变形受到约束或变形不均匀时,土体的总应力增大,也会达到开裂条件。所以,可从变形的角度出发,利用类似热应力的分析方法来研究膨胀土中的应力状态。Peron et al.(2009)曾指出,可把总应变分解为机械应变和收缩应变之和
(1)
上式中的收缩应变定义在体积应变基础上,与含水率和湿涨缩系数联系在一起。吴珺华等(2011)把收缩应变表示为:
(2)
其中,α、w和wcr分别为湿涨缩系数、含水率和临界含水率。实际上,也可从有效应力和广义胡克定律导出收缩应变的表达式。Bishop有效应力表示为(Fredlund et al.,1993; Lu et al.,2012):
(3)
其中,σij为总应力;ua为孔隙气压;(ua-uw)为基质吸力;δij为Kronecker符号。在线弹性范围内,非饱和土的广义胡克定律描述了总应变与有效应变之间的关系:
(4)
其中,G、E和ν分别为土体的剪切模量、弹性模量和泊松比。把式(3)代入式(4)可得:
(5)
从上式可以看出,总应变可表示为两项之和,其中一项与总应力相关,即机械应变,另一项与基质吸力相关,即收缩应变。对比式(1)、式(2)和式(5)可得收缩应变:
(6)
比如,土体干缩开裂主要考虑水平方向的应变,其表达式为:
(7a)
(7b)
从上式可以看出,采用与含水率相关的收缩应变或基质吸力为基本变量来分析土中应力分布是等价的。需要说明的是,式(7b)中的收缩应变系数表示单位长度的土体每失去1个百分比的含水率的缩短,也就是收缩系数,可由原状土的收缩实验确定。图1a和图1b分别显示了土体干燥全过程中体积变化和原状土含水率和线缩率关系曲线的示意图。从图1a可以看出,在膨胀土收缩过程中的第Ⅰ阶段,即流动和塑性阶段,土的体积变形与含水率之间呈线性关系,适合定义收缩应变系数。恰好膨胀土易在塑性阶段萌生裂缝。从图1b可以看出,虽然在收缩实验中,原状土的初始含水率可能小于wP,但其线缩率与含水率之间也存在线性关系,由此,可定义收缩应变系数就是收缩系数:
(8)

图1 膨胀土的收缩系数测量Fig.1 Shrinkage coefficient of swelling soila.土体收缩过程; b.含水率vs.收缩率
而且,结合图1a,可假设图1b中的斜直线段可延长到塑性阶段,即认为由原状土收缩实验测得的收缩系数也适用于塑性阶段。下面将在式(5)的基础上讨论边界约束情况对膨胀土收缩开裂的影响。
1.2总水平应力分析
膨胀土在蒸发条件下的开裂深度是核心问题,为了对其进行有效评估,必须考查净水平应力沿厚度方向的分布情况。如图2所示,在自然蒸发条件下,相比水平方向,含水率沿厚度方向变化更大,对净水平应力的分布影响更大,可假设同层土中含水率相同。这样,可把由于含水率的变化产生的收缩变形以及边界约束引起的应力变化简化为平面应变问题。此时,需要把E、ν和α替换为:
(9)

图2 膨胀土的几何尺寸Fig.2 Geometry of swelling soil
考虑到计及自重影响的平衡微分方程,几何方程和物理方程式(5),引入收缩变形的艾力应力函U(x,z),只要其满足:
(10)
以及边界条件,就能获得此问题的解答。总水平应力可用艾力函数表示为:
(11)
由于w仅是z的函数,可直接对式(11)两边同时积分两次得到:
(12)
其中A和B分别为积分常数,由边界条件确定,以土体两端x=±L处是否存在位移约束来讨论。
如果在x=±L两端无位移约束,收缩变形是自由的,土体纵截面上无轴力和弯矩,即
(13)
把式(12)代入式(13),计算后得到:

确定出积分常数A和B后,回代入式(12),即可得无边界约束时的总水平应力。
如果土体两端有约束作用,即在x=±L处,有u|x=±L=0。 此时,土体纵截面上弯矩为零,但轴力不为零。实际上,两端的位移约束限制了土体的收缩变形,即εx=0。直接利用式(7a),令其等于零,注意到平面应变时存在材料常数替换的式(9),总水平应力可表示为:
(14)
其中总竖向应力由土体自重引起,σz=ρd(1+w) gz,ρd为土颗粒的干密度,g为重力加速度。
2 讨 论
含水率的分布和边界约束情况对收缩变形和总水平应力有重要影响。考虑4种典型的含水率分布,如图3所示,情形①~④分别为均匀分布、线性分布、抛物线分布和双曲线分布,对应的含水率表达式为:
①w(z)=wcr,
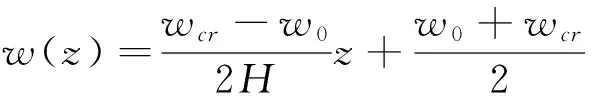



图3 4种典型的含水率分布Fig.3 Four typical distributions of water content
膨胀土的物理参数取自已出版的文献(姚海林等,2004;吴珺华等,2011):w0=10%,wcr=24%,E=6MPa,ν=0.3,α=0.1,2H=5m。把含水率的分布代入式(12)或式(14)就能得到存在或没有位移约束时的总水平应力。经计算,当土体边界无约束且含水率分布为情形①和②时,土体的收缩变形是均匀的,内部总水平为零。图4显示了含水率分布为情形③和④时的总水平应力分布。从中可以看出,土体边界无约束时,土中既有拉应力和压应力,但其数值很小。相反地,土体两端的边界位移约束对总水平应力的影响很大,除了含水率的分布①外,其他3种含水率分布均使土体内部产生较大的水平拉应力。由于土体的抗拉强度低,可用拉应力的分布范围来判断干缩裂缝的深度。姚海林等(2004)对处于丘陵地带的某2级公路旁的膨胀土进行了原位观测,其厚度约为5m,发育有一深度为3.6m的竖向裂缝。用Fredlund方法估算的开裂深度为3.7m,结果与实际裂缝深度接近。考虑含水率分布情形③和④,采用式(14)计算得到的裂缝深度分别为3.25m和4m,与实际开裂深度接近,说明采用本文的分析方法具有一定的可靠性。
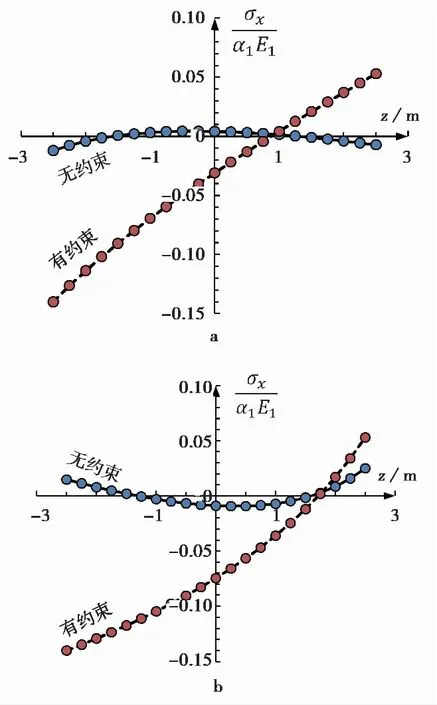
图4 总水平应力分布Fig.4 Distribution of total horizontal stressa.含水率为抛物线分布; b.含水率为双曲线分布
含水率的非线性分布将使土体产生非均匀的收缩变形,如果收缩变形受到限制,土体内部产生附加的拉应力,一旦此拉应力大于土压力,易诱发干缩开裂。对于工程中常用的砂土,其孔隙大且连通性好,含水率在一定深度范围内成线性分布(Lu et al.,2012),则出现水平拉应力的几率小,也就不易开裂。而对于粉土和黏土等膨胀土,孔隙小且连通性差,含水率一般呈非线性分布,由此引起的收缩变形受到限制或土体较宽(意味着L较大,εx=0),土体易开裂。即使无位移约束,与图4描述的情况一样,由于非均匀收缩,土体表面也产生较小的拉应力,这可解释开裂后的土体表面会出现深度较浅的短裂缝。
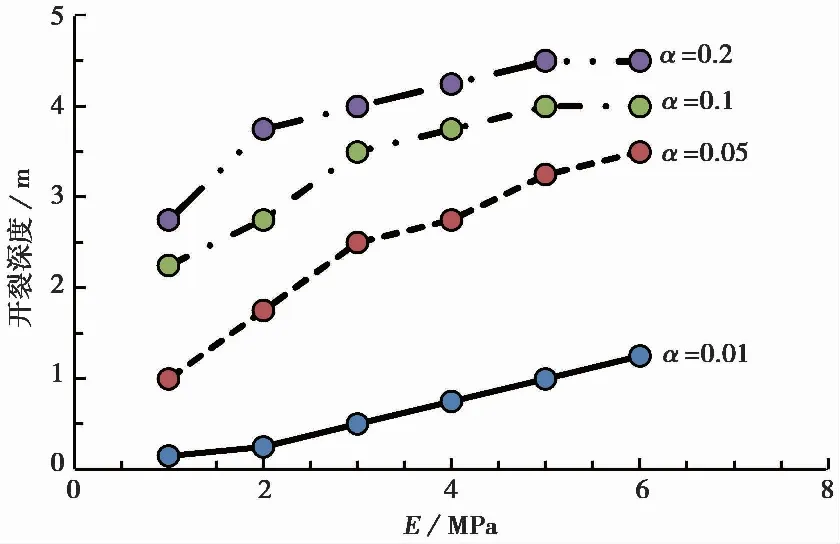
图5 干缩裂缝的深度与E和α间的关系Fig.5 Depth of desiccation crack vs.E and α
同时,在式(14)中令总水平应力等于零(忽略孔隙气压),即σx=0,则能得到不同含水率时的开裂深度。图5显示了弹性模量和收缩应变系数对开裂深度的影响。存在边界位移约束时,干缩裂缝的深度随着E和α的增大而增大。根据胡克定律,大的弹性模量会增大附加拉应力,被限制的收缩变形一定时,弹性模量的增大会减小总水平应力的大小和增大拉应力分布的范围,从而使开裂深度和宽度增大。大的收缩应变系数意味着大的收缩变形,当变形受到限制时,也会提升总水平应力,干缩裂缝的深度增大,而且α的影响更大。可采用减小α的措施来防止裂缝萌生和扩展。比如,在地表覆盖遮挡物或排出土中下层水以使含水率的分布均匀化。还可在土体中掺入纤维来增大抗拉强度来减小开裂几率。基质吸力的分布不易确定,相比之下,含水率不难量测,本文提出的分析膨胀土应力分布的方法更便于工程应用。但注意到,膨胀土的干缩开裂涉及到复杂的物理过程,分析时应考虑塑性变形、蒸发条件下的含水率变化、应力重分布及开裂判据等,对此,本文提出的简单方法有待进一步扩展。
3 结 论
针对膨胀土失水变干过程中的收缩变形,本文通过总水平应力分析了含水率分布和边界约束情况对土体干缩开裂的影响,得出如下结论:
(1)当土体两端无位移约束时,含水率分布对土中总水平应力影响不大。若考虑土体具有一定的抗拉强度,不管含水率分布如何,几乎不产生干缩裂缝。
(2)当土体两端存在位移约束时,由于收缩变形受到限制,土体上层将出现拉应力,已引起干缩裂缝,其深度受弹性模量和收缩应变系数的影响,后者尤甚。
(3)可采取减小收缩应变系数的方法来防止裂缝的发生和发展。
Du H M,Ma W,Zhang S J.2015.Effects of strain rate and water content on failure strain energy density of frozen soil[J].Journal of Engineering Geology,23(Sl):38~43.
Fredlund D G,Rahardjo H.1993.Soil mechanics for unsaturated soils[M].New York:John Wiley & Sons,298~301.
Lu N,William J L.2012.Unsaturated Soil Mechanics[M].Beijing:Higher Education Press,214~215.
Morris P H,Graham J,Wiliams D J.1992.Cracking in drying soils[J].Canadian Geotechnical Journal,29(2):263~267.
Peron H,Delenne J Y,Laloui L,et al.2009.Discrete element modelling of drying shrinkage and cracking of soils[J].Computers and Geotechnics,36(1-2):61~69.
Ran L Z,Song X D,Tang C S.2011.Laboratorial investigation on tensile strength of expansive soil during drying[J].Journal of Engineering Geology,19(4):620~625.
Sun J C,Wang G Q,Sun Q C.2009.Crack spacing of unsaturated soils in the critical state[J].Chinese Science Bulletin,54(9):1311~1314.
Tang C S,Shi B,Liu C.2012.Study on desiccation cracking behaviour of expansive soil[J].Journal of Engineering Geology,20(5):663~673.
The Professional Standards Compilation Group of People’s Republic of China.2012a.Technical code for buildings in expansive soil regions GB 50112-2013 [S].Beijing:China Architecture & Building Press.
The Professional Standards Compilation Group of People’s Republic of China.2012b.Code for special soil and rock investigation of railway engineering TB 10038-2012 [S].Beijing:China Railway Publishing House.
Toga K B,Alaca B E.2006.Junction formation during desiccation cracking[J].Physical Review E statistical nonlinear and soft matter physics,74(1):79~97.
Wu J H,Yuan J P,Lu T H.2011.Analysis of initial cracking behavior of expansive soil due to moisture change stress[J].Rock and Soil Mechanics,32(6):1631~1636.
Yao H L,Cheng P,Wu W P.2004.A simplified method for predicting heave in expansive soil grounds based on three dimensional shrinkage tests[J].Rock and Soil Mechanics,25(11):1688~1692.
Zheng S H,Jin J L,Yao H L.2006.Analysis of initial cracking behavior of expansive soil due to evaporation[J].Rock and Soil Mechanics,27(12):2229~2233.
Zheng S H,Yao H L,Ge X R.2007.Mechanical analysis on cracking behavior of expansive soil due to climatic condition[J].Shanghai Geology,(2):29~32.
杜海民,马巍,张淑娟.2015.应变率和含水率对冻土破坏应变能密度影响特性试验研究[J].工程地质学报,23(增刊):38~43.
卢宁,William J L.2012.非饱和土力学[M].北京:高等教育出版社:214~215.
冉龙洲,宋翔东,唐朝生.2011.干燥过程中膨胀土抗拉强度特性研究[J].工程地质学报,19(4):620~625.
孙即超,王光谦,孙其诚.2009.临界状态下非饱和土裂缝开裂间距[J].科学通报,54(9):1311~1314.
唐朝生,施斌,刘春.2012.膨胀土收缩开裂特性研究[J].工程地质学报,20(5):663~673.
吴珺华,袁俊平,卢延浩.2011.基于变湿应力概念的膨胀土初始开裂分析[J].岩土力学,32(6):1631~1636.
姚海林,程平,吴万平.2004.基于收缩实验的膨胀土地基变形预测方法[J].岩土力学,25(11):1688~1692.
郑少河,金剑亮,姚海林,等.2006.地表蒸发条件下的膨胀土初始开裂分析[J].岩土力学,27(12):2229~2233.
郑少河,姚海林,葛修润.2007.气候影响下膨胀土开裂的力学分析[J].上海地质,102(2):29~32.
中华人民共和国行业标准编写组.2012a.膨胀土地区建筑技术规范(GB 50112-2013)[S].北京:中国建筑工业出版社.
中华人民共和国行业标准编写组.2012b.铁路工程特殊岩土规程(TB 10038-2012)[S].北京:中国铁道出版社.
EFFECT OF BOUNDARY CONSTRAINS ON DESICCATION CARCK OF SWELLING SOIL
YUAN Quan①XIE Jinyu①REN Ke②
(①College of Architecture and Civil Engineering,Xihua University,Chengdu610039)
(②Stated-owned Assets Management Bureau,Southwest University for Nationalities,Chengdu610041)
Swelling soil is a special soil often encountered in geotechnical engineering.It is of classic drying shrinkage and water swelling characteristics due to the moisture change in soil.How to quantify the shrinkage deformation and its relationship with desiccation crack is important issue in assessment of the stability and security of earth structures.The analysis based on distribution of water content is proved to be equivalent of that base on matric suction by Bishop’s effective stress and generalized Hooke’s Law.The shrinkage coefficient measured by shrinkage test of undisturbed soil sample can be associated with shrinkage strain.The total horizontal stress and its relationship with the distribution of water content is obtained with or without consideration of boundary displacement constrains.The results show that the non-uniform of shrinkage deformation and stress level is small and little desiccation cracks will be produced when there are no boundary constrains in soil.But if the displacement constrains are imposed at the ends of soil body,shrinkage deformation can be restrained and desiccation cracks can be produced.The depth of desiccation crack is strongly influenced by Young’s modulus and shrinkage coefficient of soil.
Swelling soil,Shrinkage deformation,Desiccation cracks,Water content,Total horizontal stress
10.13544/j.cnki.jeg.2016.04.015
2015-07-17;
2015-11-07.
教育部“春晖计划”合作科研项目(Z2014040),西华大学重点科研项目(z1320608)资助.
袁权(1982-),男,博士,主要从事断裂力学和非饱和干缩开裂方面的研究工作.Email:yuanqxh@163.com
TU43
A
