多目标群体博弈中弱Pareto完美平衡点
2016-09-24杨光惠
陈 莎,杨 辉,杨光惠
(贵州大学 理学院, 贵州 贵阳 550025)
多目标群体博弈中弱Pareto完美平衡点
陈莎,杨辉*,杨光惠
(贵州大学 理学院, 贵州 贵阳 550025)
基于有限理性下多目标群体博弈平衡点的精炼, 提出弱Pareto完美平衡点的概念。首先, 应用向量值Ky Fan不等式证明一般情形下多目标群体博弈中的弱Pareto-Nash平衡点的存在性。 其次, 给出弱Pareto完美平衡点的存在性。
多目标群体博弈;Ky Fan不等式; 弱Pareto-Nash平衡点; 弱Pareto完美平衡点
由大量行动的思想发展而来的群体博弈理论现已成为博弈论的一个重要的研究方向。 它所描述的是在由一个或多个群体构成的社会中, 每个群体中大量个体进行策略选择而形成一个社会状态, 个体希望自身收益最大, 而全局考虑希望社会稳定的这样一个博弈问题。 群体博弈理论的核心概念仍然是Nash平衡, 即给定关于每种社会状态的支付函数, 考虑在哪些社会状态下, 个体均没有动机去改变当前所选策略, 从而达到社会和谐稳定。 在一般非合作博弈中对Nash平衡点的研究已涌现了许多经典的结果, 但在群体博弈中却可见不多。
1950-1951年, Nash[1,2]在其开创性论文中介绍了n人有限非合作博弈模型, 引入了平衡点的定义并证明其存在性(后来被称为Nash平衡)。 这种基于局中人完全理性前提下得到的 Nash平衡点并不唯一, 这困扰着对平衡点的选取, 因此学者们提出了平衡点的精炼以剔除某些不合理的平衡点。在20世纪50年代后期, 学者们围绕着Nash平衡点的精炼开展了许多博弈论有限理性的相关研究, 并得到了不少重要成果[3-5]。
1959年, Shapley提出多目标博弈平衡点的概念[6], 之后相继涌现出多目标非合作博弈解的不少概念及其存在性等相关结果[7-9], 当前多目标非合作博弈的弱Pareto-Nash平衡点仍是研究热点。 对于多目标群体博弈而言, 其最新结果为文献[10]中给出的多目标群体博弈的弱Pareto-Nash平衡点概念及其存在性, 我们注意到在该文中仅考虑双目标单群体情形, 而更为一般的情形应该是多目标多群体的博弈问题, 但相关结果并不多见。 因此, 多目标多群体博弈的弱Pareto-Nash平衡更具有研究价值。
本文就多目标群体博弈模型考虑多个群体下,每个群体有多于两个目标且每个群体目标数相异情形下的弱Pareto-Nash平衡点的存在性, 并且基于有限理性考虑平衡点的精炼, 进一步提出弱Pareto完美平衡点的概念并证明其存在性。
1 基础知识
多目标群体博弈模型描述如下[11]:
记P={1,2,…,p0}为社会集, 表示该社会由p0个群体组成。 每个群体p∈P由充分多但有限个(在统计意义上)个体组成, 设为mp个。
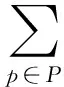
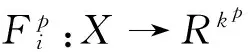

其中
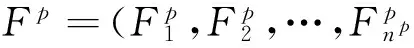
记上述多目标群体博弈为MG=(X,F)。
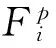
对任意的正整数m, Rm为m维欧氏空间。
记集合
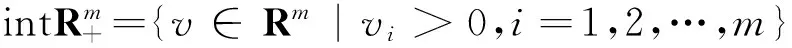
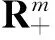
定义1.1[12]设a,b∈Rm,
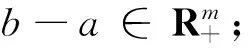
(2)ab⟺
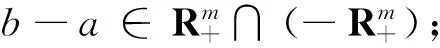
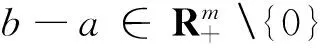
下面给出向量值函数的连续性和凸性的定义及相关结果, 参见文献[13]。
定义1.2设X是Rn中的一个非空子集,f:X→Rk是一个向量值函数,x∈X, 如果对Rk中零点0的任何开邻域V, 存在x在X中的任何开邻域O(x),使得∀x′∈O(x), 有
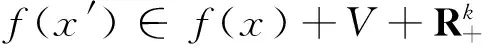

注1.2若k=1, 则f是实泛函, R+-连续即是实泛函中的下半连续。
定义1.3设X是Rn中的一个非空凸集,f:X→Rk是一个向量值函数。
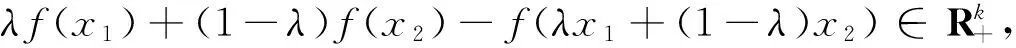

(2) 如果∀x1,x2∈X,∀λ∈(0,1), 有
λf(x1)+(1-λ)f(x2)=f(λx1+(1-λ)x2),
则称向量值函数f在X上是仿射的。

根据上述定义易证下面的命题。
命题1.1设向量值函数f,g:X→Rk,
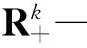
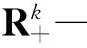
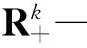
下面是重要的向量值KyFan不等式定理。
引理1.1(向量值KyFan不等式)设X是Rn中的非空有界闭凸集, 向量值函数φ:X×X→Rk满足:
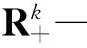
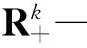
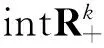
2 弱Pareto-Nash平衡点
下面将给出多目标群体博弈的弱Pareto-Nash平衡点的定义及其存在性。
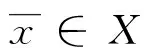
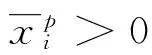
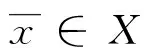
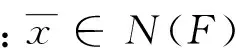
定理2.1具有连续向量值支付函数的多目标群体博弈MG的弱Pareto-Nash平衡点必存在。
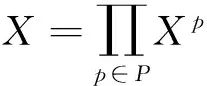
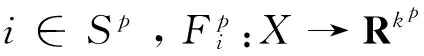
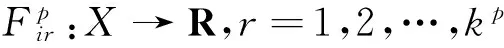
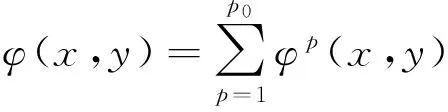
其中
φp(x,y)
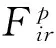
∀y∈X,r=1,2,…,kp, 有
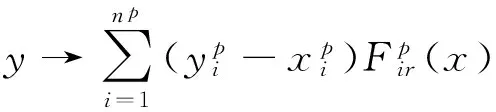

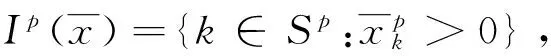
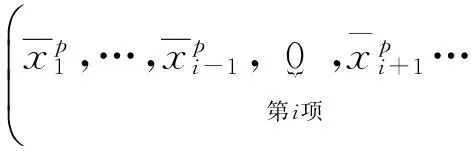
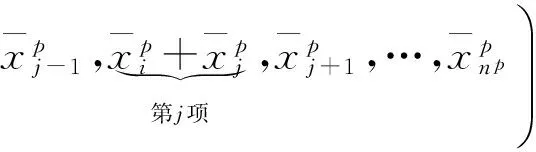
则
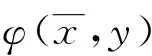
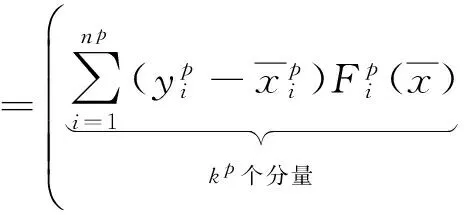


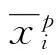
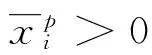
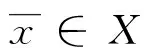
3 弱Pareto完美平衡点
基于Selten提出的完美平衡点的思想, 在有限理性下研究群体博弈时, 我们考虑并非所有个体都能完全理性地选择好的策略, 即使某些策略并不是最好的, 但还是有极少的个体去选择, 因此, 利用状态空间的微小扰动来描述这种有限理性。设ε>0足够小(满足mpε<1), ∀p∈P,
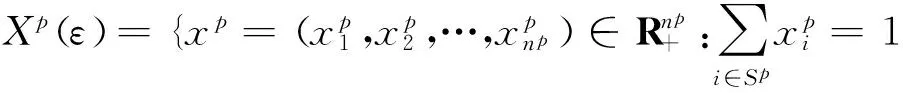
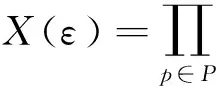
记MG(ε)=(X(ε),F)为扰动多目标群体博弈。在下面的博弈模型MG=(X,F)中,X为完全混合状态空间, 即∀p∈P,
下面给出弱Pareto完美平衡点的概念及其存在性。
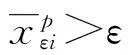
注3.1MG(ε)的弱Pareto-Nash平衡点一定是MG的ε-弱Pareto完美平衡点。
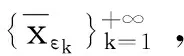
定理3.1具有连续向量值支付函数的多目标群体博弈MG的弱Pareto完美平衡点必存在。
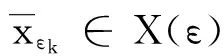
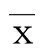
∀p∈P,∀i∈Sp,存在j∈Sp,若
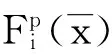
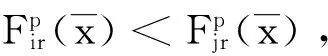
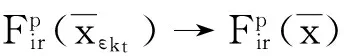
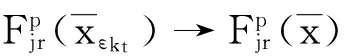
所以

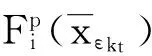
[1] Nash J. Non-Cooperative Games[J]. The Annals of Mathematics, 1951, 54(2): 286-295.
[2] Nash J.Equilibrium points in n-persons games[J]. Proc Nat Acad Sci, 1950, 36: 48-49.
[3] Simon H A.管理决策新科学[M]. 李柱流,等译.北京: 中国社会科学出版社, 1982.
[4] Selten R.Reexamination of the perfectness concept for equilibrium points in extensive games[J]. Inter J of Game Theory, 1975, 4: 25-55.
[5] Myerson R B.Refinements of the Nash equilibrium concept[J]. Inter J of Game Theory, 1978,7:73-80.
[6] Shapley L S.Equilibrium points in games with vector payoffs[J]. Naval Research Logistics Quarterly,1959,6:57-61.
[7] DING X P.Pareto Equilibria of MulTic-riteria Games Without Compactness, Continuity and Concavity[J]. Appiend Mathematics and Mechanics, 1996, 17(9): 847-854.
[8] YU J,YUAN XZ. The Study of Pareto Equilibria for Multiobjective Games by Fixed point and Ky Fan Minmax Inequality Methods[J]. Computers Math Applic,1998, 35(9): 17-24.
[9]YANGH,YUJ.EssentialComponentsofthesetofweaklyPareto-NashEquilibrumpoints[J].AppliedMathematicsLetters,2002,15:553-560.
[10] 汪波,杨辉. 双目标单群体博弈纳什均衡的存在性[J]. 西南民族大学学报(自然科学版), 2013, 39(6): 919-922.
[11]SandholmWH.PopulationGamesandEvolutionaryDynamics[M].London:MITPress, 2010: 21-51.
[12]胡毓达.多目标规划有效性理论[M].上海:上海科技技术出版社,1994:11-12.
[13]俞建.博弈论选讲[M].北京:科学出版社,2014:91-99.
(责任编辑:周晓南)
Existence of Weakly Pareto Perfect Equilibria for Multi-objective Population Games
CHEN Sha, YANG Hui*, YANG Guanghui
(College of Science, Guizhou University, Guiyang 550025, China)
Based on the refinement of equilibria under bounded rationality, the concept of weakly Pareto perfect equilibria for multiobjective population games was proposed. Firstly, the existence of weakly Pareto-Nash equilibria was proven by the application of ‘vector-valued Ky Fan inequality’. Moreover, the existence theorem for weakly Pareto perfect equilibria was established.
multi-objective population games; Ky Fan inequality; weakly Pareto-Nash equilibria; weakly Pareto perfect equilibria
1000-5269(2016)02-0010-04
10.15958/j.cnki.gdxbzrb.2016.02.03
2015-11-07
国家自然科学基金项目资助(11271098)
陈莎(1991-),女,在读硕士,研究方向:优化理论及应用,Email: chen_3623@163.com.
杨辉,Email:hui-yang@163.com.
O225
A
