海洋钻井过程中的井筒温度敏感性研究

孙万通　孟英峰　魏　纳　李永杰　李　皋　陈光凌

（油气藏地质及开发工程国家重点实验室·西南石油大学，四川　新都　610500）

海洋钻井过程中的井筒温度敏感性研究

孙万通孟英峰魏纳李永杰李皋陈光凌

（油气藏地质及开发工程国家重点实验室·西南石油大学，四川新都610500）

海洋钻井过程中，井筒中钻井液温度变化规律与常规陆地钻井不同，而由于钻井液流变性主要受井筒温度变化的影响，进而会影响到钻井施工的顺利进行。为此，需要深入了解海洋钻井井筒温度变化，以井筒能量守恒关系和传热学理论为基础，建立海洋钻井井筒温度分布数学模型，并采用数值模拟方法对其进行敏感性分析，形成海洋钻井井筒温度分布研究的数学方法，得到了其敏感性影响因素及变化规律：随排量增大，泥线以上井筒温度增大，泥线以下井筒温度降低；随注入温度增大，泥线以上井筒温度升高，泥线以下井筒温度保持不变；保温层使泥线以上井筒温度变化的幅度降低，有利于钻井液性能稳定。

海洋钻井井筒温度海水温度热交换敏感性

0　引言

海洋钻井过程中，由于海水的作用，泥线以上井段其钻井液温度会随着井深的增加而减小，而泥线以下井段由于地层的作用又随着井深的增加而增大，钻井液温度的这种变化规律与常规陆地钻井中随着井深增加而增大不同［1］。由于海底低温和地层高温的作用，钻井液性能会随井深的变化发生较大改变，进而影响井筒流动参数和钻井施工安全［2-5］。因此，深入研究海洋钻井井筒温度变化，对其影响因素进行敏感性分析，对于进一步分析钻井液流变性的全井筒剖面、海洋钻井安全施工等具有重大意义。为此，笔者在分析海水温度垂向分布的基础上，根据传热学理论和能量守恒基本定理，建立了海洋钻井井筒温度分布数学模型，然后采用数值模拟方法对其进行敏感性分析，形成了海洋钻井井筒温度分布研究的数学方法，得到了其敏感性因素及变化规律。

1　海洋钻井中井筒温度分布模型

1.1泥线以上井段

海洋钻井过程中，泥线以上井筒传热示意图如图1A所示。为得到海洋钻井井筒温度分布模型，假设钻井液在井筒中的流动为一维轴向流动，根据传热理论和能量守恒定律，建立传热微分单元体，如图2所示。环空中能量方程如下：

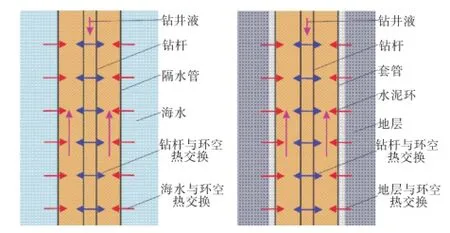
图1　井筒热量传递示意图

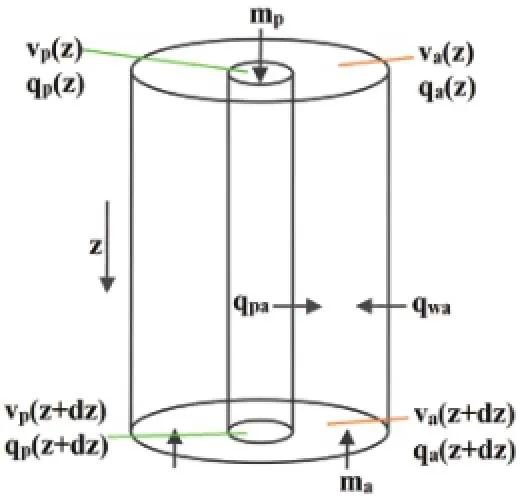
图2　井筒中传热微分单元体图

式中，ma为环空中流体质量流量，kg/s；va为环空流速，m/s；qa为环空中传热微分单元的焓变速率，J/s；g为重力加速度，m/s2；qwa为微元体上海水向环空的传热速率，J/s；qpa为微元体上钻杆向环空的传热速率，J/s；qfa为环空中微元体上钻井液摩擦产热速率，J/s。

式（2）中各参数求解过程如下：

环空中传热微分单元体的焓变速率为

其中

微元体上钻杆向环空的传热速率为

其中

微元体上钻井液摩擦产热速率［6-7］为

联合式（3）～（8）和式（2），整理得到

采用和环空温度分布相同的计算方法，可得钻杆内温度分布如下：

结合式（10）与式（12）可得钻杆内钻井液温度分布如下：

式中，mp为钻杆中流体质量流量，kg/s；vp为钻杆中流体流速，m/s；qp钻杆中传热微分单元体的焓变速率，J/s；qfp为钻杆中微元体上钻井液摩擦产热速率，J/s；pp为钻杆中的压力，Pa。

从式（10）和式（13）可以看出，无论是井筒中或者钻杆内，井筒温度的分布均与海水温度有很大影响，笔者对海水温度分布情况作如下分析：

海洋温度自上而下一般分为混合层、温跃层和恒温层。经过调研分析，根据我国南海实际情况，海水混合层垂向温度剖面为［8］：

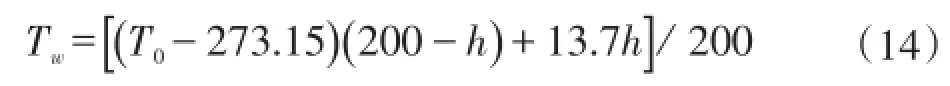
式中，T0为海表温度，℃；h为海水深度，m，0≤h≤200 m。

根据通用拟合公式，海水温跃层和恒温层的垂向温度剖面方程［9］：

式中，a1、a2、a3、a4为曲线拟合系数，a1=2.307 13，a2=39.398 39，a3=130.137 19，a4=402.731 77；h为海水深度，m，h≥200 m。

1.2泥线以下井段

海洋钻井过程中，泥线以下井筒传热示意图如图1B所示。对比泥线以上井筒传热示意图可以看出，泥线以下井段的井筒传热主要受到地层温度的影响，同理，可得环空中能量方程如下：

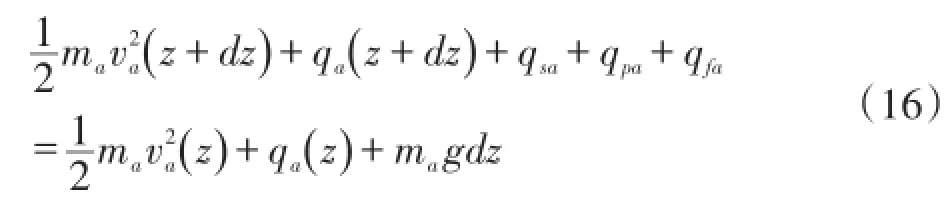
式中，qsa为微元体上地层向环空的传热速率，J/s；其他参数与泥线以上井段相同。

微元体上地层向井筒外壁的传热速率为

微元体上井筒外壁向井筒环空的传热速率为

其中

根据能量守恒，单位时间微元体上地层向井筒外壁的传热量等于单位时间微元体上井筒外壁向井筒环空的传热量，则可得微元体上地层向环空的传热速率为，采用与

泥线以上井段相同的方法，可得泥线以下井段环空内钻井液温度分布如下：

同理，泥线以下钻杆温度分布如下：

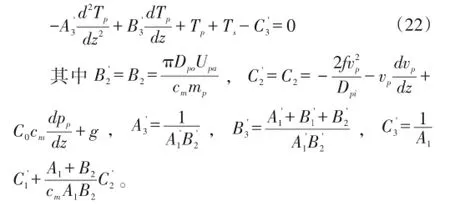
2数值求解

假设条件与边界条件如下：

1）钻井液循环时间足够长，井筒温度分布基本稳定。

2）钻杆中钻井液在井口的温度等于注入温度，即

3）钻杆中钻井液的井底温度等于环空中钻井液的井底温度，即

求解过程：海洋钻井井筒温度求解中，由于外界温度包括海水温度和地层温度两个不同计算过程的温度梯度，因此须采用数值方法进行求解。以井筒温度模型为基础，采用有限差分迭代方法［12］，对不同排量、不同注入温度、有无保温层条件下的井筒温度进行敏感性数值模拟研究。

3　算例分析

基础参数：正常钻进，井深4 500 m；海水深度1 500 m；隔水管直径508 mm；套管直径406 mm；套管下入泥线以下2 980 m；钻杆直径127 mm；钻头尺寸320.7 mm；地温梯度4℃/100 m。

3.1不同钻井液排量

假设海洋钻井过程中正常循环钻进条件下，循环时间足够长，海面温度和钻井液注入温度为25℃，井筒外无保温层，钻井液排量分别为30 L/s、50 L/s、70 L/s条件下，对井筒温度分布进行数值计算结果见图3。

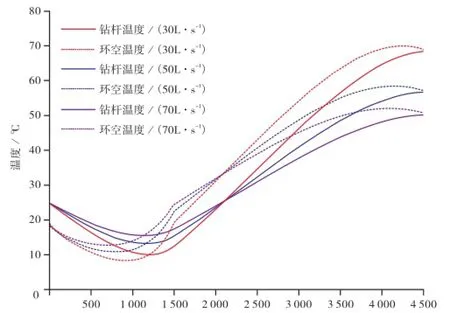
图3　不同排量下井筒温度分布图

从图3可以看出，排量从30 L/s增大到70 L/s，泥线以上海水井段，钻杆中的温度最小值从11℃增大到18℃，环空中的温度最小值从8℃增大到13℃；泥线以下井段，随着排量增大，钻杆和环空中的温度均有所降低，井底温度从69℃降低到50℃。主要原因是随着钻井液排量的增大，井筒中的流体与海水、地层换热不充分。在泥线以上井段，海水温度随着井深变大而降低，因此排量增大会造成井筒温度变大；在泥线以下井段，地层温度随着井深变大而升高，因此排量增大会造成井筒温度变小。

因此，海洋钻井过程中，为了避免产生较大的温度波动，进而造成钻井液流变性的变化和井筒施工参数的改变，可以适当增大钻井液排量。

3.2不同钻井液入口温度

假设海洋钻井过程中正常循环钻进条件下，循环时间足够长，钻井液排量为50 L/s，钻井液注入温度分别为20℃、25℃、30℃，井筒外无保温层条件下，对井筒温度分布进行数值计算结果见图4。

图4　不同注入温度下井筒温度分布图

从图4可以看出，钻井液注入温度从20℃增大到30℃，泥线以上海水井段，钻杆中的温度最小值从13℃增大到17℃，环空中的温度最小值从10℃增大到14℃，环空井口温度从16℃增大到21℃；泥线以下井段，钻杆和环空中的温度随注入温度的增大变化不大，井底处的温度均维持在58℃左右。主要原因是钻井液入口温度较大，泥线以上井段，注入钻井液与海水换热时间较短，其温度仍然较高；而泥线以下井段，地层温度相同，由于井筒中的钻井液与地层接触时间较长而换热充分，其最终到达井底处的温度主要受地层温度的影响，因此，泥线以下井段，钻杆和环空温度随着注入温度的增大变化不大。

因此，海洋钻井过程中，为了避免钻井液流变性由于井筒温度变化而发生较大变化，应根据环境条件适当调整钻井液入口温度以稳定钻井液性能。

3.3保温层的影响

海洋钻井中，隔水管外层安装保温层对稳定井筒温度具有有利作用。为了深入了解保温层对海洋钻井井筒温度的影响，笔者假设正常循环钻进条件下，循环时间足够长，海面温度和井筒注入温度为25℃，排量为50 L/s，井筒外是否有保温层条件下，对井筒温度分布进行数值计算结果见图5。

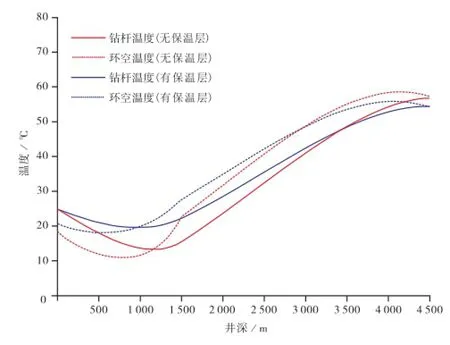
图5　有、无保温层时井筒温度分布图

从图5可以看出，海洋钻井过程中，井筒外有无保温层，对泥线以上井段井筒温度变化影响较大。图5中，有保温层时，钻杆中最低温度为21℃，环空中最低温度为18℃；无保温层时，钻杆中最低温度为14℃，环空中最低温度为11℃。主要原因是保温层的加入使井筒与海水的换热系数降低，泥线以上井筒温度变化较小，最低温度高于无保温层条件下的井筒最低温度。

因此，海洋钻井过程中，在海水井段加入保温材料可以防止井筒温度大幅变化，进而稳定钻井液性能。

4　结论

1）分析了海洋钻井中井筒与海水、地层的传热机理，建立并推导了海洋钻井井筒温度数学模型，并以此对海洋钻井井筒温度进行数值分析，得到了其敏感性影响因素，为钻井液流变性的全井筒剖面分析和海洋钻井安全施工设计奠定了重要基础。

2）通过分析得到：随排量增大，泥线以上井段井筒温度升高，泥线以下井段井筒温度降低，适当增大排量有利于钻井液性能稳定；随注入温度增大，泥线以上井段井筒温度升高，泥线以下井段井筒温度保持不变，合理调节入口温度有利于控制钻井液流变性；保温层可促进泥线以上井段井筒温度变化幅度降低，有利于钻井液性能稳定和海洋钻井安全施工。

［1］管志川.温度和压力对深水钻井油基钻井液液柱压力的影响［J］.石油大学学报：自然科学版，2003，27（4）：48-52.

［2］霍宝玉，闫志怡，张晓崴，等.海洋深水水基钻井液低温流变实验和配方优选［J］.东北石油大学学报，2013，37（6）：94-100.

［3］王友华，吴彬，徐绍成.水基钻井液体系在低温条件下的流变性探讨［J］.石油天然气学报，2005，27（4）：106-107.

［4］张玉婵，刘平安，唐馨，等.海洋深水钻井钻井液研究进展［J］.中国科技博览，2014（27）：101.

［5］潘一，刘天龙，杨双春.国内外海洋钻井液研究现状［J］.油田化学，2015（2）：292-295.

［6］Xiaodan Zhao，Jiuping Xu.Numerical simulation of temperature and pressure distribution in producing gas well ［J］.World Journal of Modelling and Simulation，2008，4 （2）：94-103.

［7］Thompson M，Burgess T M.The prediction of interpretationofdownholemudtemperaturewhiledrilling［J］. SPE14180，1985.

［8］Wang Z M，Hao，X N，Wang X Q，et al.Numerical simulation on deepwater drilling wellbore temperature and pressure distribution［J］.Petroleum Science and Technology，2010，28（9）：911-919.

［9］刘国祥，令文学，黄家华，等.海洋钻井井筒内温度确定［J］.海洋石油，2008，28（4）：83-86.

［10］Hasan A R.Heat transfer during two-phase flow in wellbore，part I formation temperature［C］.SPE Annual TechnicalConferenceandExhibition，Dallas，Texas，1991.

［11］郭春秋，李颖川.气井压力温度预测综合数值模拟［J］.石油学报，2001，22（3）：100-104.

［12］任敏.井筒—地层温度压力耦合场模拟研究［D］.武汉：中国地质大学，2014.

（编辑：李臻）

B

2095-1132（2016）04-0036-05

10.3969/j.issn.2095-1132.2016.04.010

修订回稿日期：2016-07-05

中国工程院—国家自然基金委联合咨询项目（L13220021）、国家自然科学基金青年基金项目（NO.51204140）资助。

孙万通（1992-），博士研究生，研究方向为油气井工程。E-mail：1403543721@qq.com。