基于模糊PD控制器的桥式起重机防摇与定位研究

王照萌+陆永耕+袁昕天+刘梦花

摘 要：消除并控制吊重的摇摆对提高起重机工作效率、减少装卸作业安全生产隐患具有重要意义。考虑到吊重摇摆系统的非线性、时变性和不确定性，提出了一种将传统PD控制与模糊控制相结合的方法，利用模糊语言规则对PD参数进行实时整定。利用SIMULINK对防摇摆系统进行了建模和动态仿真研究，通过对仿真结果分析，在给定钢丝绳绳长、载重质量前提下，相对于传统PD控制方法，该控制方法具有更好的适应性和鲁棒性，可以提高起重机摇摆系统的动态性能。

关键词：模糊PD控制器；桥式起重机；模糊控制；鲁棒性

中图分类号：TH215 文献标识码：A DOI：10.15913/j.cnki.kjycx.2016.15.007

桥式起重机被广泛应用于码头、仓库、水电站等各个领域。在起重机作业的过程中，由于惯性的存在，重物及钢绳会在小车启动、运行和制动过程中绕悬吊点产生摆动，不仅会影响生产效率，还会增加作业时间，影响起重机的稳定性，严重时，甚至会引起安全事故。许多学者在这方面进行了大量的研究，比较有代表性的研究有LQR最优控制、PD和PID控制、自适应控制、状态反馈控制等。这些控制方法都是基于对被控制对象建立的精确数学模型设计的，虽然容易实现，但缺乏应变性和灵活性，控制效果不理想，而且起重机在实际运行过程中要考虑到小车与轨道间的物理摩擦和风力等外界干扰以及自身的非线性因素的影响，模型很难达到现实要求，在防摇摆系统的应用中也会有一定的局限性。

本文基于模糊控制的设计思想，同时结合传统的PID控制原理，将起重机PD控制与模糊控制相结合构建自适应PD控制器，从而实现控制参数的最佳调整，进一步增强系统对不确定因素的适应性。仿真结果表明，自适应模糊PD控制超调量小、震荡小，提高了起重机在运行过程中的控制精度。

1 起重机吊载系统模型

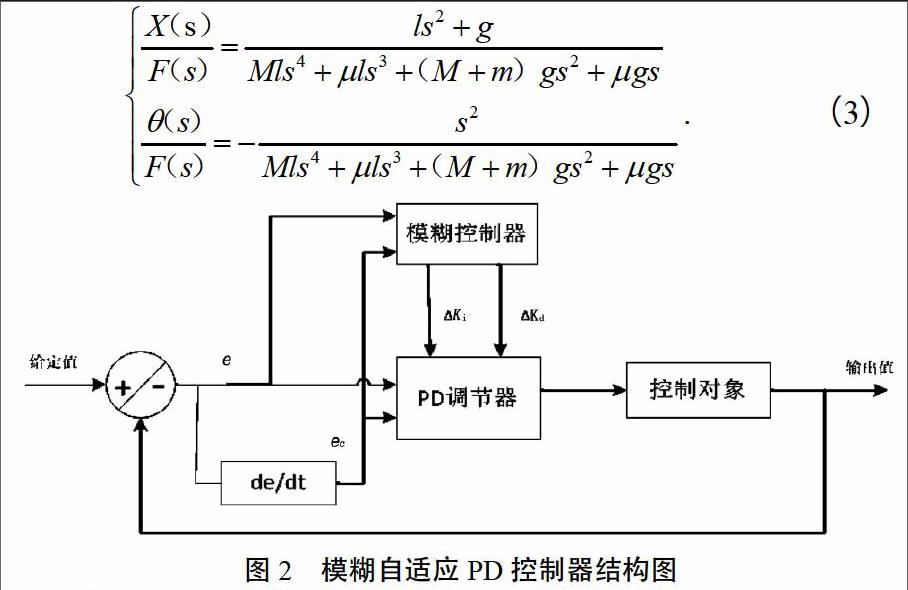
桥式起重机整个控制系统包括对大车、小车位置与吊载摆动角度的控制，且二者都相互近似独立。对起重机系统建模，如图1所示，其中，小车质量设定为M，吊载质量为m，电机驱动力为F，小车受到的摩擦力为f，小车启动后沿X轴方向运动，由于惯性作用吊载会产生摆角θ。

2 模糊PD控制器的结构

2.1 模糊PD控制器结构原理

模糊PD控制器由一个常规PD控制器和一个模糊控制器组成。选用二维模糊控制器，输入变量信号其一为小车位移偏差信号e，其二为小车位移偏差变化信号ec，输出变量信号ΔKp、ΔKd分别是常规PD控制器的两个增量参数。采用这种增量型模式来整定参数是为了满足不同的e和ec对控制器参数的不同要求，控制器会在系统运行中始终检测信号e和ec，基于设定的模糊逻辑规则对两个增量参数在线修整，其控制结构如图2所示。

2.2 模糊控制规则的设定

与传统PID控制器类似，模糊自适应PD控制参数的整定也遵循一定的原则，ΔKp、ΔKd各参数在控制系统中分别起着不同的作用，并与e和ec之间也有着一定的关系。

控制ΔKp这个参数是为了加快系统的响应速度，进而提高系统的调节精度，而控制ΔKd的作用在于提前判断系统偏差的变化方向，当变化到来时，提前作出制动，及时抑制偏差的产生。换句话说，通过调整ΔKd的大小来改善系统的动态特性。

当偏差e较大时，为保证系统良好的跟踪性能，提高系统的响应速度，ΔKp应取大值，ΔKd取小些。当偏差e较小时，为避免超调过大而出现振荡的情况，应适当减小ΔKp的值，同时，综合考虑系统的抗扰动能力和系统响应速度，应使ΔKd适当取值。但ΔKd不能过大。因为过大会使响应过程过分提前制动，从而延长调节时间。当e和ec同号时，输出的方向会朝着偏离稳定值的趋势变化。此时，ΔKp应适当增大；反之减小。

2.3 隶属度函数

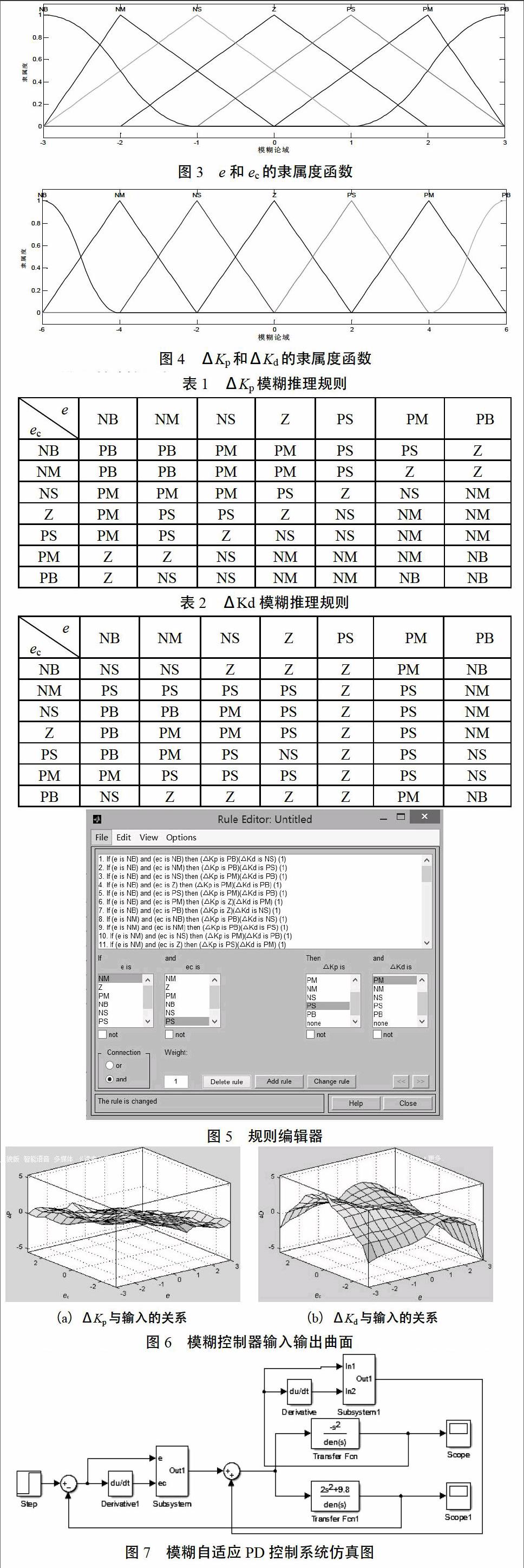
将输入、输出变量的模糊语言取为“NB（负大），NM（负中），NS（负小），Z（零），PS（正小），正中（PM），正大（PB）”，输入信号e和ec的基本论域分别是[-1，1]和[-0.4，0.4]，量化因子分别取3.0和7.5，输出信号ΔKp、ΔKd的基本论域分别是[-8，8]和[-10，10]，输入输出信号分别映射至模糊论域[-3，3]和[-6，6]，且采用三角形函数作为隶属函数曲线，如图3和图4所示。

2.4 模糊控制规则

基于过程控制相关知识以及专家长期积累的经验得出模糊控制规则，通过观察控制系统的响应曲线，结合曲线动态性能指标的分析，不断对控制规则进行修整，多次调试后，最后确定的模糊控制规则具体见表1和表2.

以误差和误差变化为输入量的二维模糊控制器，由表1和表2的控制规则，结合二维模糊控制器自身的条件语句，将输入、输出的模糊逻辑控制量安排到规则编辑器中，如图5所示。

用三维曲面分别表示输入e，ec与输出ΔKp、ΔKd的逻辑关系，如图6所示。

从图6中可以看出，当ΔKp在e和ec较大时，取大值；当ΔKd在 较小时，取值大；e和ec不同号时，ΔKp值相比同号时较小。

2.5 输出量的反模糊化

控制量需要通过比例因子变换到基本论域上，即由模糊控制语言转化为精确数学语言来获得控制参数的真实分布，也就是输出量的反模糊化，根据重心元素的求取公式，在线求得ΔKp、ΔKd值乘以各自参数的比例因子，与设定的初始参数Kp0，Kd0求和，其结果作为模糊自适应PD控制器输出值，即控制器实时参数整定值。

式（4）中：Kp0，Kd0为PD控制两个参数的初始值；ΔKp和ΔKd为两个参数的修正值；Kp，Kd为PD控制两个参数的取值。

3 控制系统的仿真与实验验证

3.1 起重机模糊自适应PD防摇摆控制系统

在MatLAB/Simulink软件平台上建立防摇系统模型，如图7所示。该系统的控制策略主要包含通过对两个模糊PD控制器的设计来实现小车位移和吊载摆角的控制，控制过程分别以小车位移和吊载摆角为两个控制器的反馈信号。其中，位移反馈信号与输入参考信号构成位移偏差信号，经整定的吊载摆角信号则以正反馈的形式接入控制系统中。

参数的在线整定是基于模糊语言规则来完成的。这种根据系统实时状态来实时控制的方法使被控对象具有良好的动、静态性能。

3.2 仿真实验

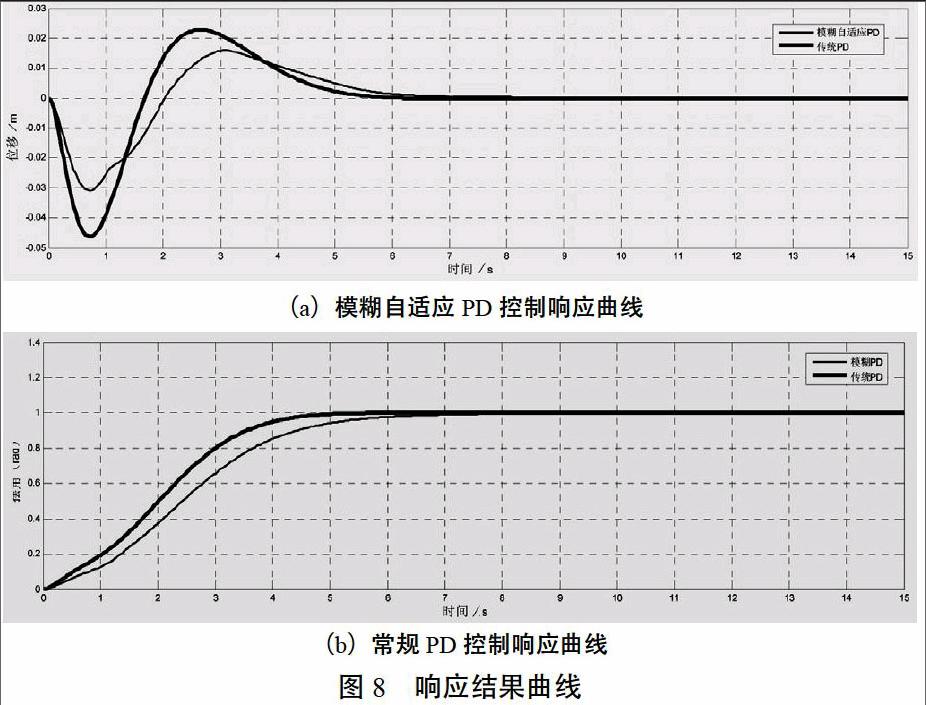
为了验证控制系统的性能，选取1组起重机参数来进行MatLAB仿真测试。假定参数：小车质量M=5 kg，吊重质量m=10 kg，吊绳长度L=2 m，重力加速度g=9.8 m/s2，目标位置和期望摆角分别以单位阶跃输入1 m和0°为参考量，采样时间选定15 s。响应结果曲线如图8所示。

分析仿真结果可知，与常规PD控制相比，模糊自适应PD控制算法明显降低了载荷的摇摆幅度，超调量也更小。相比起来，模糊自适应PD控制算法具有较强的鲁棒性。

4 结束语

本文采用模糊语言规则根据系统的运动状态来实时地自动整定PD的控制参数，对起重机运行过程进行了仿真。为了更好地分析出控制系统的优劣性，先通过改变可调参数（钢丝绳长和吊载质量）的数值大小设计出了多组对比试验，然后引入了外界干扰信号，从响应结果曲线和动态性能指标的角度上实现了模糊自适应PD控制算法和常规PD控制算法的分析和对比。结果验证了模糊自适应PD控制器比常规PD控制器具有较强的鲁棒性。

参考文献

[1]李伟，吕景惠.起重机线性二次型最优消摆控制[J].电气传动，2003（02）：21-24.

[2]P. Pivoňka.Physical Background of Fuzzy PI and PDController.IFSA 8th International Fuzzy Systems Association World Congress.Taipei：1999.

[3]刘金琨.先进PID控制及其MATLAB仿真[M].第3版.北京：电子工业出版社，2011：174-178.

[4]黄凯.起重机自适应智能防摆控制方法及其仿真研究[D].南京：南京林业大学，2007.

[5]钟斌，程文明，吴晓，等.桥门式起重机吊重防摇状态反馈控制系统设计[J].电机与控制学报，2007，11（5）：492-496.

[6]D.Liu.Adaptive sliding mode fuzzy control for a two-dimensional overhead crane.Mechatronics，2005（15）：505-522.

[7]Benhidjeb A，Gissinger G L.Fuzzy control of Overhead Crane Performance Comparisons with Classic Control. Control Engineering Practice，1995，3（12）：1687-1696.

〔编辑：刘晓芳〕