高中几何概型教学策略探讨
2016-09-22刘姗张清芳
刘姗++张清芳
【摘 要】 几何概型是高中数学课程的新增内容,也是一个重要的概率模型,对于概率的学习有着非常重要的意义,高中生在学习这部分内容时存在诸多困难。对此,文章提出了相应的教学策略,以帮助高中生更好地理解并掌握几何概型知识。
【关 键 词】 几何概型;高中数学;教学策略
中图分类号:G633.6 文献标识码:A 文章编号:1671-0568(2016)24-0060-03
几何概型,是指如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称几何概型。几何概型是高中数学课程改革中的新增内容,也是一个重要的概率模型。相比中学数学中的其它概念,“几何概型”的概念是比较抽象的,学生在学习这部分内容时往往存在诸多困难,遇到具体问题时常出错,且不易找到错误原因。为此,笔者特提出如下几点教学应对策略:
一、加强对几何概型知识的理解
在几何概型的学习中,深刻理解几何概型知识主要体现为对几何概型核心思想(等可能性与无限性)的掌握。学生只要掌握了几何概型的核心思想,就能够突破古典概型的干扰,分辨出几何概型,从而对几何概型做出自己的解释与判断,形成自己的见解,进而通过自己对几何概型的理解,来解决有一定难度的几何概型问题。为此,在教学中,教师应做到以下几点:
1. 对比两大概率模型,弄清本质区别
几何概型与古典概型既有联系又有区别,根据这一特点,教师在教学中一定要重视概率中几何概型和古典概型的对比,要弄清两者的区别,让学生学会区分这两大概型。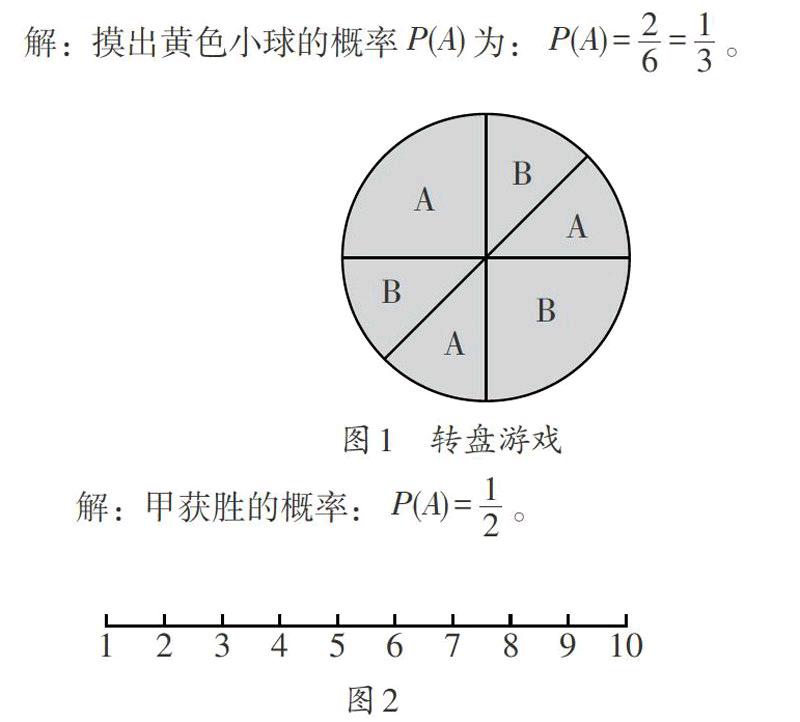
例1 一个黑色的袋子里装有6个大小完全相同的小球,其中有3个黑色小球,2个黄色小球,1个红色小球,问:在摸取一次的情况下,摸出是黄色小球的概率是多少?
解题思路分析:问题给定的是6个小球,在只摸取一次的情况下,一共会出现6种可能结果,即基本事件个数满足有限性;并且摸出任何一个小球的机会是相等的,即满足基本事件是等可能的,由此可以判断出该题是一道古典概型的问题。
解:摸出黄色小球的概率[P(A)]为:[P(A)=26=13]。
例2 转盘游戏,图中有两个转盘,甲乙两人玩转盘游戏,规定当指针指向A区域时,甲获胜,否则乙获胜,求甲获胜的概率。
解题思路分析:从这个图表(图1)中可以看出A与B分别是整个圆的一半,即在转盘游戏中,甲或乙获胜的概率各是[12],因此,满足几何概型基本事件的等可能性。又由于指针落在某一个区域的任何一个点都是有可能的,即基本事件有无限多个,因此可以判断该题满足几何概型的条件,即求甲获胜的概率只与A区所占的面积与整个圆的面积比有关。
解:甲获胜的概率:[P(A)=12]。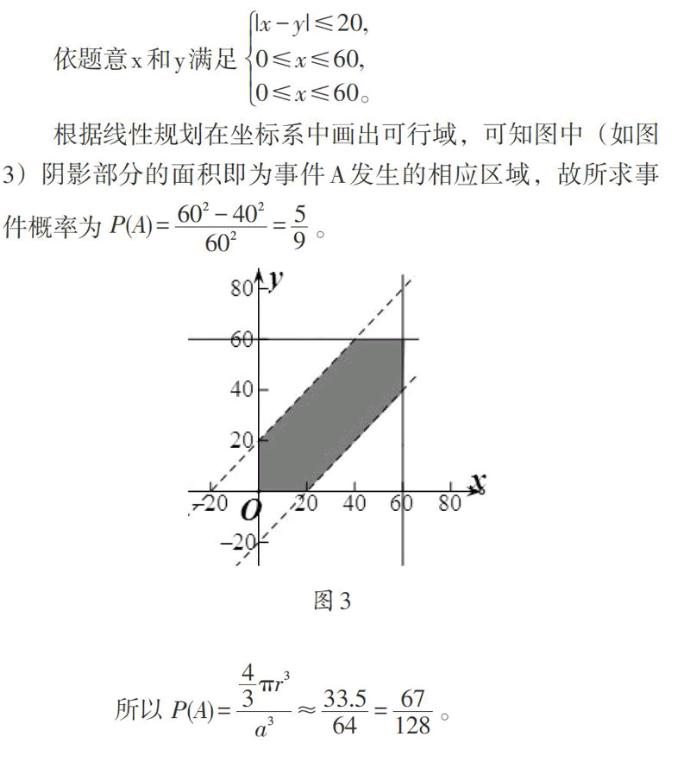
以上两题是典型的古典概型和几何概型的问题,学生解答时常常容易混淆。因此,教师在讲解时,应重点指出几何概型与古典概型的区别,还要将两大概型的定义、特征以及计算公式对学生讲清、讲透,让学生弄清它们的本质区别。
2. 借助多媒体演示,增强对几何概型的理解
由于几何概型知识具有抽象性的特点,学生学起来存在一定的困难。针对这一问题,笔者认为,教师在教学中不妨借助实验演示,引导学生观察蕴含在具体问题中的几何概型特点,从而增进对几何概型知识的理解。
例3 边长为4厘米的正方形及其内部有一圆,若随机向正方形内扔一粒豆子,则豆子落在圆和正方形夹部分的概率是多少?
对于这个问题如何求解,多数学生都会感到很茫然,不知从哪里入手。教学时,教师不妨借助多媒体课件,将在正方形内扔豆子这一过程制作成动画图片,引导学生观察随着圆的大小的改变,豆子的运动轨迹,继而求出概率。通过多媒体演示,学生直观感受到从圆的变动到轨迹的形成过程,进而加深对几何概型的理解。此外,通过多媒体动画演示,还可以营造出良好的学习氛围,促使学生积极参与课堂教学,最终提升教学效率。
3. 结合生活经验,让学生感知几何概型
在几何概型的学习中,应注意结合学生的生活经验,让学生自己感知几何概型,建构对几何概型的理解,这是对几何概型知识加深理解的有效策略。比如,在讲授几何概型问题时,可以设置基本事件的个数由有限到无限的、由简单到复杂的问题情境,让学生在自己的认知冲突中发掘几何概型的本质特征,只有这样,学生习得的知识才会牢固,对几何概型的理解也才会更加深刻。
二、注重模型的建构和转化
建构几何概型的首要任务是计算事件A包括的基本事件对应的区域的长度、面积或体积,但这里的计算并非重点,重点在于如何利用几何模型,把问题转化为各种几何概型问题。为此,可参考以下办法:适当选择观察角度;把基本事件转化为与之对应的区域;把随机事件A转化为与之对应的区域;如果事件A的对应区域不好处理,则可以用对应事件概率公式进行逆向思考。在此基础上,再从长度、面积和体积分类考虑具体模型的建立。
1. 与长度有关的几何概型
这类问题通常是在一维空间中出现,即题目中涉及一个变量,可以近似地抽象为一条线段,该问题求解的事件A的概率就转化成求满足所求事件的线段长,从而将抽象、复杂的问题简单化。
例4 若A=[1,10],则从A中任意取出一个数,求出这个数不大于4的概率是多少?
解答思路分析:在1至10中任意取一个数是一个基本事件,基本事件有无数个,且每一个基本事件的发生都是等可能的,因此,事件发生的概率只与长度有关,符合几何概型条件。endprint
解:记B为“在1至10中任意取一个不大于4的数”,画出从1到10的线段长(如图2),将线段分为9段长,而不大于4的线段长为3段,所以[P(B)=39=13]。
一般说来,将每个事件理解为从某个特定的几何区域内随机地取一点,该区域中每一点被取到的机会都一样,而一个随机事件的发生则理解为恰好取到上述区域内某个指定区域中的点,这样的概率模型就可以用几何概型求解。
2. 与面积有关的几何概型
当概率问题中涉及两个变量,则此问题可以利用平面直角坐标系来讨论,从而将实际问题转化为求面积之比,建立起概率模型。
例5 两人相约8点到9点在某地见面,先到者等候后到者20分钟,过时就可离开,求这两人能会面的概率是多少?
解题思路分析:此问题中的“两人在8点到9点之间的任何一个时间到达某地”是一个基本事件。显然,这里的基本事件有无数个,且基本事件发生都是等可能的。同时考虑到两个人能见面,有两个变量,因此,事件发生的概率只与面积有关,符合几何概型的条件。
解:记事件A为“两人在8点到9点之间能见到面”,分别设出两人到达时间为x和y,
依题意x和y满足[|x-y|≤20,0≤x≤60,0≤x≤60。]
根据线性规划在坐标系中画出可行域,可知图中(如图3)阴影部分的面积即为事件A发生的相应区域,故所求事件概率为[P(A)=602-402602=59]。
在解答这类问题时要根据题意找出条件,依据线性规划在坐标系中画出可行域,并求出事件A发生的相应区域。解答这类问题的关键就是建立起关于面积的概率模型。
3. 与体积有关的几何概型
当几何概型问题中涉及3个变量,或是在三维空间中进行的概率计算,可转化为体积计算。
例6 在棱长为4的正方体内有一内切球,若在正方体内任取一点,求该点在球内的概率。
解题思路分析:此题中“在正方体内切球内任取一点”是一个基本事件,基本事件也有无数个,且基本事件发生都是等可能。由此可结合正方体图形的特点,引入3个空间变量。故此,事件发生的概率与体积有关,符合几何概型条件。
解:记A为“在正方体内任取一点在内切球中”,分别求出正方体与球的体积,
所以[P(A)=43πr3a3≈33.564=67128]。
此题的结果显然与正方体和球的体积有关,只要分别求出正方体与球的体积问题就解决了。在这类问题中,关键是找到变量个数,以便建立体积模型。
三、加强思维训练
1. 暴露思维过程,把握思维脉络
我们知道,教学并不是单向地传输知识的过程,而是对知识的一个加工、转化和处理的过程。几何概型是古典概型的拓展与延伸,其学习过程蕴涵着重要的思维过程。因此,教师在教学过程中应注意以下两点:首先,在讲授几何概型知识时,应将学生原有的古典概型知识经验作为几何概型知识新的生长点,使学生对已有的古典概型知识经验进行重新改造、加工、扩展,从而更好地理解并丰富几何概型新知识。其次,教师在教学过程中不仅要注意展示问题发生、发展的思维方式,还应听取学生的想法,注意创造机会,让学生在自主、合作与探究学习的过程中,将自己对几何概型问题的认识、思考和分析的思维过程暴露出来,以利于教师准确地把握学生的思维脉络,掌握学生在解决几何概型问题的困难所在,从而有针对性地进行教学。比如,对于一道几何概型题的讲解,我们应关注如下问题:学生是如何读题的,又是如何思考的?解答中有什么困惑?等等,其目的就是让学生的思维得以充分暴露,使教师能够掌握学生的思维动态,从而使几何概型教学更具针对性和有效性。
2. 多角度举例,培养思维的深刻性
高中生在刚刚接触几何概型的时候,对新知识存在理解上的困难,学生无法准确掌握几何概型与古典概型的本质区别,没有养成几何概型的概率思维。因此,教师在教学中应当进行多角度举例,让学生全方位感受几何概型的特点,从而理解新知识。在举例方面,教师既要运用正例,也要选用合适的反例:正例有利于学生巩固几何概型知识,反例则能强化或深化学生对几何概型知识的本质理解。实践证明,合理、恰当地运用正反例,不仅能有效引导学生的思维,有助于几何概型知识的学习和掌握,而且还能培养学生思维的深刻性。
3. 变式教学,培养思维的灵活性
在几何概型的教学过程中,我们经常会听到老师们抱怨:“这个问题明明讲过,学生也做过,考试时只是稍微变了一下形式而已,他们就不会做了!”这说明学生并未真正理解问题,变通能力不强。变式教学可以为解决这个问题提供方法和途径,比如,改变几何概型问题的条件或结论,将条件的范围扩大或者缩小,等等,通过对此类问题的改变,学生在解题时就可以举一反三、触类旁通。
参考文献:
[1] 郭凤艳.浅谈数形结合思想及在概率中的应用[J].高教论坛,2015,(11):19.
[2] 孙丹丹.几何概型的构建[J].数理化解题研究,2014,(4):14.
[3] 程海奎,陈雪梅.是强调几何度量还是关注模型的建构[J].数学通报,2014,(11):26.
(编辑:朱泽玲)endprint
