利用α-F环分析Blazar 3C454.3的长周期光变

袁聿海，张心瑜，郭宁莉，张冠军

（广州大学　物理与电子工程学院，广东　广州 510006）

利用α-F环分析Blazar 3C454.3的长周期光变

袁聿海，张心瑜，郭宁莉，张冠军

（广州大学物理与电子工程学院，广东广州 510006）

通过研究辐射谱和流量密度之间的关系，可以分析与辐射有关的辐射过程以及其中蕴含的辐射理论.文章利用UMRAO（美国密歇根大学射电天文台）数据库，从中挑选了1个具有比较多观测数据的源——3C454.3.利用该源的流量密度（F），计算了对应的谱指数（α），得到α的范围为-0.339±0.038至0.517± 0.013，平均值为=0.171±0.217.流量密度和谱指数之间存在比较强的反相关：α=（-0.057±0.004）F14.5+ 0.758±0.039，相互系数为r=-0.778，差异概率P＜0.01.在流量密度和谱指数的分布中存在着2个比较明显的椭圆环结构，其时间跨度分别为5.82 a和6.71 a，该时间跨度与源的长周期光变时标是一致的.

Blazar星系；个别；3C454.3；谱指数

Blazars星系是具有快速光变、高且变化的偏振、强射电辐射和视超光速运动等特殊性质的一类活动星系.该星系包括FSRQs和BL Lac 2类.它们从射电到X射线甚至γ射线都被发现具有光变性质，并且光变的时标可以从小时到年的量级［1-2］.Blazars不同时标的光变可以通过吸积盘的不稳定性、星系内部的超大黑洞，以及相对论喷流效应等物理模型加以解释.

相对论喷流效应可以解释许多极端的观测性质［3］，因而Blazars是研究极端相对论喷流的最佳实验室.很多学者都在Blazars中发现了环状的时间间隔，比如AO 0235+164，1308+326，2223-052等，该环状结构很可能与Blazars的长准周期有 关［4-6］.

3C454.3（PKS2251+158，OY091）是一个比较亮的、变化比较剧烈的活动星系，并且在光学和射电波段存在着比较明显的相关性［6］.为了计算该源的光变周期，WEBB等［7］利用1971～1985年的B波段的观测数据得到该源具有0.8 a、3.0 a和6.4 a长周期光变.CIARAMELLA［8］利用UMRAO数据得到6.3±0.2 a的长周期光变.KUDRYAVTSEVA等［9］利用UMRAO数据和MetsÄahovi射电数据得到该源具有6.2±0.1 a和12.4±0.2 a等2个长周期光变.FAN等［10］利用UMRAO数据分析得出该源具有6.2±0.2 a和12.3±1.8 a的光变周期.

1　样 本

本文选取的射电流量来自美国的UMRAO数据，对应的频率分别为4.8 GHz，8.0 GHz和14.5 GHz.利用以下方法来计算它们的平均流量密度和谱指数：①将每个波段的每隔7 d的流量密度取平均数（4.8 GHz，8.0 GHz和14.5 GHz），这样得到了N组流量密度，每组流量密度在3个波段的流量 密度 分别是 F4.8 GHz，F8 GHz和F14.5 GHz；②利用关系式Fv∝v-α（v=4.8 GHz，8.0 GHz，14.5 GHz）得到对应的谱指数.

对于3C454.3，计算后得到162个谱指数（α），其变化范围从-0.339±0.038至0.517± 0.013，平均值为¯α=0.171±0.217.谱指数和平均流量密度见图1，其中，上图代表平均光变曲线，下图代表谱指数.

图1　3C454.3的平均光变曲线和谱指数Fig.1 The averaged lightcurve and spectral index of 3C454.3

2　谱指数与流量密度的关系

2.1数据分析方法

对2个变量x和y，一般可以可用线性拟合的方法来分析2者之间的相关性，y=（k±Δk）x+ （k0±Δk0），相关系数为r，差异水平为 P，这里k和Δk分别是斜率以及对应的误差，k0和Δk0分别是截距及其误差.但当2变量之间不是线性的分布，而是椭圆结构分布时，则相应椭圆结构可以利用如下椭圆曲线进行拟合：

这里a，b，c，d，e，f是自由参数，|a|代表被归一化.

2.2分析结果

利用上式分析3C454.3中谱指数α和射电流量密度F14.5之间的关系，得到如下结果：α= （-0.057±0.004）F14.5+0.758±0.039，相关系数为 r=-0.778，差异水平 P＜0.01，见图2.

图2　流量密度和谱指数之间的相关性Fig.2 The correlation between the flux density and spectral index

α和F14.5的分布在JD2 444 403.374至JD2 446 530.701，构成了椭圆环1结构，该椭圆环的时间跨度为2 127 d（5.82 a），沿着时间的顺序，椭圆环的变化方向是逆时针方向，见图3（实心点）.同样，从JD2 446 665.766至JD2 448 920.314，α和F14.5构成椭圆环2，该椭圆环的时间跨度为2 254 d （6.17 a），见图3（空心点）.

利用椭圆曲线进行拟合，得到如下结果：对于椭圆环1，拟合曲线为-0.003x2-0.058xy-0.458 4y2+ 0.075 4x+0.756 4y-0.456 8=0，在图3中用实线表示；对于椭圆环2，拟合曲线为-0.002 5x2-0.058 3xy-0.589 3y2+0.057 8x+0.737 1y-0.320 3=0，在图3中用虚线表示.

图3　α和F14.5Fig.3 Using the elliptic curve to fitting the relation between a and F14.5

3　讨 论

在许多论文中都曾经涉及到Blazars的谱指数与流量密度之间的关系.STEVENS等［11］分析过αro和αrx（r，o，x分别表示无线电波段，光波段和X射线波段）的分布，并且得到这2个谱指数是相关的.TREVESE等［12］得到谱指数的变化幅度与流量密度的对数是呈线性相关的.

如果基于椭圆环的时间跨度，对该源的光变曲线进行分割，可以得到图4所示的结果.这2个椭圆环的可变范围是与光度曲线的可变范围相一致的，由此可以得出这2个椭圆环的时间跨度很可能与长准周期的光变时标相一致.

FAN等［10］分析了该源在射电波段的长周期光变.结果如下：在4.8 GHz，存在6.2±0.2 a和12.3±1.8 a的光变周期，在8 GHz存在6.7±0.1 a和13.6±1.1 a的光变周期，在14.5 GHz存在6.3±0.2 a的光变周期.本文通过研究该源在14.5 GHz的谱指数与流量密度的分布，发现椭圆环结构，得到相应的时间跨度分别为5.82 a和 6.17 a.由此可见，该时间跨度与FAN等［10］得到的光变周期是一致的.

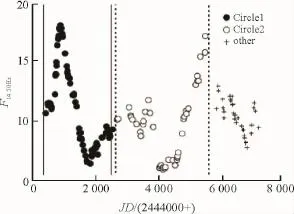
图4　在14.5 GHz波段，平均光度曲线随时间的变化Fig.4 The variability of averaged lightcures at 14.5 GHz

许多学者利用相对论喷流在螺旋磁场中的运动激波模型来解释流量的变化幅度［13-16］.本文的结果可以解释螺旋场的旋转周期与流量密度之间的关系，射电波段的长周期光变很可能来自喷流和螺旋磁场.

本文中，基于多波段的光变曲线，计算了3C454.3的射电谱指数，该谱指数的变化范围从-0.339±0.038至0.517±0.013，谱指数的平均值为¯α=0.171±0.217.在流量密度和谱指数的分布中存在着2个比较明显的椭圆环结构，其时间跨度分别为5.82 a和6.71 a，并且该时间跨度与该源的长周期光变时标是一致的.

感谢：本研究所利用的数据来自密歇根射电天文观测台并受到密歇根大学和美国国家科学基金会的支持.

［1］ ULRICH M H，MARASCHI L，URRY C M.Variability of active galactic nuclei［J］.ARA&A，1997，35：445-502.

［2］ FAN J H.Optical variability of Blazars［J］.ChJAS，2005，5：213-223.

［3］ URRY C M，PADOVANI P.Unified schemes for radio-loud active galactic nuclei［J］.PASP，1995，107，803，845.

［4］ KIDGER M R.The 11 year period in OJ 287 revisited：Is it a true long-enduring period［J］.AJ，2000，119（5）：2053-2059

［5］ PURSIMO T，TAKALO L O，SILLANPAA A，et al.Intensive monitoring of OJ 287［J］.A&AS，2000，146（1）：141-155.

［6］ PYATUNINA T B，KUDRYAVTSEVA N A，GABUZDA D C，et al.Frequency-dependent time delays for strong outbursts in selected Blazars from the Metsähovi and UMRAO monitoring data bases-Ⅱ［J］.MNRAS，2007，381（2）：797-808.

［7］ WEBB J R，SMITH A G，LEACOCK R J，et al.Optical observations of 22 violently variable extragalactic sources 1968-1986［J］.AJ，1988，95（2）：374-397.

［8］ CIARAMELLA A.A multifrequency analysis of radio variability of Blazars［J］.A&A，2004，419：485-500.

［9］ KUDRYAVTSEVA N A，PYATUNINA T B.A search for periodicity in the light curves of selected Blazars［J］.Astron Report，2006，50（1）：1-11.

［10］FAN J H，LIU Y，YUAN Y H，et al.Radio variability properties for radio sources［J］.A&A，2007，462：547-552.

［11］STEVENS J A，GEAR W K.Variations in the broad-band spectra of Bllac objects：Millimetre observations of an X-ray-selected sample［J］.MNRAS，1999，307（2）：403-412.

［12］TREVESE D，KRON R D，BUNONE A.Continuum variability of active galactic nuclei in the optical-ultraviolet range［J］. ApJ，2001，551（1）：103-110.

［13］WEBB W，MALKAN M，SCHMIDT G，et al.The wavelength dependence of polarization of active galaxies and quasars［J］. ApJ，1993，419：494-514.

［14］CHENG K S，FAN J H，ZHANG L.Basic properties of gamma-ray loud blazars［J］.A&A，1999，352：32-38.

［15］KAWAKATU N，IMANISHI M，NAGAO T.Anticorrelation between the mass of a supermassive black hole and the mass accretion rate in type 1 ultraluminous infrared galaxies and nearby QSOs［J］.ApJ，2007，661（2）：660-671.

［16］GU M F，CHEN Z Y，CAO X W.MBH-σ relation in sloan digital sky survey flat-spectrum radio quasars［J］.MNRAS，2009，397（3）：1705-1710.

【责任编辑：陈 钢】

Analysis on the long-term periodicity of Blazar 3C454.3 by α-F circle

YUAN Yu-hai，ZHANG Xin-yu，GUO Ning-li，ZHANG Guan-jun
（School of Physics and Electronic Engineering，Guangzhou University，Guangzhou 510006，China）

In the radio band，the relationship between the emission spectrum（α）and flux density（F）can demonstrate the emission theory and process.In this paper，we chose a Blazar with enough data from UMRAO （the University of Michigan Radio Observatory）to calculate the spectrum（α）and flux density（F）.We obtained 162 spectral indices（α），which come from-0.339±0.038 to 0.517±0.013，with the average value ¯α=0.171±0.217.There were anti-correlations between α and F：α=（-0.057±0.004）F14.5+0.758± 0.039，with the correlation coefficient r=-0.778，the chance P＜0.01%.There are two obvious elliptic curves lie in the distributions between α and F；the time spans of two elliptic curves were 5.82 years and 6.71 years；The time spans of the elliptic curves are consistent with the long-term periodicity optical variability.

Blazar；individually；3C454.3；spectrum

P 141

A

1671-4229（2016）03-0030-04

2016-02-26；

2016-03-10

国家自然科学基金资助项目（11403006）

袁聿海（1980-），实验师，理学博士.E-mail：yh_yuan@gzhu.edu.cn