二维光电影像测量仪系统摄像机标定技术
2016-09-22刘娟秀易茂丽
刘 霖 陈 祥 刘娟秀 罗 颖 凌 云 黄 田 易茂丽
二维光电影像测量仪系统摄像机标定技术
刘 霖 陈 祥 刘娟秀 罗 颖 凌 云 黄 田 易茂丽
本文针对二维光电影像测量仪中的摄像机标定,提出一种基于张正友标定算法的改进摄像机标定方法。该方法通过人工选点,得到需要检测的角点区域,接着利用Harris算子得到待测角点的初始位置,再根据灰度矩对所有角点进一步精确定位。最后利用张正友平面标定方法进行标定。实验表明,该方法对棋盘格角点位置定位较传统方法要好,最后标定的数值精确度较高,在二维光电影像测量系统中具有很高的实用性。
随着工业生产力的不断发展,对产品质量的追求也越来越高。如何快速准确地检测产品的质量已经是很多企业正面临的问题。基于光电图像处理的影像测量仪由于其具有非接触、自动化、可测微小物体、精度高等优点,使其成为装备制造业中质量控制中不可或缺的配套仪器。
二维光电影像测量系统主要建立在机器视觉检测技术基础上。摄像机标定是光电影像测量仪中一个重要的研究课题。相机标定就是根据一组已经空间位置的点与其图像对应点求解相机参数的过程。摄像机标定是计算机视觉系统实现的前提和基础。它是影像测量仪进行物体测量的首要步骤,是二维图像获取三维空间信息的关键和必要步骤。在影像测量仪系统乃至其他图像测量或者机器视觉应用中,摄像机参数的标定都是非常关键的环节,其标定结果的精度及算法的稳定性直接影响摄像机工作产生结果的准确性。
摄像机标定一直以来受到国内外学者的关注。传统的方法有DLT方法(直接线性变换方法),R.Tsai的RAC方法,张正友的平面标定方法,孟晓桥、胡占义的圆标定方法,吴毅红等的平行圆标定方法等。不依赖标定参照物的摄像机标定方法称为自标定方法。自标定方法非常灵活,但并不成熟,很难得到稳定的结果,在需要较高精度的应用场合应用较少。张正友的平面标定方法是介于传统标定方法和自标定方法之间的一种方法。它既避免了传统方法设备要求高,操作繁琐等缺点,比自标定方法精度高,目前得到广泛的应用。
在使用张正友标定法进行标定过程中,对棋盘格角点的检测是至关重要的一步,现在也有很多角点检测方法如Moravec角点检测算法、FAST角点检测算法、Harris角点检测、Shi-Tomasi算法。传统意义上的角点检测因为受图像数字特性影响,只能有一个像素的精度。这样的精度不能满足影响测量仪对精度的要求。为了提高角点检测的精度,往往还需要在像素级别的角点上对角点进行进一步亚像素定位。本文在张正友角点检测算法基础上,利用Harris算子和灰度矩相结合方法改进角点的检测精度,使整个标定过程精度得到提高。
摄像机标定
摄像机模型
摄像机模型一般采用针孔模型。在摄像机成像过程中,通常涉及到多个坐标系。它们分别是世界坐标系、摄像机坐标系和图像坐标系,图像坐标系又分为图像物理坐标系和图像像素坐标系。最后的成像公式可变为:

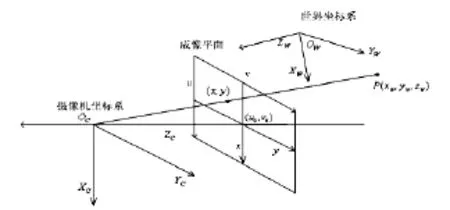
图1 摄像机成像模型
其中,[Xw,Yw, Zw,1]为P点在世界坐标系下的齐次坐标,[u,v,1]为投影点p在图像坐标系下的齐次坐标,s为一任意非零尺度的比例因子,旋转矩阵R与平移向量t称为摄像机的外部参数矩阵,A为摄像机内部参数矩阵:

图2 本文所用标定板
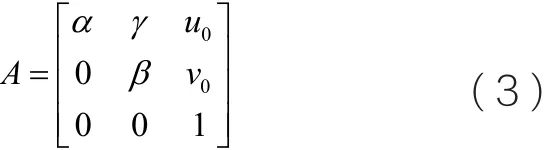
其中,(u0,v0)为图像中心点在图像坐标系中的坐标,α与β分别为图像坐标系中水平与垂直方向上的尺度因子,γ为两个坐标轴的不垂直因子理想情况下摄像机定标就是要求解这内外总共11个未知量。
角点综合检测方法
本文采用张正友平面标定方法,所用标定板为棋盘格标定板,如图2所示。要进行精确标定,需要对角点进行精确检测。
算法的第一步是用人工选点的方法确定待测角点的区域。
Harris角点算子
Harris算子是C Harris和M J Stephens在1988年提出的一种基于信号的点特征提取算子。这种算子受信号处理中自相关函数的启发, 出与自相关函数相联系的矩阵M。M矩阵的特征值是自相关函数的一阶曲率,如果两个曲率值都高,那么就认为该点是点特征。Harris算子的使用和证明已在文献中介绍。
Harris算子是一种有效的点特征提取算子,其优点有计算简单、提取的点特征均匀且合理、稳定。在角点检测中大量使用。但其只能获得像素级的坐标值。
本文对由人工点选得到的图像矩阵,通过Harris角点检测算子,可以得到角点的像素级坐标值,记为(u0, v0)。
灰度矩精确定位算法原理
灰度矩是由Tabatabai首先提出,最初用于边缘定位。其基本原理就是假设实际图像中的实际边缘分布与理想阶跃边缘模型的灰度矩保持一致,即矩不变性。在进行角点检测时,灰度矩角点定位原理与灰度矩边缘定位类似。即假设实际图像的实际角点与理想角点模型的灰度矩保持一致。
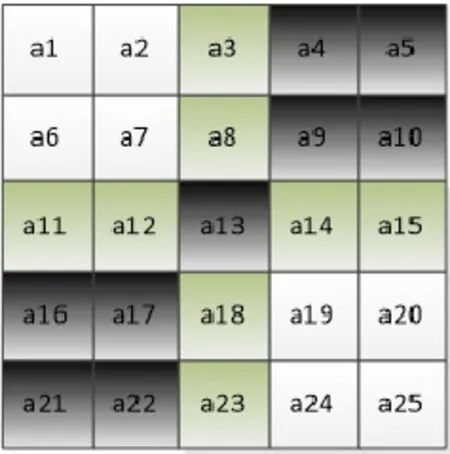
图3 角点近似模型

图4 二维理想角点模型
对于本文所要研究的数字图像I(i,j)来说,图像中目标区域S的p阶灰度矩的定义为:

式中,n为区域S中的像素点数
根据算子计算效率和精度,本文采用5x5的模型。图3为经过Harris算子检测到的角点近似模型,在图中,标号为a13的点检测到的角点。其精确度为1个像素。根据灰度矩近似原理,可以得到如图4的理想阶跃模型。设其真实角点位于(u,v)处,其中(u,v)的位置在a13这个像素内,为亚像素角点。根据棋盘格特点,整个模型将会被角点分为4个区域。整个模型可用4个参数表示,角点横坐标u,角点纵坐标v,区域1和区域3的灰度值h1,区域2和区域4的灰度值h2,即:
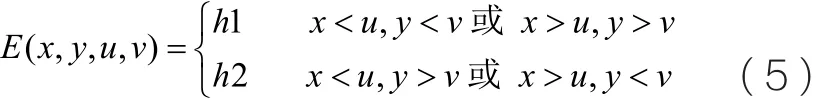
设每个像素点的单位长为d=1,则模型整个区域在(0,0)到(5,5)范围内。则理想阶跃模型中灰度矩可以表示为:

一共有4个未知数:u,v,h1,h2联立求解下列方程组:


图5 真实图像角点模型

图6 二维理想角点模型
可以求得h1,h2,和S。
得到S时,我们可以得到关于横坐标u和纵坐标v的关系式,即:

其中2<u<3,2<v<3。在这条曲线上的点都满足两种模型的灰度矩相等,都可以满足一定的数值精度。
为了进一步确定u和v的具体数值,得需一个约束条件。本文采用在一维上的灰度矩平衡来确定横坐标u。取5x1的理想阶跃模型,如图5、图6所示。
类似以上分析,整个模型可用3个参数表示,角点横坐标u,u左边区域灰度值h3,u右边区域的灰度值h4,即:

由式12可得其灰度矩方程:
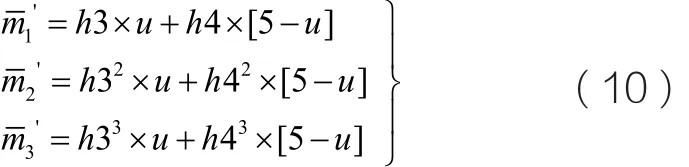
解方程组,可以得到u。
最后,将所解得的u代入式(13),可以得到精确的角点坐标(u,v)。注意这只是在理想模型的角点坐标。要得到在图像坐标系的坐标,有以下变换:

其中(u0, v0)为Harris算子得出的角点坐标。(u,v)为在灰度矩理想阶跃模型下的坐标,(u', v')为最后得到的精确坐标值。
张正友平面标定方法
标定模型
本文采用的摄像机标定模板为平面模板,如图2所示,模板为棋盘格。对任意的三维点,可以假设平面模板位于世界坐标系的x o y平面,即z=0。
设平面靶标上的每个特征点的坐标为(xwi,ywi,zwi),在摄像机坐标系下的坐标为(xci,yci,zci),记图像坐标为(ui, vi),令z=0有:
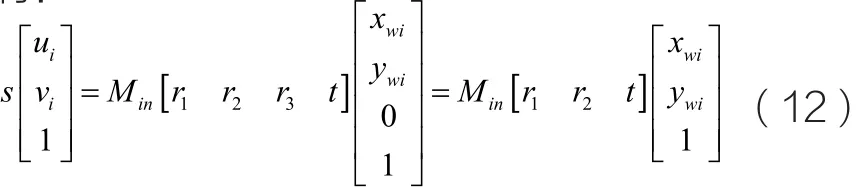
其中,s 为常数,Min是摄像机的五参数内参矩阵,精简上式为:
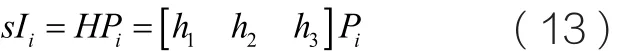
式中,Ii=(ui, vi,1)为点Pi的图像坐标,Pi=(xwi,ywi,1)为点Pi在靶标坐标系下的坐标,[h1h2h3]是从笛卡尔坐标到图像坐标的单应性矩阵。
参数求解
由式(13),利用旋转矩阵的特性得到如下式(14)和式(15)两个约束方程:

对于采集到的N幅图像,得到N组方程,可以联立2N个方程。从而求出内外参数。
标定过程总结
张正友标定的过程如下:
(1)在未畸变模型下,对内参数的5个参数标定获得线性初值;
(2)利用获得的线性初值对畸变系数进行标定;
(3)利用标定出来的非线性参数重新进行线性标定;
(4)重复第二步到第三步的步骤,直到线性参数和非线性参数收敛为止。
第一步进行标定时,因为摄像机的畸变未能纳入考虑范围,得到的结果精度较低,而第二步标定出来的非线性参数的精度也不能达到要求,只有对标定出来的线性参数进行非线性计算,直到线性和非线性参数都收敛才能得到最精确的值。
实验验证与分析
为了验证本文方法的正确性和有效性,文中采用C++进行界面编程,对算法进行验证。验证步骤如下:
(1)选定相机和镜头,在不同的角度对同一棋盘格拍图;
(2)用人工选点的方法得到待检测的角点区域。利用Harris算法进行角点检测。得到角点的初始位置;
(3)针对初始位置,用灰度矩算法对角点进行亚像素定位。得到角点的亚像素坐标;
(4)用得到的亚像素角点数据进行张正友相机标定。得到相机标定结果。
在本次实验中,相机分辨率为2590 × 1942。棋盘格标定板中一个格子的边长设计为20mm。为了结果的准确性,一共标记20张图。如图7所示。

图7 标记图像所用的20张图
根据半自动角点检测步骤,人工选定棋盘格角点外接矩形中两个方向的格子数分别为9和7。然后进行Harris角点检测和灰度矩角点亚像素定位,图8为其中一张图采集到的棋盘格图像角点的检测结果。可以看出,检测结果非常接近实际角点位置。
图9为角点局部放大的图像。图中每一个方格代表一个像素点。十字交点为通过本文方法检测到的角点。该角点位置位于一个像素内,精度为亚0.01个像素。可以看出,优化后的结果比Harris算子得到的像素级别角点位置更接近实际角点的位置。
更多的角点变化结果,见表1。可以看到,Harris算子得到的角点坐标为像素级别,精度为1像素,本文中利用灰度矩改进算法得到的坐标为亚像素级别,精度为0.01像素。本文方法更能体现角点的实际位置。

表1 不同算法对应的角点坐标对比
最后,利用角点数据进行张正友标定结果如表2所示。

表2 不同标定方法算法标定结果比较
根据官方给的相机资料,相机的焦距为3730mm。可见,用灰度矩算出的角点位置更符合实际情况,得到的相机参数也更准确。
结语
在本文研究的标定中,使用半自动的角点检测方法,手动框选角点范围,然后使用Harris算子进行角点初步定位,接着利用灰度矩算法对角点位置进行优化,得到亚像素级别的角点位置,最后利用张正友标定法进行标定。实验表明,将灰度矩应用于相机标定中,可以得到比较好的角点检测效果,最后得到的标定结果的精度较高,满足在影像测量仪中对各个参数要求高的这一需求。
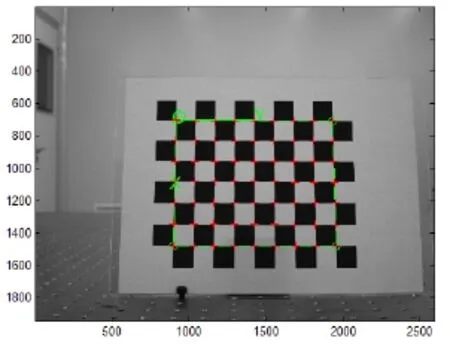
图8 角点检测结果图

图9 角点局部放大图
刘 霖1,2陈 祥2刘娟秀1,2罗 颖1凌 云1黄 田1易茂丽1
1.东莞成电术有精密技术有限公司;2.电子科技大学光电信息学院
10.3969/j.issn.1001-8972.2016.11.002
