一个共轭梯度优化方法及其在工程中的应用*

黄玲花

(广西财经学院 信息与统计学院，广西 南宁　530003)



一个共轭梯度优化方法及其在工程中的应用*

黄玲花

(广西财经学院 信息与统计学院，广西 南宁530003)

给出一个三项共轭梯度方法，该方法具有如下特点：1)搜索方向在不需要任何线搜索的条件下具有充分下降性；2)搜索方向具有自动属于一个信赖域的特点；3)新方法不但拥有梯度值信息还拥有函数值信息；4)方法对一般函数拥有全局收敛性.数值检验结果表明新方法更具竞争性.

共轭梯度；充分下降；收敛性

0　引言

(1)

其中f(x):Rn→R是连续可微函数.无约束最优化问题来源于众多实际问题，具有广泛的应用背景，此问题的求解方法有很多种：牛顿法、拟牛顿法、信赖域方法和共轭梯度法等等，这些优化方法能为求解其他优化问题提供强有力的理论支持.共轭梯度方法具有结构简单、计算机存储量小和高效率的特点，因而被广泛应用.该方法的迭代公式是：xk+1=xk+αkdk,k=0, 1, 2,…

其中xk称为第k次迭代点，αk>0是由线搜索产生的步长，dk是搜索方向，定义形式为

(2)

其中gk=▽f(xk)和gk+1=▽f(xk+1)是函数f(x)在xk和xk+1的梯度值，‖·‖表示欧式向量范数.该方法数值表现优越特别适合大规模优化问题，也常常被人们用于实际的问题中，是研究最为热门的共轭梯度公式之一.但是PRP方法的收敛性不理想，对于一般函数在弱Wolfe-Powell线搜索下的全局收敛性一直没有得到证明，是一个开放的问题.鉴于此，许多学者希望发现数值表现能与PRP相媲美同时收敛性质又比它优越的方法，许多成果可参见文献[8-15]等.研究发现，该方法在非精确线搜索下对一般函数收敛性不好的一个主要原因在于它不能保证充分下降性，充分下降性是指对所有k，式(3)的不等式成立

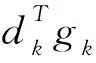
(3)

研究发现该性质在收敛性的理论分析中起着重要作用.基于PRP方法，为保证(3)关系式的成立，Zhang[16]等给出了一个三项共轭梯度方法，方向为

(4)

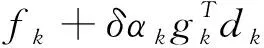
(5)

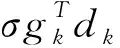
(6)

其中δ∈(0,1/2),σ∈(δ,1)，受(6)的启发，Yuan[17]等给出了下面的共轭梯度方向

(7)

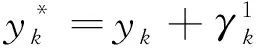
(8)

容易看出新公式不但拥有梯度值还拥有函数值信息.

1　算法

算法1(修改的共轭梯度算法)

步骤0：给定x0∈Rn，c∈(0,1),δ∈(0,1/2),σ∈(δ,1)和终止参数ε>0.令d0=-g0=-▽f(x0)，

置k：= 0.

步骤1：若‖gk‖≤ε，停止.

步骤2：寻找满足(5)和(6)的步长αk.

步骤3：令xk+1=xk+αkdk,如果‖gk+1‖≤ε，停止.

步骤4：利用公式(8)计算搜索方向.

步骤5：置k：=k+1，转步骤2.

2　充分下降性、信赖域性质和全局收敛性分析

下面证明修改的三项公式方向具有充分下降性和信赖域的性质.

引理1 对k≥0，修改的三项公式的搜索方向满足

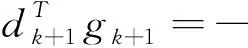
(9)

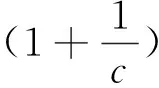
(10)

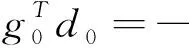
(9)成立.对于关系式(10)，根据(8)式，当k=0，(10)显然成立，当k≥1时，我们有

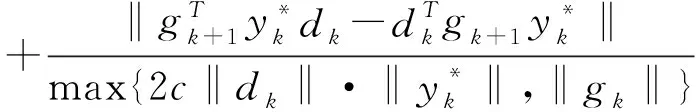
因此(10)成立.证毕.

假设条件(A)：i) 水平集Ω={x∈Rn:f(x)≤f(x0)}有界.

ii)f在Ω上有下界且连续可微，它的梯度g满足Lipschitz条件，即存在常数L>0满足

‖g(x)-g(y)‖≤L‖x-y‖,∀x,y∈Ω

(11)

证明：根据WWP线搜索的关系式(6)和Lipschitz条件(11)，得到

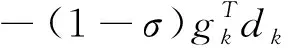
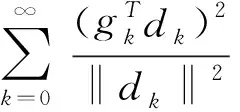
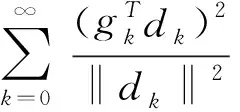
(12)

3　数值结果

为了验证算法的有效性，给出数值检验结果，检验函数是在工程领域经常用到的Benchmark问题，这些问题列举如下.

1)Spherefunction.

2)Schwefel'sfunction.

3)Rastriginfunction.

4)Schwefelfunction.

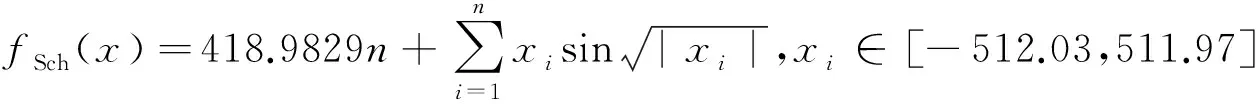
x*=(-420.9678,-420.9678,…，-420.9678),fSch(x*)=0

5)Griewankfunction.

上述的Benchmark问题可从下述的网站中找到：http://www.cs.cmu.edu/afs/cs/project/jair/pub/volume24/ortizboyer05a-html/node6.html

实际计算中，参数选取如下：c=0.5,ε=10-5,δ=0.1,σ=0.9,停止准则采用Himmeblau准则：

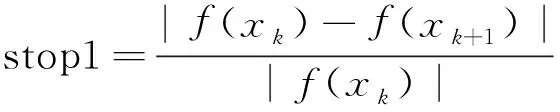
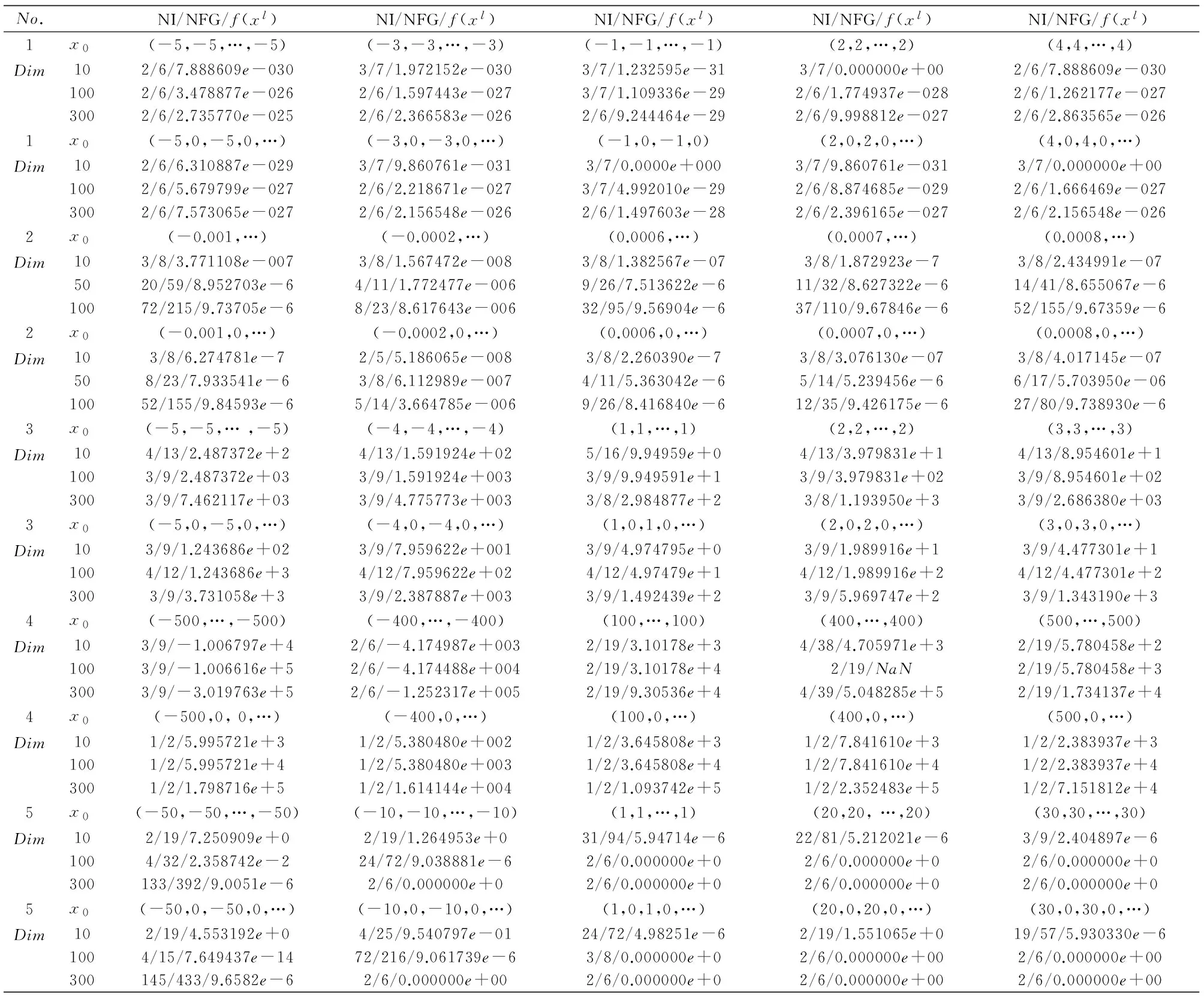
表1　算法1的数值结果

从表1结果可以看出，对给定的终止条件，算法1能大部分成功求解，这说明了方法的有效性.但是对一些问题，数值表现不是很理想，这说明方法具有待改进的地方.特别是初始点的选择方面，有待进一步的研究.

上述Benchmark问题是工程中的常用问题，我们利用这些问题进行验证方法的有效性，目的是为了证实算法在实际领域中具有一定的应用背景.当然还有其他更多的应用问题有待进一步研究和探讨.

4　结论

本文给出一个修改的三项PRP方法，证明了方法对一般函数在WWP线搜索下具有全局收敛性，并给出了数值检验结果，相对于通常的PRP方法和三项PRP方法可得出如下结论：

1)与通常的PRP方法相比较，新方法不但具有充分下降性，还具有信赖域的特点，同时能保证对一般函数在WWP线搜索下的全局收敛性，数值结果也具有竞争性；

2)与通常的三项PRP方法相比较，新方法具有了信赖域的特点且对一般函数在WWP线搜索下的全局收敛性，同时拥有梯度值信息和函数值信息；

3)与文章Yuan[17]相比较，将方法推广到一般的光滑优化方法中，且两种方法所具有的函数值信息不同.

[1] Y. Dai , Y. Yuan. A nonlinear conjugate gradient with a strong global convergence properties [J]. SIAM J. Optim, 2000 (10):177-182.

[2] R. Fletcher. Practical Method of Optimization, Vol I: Unconstrained Optimization [M]. 2nd edition, Wiley, New York, 1997.

[3] R. Fletcher , C. Reeves. Function minimization bu conjugate gradients[J].Compute. J, 1964 (7): 149-154.

[4] M. R. Hestenes , E. Stiefel. Method of conjugate gradient for solving linear equations, J, Res [J]. Nat. Bur. Stand, 1952 (49):409-436.

[5] Y. Liu , C. Storey. Effcient generalized conjugate gradient algorithms, part 1: theory[J].Journal of optimization theory and Application ,1992 (69).

[6] E. Polak , G. Ribiere.Note sur la xonvergence de directions conjugees[J]. Rev. Francaise informat Recherche Operatinelle , 3e Annee, 1969 (16).

[7] B. T. Polyak.The conjugate gradient method in extreme problems [J].USSR Comp Math Math Phys,1969 (9): 94-112.

[8] W. W. Hager , H. Zhang. A new conjugate gradient method with guaranteed descent and an e?cient line search [J]. SIAM Journal on Optimization, 2005 (16): 170-192.

[9] W. W. Hager , H. Zhang.Algorithm 851: CGDESCENT, A conjugate gradient method with guaranteed descent[J]. ACM Transactions on Mathematical Software, 2006 (32): 113-137.

[10] G. Li, C. Tang, Z. Wei.New conjugacy condition and related new conjugate gradient methods for unconstrained optimization problems[J]. Journal of Computational and Applied Mathematics, 2007(202):532-539.

[11] Z. Wei, G. Li, L. Qi. New nonlinear conjugate gradient formulas for large-scale unconstrained optimization problems[J].Applied Mathematics and Computation, 2006 (179):407-430.

[12] Z. Wei, G. Li, L. Qi.Global convergence of the PRP conjugate gradient methods with inexact line search for nonconvex unconstrained optimization problems[J].Mathematics of Computation, 2008 (77): 2173-2193.

[13] Z. Wei, S. Yao, L. Liu. The convergence properties of some new conjugate gradient methods[J]. Applied Mathematics and Computation, 2006 (183):1341-1350.

[14] G. L. Yuan. Modified nonlinear conjugate gradient methods with suffcient descent property for large-scale optimization problems[J]. Optimization Letters, 2009 (3): 11-21.

[15] G. L. Yuan , X. W. Lu. A modified PRP conjugate gradient method[J]. Annals of Operations Research, 2009 (166): 73-90.

[16] L. Zhang, W. Zhou, D. Li.A descent modified Polak-Ribi`ere-Polyak conjugate method and its global convergence[J]. IMA Journal on Numerical Analysis, 2006 (26) :629-649.

[17] G. Yuan, Z. Wei, G. Li. A modified Polak-Ribière-Polyak conjugate gradient algorithm for nonsmooth convex programs[J].Journal of Computational and Applied Mathematics, 2014 (255):86-96.

[18] J. Z. Zhang, N. Y. Deng, L. H. Chen, New quasi-Newton equation and related methods for unconstrained optimization[J]. Journal of Optimization Theory and Application, 1999 (102):147-167.

[责任编辑苏琴][责任校对黄祖宾]

A Conjugate Gradient Optimization Method and Its Applications in Engineer

HUANG Ling-hua

(DepartmentofMathematicsandStatistics,GuangxiUniversityofFinanceandEconomics,Nanning530003,China)

In this paper, a conjugate gradient method is proposed. The given method possess the following features: 1) The search direction possesses the sufficient descent property; 2) The search direction belongs to a trust region;3) The new method has not only the gradient value but also function value;4) The presented method has the global convergence for general functions. Numerical results turns out the new method is more competitive to the normal method.

conjugate gradient；sufficient descent；trust region；convergence

2016-03-20.

广西财经学院数量经济学重点实验室项目开放性课题(2014SYS05)；国家自然科学基金项目资助(11161003).

黄玲花(1965-)，女，广西财经学院信息与统计学院副教授，研究方向:应用数学.

O224

A

1673-8462(2016)02-0063-05