BP神经网络技术在神木气田水平井产能预测中的应用

刘鹏飞，文开丰，高君微，王　超，杨国平

（中国石油长庆油田分公司第二采气厂，陕西西安　710200）

BP神经网络技术在神木气田水平井产能预测中的应用

刘鹏飞，文开丰，高君微，王超，杨国平

（中国石油长庆油田分公司第二采气厂，陕西西安710200）

传统水平井产能预测计算由解析解法与半解析解法确定，有极大的局限性，所以在应用中常常预测不够准确。本文选择BP神经网络算法，通过输入信息神经网络权值和阀值作用，计算各层误差，依次对权值和阀值进行修改，达到高精度、快速逼近样本的目的。最后用训练好的网络来进行神木水平井产能预测。仿真结果表明，神经网络算法应用效果显著，预测值与实际值相对误差在±10%之内，能够满足工程精度要求。

水平井；神经网络；产能预测

神木气田现已建成16.7×109m3/a，水平井开采技术已成为神木气田高效、经济开发的重要技术。水平井产能是气田开发决策的一个重要参数，因此能否准确的获得水平井产能成为气田开发的一个重要问题。神木气田具有非均质性强，砂体发育不连续，储层深处的含气特性与近井地带差异大等特点，地质条件复杂。水平井无阻流量与储层物性参数之间呈复杂非线性关系，传统计算无阻流量的解析解法与半解析解法大多做了相关理想假设，计算精度不高。人工神经网络方法是解决复杂非线性问题的有效方法，在解决非线性问题时，表现出极大的灵活性和自适应性，能达到各主要因素对无阻流量预测的高精度拟合。笔者采用BP神经网络技术在综合考虑各主要地层物性因素的基础上建立了产气水平井产能模型，并使用训练好的产能模型对神木已完钻水平井进行产能预测［1，2］。

1　BP神经网络计算方法

设置由三层的神经元网络构成（见图1），BP模块以特有的导师学习方式进行训练［3-6］。

图1　三层BP网络

BP算法运算步骤分两步，首先是从下至上，导入神经单元网络权值和阀值作用，依次递送到输出层。再是从上至下，演算出各层误差，依次对权值和阀值进行修改，并将误差向下传递。两个过程反复交替，直到收敛为止。

1.1正向传播-模型结构由输入层经隐含层向输出层传播

设输入层、隐含层、输出层节点数分别为m、l、n。输入向量为X=（x1…xi…xm），对应希望输出向量为T= （t1…tk…tn）。根据BP神经元模型原理，隐含层各神经元的激活值：

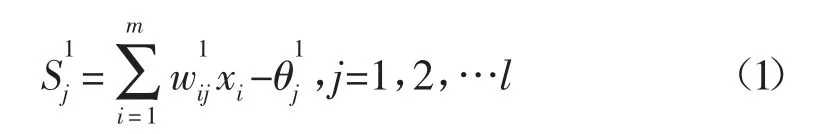
激活函数常采用S型的sigmoid函数：

将激活值代入激活函数可得隐含层第j节点的输出值：

1.2反向传播-演算出的误差由输出层经隐含层传向输入层

BP学习方法应用的是δ学习规则，即利用误差的负梯度来调整连接权，使其输出误差单调减少。

输出层的校正误差为：

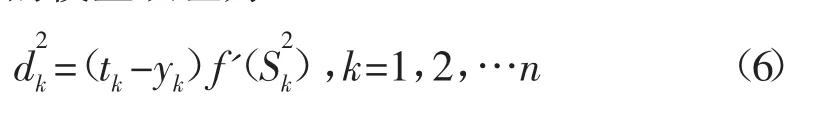
隐含层的校正误差为：

对于输出层至隐含层连接权和输出层阀值校正量分别为：

隐含层至输入层连接权和隐含层阀值校正量为：

针对Q组设置模型：

其对应希望输出值为：

通过网络对应输出端的实际输出值为：

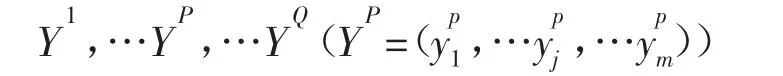
则网络全局误差：

当E小于给定精度ε时，即E＜ε，网络近似收敛到最优值。

2　水平井产能预测模型的构造

对于神木气田封闭气藏，气井的生产只能达到拟稳定状态，渗流达到拟稳定流动后的水平井产能二项式也应与渗流达到拟稳定流动后的直井产能二项式具有相同的表达式，但影响二项式系数的参数不同，即A 和B值不同［7］。水平井在圆形供气面积上的拟稳态流动方程为：

二项式产能方程：

气井水平井二项式产能方程的A和B值：

其中：

式中，Qg为无阻流量，104m3/d为气体黏度，mPa·s为气体压缩因子；T为气层温度，K；PSC为标准情况下大气压，MPa；K为气层渗透率，10-3μm2；h为气层有效厚度，m；TSC为标准情况下气层温度，K；re为供给半径，m；rw为井筒半径，m；Ssa为气井视表皮系数；B为气体体积系数，m3/m3；γg为相对密度；PR为原始地层压力，MPa；AC'为圆形供气面积，取0.75，矩形供气面积取0.738；C'为形状因子换算系数。

由以上分析可知，直接影响水平井无阻流量大小的指标有钻遇储层有效厚度、地层渗透率、排驱半径、流体黏度、井半径、原始地层压力、气井表皮系数、含气饱和度、气层孔隙度等因素，气井的产能与各因素之间是一个非线性的函数关系。采用数值模拟“正交试验”法研究分析［8-11］，影响气井产能的主要因素有原始地层压力、渗透率、孔隙度、饱和度、钻遇有效储层厚度、表皮系数，共6个主要因素。

用VB语言实现了神经网络计算方法算法程序，并建立水平井产能与各因素之间的函数关系式：

（1）选用3层BP网络模型。

（2）BP神经网络模型输出层节点构造：原始地层压力、渗透率、孔隙度、饱和度、钻遇储层有效厚度、表皮系数6个因素作为输入层节点；输出层节点有1个：水平井产能。

（3）BP神经网络模型中间层的节点数与输入层/输出层节点数的经验公式：

式中：s为隐含层节点数；m为输入层节点数；n为输出层节点数。计算结果经四舍五入取整。将m=6，n= 1带入，得s=5。故隐含节点数取5比较合理，建立的预测气井产能的三层神经网络模型为6×5×1，经多个实例验证，利用上式确定隐含层节点数的初值比较可靠，能满足训练需要。

3　水平井产能预测模型的应用实例及效果

截止目前，神木气田共完钻水平井13口，主力开发山西组和太原组，平均水平段长度1 135 m，砂岩钻遇率79.3%，平均无阻流量25.12×104m3/d。选择已完钻的11口水平井作为样本井进行训练学习（见表1），两口井作为预测井。运用文中构造的神经网络模型，在经过105次循环迭代后收敛，全局误差为E=0.67×10-3。

表1　　进行样本训练的各水平井参数表

运用所建立的神经网络预测模型，输入双平L和双平M两口预测井的相关参数，预测该气田其他两口水平井的产能，其结果（见表2）。

表2　产能预测结果表

由上述结果表明所建立的神经网络系统具有很好的稳定性，预测精度高，预测值与实际值相对误差在±10%之内，能够满足工程精度要求。

4　结论

应用神经网络方法预测水平井产能是可行的，解决了水平井产能与其参数之间的非线性问题。应用该方法预测，神木气田两口水平井预测值与实际值相对误差都在工程要求之内。该方法可以作为水平井产能预测的一种有效手段，为气田开发部署提供了理论依据。

［1］ 王黎，孙倩倩，张凌筱，等.BP人工神经网络在塔河油田产能预测中的应用［J］.中国石油和化工，2012，10（2）：50-53.

［2］ 许敏，赵粉霞.神经网络法在气井产能预测中的应用［J］.天然气工业，2000，20（3）∶73-75.

［3］ 彭敦陆，徐士进，王汝成，等.神经网络专家系统在预测单井日产量上的应用研究［J］.石油实验地质，1999，21（2）∶156-160.

［4］Philip F，Coveney P V，Hughes T L.Predicting quality and performance of oilfield cements with artificial neural networks and FTIR spectroscopy［C］.SPE 30079，1995.

［5］ 胡守仁.神经网络应用技术［M］.长沙∶国防科技大学出版社，1993.

［6］ 许玲，陈德民，赖枫鹏.气井新井产能预测的神经网络方法研究［J］.油气井测试，2008，17（3）∶12-14.

［7］ 余林瑶.苏里格气田水平井产能评价研究［D］.北京∶西南石油大学，2012.

［8］ 李琴.低渗致密气藏压裂水平井产能评价方法优化［D］.北京∶中国地质大学（北京），2013.

［9］ 曾凡辉，郭建春，徐严波，等.压裂水平井产能影响因素［J］.石油勘探与开发，2007，（4）∶474-477.

［10］ 赵文军，史福军.气井产能核实方法研究［J］.石油化工应用，2011，30（9）∶63-66.

［11］ 张枫，等.有限导流裂缝水平井产能研究［J］.天然气地球科学，2009，20（5）∶817-821.

TE328

A

1673-5285（2016）05-0064-04

10.3969/j.issn.1673-5285.2016.05.017

2016－04-05

刘鹏飞，男（1985-），甘肃天水人，硕士研究生学历，工程师，现从事油气藏工程动态分析及数值模拟方面的工作，邮箱：lpf2003021218@126.com。