转动物体的动能和“溜溜球”的机械能守恒
2016-09-20王岱川
王岱川
(电子科技大学实验中学 四川 成都 611730)

转动物体的动能和“溜溜球”的机械能守恒
王岱川
(电子科技大学实验中学四川 成都611730)
借助转动物体的力学知识,对溜溜球的运动过程进行了分析和解释,证明其满足机械能守恒,且与圆盘沿斜坡滚动的过程具有相似性.
溜溜球转动惯量转动定律机械能守恒斜坡滚动
1 溜溜球的结构和运动
“溜溜球”是一种非常受中小学学生喜爱的玩具,有几十种玩法,比如:遛狗、睡眠、前抛、逃脱、摇篮、爬行者、升降机、卫星回收等等,这些丰富多彩的玩法中包含了中学所学的许多物理知识.常见的溜溜球有两种类型,第一种类型比较简单,其结构如图1所示[1],图2是溜溜球的剖面图.图1的左右两侧是两个对称的圆盘,半径为R,圆盘通过转轴固定连接,转轴半径r≪R,两个圆盘和固定连接的转轴构成了溜溜球的主体A,转轴上缠绕细绳C,细绳的一端固定在转轴上.
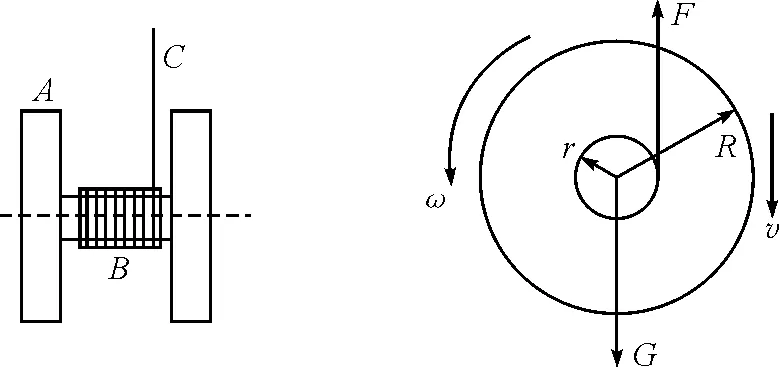
图1 溜溜球的结构 图2 下行时的受力分析
下面分析最基本的“下行上爬”运动[2].游戏者将细绳的另一端套在手指上,从高处释放溜溜球,溜溜球在重力和细绳拉力作用下匀加速下行,受力分析如图2所示(忽略空气阻力和摩擦力).由于细绳的约束,下行运动与细绳展开的速度相同,同时溜溜球沿轴心匀加速转动.当细绳全部伸展时,溜溜球的转动速度和下行速度达到最大,并突然“转向”,开始上爬,当爬到最高点时,又重新开始下行,但转动方向相反.之后溜溜球会自动下行上爬,由于阻力和摩擦力的阻碍,运动一段时间后逐渐停下来,如果每次“转向”时,轻往上提,补充损失的能量,则可反复“下行上爬”.
第二种溜溜球在图1的转轴上套上空轴B,转轴与空轴B之间通过轴承光滑连接,细绳空套在B上而不固定连接,但在缠绕时须一层一层用力缠紧.这种溜溜球阻力较小,转动速度更快,在下行结束时,并不立即上升,而是在底部持续转动,这种玩法称为“睡眠”.当手指轻轻上抖,触发溜溜球迅速上爬,称为“唤醒”.如果下落时用力往下甩,转动速度和持续运动的时间会明显增加,如果在“睡眠”时接触地面,溜溜球将沿地面滚动,游戏者收放细绳,则可完成“遛狗”“爬行”等玩法.

下面首先讨论转动物体的动能,然后带着上述问题分析溜溜球的运动,最后,与斜坡上圆盘的滚动过程对比.
2 均匀圆环和均匀圆盘的转动动能

(1)
由于圆环质量
m=2πrδρdr
(2)

图3 均匀圆环的动能
均匀圆盘可看作无数圆环构成,圆环宽度为dr,所有圆环具有同样的转动速度ω,设圆盘半径为R,圆盘质量为m=πR2δρ,则其动能为式(1)在[0,R]区间的积分,即
(3)
3 溜溜球的运动过程分析和机械能守恒
下面分析第一种结构的溜溜球的运动过程,设图2中溜溜球圆盘的半径为R,转轴的半径为r,总的质量为m.下行过程中溜溜球的质心加速度为aC,转动的角加速度为αr,细绳长度为h,由静止开始释放,线速度为v,角速度为ω,由于转轴和两个圆盘固定连接,角速度相同,可按式(3)计算溜溜球的转动惯量I和转动动能.由图2有
maC=mg-F
(4)

(5)
(6)
(7)
(8)
此时,溜溜球的动能包含向下的平动动能和转动动能,代入式(7)和式(8)得到

溜溜球为什么能自动上爬呢?细绳完全展开后,向下运动的惯性拉伸细绳,平动动能转化为细绳的弹性势能,至最大形变后平动速度降为零,细绳的弹性恢复使溜溜球向上加速,对理想的弹性体,细绳的弹性势能完全转化为向上的平动动能,转化结束的瞬时速度大小与细绳完全展开瞬间相同.但由于细绳不是理想的弹性体,转向后动能会有损失,这个转化过程在短时间内完成,游戏者的手指能感觉到短暂的抖动.另一方面,细绳完全展开后由于转动惯性,溜溜球继续沿原有方向转动,并将细绳反向缠绕在转轴上,实现快速“转向”,开始“上爬”运动.转化后的动能促使溜溜球“上爬”,由于转化过程中的动能损失和阻尼作用,爬升的高度不能达到初始位置.上升到最高点后重复下行过程,此时细绳在转轴上的缠绕方向改变,转动的方向与上一次下行的转动方向相反,游戏者可观察到最高点时,溜溜球转动逐渐停止,朝相反方向转动的现象.这样,溜溜球重复“下行-转向-上爬”的过程.若每次转向的时候,手指上提溜溜球,补充损失的动能,则可保持在相近的高度上下运行,完成持续的“下行上爬”的玩法.
“睡眠”和“唤醒”则体现了平动和转动的相互转化.在第二代溜溜球结构中,空轴B的质量和动能远低于A,B在下行过程中受缠紧的细绳的约束,但细绳末端是空套在B上的,而A通过轴承与B连接.达到底部后,平动动能也转化为转动动能,B在细绳末端的套结中转动,A在B中转动,轴承均匀光滑,A的转动速度高于B,转动中的摩擦阻力小于B,当B停止转动后A还能持续转动较长时间,溜溜球处于“睡眠”状态.在“睡眠”中,手指向上轻轻抖动,产生向上的初速度,溜溜球将迅速向上回收,这个“唤醒”过程触发了转动动能向平动动能的转化.而溜溜球的前抛、遛狗、爬行、猴子上树等玩法中,有更多平动和转动相互转化的现象.
4 斜坡滚动圆盘与溜溜球运动的相似性
从角度为θ的斜坡顶点由静止开始释放均匀圆盘,圆盘沿斜面向下滚动,圆盘半径为r,质量为m,斜坡高度为h,如图4所示.圆盘在滚动的过程中受重力G,斜面支持力N和摩擦力f,滚动速度为ω,圆盘质心的线速度为vC,质心的加速度为aC,圆盘角加速度为ar,则同样有ω=vCr,由于转动方向的切向速度与质心速度相反,所以aC=-rar.
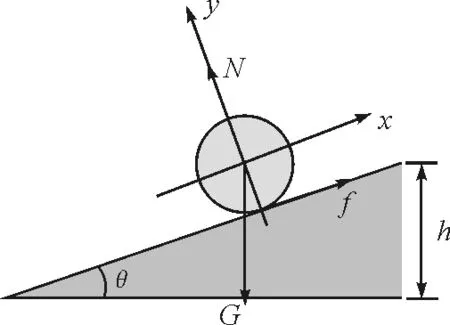
图4 圆盘沿斜坡滚动示意图及受力分析
重力沿y轴的分量与支持力平衡,沿x轴有
f-mgsinθ=maC
(9)
由转动定律
(10)
(11)
其中负号表示加速度方向沿x轴负方向.比较式(10)、(11)和式(5)、(6),当θ=90°时,在数值上相等(忽略x轴方向设定).
可见,圆盘的斜坡滚动与溜溜球的下行运动非常相似,溜溜球在水平方向不受力,而斜坡运动在垂直与斜面方向平衡,导致转动的力矩分别为细绳拉力和斜坡摩擦力,而受力分析、运动过程和运动参数则雷同.斜坡长度
运动到斜坡底部的时间
速度
代入式(11)化简后得到总动能为
可见斜坡滚动圆盘的机械能也守恒.
5 结论
溜溜球的运动过程中包含了平动和转动,体现了平动动能、转动动能和重力势能的相互转化.论文讨论了溜溜球的结构和常见运动,从平动物体的动能导出了均匀圆环和圆盘的转动动能,借助转动运动学中的转动惯量和转动定律,证明了溜溜球的运动过程中机械能守恒.对斜坡滚动圆盘的分析表明,溜溜球的下行运动与之相似,再次体现了两种动能和重力势能的转化,以及转化过程中的机械能守恒.
1郑俊,肖发新. 溜溜球的力学原理. 物理教师,2005(2):45
2杨全民.溜溜球的力学原理及运动过程分析.连云港师范高等专科学校学报,2001(2):72~74
3漆安慎,杜婵英. 普通物理学教程:力学(第三版).北京:高等教育出版社,2012. 170
2016-03-30)
