主干知识:承上启下,推陈出新
---由李庾南老师的一则教学案例说起
2016-09-20江苏省如皋市外国语学校马亮
江苏省如皋市外国语学校 马亮
主干知识:承上启下,推陈出新
---由李庾南老师的一则教学案例说起
在学生获得的众多数学知识中,有些知识是"终极"知识,对这类知识的学习到此为止,不再延续,这类知识我们一般称为边缘知识;有些知识是"中间"知识,是为后续学习而学习的知识,这类知识我们称之为主干知识.在初中阶段,数学的主干知识具有极强的延续性,它们一般都是对应版块的核心知识,不仅对本学段学习的影响很大,而且还会影响下一学段的数学及相关学科的学习.对这类知识的教学,我们应充分挖掘它们的自身价值,在获取主干知识的过程中将后续知识"生长点"进行"预埋";在新知教学中要用好已经获得的主干知识,让新知附着于主干之上,持续"有理有据"地生成.著名特级教师李庾南老师多次以"主干知识"的教学应用为例进行了教学展示,取得非常好的教学效果,现结合其著作《自学.议论.引导教学法》中的一则教学案例谈谈笔者对主干知识的认识,不足之处敬请各位同行专家批评指正.
一、案例简述
1.教学内容
等腰三角形的性质定理及推论.
2.过程简述
教师首先引导学生回顾了"相等的线段"、"相等的角"、"全等三角形"的含义,然后让学生按照图1中的虚线自主折叠等腰三角形纸片ABC,找出其中能够重合的线段、角和三角形,并将发现的结论在全班交流.
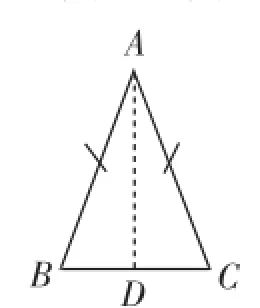
图1
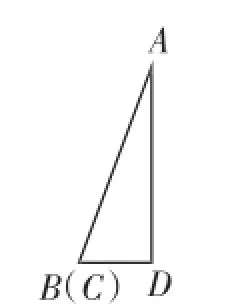
图2
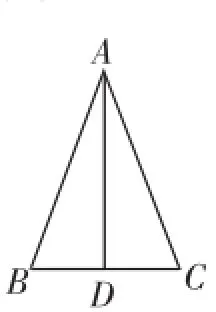
图3
通过折叠,学生非常直观地感知到图2中存在的结论:①AB、AC重合;②BC被分成了能重合的两条线段;③∠BAC被分成两个重合的角;④平角∠BDC被分成了两个重合的直角;⑤△ABC被分成两个完全重合的直角三角形.
在找到重合的线段、角和三角形后,教师引导学生将这些结论抽象为符号语言:①AB=AC;②BD=CD;③∠BAD=∠CAD;④∠BDA=∠CDA=90°;⑤△ABD≌△ACD.
接下来,教师请学生利用所学的知识证明这些结论,并给出完整的推理过程.根据轴对称的知识,学生很快利用图3给出了证明.至此,教师和学生一起概括出等腰三角形的性质定理及推论.
3.简要分析
在李老师设计的教学中,学生经历了"动手操作"、"发现结果"、"猜想结论"、"验证结论"、"抽象性质"等多个活动.这些活动紧紧串在一起,活动衔接严丝合缝,前一个活动是后一个活动的基础,后一个活动是前一个活动的延续.将这些活动整体串联在一起的是本节课的主干知识---轴对称的性质,这是每一个活动得以延续的"四基"保证.轴对称带来的图形重合给了学生"相等或全等"的直观感知,这是知识的铺垫;能够折叠使之重合,这是技能的保证;图形的重合与符号下的相等或全等的转化,是抽象思想的延续;折叠对应着重合,重合关联着相等,相等指向了全等,这些都是学生在探究轴对称性质时积累下的活动经验.很显然,为了让轴对称这一主干知识发挥其"承上启下,推陈出新"的价值,李老师从学生的认知起点出发,将教学的起点定位在旧知的延续应用之上,将教学的终点定格在主干知识的充实与完善上,教学效果是显著的.
二、主干知识的特点
主干知识,一般是因为数学知识体系的发展过程或解决实际问题的需要而引入的,属于学生"应知,应会,应用"的知识.在人教版的六册初中数学教材中,每册都有着主干知识的分布.因此,在教学中,我们应时刻关注这些主干知识,将其作为教学设计与教学实施的核心.为让我们更好地落实主干知识的教学,我们先来分析一下这些知识的特点.
1.主体性
主干知识是学生获取新知和解决问题的重要工具,理应成为教学的主体.虽然现行教材没有将主干知识集中呈现,零散的分布丝毫不影响它们的地位及作用,反而更加有利于单位教学时段内集中"优势兵力"加以突破,凸显其在教学中的主体地位.以上面案例中的"轴对称的性质"为例,在教材编排的这一阶段,几乎每一节课都会出现这一知识的身影.所以,在这一知识出现时,我们就应将其置于课堂教学的最重要的时段呈现出来,通过核心探究活动的设计与实施,让学生的注意力和学习力聚焦于这一知识.
2.发散性
发散性是主干知识的一个非常重要的特点.主干知识在一个或多个条件之上一般会附着多个类别的结论,一些对后续学习与应用影响很大的结论也隐藏其中.以轴对称为例,我们通过对折产生了轴对称图形,在这个图形中,不仅存在相等的线段、相等的角等结论,还有重合图形的面积相等、周长相等结论,还有线的位置垂直(平行)等结论.如此众多的结论,有些是边缘结论,有些是学生后续学习必备的结论,为了让学生今后的学习与应用可以进行多种选择,我们应让他们知晓这些结论,并学会在后续问题解决中"因需而取".
3.发展性
主干知识一般都是具有发展性的,是可以自然延续并适度拓展的.随着学生知识的不断叠加,技能的不断提升,活动经验的不断积累,他们对主干知识的认知也在不断加深,一些主干知识的地位也会发生相应的变化,呈现阶段性主干的特点.有些知识在初一是主干知识,到了初二有可能变为边缘知识,或者是被新的主干知识所兼容合并.以"线段的中点"为例,在初一上学期,它就是"图形认识初步"的主干知识,是学生用以解决这一单元问题的重要工具;而到了初二,随着学生对"图形与几何"认识的加深,这一知识被逐步兼并融合,其地位被其他主干知识所代替.
4.应用性
主干知识是数学的核心知识,属于数学知识系统中的重要"分子".应用性是这类知识最显著的特点.在学生新知学习和问题解决过程中,主干知识的身影几乎无处不在,其所起到的作用是边缘知识无法代替的.试想,如果没有勾股定理,我们怎样去探究直角三角形的性质;如果没有有理数的运算,我们如何研究整式的运算和解方程;没有一元一次方程,如何探究多元、高次方程……很明显,主干知识正是因为学生获得知识和问题解决的需要而产生的,反之,也正是这些知识所具有的这种应用性,才使之成为学生学习过程中最为重要的主干知识.
三、教学启示
1.提前规划,以发散训练埋下教学伏笔
从上面的特点分析不难看出,主干知识一般都是学以致用的,这就决定了教师教这类知识时应凸显其应用性,学生学这类知识也应以应用为目标.为了发挥主干知识的应用价值,在教学设计与实施过程中,我们不仅要关注这些知识本身的教学,还要重视教学的前后关联,确保后续学习中要用的知识必须学到,而且要学到位.这些知识的获得,会为后续学习形成"生长点",埋下知识学习与应用的伏笔.基于主干知识的发散性和发展性,我们可以通过师生、生生间的对话,将主干知识之上附着的结论尽可能多地有序呈现出来,并从中将与后续教学活动关联最大的结论挑选出来,重点分析,重点强调.这些重要而丰富的数学结论的获得,在学生问题解决时提供了多样的选择,他们会从这些"成团"的结论中筛选出适用的结论应用到问题解决过程之中,以实现自己的学习目标.以本文案例中所说的主干知识为例,在教学"轴对称"和"轴对称图形"时,我们完全可以让学生自己作出一个普通四边形关于某一直线的轴对称图形,然后让他们尽可能多地陈述自己从图形中获得的结论,这样一来,学生的思维就被打开了.作图为他们获得了直观的感知,结论的陈述让他们的思维插上了翅膀,不同的思维角度可能会产生多种不同的结果.在学生全盘呈现结果后,我们可以进行对错辨析,并从中挑选出最重要的也是后面学习及解题要用到的结论,将其在学生的认知网络中"定格".如此一来,主干知识的主体地位得到了充分的保证,同时也为后面教学清除了"障碍".
2.精准衔接,以有效对接凸显主干价值
在教学设计时,我们应该高度重视新旧知识衔接教学的设计.旧知在何时以怎样的形象出现,新知在哪个节点上以什么样的姿态引入,都是教师进行教学设计与教学实施时应关注的.巧妙的衔接是"无痕"的,让学生的知识应用与获得十分的"惬意".这在主干知识的教学与应用中显得尤为重要,作为老师,我们知道主干知识的重要,但我们是不能用过多的言语告知学生"这个知识有多么的重要",更不能在教学过程中让这些知识"强行切入",生搬硬套,让学生"被迫"无奈地感觉新知的获得"非他不行".事实上,有些知识的获得不一定非要主干知识的参与,直观的探究加上其他边缘知识的参与同样可以得到最后的结果.因此,我们常说的"设计有效的教学",应将设计的重点放在知识的关联之上,通过巧妙的符合学生认知规律、紧贴学生实际的问题设计,实现知识间的精准对接,从而凸显出主干知识的价值.看看上面案例中李老师给出的教学过程,我们不得不佩服:自主操作,唤醒的是旧知识和旧经验,在"怀旧"上做文章,从熟悉入手,学得轻松愉快;陈述重合,给出的是新体验和新发现,在"对接"上动脑筋,从结果着眼,获得自然顺畅;抽象归纳,获得的是新知识和新经验,在"出新"上下功夫,从抽象出发,生成有意有效.
3.适时抽象,用新知生成展示应用成果
数学是一门抽象的学科,数学知识的获得一般都应经历抽象的过程,主干知识的学习与应用尤其如此.抽象、模型和推理是初中阶段的三个最重要的数学思想,而抽象是最为常用的,几乎这一阶段出现的所有主干知识都离不开抽象.实用性是初中数学的一个重要特点,因此,很多数学结论的获得都是在一定的生活情境之上的,想要排除这些情境的干扰,让学生获得纯粹的数学知识,除了用纯粹的数学问题代替情境问题,我们还可以通过问题解决过程中的适时抽象来实现.抛开生活情境丰富的实际问题不谈,就以本文中这则案例为代表几何教学为例,看似几何问题数学化程度较高,但离最终的数学规范结论还有着较大的距离.为了让学生避免过多非数学情境的干扰,我们应让学生从图形认识(如本文中的折叠等腰三角形纸片)开始,他们在直观体验过程中,埋下抽象的"种子";当学生从图形的辨析与操作中获得了非数学的结论(如本文中的"重合的图形")时,他们在观察分析中,获得了离数学化结论最近的结论.做好了以上这两步,学生的思维基本上打开了.接下来,就是抽象,从这些丰富的图形中用符号、式子将发现的结论"提取"出来,用获得的旧知以数学的方法加以验证,这样,数学化的结论在师生、生生的思维碰撞中自然生成.通过适时抽象,新知"悄然"生成,充分展示了主干知识的主干价值,让主干知识的应用成果实现了"数学化",为接下来的进一步探究铺平了道路.
