对探索"多边形内角和公式"的思考
2016-09-20安徽省蚌埠市新城实验学校高厚良
安徽省蚌埠市新城实验学校 高厚良
对探索"多边形内角和公式"的思考
2015年11月,笔者有幸在安徽省黄山市观摩了第九届全国初中青年数学教师优秀课展示,来自全国的各路"高手",通过炉火纯青的教学展示、成熟稳定的发挥及智慧娴熟的答辩为观摩老师奉献了一道道丰盛的精神大餐.在观摩的多节展示课中,有两位老师依据自己对教材的理解,通过独特的教学设计、新颖的探究方法、思想方法的不同参透方式,对"多边形内角和"进行了精彩演绎,引起与会众多老师的共鸣.本文拟对两位老师的"多边形内角和公式"探究方案进行展示,并给出解读与思考,与同行研讨.
一、探究方案片断展示
1.R老师的探究方案
问题1:每个小组从准备好的资料盒里取出一张长方形卡纸,任意剪掉一个角,思考有几种不同的剪法,剪出可能的图形.
老师预设有三种情形,如图1、图2、图3所示.
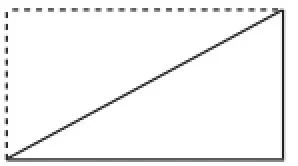
图1
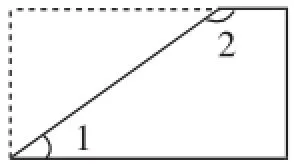
图2
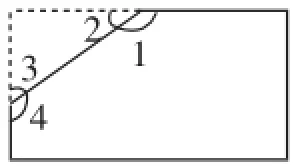
图3
师追问:剪出的图形的内角和是多少度?你是怎么计算的?
(图1、图2得到的三角形、梯形是学生在小学学习过的,很容易知道内角和,但对于图3,裁剪的学生只给出了大概的猜想,认为肯定大于360°,没有严谨的推理说明)
师:对于图3这样一个五边形,内角和应该是多少度呢?请同桌之间相互讨论交流后,写出解答过程.
学生交流后,给出如下两种解决方法:
方法1:利用平角定义及三角形内角和,确定∠1+∠4=270°,进而确定五边形内角和.
方法2:通过∠1或∠4的顶点作垂线,把五边形转化为梯形与长方形计算.
总结:(老师结合方法2)像这样,把新的问题转化为旧的问题,用旧的知识解决新问题的方法,在数学上叫"转化"的数学思想.
问题2:正方形、长方形、平行四边形、梯形等特殊四边形的内角和为360°,对于任意的四边形能否利用"转化"求出内角和呢?请每个同学画出任意一个四边形,利用"转化"的思想把新问题转化为旧知识进行解决.
学生经过4~5分钟的思考交流,小组代表展示了四种转化方法:①连对角线转化为两个三角形;②三角形+特殊四边形;③边上取点转化;④内部取点转化.
问题3:大家通过不同角度的思考,证明了任意四边形的内角和为360°,那么任意五边形、六边形、七边形、…、n边形的内角和又是多少度呢?
(学生通过独立思考后,小组内部再交流各自想法)
学生通过求五边形、六边形,进而总结出n边形的内角和,其中在类比四边形的转化办法求五边形、六边形的内角和时,除出现了过一个顶点作对角线、在一边上取一点、在内部取一点的方法外,还出现了将五边形分成一个四边形和一个三角形,六边形分成两个四边形或一个五边形和一个三角形的奇妙想法.
问题4:同学们刚才通过从顶点出发、从边出发、内部取一点的方法研究了四边形的内角和,若从外部任取一点又能否通过转化得出结论呢?
(因时间关系,留到了课下研究)
2.C老师的探究方案
问题1:三角形内角和是多少度?正方形内角和是多少度?长方形内角和是多少度?对于资料盒中的任意四边形纸片内角和是多少度?猜猜看,你能验证吗?
学生有用量角器测量,有用纸片进行撕拼、折叠等,老师在学生有了想法后,让学生讲解自己的思路.
问题2:(老师在黑板上放个四边形纸片,形成一个任意四边形,如图4)对于黑板上的四边形还可以折叠吗?这个图形该怎样求它的内角和呢?
图4
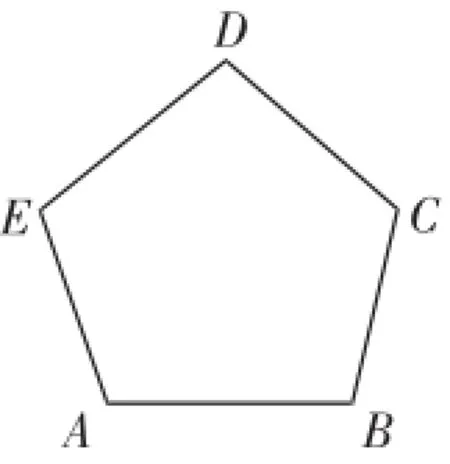
图5
在学生讲述通过折叠想到连接对角线,把四边形转化为两个三角形解决后,老师让学生把解决过程用几何推理的方式写在学案上.
问题3:(老师从讲台上拿一个五边形纸片,在黑板上形成一个任意五边形图形)如图5,对于这样一个五边形,你也能得到它的内角和吗?请同学们思考一下.
问题4:能否用类似的方法求出六边形、七边形、…、n边形的内角和呢?请同学们小组讨论后再填写下面的表格:
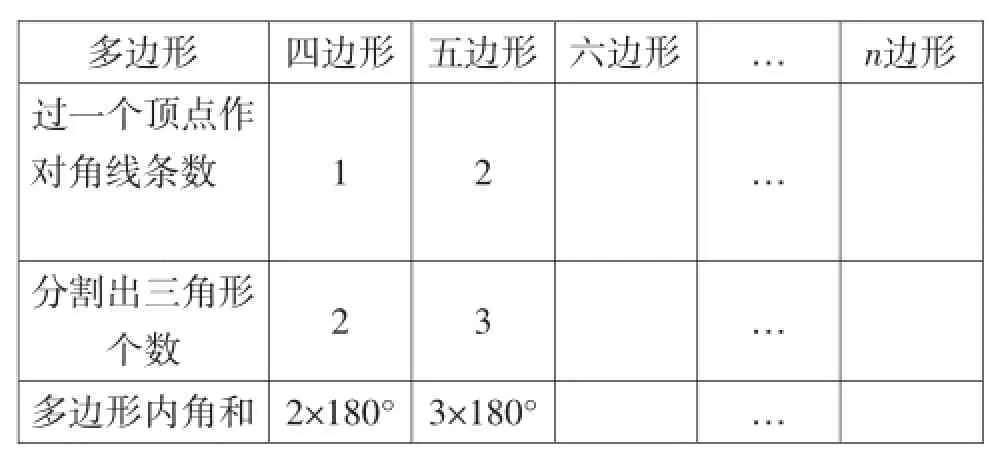
多边形四边形五边形六边形…n边形过一个顶点作对角线条数1 2…分割出三角形个数2 3…多边形内角和2X180° 3X180°…
问题5:对于任意五边形,除了刚才的分割方法,你还有没有其他的分割方法呢?请思考后,小组内交流想法.
学生经过讨论交流后,得到如下分割方法:①边上取点与其他各点相连;②三角形+四边形;③内部取点后与其他各点相;④外部取点后与其他各点相连.
问题6:(学生分享各种分割方法后)这些分割方法有什么相同的地方?
生:都是通过分割的方法将五边形分成两个三角形,或一个三角形与一个四边形.
师:这其实是一种转化思想,即把未知的问题转化为已知的问题来解决.(最后用几何画板演示通过点的移动得到五边形分割的各种方法)
二、两个方案片断的解读
1.对R老师探究方案的解读
R老师对多边形内角和公式的探索总体上采用了由特殊到一般,由具体到抽象的教学策略.一方面通过学生自主思考与互动研讨,把问题的研究从特殊引向一般,让学生充分经历探索多边形内角和的全过程;另一方面在定理的推导过程中,注意分析如三角形、特殊四边形等已有模型的特征,通过已有的模型研究、转化、类比.在具体的探究上,R老师采用开放式的探究教学模式,如在任意四边形、五边形、六边形、…、n边形内角和探索方案上突出开放性问题的设计与提出,启发学生从不同方面思考问题、解决问题.开放性问题由于没有指明研究的方法,只提供研究的方向,为学生的自主探究留足了空间,开放性问题的提出,激发了学生探究的兴趣,使学生的思维始终停留在一个高层次的活动中,一个个精彩的探究方案便自然地呈现了出来.难能可贵的是,学生竟然想到把五边形分成一个三角形和一个四边形,六边形分成一个三角形和一个五边形或两个四边形的探究方案,笔者想没有R老师的开放性探究策略,留给学生充分自由的探究时间,是不可能出现这种难能可贵的原生态的思维过程的,也更不可能出现那位女同学"转化是不需要任何形式与套路"的精彩总结.
2.对C老师探究方案的解读
C老师对多边形内角和的探究方案可复制、可翻讲、接地气,家常便饭但又与众不同,
过一点作对角线是C老师探究方案的主线.首先通过四边形纸片折叠的方式确定内角和,过渡到当一个任意四边形、五边形不能折叠时,该如何确定它的内角和,让学生经历分割的方法将四边形、五边形内角和问题转化为三角形内角和问题,初步感受转化与化归的数学思想,再通过学生完成表格的形式确定n边形内角和,使学生形成一条完整的思维链.整个过程,过渡自然,逻辑连贯,一气呵成.为了让学生更好地体会"转化、化归"的数学思想,C老师又通过让学生用其他方法探究五边形内角和,最后让学生思考这些方法的共同点后,C老师才道出点睛之笔(转化、化归的数学思想).在一些细节的处理上,如通过把纸片放到黑板上,形成几何图形,对几何推理的重视及通过几何画板演示让学生体会分割五边形各种方法的共性等,都让人眼前一亮.
三、对探究多边形内角和相关问题的思考
1.对"特殊到一般"探究方式的思考
对于多边形内角和公式的探究,虽然老师们采用的具体方式有所不同,但基本上都是遵循由特殊到一般的探究策略,即通过特殊四边形的内角和过渡到任意四边形,进而推广到五边形、六边形,……最后推导出n边形内角和公式.但对于任意四边形内角和的探究上,虽然方案各异,但本质上都是在平面内取一点与四边形各点相连,这一关键点的选择是否也可以采用由特殊到一般的探究方案呢?即通过在四边形所在平面内首先找一个特殊点(如两条对角线的交点)与各顶点相连进行探究后,再通过点的移动确定相应的方案.这是否在渗透转化、化归思想的同时,更有利于学生理解不同探究方案的本质呢?我们在惊叹R老师的学生发现那么多探究方案的同时,也在遗憾为什么就没有学生通过延长四边形的两边构造三角形这种情况,这是否与老师在这方面的引导的欠缺有关呢?
2.对"问题趋动"教学的思考
我们知道,数学问题的提出是驱动整个数学课堂教学的关键,在平时的教学中,老师们都遇到过这样一种情况,当把问题抛下后,有时候老师费了九牛二虎之力,学生仍是启而不发,一般认为主要原因是问题的设置起点过高,难度较大,超出学生的能力范围.通过本次观摩,笔者认为除了以上原因,还有一个很大的原因是老师开始所提出的问题能否驱动整节课教学的开展,二位老师展示课中问题的设置就让人眼前一亮.R老师通过一个开放性的问题:一张长方形卡纸,任意剪掉一个角,思考有几种不同的剪法,这个问题起点很低,学生参与进去很容易,但要想完整解决这个问题,又需要分类讨论,更为可贵的是,这个问题起到了驱动整个课堂教学的目的,即先解决特殊的四边形、五边形(如对边平行的或含有直角的),再解决一般的四边形,进而解决一般的n边形;而C老师通过任意四边形纸片内角和是多少度的一个简单问题,通过学生的折叠,由折痕联想到添加对角形,而过一点作对角线是C老师探究n边形内角和的主线.
3.对探究方案的思考
在多边形内角和的探究上,传统上采用的方法都是把一个多边形利用转化的方法变成三角形相关问题解决.那我们能否另辟蹊径,反其道而行之,以内角的增多而引起内角和的变化来研究多边形内角和问题呢?如图6,如何由三角形的分割而得到四边形,由四边形分割得五边形,进而得出n边形内角和呢?或者如图7,在三角形外增加一个三角形得四边形,四边形外增加一个三角形得五边形,…,利用这种"递推"的方法,与传统的方法相比哪一个更自然,哪一个更利于学生探究活动的展开,也是我们不得不思考的一个问题.再比如,在多边形内角和与外角和的探究顺序上,可否考虑先研究多边形的外角和,再利用内外角的关系研究内角和呢?有兴趣的读者不妨试一试.
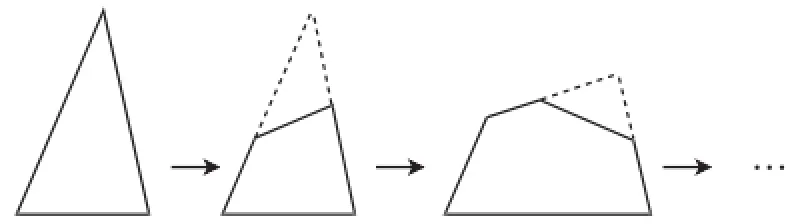
图6
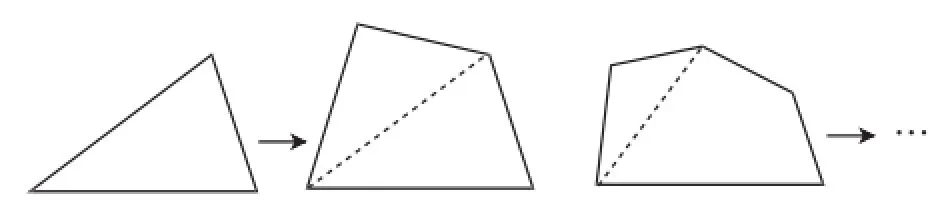
图7
4.适合教与学的方案才是最好的
对于教材某个教学环节的不同处理,很多老师都会思考,哪一种方法更好,哪一种方法更能体现出老师的"功夫"?这或许有利于老师通过反思优化自己的教与学生的学.然而,世界上没有两片完全相同的树叶,不同的老师面对的学生都是独特的"这一个",他们在整体成绩、思维发展的水平、主动探究的意识都存在着差异,作为主导者的老师在个人的教学水平、调控课堂的能力、个人魅力等方面也不尽相同.老师只能尊重和理解学生,针对学生的差异和发展需求,寻求适合自己及班级学生实际情况的方法.比如,对多边形内角和的探索,若班级内学生思维活跃、乐于探究,自己的调控能力不弱的话,不妨就通过开放性问题,给学生足够的时间去探索,让学生的思想真正解放(如R老师方案);若班级内学生水平一般,学生的思维有所欠缺,老师给学生一个探究"暗示",也不失为一种突破难点的好方法.被别人用实践证明的好方案,却不一定适合自己的教学,简单的"复制",效果并不一定好.再比如,在数学思想的渗透上,在评课环节,很多老师认为R老师过份强调了"转化"的数学思想,认为数学思想应让学生去体会,老师不应说出来,可是笔者觉得,如果平时就注重数学思想的渗透,学生已较多地经历了"转化"的方法解决问题,那这节课着重强调一下也未尝不可,学生在课堂上精彩的表现,不就说明了R老师对数学思想处理的成功吗?所以利于学生思维训练,利于学生的探究,利于自己教学开展的方案就是最好的,简言之,适合的就是最好的.
参考方献:
1.高厚良."意外惊喜"源于以生为本的方案设计---"多边形内角和"的探索方案片段[J].中学数学(下),2013(8).
2.刘华.追求逻辑连贯的数学教学---以"多边形内角和"教学为例[J].中学数学(下),2015(3).
3.沈骏.同课异构:探索多边形内角和的教学品酌[J].教育科学论坛,2010(8).
猜你喜欢
杂志排行
中学数学杂志的其它文章
- "二次根式的运算(第1课时)"课例分析
- 数学课堂中的"技"、"艺"、"道"*
- ---以"平面直角坐标系"省优质课为例">反"逼"的课堂更精彩*
---以"平面直角坐标系"省优质课为例 - 注重类比迁移,渗透研究套路
---以七年级"角(第1课时)"教学为例 - 生活问题数学化数学角度看世界
---以"篮球运动中的数学问题"为例 - 概念教学:积跬步以至千里*
