冷弯厚壁钢管短柱试验及规范公式比较

温东辉， 沈祖炎， 李元齐， 朱少文

(1. 同济大学 土木工程学院，上海 200092；2. 太原学院 建筑工程系，山西 太原 030032；3. 同济大学 土木工程防灾国家重点实验室，上海 200092；4. 武钢集团汉口轧钢厂，湖北 武汉 430035)



冷弯厚壁钢管短柱试验及规范公式比较

温东辉1,2， 沈祖炎1,3， 李元齐1,3， 朱少文4

(1. 同济大学 土木工程学院，上海 200092；2. 太原学院 建筑工程系，山西 太原 030032；3. 同济大学 土木工程防灾国家重点实验室，上海 200092；4. 武钢集团汉口轧钢厂，湖北 武汉 430035)

以宽厚比为主要变化参数，进行了16根冷弯厚壁钢管轴压短柱试验，研究冷弯效应对强度的影响.试验结果表明：荷载-位移曲线的形状主要取决于截面的宽厚比.宽厚比较小时，达到峰值荷载后下降较慢，邻近破坏时构件的轴向位移很大；宽厚比大时，局部屈曲影响明显，荷载达峰值后下降较快.同时基于试验结果，与国内外规范考虑冷弯效应的屈服强度计算公式进行了比较，认为我国规范考虑冷弯效应的屈服强度计算公式对于全截面有效的冷弯厚壁型钢也是适用的，且偏于保守.

冷弯厚壁钢管； 短柱试验； 冷弯效应； 规范公式； 宽厚比

与热轧型钢相比，在建筑结构中采用冷弯型钢具有诸多优点：由于采用冷加工成型工艺，型钢壁板的宽厚比较大，而不像热轧型钢那样受到限制，且断面形状灵活，单位质量的断面性能较热轧型钢优越，因而截面高效，可节省钢材约10%～40%；冷轧成型钢精度高、速度快、产量高，且不损伤涂层，适宜大批量工业化生产.同时，冷弯型钢结构也具有一般钢结构力学性能好、抗震性能优越、可有效降低建筑物自重、连接方便、施工迅速、环保、材料可循环利用等优点[1-2].

目前，国内外对冷弯薄壁型钢基本构件静力性能的研究主要集中在冷弯薄壁铝合金[3]、薄壁不锈钢[4]及高强超薄壁型钢[5-6]等方面.对冷弯厚壁钢管轴压构件的研究[7]也多属于长柱，对短柱的系统研究比较少.短柱试验可以反映冷弯效应的水平对强度的影响，既能确定整个截面的平均屈服强度和应力应变关系，又可以反映残余应力对压杆力学性能的影响.因此，本文对冷弯厚壁钢管典型截面进行了短柱试验研究，共16个试件.基于试验结果，并结合已经完成的材性试验，与国内外相关规范考虑冷弯效应的屈服强度公式进行比较，提出了建议，可为相关规范修订提供参考.

1　试验概况

1.1试件设计

以宽厚比为主要因素，设计了16根方、矩形钢管轴压短柱构件.试件长度的选取应避免发生整体屈曲，因此不能太长；另一方面，短柱也应该足够长以保证沿构件各截面具有均匀的应力分布，减小端部过大的约束效应对试验结果的影响.本文短柱长度取3倍的截面长边尺寸，16个试件的截面规格等信息详见表1.表中试件编号说明：顺序号-重复试件代号-钢材等级-截面类型-长边尺寸-壁厚.其中，A，B，C指相同试件重复号；Q1，Q2分别表示Q235，Q345；截面类型S，R分别表示方管和矩形管.

表1　短柱试件截面及编号

1.2试验加载与测量装置

短柱试验在浙江大学结构试验室10 000 kN微机控制电液伺服多功能试验机上进行.试验时，构件上端的附加端板与试验机加载头端板用高强度螺栓连接，构件下端板与底座用锚栓相连，装配好的试件实物图见图1.

为得到短柱受压过程的荷载-位移曲线，采用百分表和电子位移计记录短柱竖向位移.位移计和百分表分别布置在短柱的4个角部和各个面的中部.在短柱高度中央部位，沿截面对称布置应变片，如图2所示.具体为：在平板中间位置各布置1片(边长大于300 mm的面布置2片)，同时在弯角中心部位各布置1片，截面上的应变片总数为8～12片.应变片在试验初始阶段起对中作用，在试验过程中也可以根据应变曲线判断截面的实际受力状态.

a上下端板b试验加载全景

图1　短柱加载装置

图2应变片沿截面的布置

Fig.2Location of strain gauges along sections

2　试验结果及分析

2.1破坏形态

短柱试验在峰值点处的破坏形式主要分为两类：一类是全截面材料屈服的强度破坏；另一类接近峰值荷载时截面上部分区域材料开始屈服但未达到全截面屈服时板件开始屈曲，发生局部失稳破坏.各试件在峰值点处的破坏模式除试件8，9，10，18，30，31为局部失稳破坏外，其余试件均为强度破坏.

图3给出了试件的最终变形模式，通过分析可以发现有如下规律：试件的最终变形模式根据宽厚比可分成三类.第一类属于材料全截面屈服，大部分试件在靠近钢管上端或者下端发生四周外鼓，个别试件三面外鼓，一面内凹；第二类属于局部屈曲变形，这类试件沿高度不同位置发生局部屈曲变形，即对边内凹和邻边外鼓的现象；第三类属于整体失稳和局部失稳同时发生的情况，整体失稳导致跨中发生侧移，宽厚比较大的矩形截面多发生此类破坏.各试件的峰值点处破坏及最终变形模式详见文献[2].

2.2荷载-位移曲线

图4和图5给出部分试件的荷载-位移曲线.可以看出，荷载-位移曲线的形状主要取决于截面的宽厚比.宽厚比小时，达到峰值荷载后下降较慢，邻近破坏时构件的轴向位移很大；宽厚比大时，局部屈曲影响明显，荷载达峰值后下降较快.

a 第一类

b 第二类

c 第三类

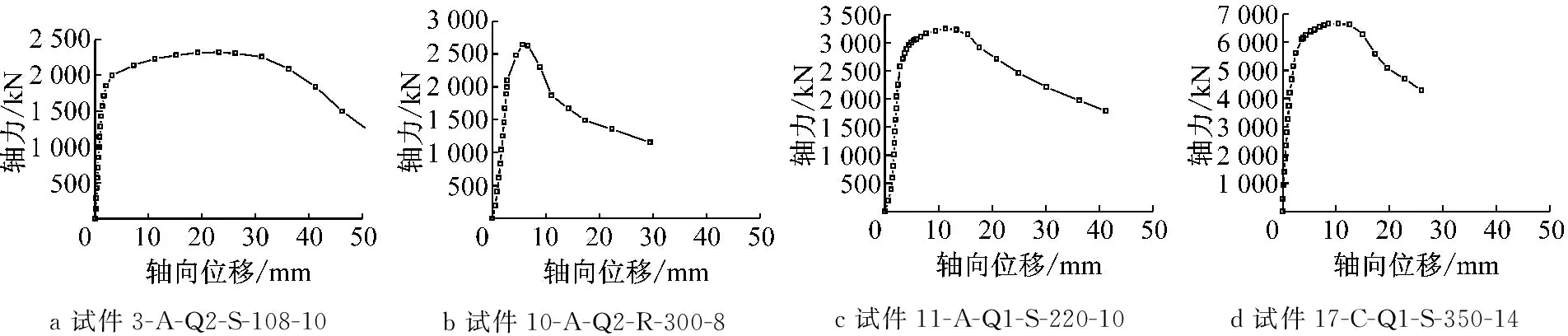
a试件3-A-Q2-S-108-10b试件10-A-Q2-R-300-8c试件11-A-Q1-S-220-10d试件17-C-Q1-S-350-14

图4　宝钢典型短柱荷载-位移曲线

图5武钢典型短柱荷载-位移曲线

Fig.5Typical stub column load-displacement curves of WISCO production

对同一截面的重复试件比较见图6，由试验结果可知，对宽厚比较大的试件，初始缺陷的影响较大，如截面250 mm×250 mm×8 mm的实测宽厚比达33.24，两根重复试件的荷载有明显差异；而对小宽厚比试件，如截面108 mm×108 mm×10 mm，荷载-位移曲线仅在试验接近结束时有分叉，破坏前性能稳定.

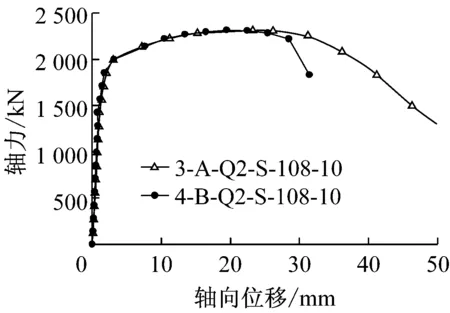
a 截面108×108×10(Q345)

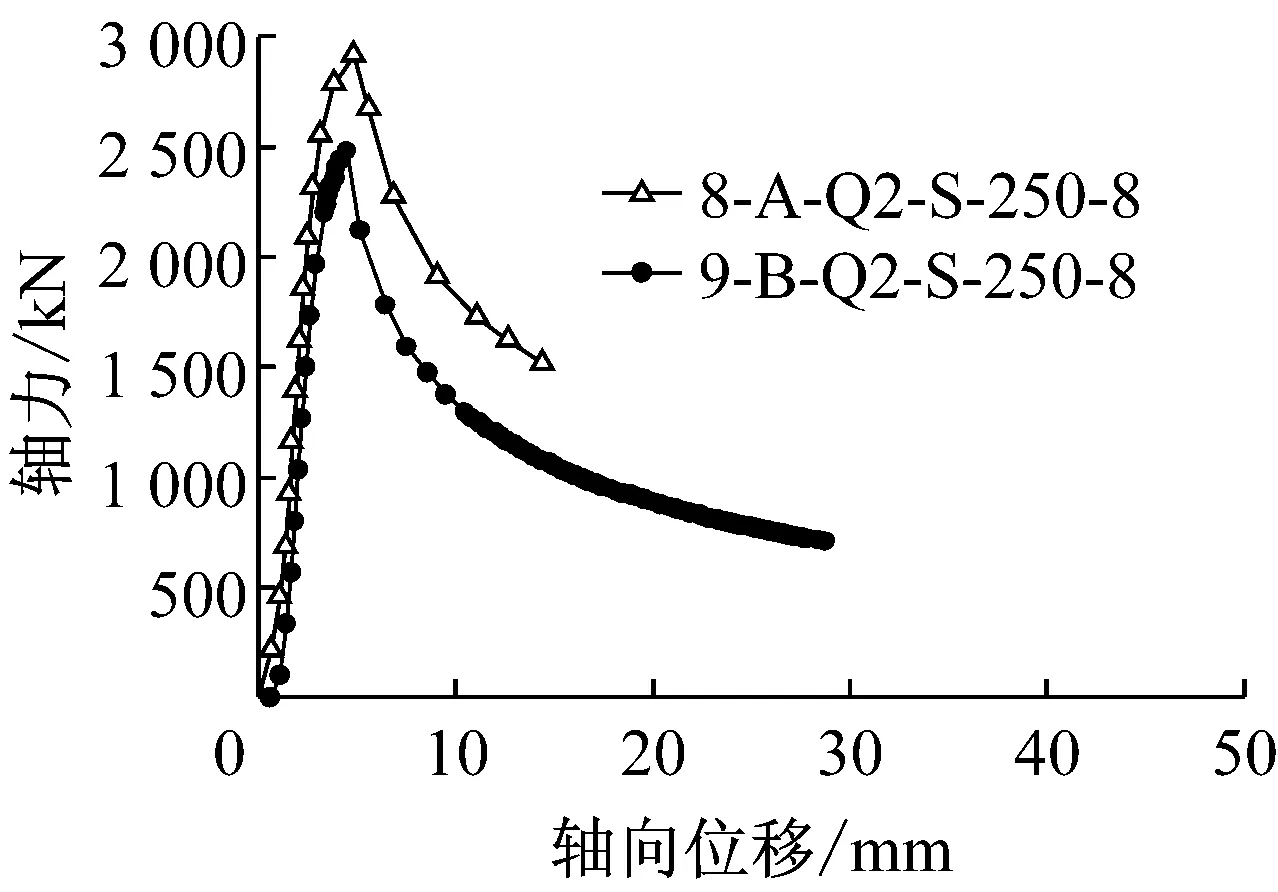
b 截面250×250×8(Q345)

Fig.6Comparison of stub column load-displacement curves from same sections

2.3应力-应变结果

图7给出了采用位移计得到的平均应变和用应变片得到的应变结果.试验发现，对大部分试件，二者吻合较好；对个别试件，由于试件端部不平整等原因，二者略有差异.

表2给出了各个短柱试件的屈服应力fy,stub和极限应力fu,stub.其中，屈服应力采用的是0.2%应变对应的应力[9].

3　考虑冷弯效应的冷弯厚壁型钢的强度计算公式

3.1短柱试验结果与采用钢管截面屈服强度分布模型计算结果的对比

3.1.1采用屈服强度分布模型的计算

图8是钢管截面屈服强度的分布模型[10].图中，B和H分别为钢管截面的宽和高；r为弯角的内径，r=1.2t；R为外径；t为管壁厚度.F表示平板，C表示弯角，W表示焊缝部位.fy为两邻边(指与焊缝边相邻的两边，下同)的屈服强度，fy前的数字为钢管冷成型后屈服强度较fy的提高系数，两邻边fy也应较原材料的屈服强度有所变化.该模型对于Q235钢，邻边fy较原材料的提高值取1.095 8；对于Q345钢，邻边fy取与原材料相同的值.

按此屈服强度分布模型，可按下式计算整个截面的平均屈服强度fy,mod

fy,mod=(1.39AW+1.42AC+Aa+

1.08Ao+An)fy/A

(1)

式中：fy为邻边平板的屈服强度；fy=αfy,0(对Q235，α=1.098；对Q345，α=1.0)；fy，0为原材料的屈服强度；fy，235，fy，345分别为Q235钢和Q345钢的屈服强度；AW为焊缝部位的面积，AW=20t；AC为4个转角部位的面积，AC=18.681 4t2；Aa为两个邻边平板部位的面积，Aa=2(H-6.4t)t；Ao为焊缝对边平板部位的面积，Ao=(B-6.4t)t；An为焊缝边的平板部位的面积，An=Ao-20t；t为钢管壁厚；A为钢管截面面积.

a 试件3-A-Q2-S-108-10

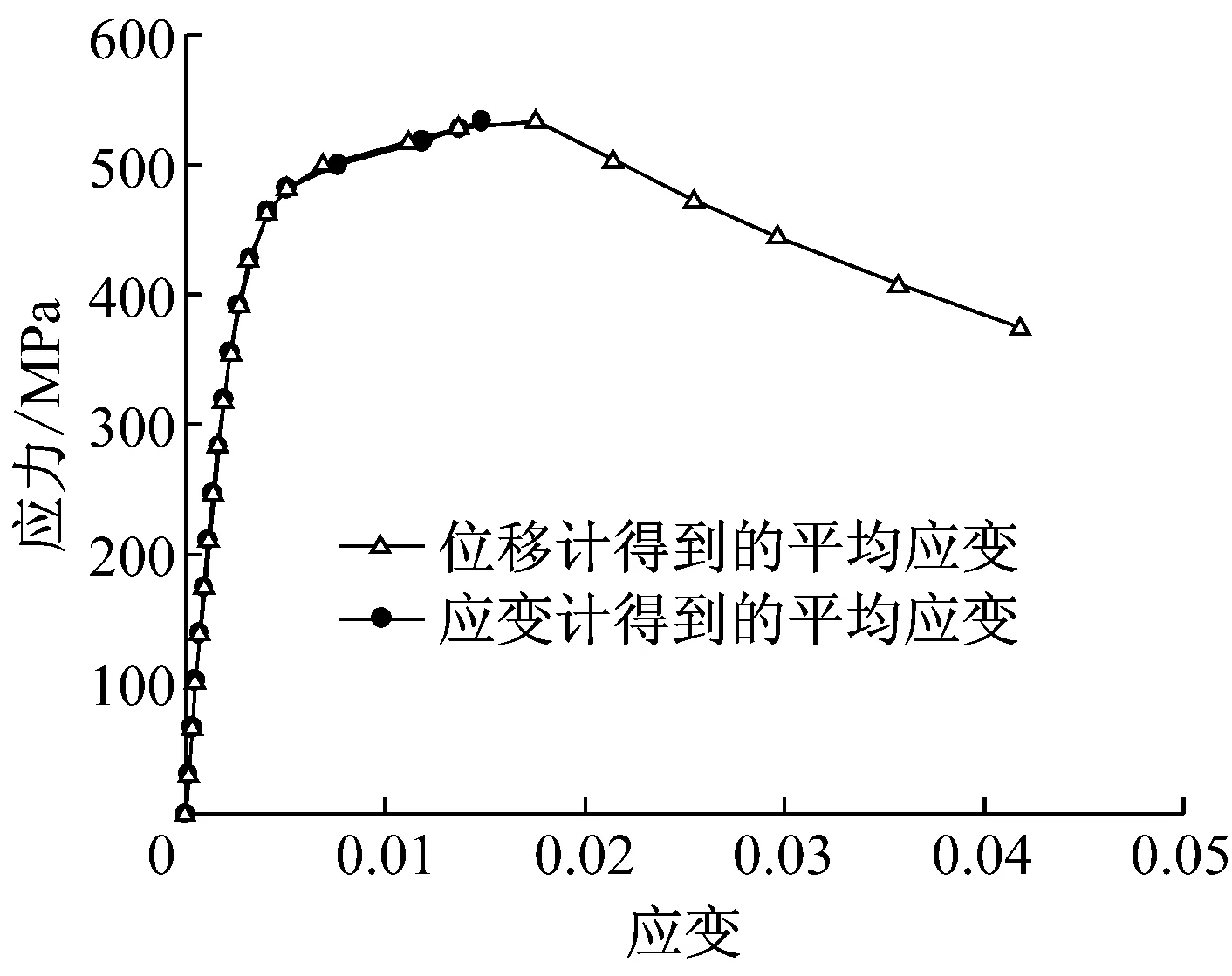
b 试件26-A-Q2-R-160-8

c 11-A-Q1-S-220-10

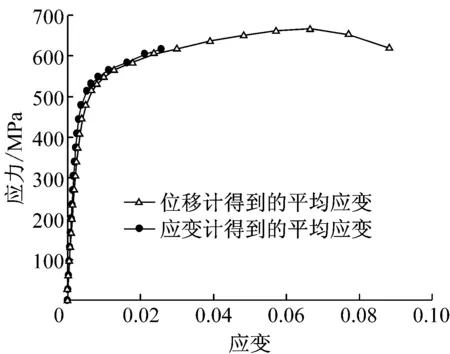
d 24-A-Q2-S-86-8

Fig.7Comparison of stub column stress-strain curves obtained by strain gauges and displacement transducers

表2　短柱屈服应力和极限应力结果

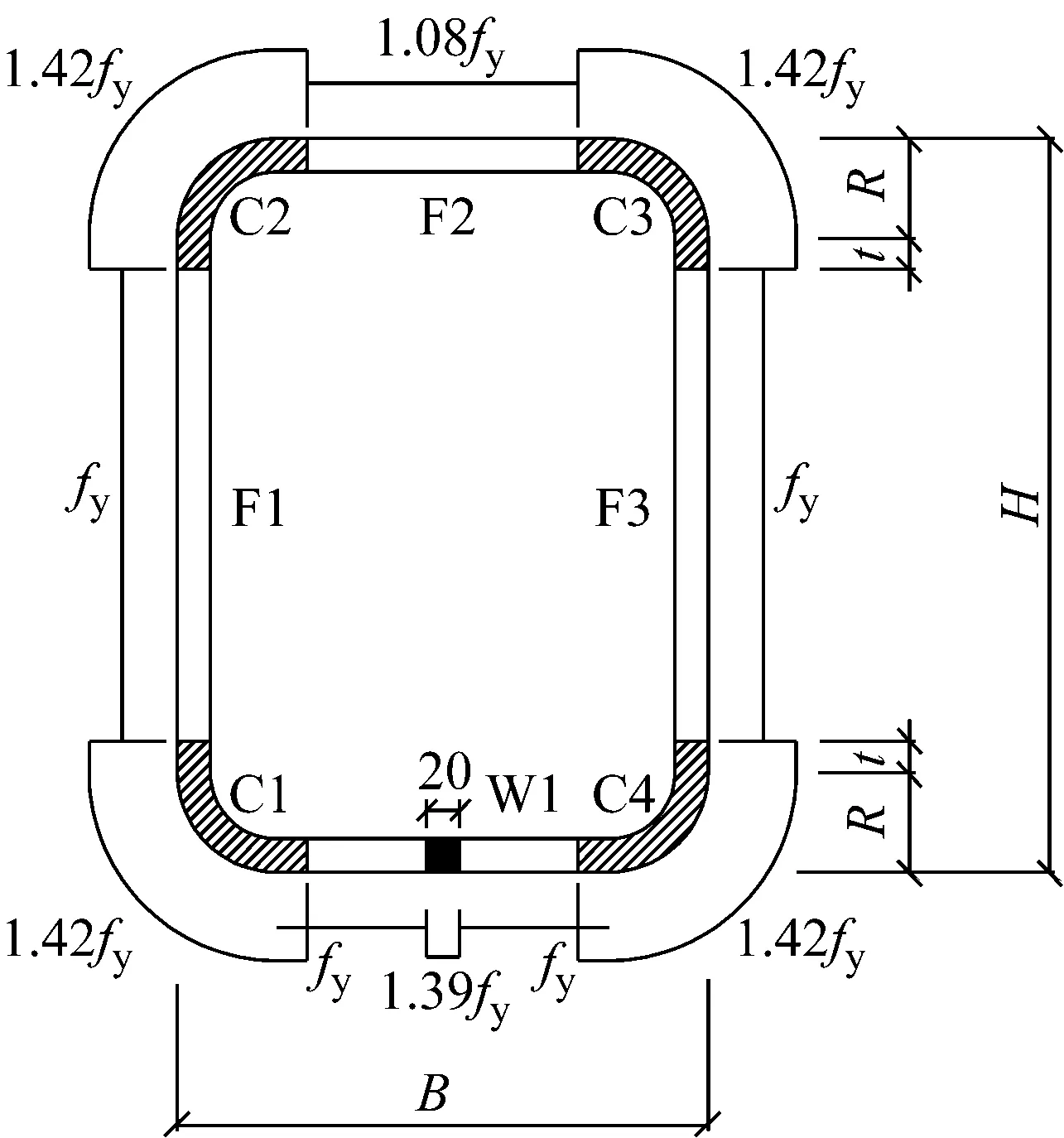
图8　钢管截面屈服强度分布模型

Fig.8Yield stress distribution model for rectangular steel hollow sections

因此采用屈服强度分布模型的整个截面冷弯效应系数βmod可按下式计算：

(2)

3.1.2采用短柱截面各部分实测屈服强度的计算

由于在进行短柱试验时，同时也对短柱截面进行了材料性能试验，因此每一个短柱试件截面的各个部位的屈服强度等材料性能都有实测值[10].利用这些实测值也可按下式计算整个截面的平均屈服强度fy,mat：

(3)

式中：fy,W为焊缝部位的实测屈服强度；fy,C为弯角部位的实测屈服强度；fy,o为焊缝对边平板的实测屈服强度，可取fy,o=fy；fy,n为焊缝边的平板部位的实测屈服强度，可取fy,n=fy.

将fy,mat除以原材料的屈服强度fy,0即可得整个截面的冷弯效应系数βmat.由于无法得到与短柱试件相对应的原材料的屈服强度，此处援用式(2)给出的关系.这样，可得βmat的计算公式如下：

(4)

3.1.3采用短柱试验整个截面实测屈服强度计算

采用短柱试验的整个截面实测屈服强度计算时，整个截面的冷弯效应系数βexp可按下式计算:

(5)

式中：βi,exp为序号i的短柱试件的整个截面的冷弯效应系数；fi，stub为序号i的短柱试件的整个截面实测屈服强度，其值可由表2查得；fi，y为序号i的短柱试件截面中邻边平板的实测屈服强度，其值可由文献[10]查得.

表3列出了各短柱试件按式(5)计算得到的βexp，用短柱截面各部位实测得到的屈服强度值按式(4)计算得到的βmat，用屈服强度分布模型按式(2)计算得到的βmod以及我国规范《冷弯薄壁型钢结构技术

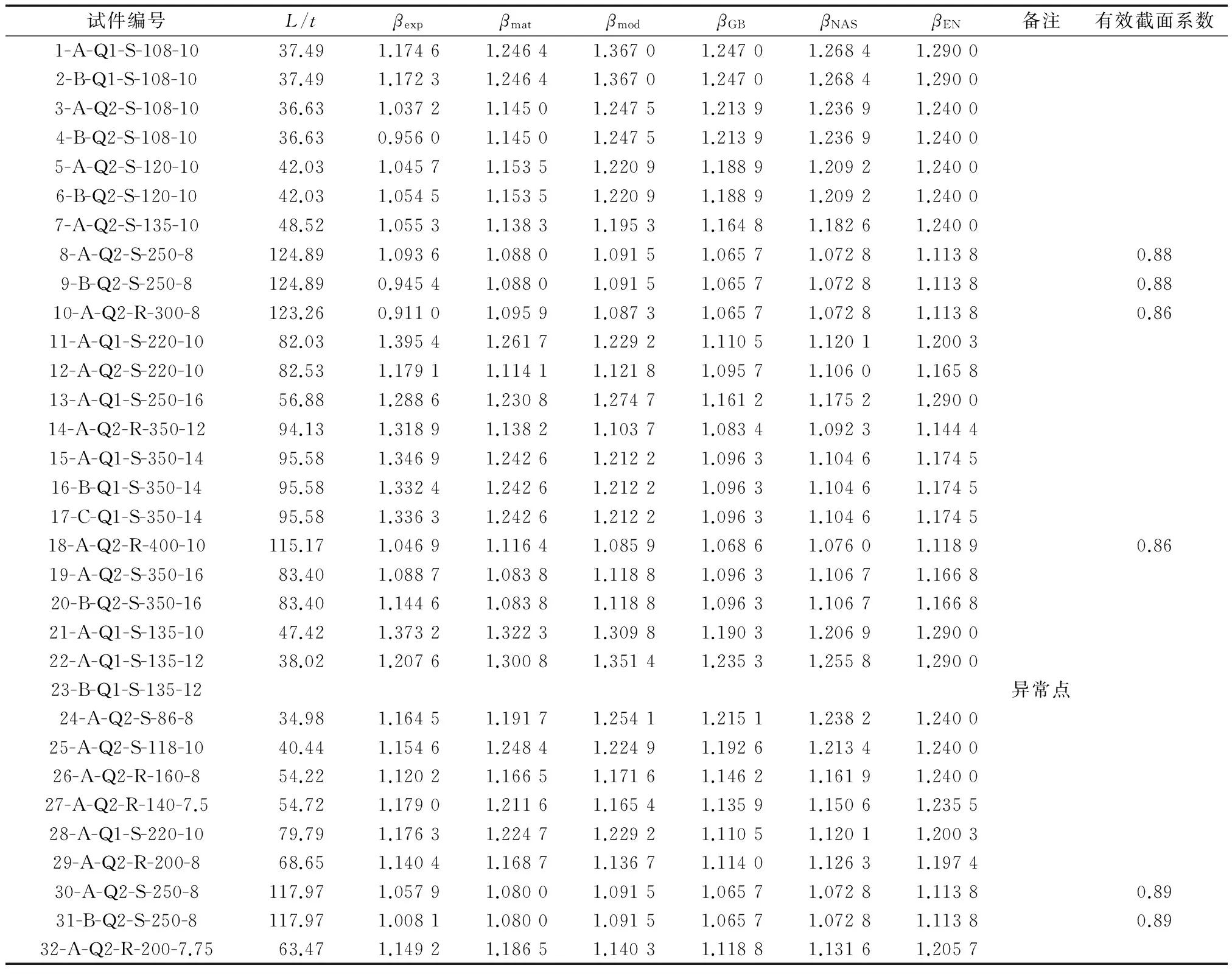
表3　短柱及各国规范冷弯效应提高系数

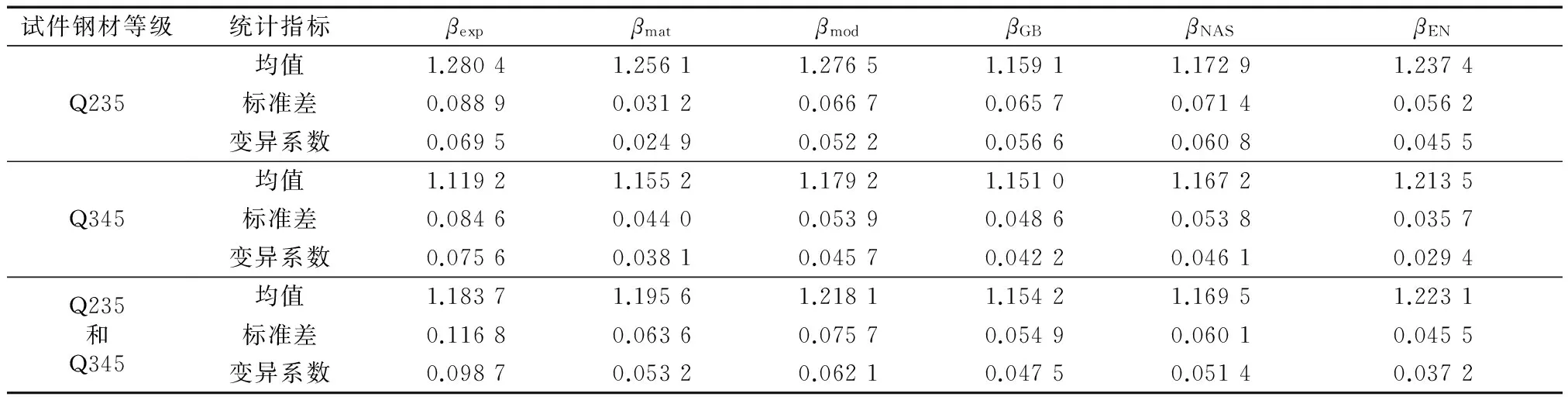
表4　各国规范冷弯效应提高系数统计值

从表3,4中可以看出对25根短柱试件采用三种不同计算方法得到的冷弯效应系数几乎是一致的，对于Q235钢，其平均值之比βexp∶βmat∶βmod=1∶0.981 0∶0.997 0；对于Q345钢，则为1∶1.032 2∶1.052 6.对于每根短柱试件而言，由于βmat计算时所用的材性数据均来自于βexp短柱同一类的钢管截面，因此两者的数值均比较接近，一般均不超过10%.由此也可以说明所建议的屈服强度分布模型的部位划分是可行的.另外，对于每一根短柱试件，由于βmod计算时所用的材性数据均没有取相应的实测值，采用的是平均值，因此两者数值比较的差值在βmat与βexp的比较值上下波动，但βmod与βexp比值的平均值的误差极小，对于Q235钢为0.997 0，对于Q345钢为1.053 6.这也进一步说明屈服强度分布模型可以用来计算整个截面的冷弯效应系数.

3.2国内外规范考虑冷弯效应的强度计算公式

3.2.1我国规范

(6)

式中：f′为考虑冷弯效应的强度设计值；η为成型方式系数，对于冷弯高频焊(圆变)方、矩形管取1.7,对于圆管和其他方式成型的方、矩形管及开口型钢取1.0；γ为钢材的抗拉强度与屈服强度的比值，对于Q235钢可取1.58，对Q345钢可取1.48；n为型钢截面所含棱角数目；θi为型钢截面上第i个棱角所对应的圆周角，以弧度为单位；l为型钢截面中心线的长度，可取型钢截面积与其厚度的比值；f为原材料的强度设计值.

3.2.2北美、澳洲/新西兰规范

北美、澳洲/新西兰冷弯型钢设计规范[12-13]中，考虑冷弯效应全截面平均屈服强度公式为

(7)

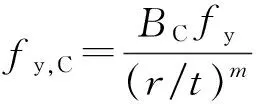
3.2.3欧洲规范

欧洲规范[14]考虑冷弯效应的平均屈服强度公式为

(8)

式中：A为毛截面面积；k为成型方式系数，冷轧成型方式k=7，其他成型方式k=5；n为截面上内半径r≤5t的90°弯角的数值(不足90°的弯角可按具体数值累加).

表3还分别给出了运用我国规范、北美AISI、澳洲/新西兰AS/NZS规范和欧洲ER3规范中考虑冷弯效应的屈服强度计算公式计算得到短柱试件全截面屈服强度，并根据母材的屈服强度进行量纲一化，得到各规范的冷弯效应提高系数，用βGB，βNAS和βEN表示.公式中母材的屈服强度采用名义值，即Q235取235MPa，Q345取345MPa；强屈比对Q235和Q345钢材分别取1.58和1.48.

从表3的βGB，βNAS和βEN值可以看出除个别试件之外，三者相差一般都在7%左右，平均值的差别也小于7%，说明三个国家规范的计算结果差别不大.

3.3各国规范计算值与本文试验结果比较

表5给出了各试件由短柱试验得到的冷弯效应系数βexp和屈服强度分布模式得到的冷弯效应系数βmod与中国规范、北美规范和欧洲规范计算得到的冷弯效应系数βGB，βNAS和βEN间的比值，表6按试件钢材等级给出了其相应的统计值.从表5、表6可以看出，各国规范之间相差不大.对于Q235钢，中国规范略为安全些.对于Q345钢，中国规范最接近试验结果.从与βmod比较的结果可以看出，βmod与各国规范的比值均比较均匀，变异系数都十分小.因此，在建立冷弯厚壁方形和矩形钢管的精确计算模型时，截面上屈服强度的分布可采用本文建议的式(1)所给出的分布模式.

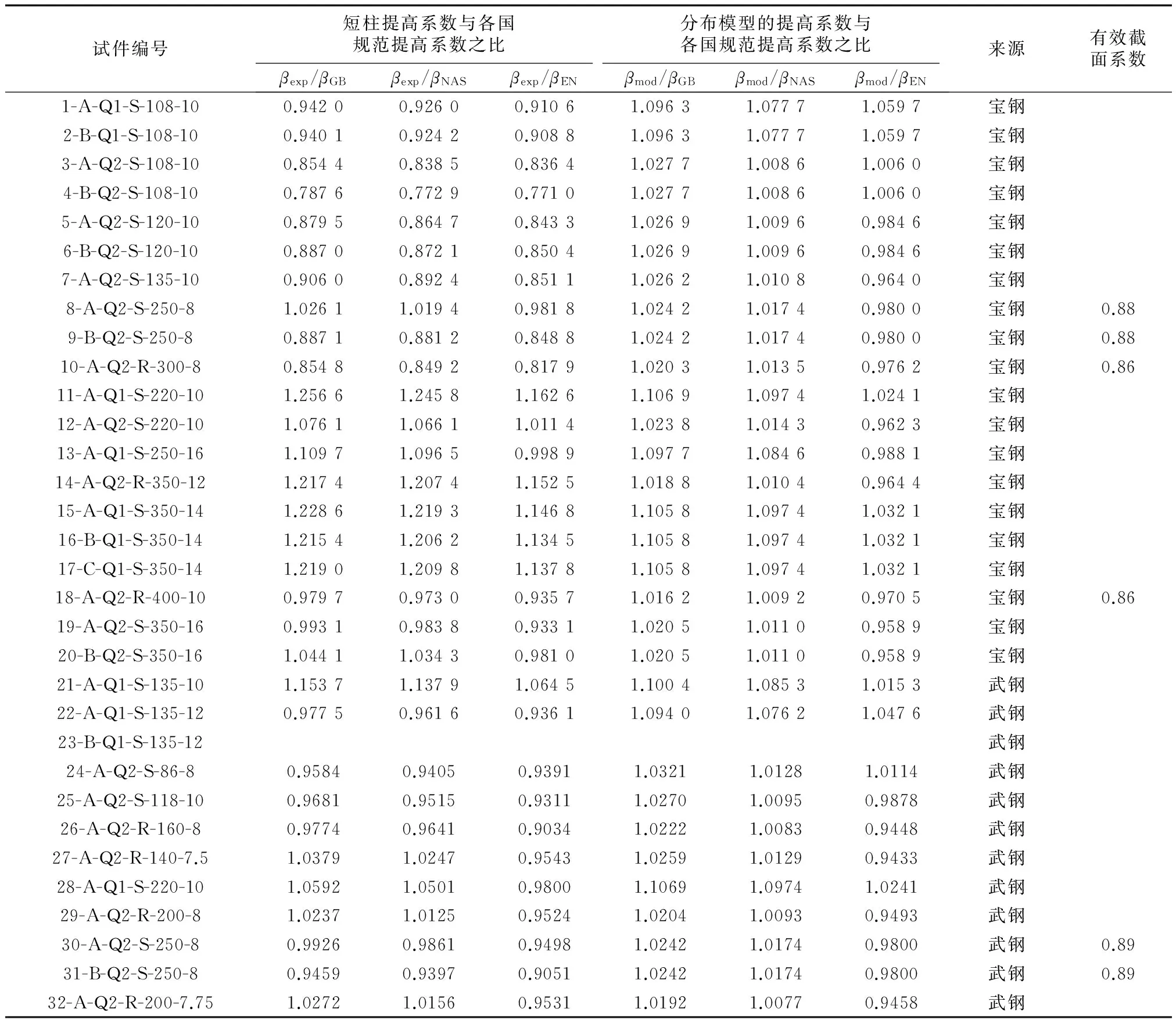
表5　短柱及各国规范冷弯效应提高系数之比

4　结论

(1)宽厚比是决定试件破坏模式的主要因素.短柱在峰值点处的破坏形式主要分为全截面材料屈服的强度破坏和局部失稳破坏两类.试件的最终变形模式根据宽厚比可分成材料全截面屈服、局部屈曲及整体失稳和局部失稳同时发生三类变形模式.

(2)荷载-位移曲线的形状也主要取决于截面的宽厚比.宽厚比小时，达到峰值荷载后下降较慢，邻近破坏时构件的轴向位移很大；宽厚比大时，局部屈曲影响明显，荷载达峰值后下降较快.

(3)本文提出的考虑冷弯效应后的截面屈服强度分布模型，可在建立冷弯厚壁方形和矩形钢管的精确计算模型中采用.

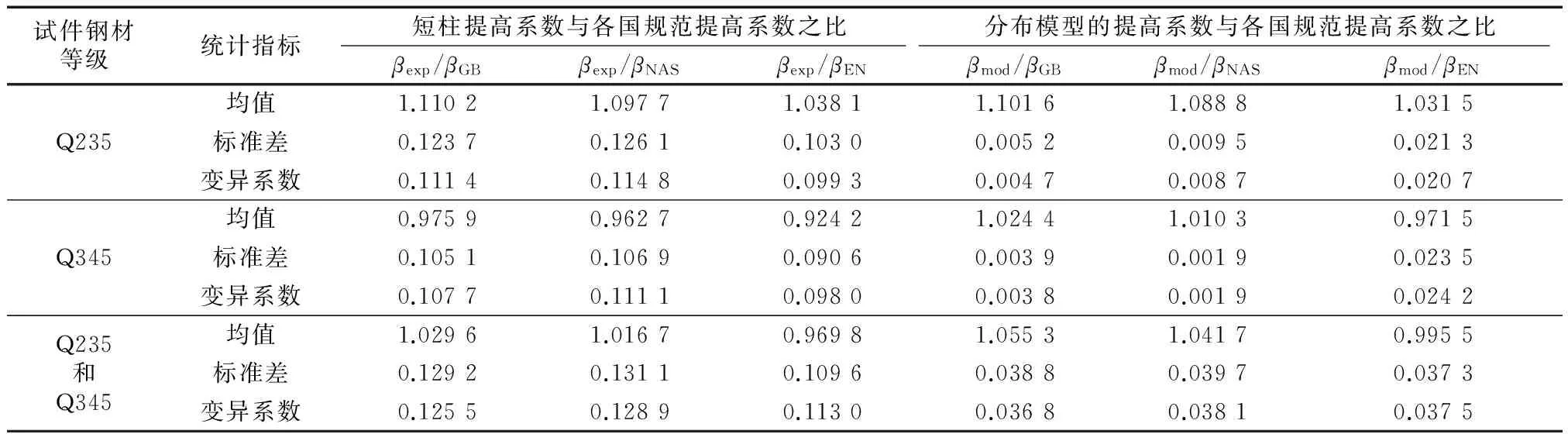
表6　各国规范冷弯效应提高系数之比统计值

(4)试验结果与各国规范计算值的比较结果表明,我国规范考虑冷弯效应的屈服强度计算公式对于全截面有效的冷弯厚壁型钢也是适用的，且略偏于保守.

[1]于炜文, 董军, 夏冰青. 冷成型钢结构设计[M]. 3版. 北京: 中国水利水电出版社, 知识产权出版社, 2003.

YU Weiwen, DONG Jun, XIA Bingqing. Cold-formed steel design[M]. 3rd ed. Beijing: China Water Power Press, Intellectual Property Right Press, 2003.

[2]温东辉. 冷弯厚壁钢管压弯构件抗震性能研究[D].上海：同济大学，2014.

WEN Donghui. Research on seismic performance of cold-formed thick-walled steel tubular beam-columns[D]. Shanghai: Tongji University, 2014.

[3]Zhu J H, Young B. Aluminum alloy circular hollow section beam-columns[J]. Thin-walled Structures, 2006, 44(2):131.

[4]Young B. Experimental and numerical investigation of high strength stainless steel structures[J]. Journal of Constructional Steel Research, 2008, 64(11):1225.

[5]Loughlan J. Thin-walled cold-formed sections subjected to compressive loading[J]. Thin-Walled Structures, 1993, 16(1/2/3/4) :65.

[6]沈祖炎,李元齐,王磊,等.屈服强度550 MPa高强冷弯薄壁型钢结构轴心受压构件可靠度分析[J].建筑结构学报，2006, 27(3):26.

SHEN Zuyan, LI Yuanqi, WANG Lei,etal. Reliability analysis of 550 MPa high-strength cold-formed thin-walled steel structures [J]. Journal of Building Structures, 2006, 27(3): 26.

[7]高恒. 中厚壁冷弯钢管柱轴压承载力试验研究与分析[D].武汉：武汉理工大学, 2007.

GAO Heng. Experimental research and FEM simulation of ultimate axial compression of cold-formed medium wall hollow steel coluns[D]. Wuhan: Wuhan University of Technology, 2007.

[8]王莉萍. 厚壁冷弯型钢冷弯效应研究[D].上海：同济大学，2011.

WANG Liping. Experimental investigation on cold-forming effect of thick-walled steel sections[D].Shanghai:Tongji University, 2011.

[10]沈祖炎，温东辉，李元齐，等. 冷弯厚壁钢管截面的材料特性分布模型[J].同济大学学报：自然科学版，2016，44(7): 981.

SHEN Zuyan, WEN Donghui, LI Yuanqi,etal. Distribution models of material properties for the cross-section of cold-formed thick-walled steel rectangular tubes[J]. Journal of Tongji University: Natural Science, 2016, 44(7): 981.

[13]The Joint Standards Australia/Standards New Zealand Committee. AS/NAS 4600:2005 Cold-formed steel structures [S]. Sydney: Standards Australia/ Standards New Zealand, 2005.

[14]Britain Standard Institute. BS EN 1993-1-6:2006 Eurocode 3: Design of steel structures [S]. London: Britain Standard Institute, 2006.

Experimental Research on Cold-Formed Thick-Walled Steel Box Stubs and Comparison of Results with Related Codes

WEN Donghui1,2, SHEN Zuyan1,3, LI Yuanqi1,3, ZHU Shaowen4

(1.College of Civil Engineering, Tongji University, Shanghai 200092,China; 2. Department of Structural Engineering, Taiyuan University, Taiyuan 030032, China; 3. State Key Laboratory of Disaster Redcution in Civil Engineering, Tongji University, Shanghai 200092, China; 4. Hankou Roll Forming-Steel Plant of WISCO, Wuhan 430035, China)

Sixteen specimens were tested under axial compression to investigate the effect of cold-forming process on the behavior of stub columns. The main parameters varied in the tests were the width-thickness ratio of steel tubes. The test results indicate that the shape of load-displacement curves depends mainly on the width-thickness ratio of cross-sections. When the width-thickness ratio is relatively small, the axial load decreases slowly after the peak ponit of the curve and the total axial displacement is relatively large before failure. On the contrary, the effect of local buckling on the load-displacement curves is significant, which results in the sharp declining of curves after the peak point when the with-thickness is rather large. Meanwhile, the calculation results of related standards considering the cold-forming effects were compared with the experimental results. The comparison show that the formula for calculating the yielding strength of cold-Formed thin-Walled sections considering the cold-forming effects in Chinese Technical Code of Cold-Formed Thin-Walled Steel Structures(GB50018-2002) is suitable for those cold-formed thick-walled steel stubs with local buckling restrained.

cold-formed thick-walled tube; stub column; cold-forming effect; specification formula; width-thickness ratio

2015-12-23

国家自然科学基金重点项目(51538002);国家自然科学基金(51178330)

温东辉(1982—)，女，讲师，工学博士，主要研究方向为冷弯型钢结构抗震性能.E-mail:wendh9@163.com

沈祖炎(1935—)，男，教授，中国工程院院士，主要研究方向为钢结构.E-mail:zyshen@tongji.edu.cn

TU391；TU392.3

A