使用新算法的剪切型子结构振动台试验稳定性
2016-09-20蒋欢军
傅 博, 蒋欢军
(1. 同济大学 土木工程学院,上海 200092; 2. 同济大学 土木工程防灾国家重点实验室,上海 200092)
使用新算法的剪切型子结构振动台试验稳定性
傅博1, 2, 蒋欢军1, 2
(1. 同济大学 土木工程学院,上海 200092; 2. 同济大学 土木工程防灾国家重点实验室,上海 200092)
提出了使用无条件稳定显式Chen-Ricles(CR)积分新型算法的剪切型子结构振动台试验方法,包括子结构划分以及试验流程图.通过推导子结构的运动方程进行子结构方法的数值验证,考虑了两种不同量级试验子结构频率的情况.结果表明:当试验子结构频率较小时,子结构方法可以保证稳定性和准确性,反之则不能.最后利用离散控制理论推导出子结构方法方框图的离散闭环传递函数,通过求解传递函数的极点位置判断离散系统的稳定性,进一步论证了数值模拟发现的结果.
子结构; 振动台试验; 稳定性; 离散控制理论
传统的抗震试验方法包括拟静力试验、振动台试验和拟动力试验.振动台试验通过直接输入地震动加速度或位移来驱动振动台,从而可直接研究试验对象的抗震性能.由于振动台台面尺寸和承载力等限制,超高层建筑结构等大型结构必须以很小的缩尺模型进行试验,而尺寸效应会严重影响振动台试验结果的准确性.通过引入子结构技术,拟动力试验将整体结构中较难准确进行数值模拟的部分或构件进行试验,为试验子结构,剩余的部分进行数值模拟,为分析子结构,因此拟动力试验亦被称作混合模拟试验.由于数值积分算法、计算机计算效率、作动器性能以及控制等因素的限制,传统混合模拟试验加载速率较慢.近年来,由于越来越多的研究评估带有速度依赖性阻尼器的结构抗震性能,因此传统的混合模拟试验已无法满足其要求而逐渐发展为实时混合模拟试验.
实时混合模拟试验的“实时”要求分析子结构计算得到的位移或者力实时地加载到试验子结构上,无疑对积分算法的效率提出了很高的要求.在计算时间上,显式积分算法由于不用迭代明显优于隐式积分算法.然而,传统的显式积分算法皆为条件性稳定,意味着系统的最高频率不能太大,否则需要很小的时间步长方可满足稳定性要求.近年出现的新型积分算法如Chen和Ricles提出的CR算法[1]兼具无条件稳定和显式两种特性,故具有很高的计算效率,非常适合实时混合模拟试验[2-4].
与传统混合模拟试验类似,绝大部分已有实时混合模拟试验采用作动器作为加载设备,给试验子结构施加位移,测出恢复力作为反馈,这要求试验子结构的惯性力相对较小可以忽略.如果试验子结构惯性力不能忽略时,子结构振动台试验(振动台加载型实时混合模拟试验)可以准确地反映试验子结构的惯性力.这种试验方法尤其适合上部带有附属结构或设备(如调谐质量阻尼器(TMD)[5-6]、调谐液体阻尼器(TLD)[7-8])的主体结构,附属结构和主体结构分别作为试验子结构和分析子结构.最近,Mosalam和Günay[9]将子结构振动台试验方法推广至评估高压电立式断路隔离开关的抗震性能,下部支撑结构和上部绝缘支柱分别作为分析子结构和试验子结构.同时,子结构振动台试验技术还被用于研究土-结构相互作用问题[10-11],上部结构和下部土体分别作为试验子结构和分析子结构.此外还有少量关于振动台和作动器联动加载型实时混合模拟试验的研究[12-14].
大部分子结构振动台试验研究中分析子结构的最高频率较小,即便使用条件性稳定积分算法(如中心差分法、显式Newmark算法和线性加速度法)来求解分析子结构运动方程,也无需很小的时间步长来满足积分算法的稳定,故以往研究者鲜有关心积分算法的稳定性问题.然而当分析子结构最高频率较大时,积分算法的选取显得格外重要.由于CR算法提出的时间不长,有关该算法在子结构振动台试验的适用性的研究非常少.Zhu[15]等人研究了使用CR积分算法子结构振动台试验方法的稳定性,但是该方法的建立基于求解整体结构的运动方程而非求解分析子结构的运动方程,无疑在原理上与子结构方法相悖.
根据上述研究背景,本文首先针对两层剪切型结构提出了采用CR积分算法的子结构振动台试验方法,包括子结构的划分和试验的流程图;基于运动方程进行了子结构方法的数值模拟验证,结果表明不同量级的试验子结构的频率会造成子结构方法不同的稳定性;最后,利用离散控制理论进一步论证了数值模拟的结果.
1 试验方法
1.1子结构的定义
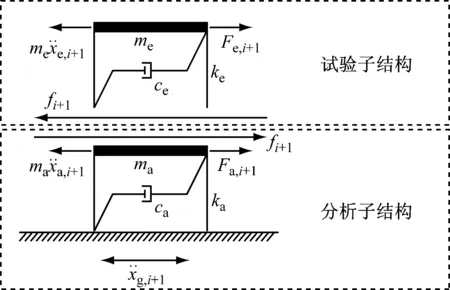
图1 子结构的定义
1.2试验流程
根据分析子结构的隔离体受力图可得到其下一时间步的运动方程
(1)

(2)
(3)
式中:Δt为积分时间步长;αa,1和αa,2为积分参数
(4)
根据式(1)可得分析子结构下一时间步的加速度为
(5)
需要注意的是,式(5)只适用于分析子结构为线弹性时,更一般的情形可以用分析子结构的恢复力Ra,i+1替代kaxa,i+1,式(5)进行相应的修改,在此不再赘述.
求解式(5)仍需要下一时间步的界面力fi+1,可通过试验子结构(图2)测得.
图2中u为绝对位移.对于两层剪切型结构而言,界面处的位移与分析子结构的位移相同;根据位移协调条件,界面处的位移为绝对位移,而非式(3)计算出的相对位移,绝对位移与相对位移的关系如下:
(6)
综上可得两层剪切型结构使用CR算法的子结构振动台试验流程图(图3).本文所提的试验流程图很容易推广至两层剪切型结构使用其他显式积分算法的子结构振动台试验方法.
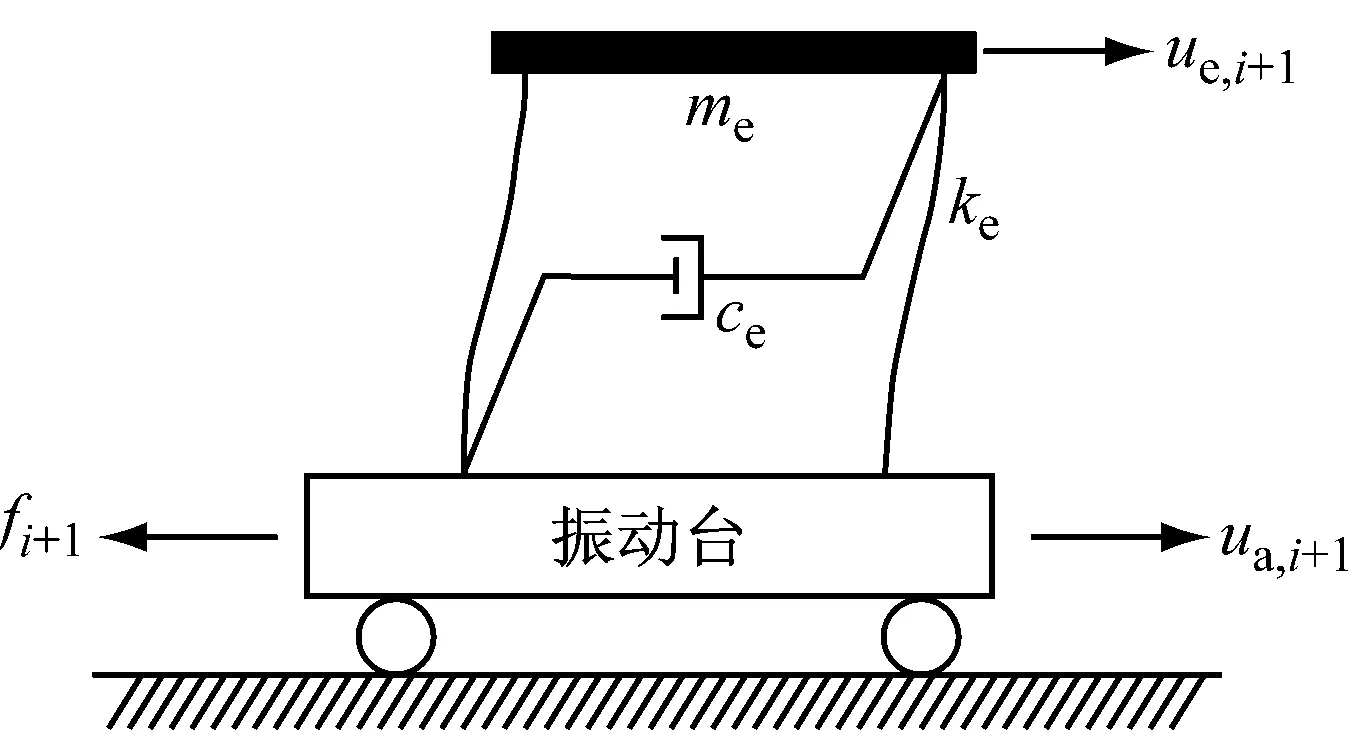
图2 试验子结构的加载模式
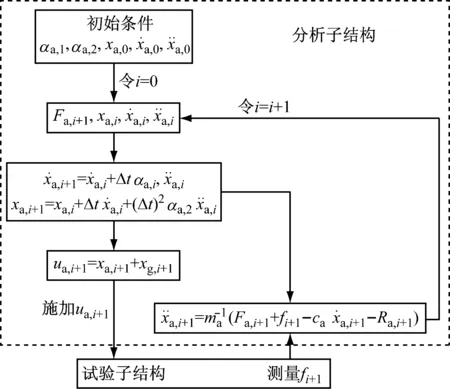
图3 两层剪切型结构使用CR算法子结构振动台试验流程
2 子结构方法的数值模拟验证
由上文可知,界面力在整个试验过程中起到重要的作用.因此,在子结构方法进行数值模拟验证时,关键在于如何得到较精确的界面力.
根据试验子结构的隔离体受力图可以得到界面力的表达式
(7)

(8)
(9)
(10)
(11)

将上述方法应用到两个具有不同量级的试验子结构频率的例子验证时,发现试验子结构频率较小时,子结构方法可以得到稳定并较为准确的结果;而当试验子结构频率较大时,子结构方法无法得到稳定的结果.
2.1频率较小的试验子结构
本算例的子结构基本参数为:ma=me=300 kg;ωa=ωe=10 rad·s-1;ξa=ξe=0.02;ka=ke=30 000 N·m-1;ca=ce=120 N·s·m-1;时间步长Δt=0.01 s.ω和ξ分别代表圆频率和阻尼比.
El Centro NS, 1940地震波作为地震动输入,同时采用整体结构分析和子结构方法进行分析.整体结构分析也使用CR积分算法,所用的参数与子结构方法相同.两种方法得到的首层结构位移(分析子结构的位移)对比如图4所示.

图4 首层结构位移反应对比
使用归一化均方误差来量化子结构方法得到的首层结构位移的精度,定义如下:
(12)
式中:E为误差;n为采样点,即总的数值积分步数;下标cm和rm分别为计算模型(computing model)和参考模型(reference model).这里的计算模型和参考模型分别对应的是子结构分析方法和整体结构分析.根据式(12)计算出的误差值为0.71%,说明子结构方法具有较高的精度.
2.2频率较大的试验子结构
与上例相比,本算例试验子结构的频率增大100倍,即ωe=1 000 rad·s-1,试验子结构的刚度和阻尼也相应增大,其余结构参数和时间步长均不变.结果发现使用子结构方法得不到稳定的结果.这表明当试验子结构频率较大时,CR积分算法将无法保证其无条件稳定性.作者将在下文利用离散控制理论分析论证这一结论.
3 子结构方法的稳定性分析
3.1闭环离散传递函数
根据离散控制理论[16],离散时间系统的稳定性可通过其闭环传递函数极点(即分母为0时的根)的位置来判断.若极点都处于单位圆之上或内部,系统稳定;反之,系统不稳定.
根据前文所述各个物理量的关系,对时间域下的变量进行Z变换[16],可得到两层框架子结构方法方框图(图5),从而可得到系统的闭环离散传递函数.表1列出图5中所有时域信号对应的Z变换变量.表1中Z变换变量下标acc,disp和vel分别代表加速度、位移和速度.

表1 Z变换

图5 两层剪切型结构子结构方法方框图
从图5可以看出,该离散系统为单输入单输出系统,输入为地震动加速度,输出为分析子结构的相对位移.图5中各个量的关系部分可从公式(1)和(7)得到,其余部分见下面公式:
(13)
(14)
其中,公式(13)和(14)为等效地震力的定义;公式(15)由公式(8)变换顺序得到.将式(13)~(15)进行Z变换并联立,最终可得闭环离散传递函数的表达式:
(16)
式中:Gcl(z)为系统的闭环离散传递函数;G1(z),G2(z)和G3(z)为由积分算法得到的离散传递函数.将公式(1)~(3)进行Z变换并联立,可以求得传递函数G1(z)和G2(z)的表达式;将公式(9),(10)和(14)进行Z变换并联立,可以求得传递函数G3(z)的表达式

(17)

(18)
(19)
式(17)~(19)分子与分母的系数如下:
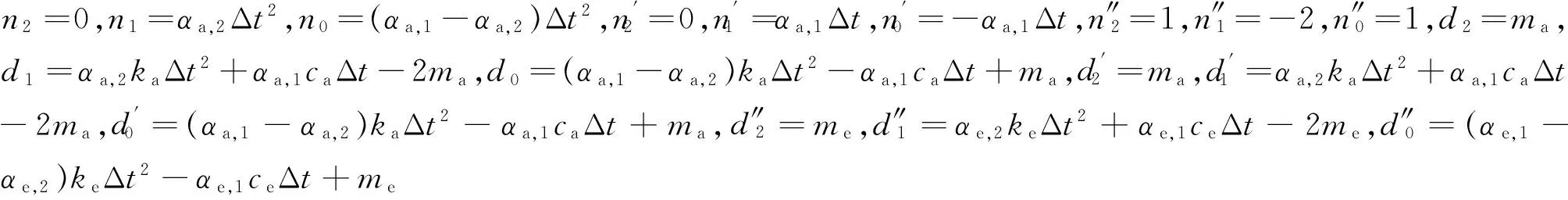
将式(17)~(19)带入公式(16)可得闭环离散传递函数的最终表达式
(20)
式(20)中分子和分母的系数如下:
N3=n1[(me)2n″2-mad″2-med″2]
N2=n0[(me)2n″2-mad″2-med″2]+n1[(me)2n″1-mad″1-med″1]
N1=n0[(me)2n″1-mad″1-med″1]+n1[(me)2n″0-mad″0-med″0]
N0=n0[(me)2n″0-mad″0-med″0]
D4=d2d″2
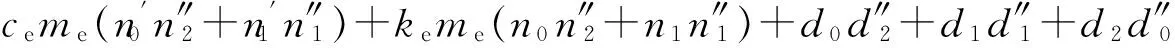

3.2稳定性分析
由公式(20)可看出闭环离散传递函数分母为z的四阶表达式,表明系统有4个极点.
当子结构的结构参数及时间步长已知,子结构的积分参数可由公式(4)和(11)求得;从而可求出G1(z),G2(z)和G3(z)分子和分母的系数;进而可求得闭环离散传递函数最终表达式中分子、分母系数,这样便可通过极点位置来判断系统的稳定性.
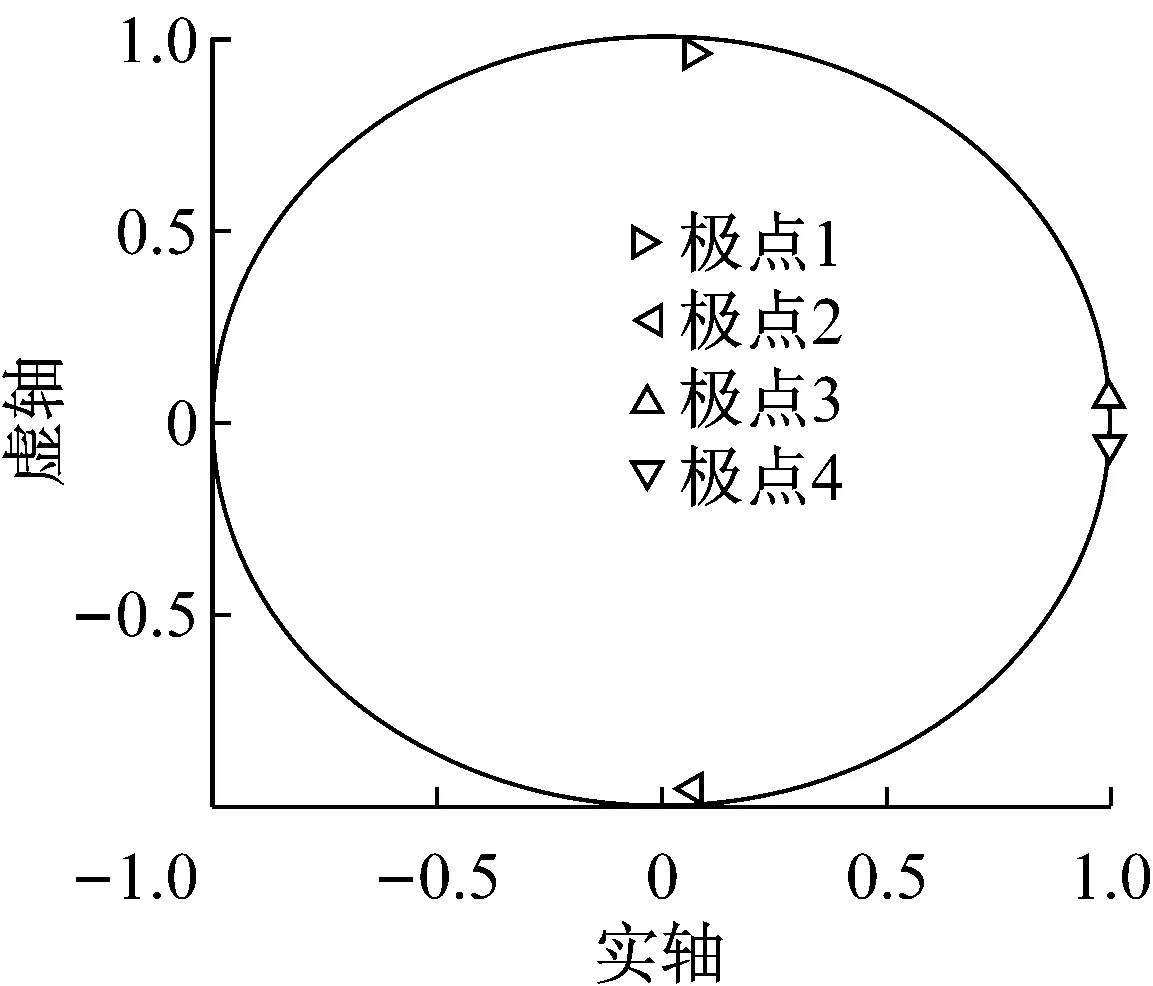
使用第2.1节的结构参数和时间步长,为进一步论证试验子结构频率对离散系统稳定性的影响,ωe取10,100和1 000 rad·s-1三个值.图6显示离散闭环传递函数极点的位置,可知当ωe取10和100 rad·s-1时,4个极点全都位于单位圆内,表明系统稳定;当ωe=1 000 rad·s-1时,极点1位于单位圆外,表明系统不稳定.这一结果很好地论证了本文的数值模拟结果.
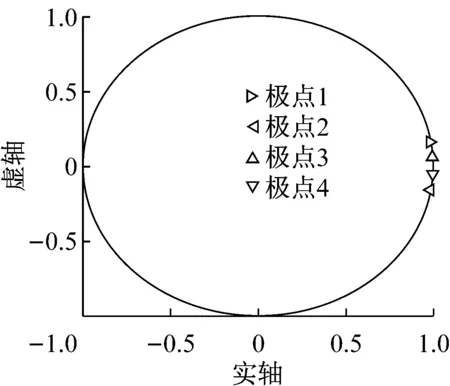
a ωe=10 rad·s-1
b ωe=100 rad·s-1

c ωe=1 000 rad·s-1
4 结论及展望
(1) 利用离散控制理论可有效地论证本文所提出的子结构方法.
(2) 当试验子结构频率相对较小时,使用CR积分算法的子结构振动台试验方法能保证其稳定性,并且与整体结构分析比较有较高的精度.
(3) 当试验子结构频率相对较大时,使用CR积分算法的子结构振动台试验方法会失去稳定性,仍需要进一步的研究.
(4) 与文献[2]对比发现,CR积分算法应用到作动器加载型实时混合模拟试验和子结构振动台试验两种试验方法时稳定性差异很大.而且后者的稳定性分析更加复杂.前者不存在试验子结构(一般只是结构构件)的频率大小问题,在没有时滞时,CR积分算法将会保持其稳定性;而对于后者,如果试验子结构频率较大时,即便没有时滞CR算法也会失去稳定性.
此外,本文所提出的试验方法基于一些假定,仍需进一步的试验验证.而且试验成功与否除了取决于积分算法的稳定性,还在很大程度上取决于试验水平和仪器精度等因素.
[1]CHEN Cheng, Ricles J. Development of direct integration algorithms for structural dynamics using discrete control theory [J]. Journal of Engineering Mechanics: ASCE, 2008, 134(8): 676.
[2]CHEN Cheng, Ricles J, Marullo T M,etal. Real-time hybrid testing using the unconditionally stable explicit CR integration algorithm [J]. Earthquake Engineering & Structural Dynamics, 2009, 38(1): 23.
[3]CHEN Cheng, Ricles J, Karavasilis T,etal. Evaluation of a real-time hybrid simulation system for performance evaluation of structures with rate dependent devices subjected to seismic loading [J]. Engineering Structures, 2012, 35: 71.
[4]CHEN Cheng, Ricles J. Large-scale real-time hybrid simulation involving multiple experimental substructures and adaptive actuator delay compensation [J]. Earthquake Engineering & Structural Dynamics, 2012, 41(3): 549.
[5]Horiuchi T, Inoue M, Konno T. Development of a real-time hybrid experimental system using a shaking table [C/OL]∥ Proceedings of 12th World Conference on Earthquake Engineering. Auckland: New Zealand Society for Earthquake Engineering, 2000. [2015-10-30]. http:∥www.iitk.ac.in/nicee/wcee/article/0843.pdf.
[6]Igarashi A, Iemura H, Suwa T. Development of substructured shaking table test method [C/OL]∥ Proceedings of 12th World Conference on Earthquake Engineering. Auckland: New Zealand Society for Earthquake Engineering, 2000. [2015-10-30]. http:∥www.iitk.ac.in/nicee/wcee/article/1775.pdf.
[7]Lee S K, Park E C, Min K W,etal. Real-time hybrid shaking table testing method for the performance evaluation of a tuned liquid damper controlling seismic response of building structures [J]. Journal of Sound and Vibration, 2007, 302(3): 596.
[8]Malekghasemi H, Ashasi-Sorkhabi A, Ghaemmaghami A R,etal. Experimental and numerical investigations of the dynamic interaction of tuned liquid damper-structure systems [J]. Journal of Vibration and Control, 2015, 21(14): 2707.
[9]Mosalam K M, Günay S. Seismic performance evaluation of high voltage disconnect switches using real-time hybrid simulation: I. System development and validation [J]. Earthquake Engineering & Structural Dynamics, 2013, 43(8): 1205.
[10]WANG Qiang, WANG Jinting, JIN Feng,etal. Real-time dynamic hybrid testing for soil-structure interaction analysis [J]. Soil Dynamics and Earthquake Engineering, 2011, 31(12): 1690.
[11]ZHOU Mengxia, WANG Jinting, JIN Feng,etal. Real-time dynamic hybrid testing coupling finite element and shaking table [J]. Journal of Earthquake Engineering, 2014, 18(4): 637.
[12]Shao X, Reinhorn A M, Sivaselvan M V. Real-time hybrid simulation using shake tables and dynamic actuators [J]. Journal of Structural Engineering: ASCE, 2010, 137(7): 748.
[13]Nakata N, Stehman M. Substructure shake table test method using a controlled mass: formulation and numerical simulation [J]. Earthquake Engineering & Structural Dynamics, 2012, 41(14): 1977.
[14]彭天波,谢馨,曾忠,等. 采用Chang方法的混合试验的稳定性和精度[J]. 同济大学学报:自然科学版, 2014, 42(12): 1790.
PENG Tianbo, XIE Xin, ZENG Zhong,etal. Stability and accuracy of shaking table-actuator hybrid test with Chang method [J]. Journal of Tongji University: Natural Science, 2014, 42(12): 1790.
[15]ZHU Fei, WANG Jinting, JIN Feng,etal. Stability analysis of MDOF real-time dynamic hybrid testing systems using the discrete-time root locus technique [J]. Earthquake Engineering & Structural Dynamics, 2015, 44(2): 221.
[16]Ogata K. Discrete-time control systems [M]. 2nd ed. Upper Saddle River: Prentice Hall, 1995.
Stability of Shear-Type Substructure Shaking Table Testing Using a New Algorithm
FU Bo1, 2, JIANG Huanjun1, 2
(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
A shear-type substructure shaking table testing (SSTT) method, which includes the substructure partition and the testing flowchart, was proposed using the unconditionally stable explicit Chen-Ricles (CR) new integration algorithm. The substructure method was numerically verified by deducing the equations of motion (EOMs) of the substructures. Two cases with different magnitudes of the frequency for the experimental substructure were considered. The results show that the stability and the accuracy of the substructure method can be guaranteed if the frequency of the experimental substructure is relatively small, and vice versa. Finally, the discrete control theory was applied to deduce the discrete closed-loop transfer function of the block diagram for the substructure method. In addition, the locations of the poles for the transfer function was used to judge the stability of the discrete system so as to further demonstrate the findings from the numerical simulation.
substructure; shaking table testing; stability; discrete control theory
2015-10-30
国家自然科学基金(51478354)
傅博(1990—),男,博士生,主要研究方向为抗震试验方法. E-mail:fubo2006_2006@126.com
蒋欢军(1973—),男,教授,博士生导师,工学博士,主要研究方向为高层及超高层结构抗震. E-mail:jhj73@tongji.edu.cn
P315.8
A
