一种适用复杂非线性黑箱系统的参数灵敏度分析方法
2016-09-20邓辉咏孙海涛
邓辉咏,王 炎,郝 刚,孙海涛
(1.军械工程学院,河北 石家庄 050003;2.66442部队分库,山西 阳泉 045233)
一种适用复杂非线性黑箱系统的参数灵敏度分析方法
邓辉咏1,王炎2,郝刚1,孙海涛1
(1.军械工程学院,河北 石家庄050003;2.66442部队分库,山西 阳泉045233)
主要研究了全局灵敏度分析法在解决实际问题中的优点和不足,提出了基于均值和方差的多个局部灵敏度参数评价全局灵敏度,并用多属性决策机制进行灵敏度排序的双参数灵敏度分析方法。该方法克服了单一参数评价全局灵敏度的缺陷,不需知道输入变量和输出响应的分布规律,可以采用较少的数据量得到可信的结果,为复杂非线性黑箱系统参数灵敏度分析提供了新的思路,通过实例验证了本方法的有效性和可信性。
灵敏度分析;非线性系统;双参数;黑箱系统
灵敏度分析是一种研究基本输入变量的不确定性在其输出响应不确定性分配的技术,是概率风险评估问题的主要组成[1],现已广泛运用到了影响目标性能的关键因素筛选上,葛建立等采用灵敏度分析法提取了9个对自行火炮底盘俯仰角幅值较大的因素[2];张猛等利用灵敏度分析从60个结构件中提取9个对车身弯曲刚度、扭转刚度、一阶扭转频率和车身质量影响较大的结构件[3]。
灵敏度分析方法有局部灵敏度分析和全局灵敏度分析。局部灵敏度分析法主要有:直接求导法、有限差分法和格林函数法。局部灵敏度分析只能获得某个点(或较小区间段)的灵敏度,其反映的是某个输入参数在初值附近的变化对输出的影响,无法对输入参数在整个取值空间及参数之间的共同作用作出估计。全局灵敏度能够对输入参数在整个取值空间的作用作出估计。
1 全局灵敏度分析法的优点和不足
1.1全局灵敏度分析法的优点和不足
全局灵敏度分析法主要有:非参数方法灵敏度分析、基于方差的灵敏度分析和矩独立方法灵敏度分析3类[4]。
非参数方法灵敏度分析主要包括:Pearson相关系数灵敏度分析、标准回归系数灵敏度分析、偏相关系数灵敏度和Spearman相关系数灵敏度分析。采用非参数方法的优点在于考虑了基本输入变量与输出响应量之间的相关关系,文献[5]指出,该方法对于非线性模型,不能有效地反映目标函数值随设计变量变化的程度。
基于方差的灵敏度分析最早由Nakashima和Yamato提出,包括Heltoh、Andsten-vaurio、sobol一阶矩、sobol全效应等灵敏度。基于方差的灵敏度分析侧重于衡量基本输入变量对其输出响应量的方差贡献程度,优点是考虑了基本输入变量在整个取值范围内对输出响应的贡献以及基本输入变量的交互关系,但由于包含了方差,能够充分描述输出响应的不确定性的隐含条件,Oakley和Ohagan在文献[6]中指出,采用单一的方差作为灵敏度分析结果,会导致决策错误。Borgonovo在文献[7]中指出,描述输出响应变化时,方差并不总是充分的,灵敏度应当是一个完整的输出响应分布,而并非某一个特殊的矩。
矩独立方法灵敏度分析是Borgonovo提出的一种基本输入变量对其响应量分布影响的灵敏度分析方法[8],其优点在于考虑了输出响应量的整个分布,但由于灵敏度指标过于单一,没有全面顾及变量的单独影响和变量之间的交互作用,且由于采用蒙特卡洛法进行求解,计算量太大。
对于大型复杂非线性系统,例如以射击精度为目标的自行火炮系统,其输入与输出之间很难用一个明确的数学关系式描述。
文献[9]用Simulink建立某机电系统的仿真模型,再运用Simlab软件进行灵敏度分析,得到灵敏度分析结果,其优点是采用仿真软件建立了输入与输出的关系,缺点是用Simlab进行灵敏度计算时,需要明确输入变量的分布关系。
也有文献采用神经网络[10]、支持向量机(SVM)[11]等建立输入与输出的关系,进而用灵敏度分析法分析各输入参数的灵敏度。采用这种方法的缺点是:要获得较高的预测精度,须有大量原始数据作为支撑。
对于自行火炮系统,大量的射击试验费效比较低,且由于这种物理测试方法很难控制结构参数的变化,如间隙由于射击的不断进行而退化变大;弹簧刚度由于疲劳退化而变小,因此,现有的全局灵敏度分析法都不是解决自行火炮这样大型非线性系统灵敏度问题的有效方法。虚拟样机技术则不存在这个问题,它可以用较少的试验数据,验证虚拟样机的有效性和正确性;另外,虚拟样机上可以保持其他参数不变,很精确地控制摄动参数,研究摄动参数对系统的影响。但虚拟样机技术对于大型复杂非线性系统,存在计算效率较低,计算量大,不适宜做大量的仿真试验的缺陷。
文献[12]将全局区间分成多个小区间的方法进行分析,使各个小区间满足Δb足够小的条件,认为目标函数值在小区间上线性变化的,用该区间上的差商代替这个区间的灵敏度,然后对各个区间的灵敏度进行求和得到全局灵敏度,是一种由局部评价全局的有效尝试。该方法为全局灵敏度的求取开拓了思路,但仍有其局限性。
1.2现有局部灵敏度评价全局灵敏度的不足
假设某4个参数在可行域(a,e)内对其目标函数的关系分别为z1(x)、z2(x)、z3(x)和z4(x),如图1所示。
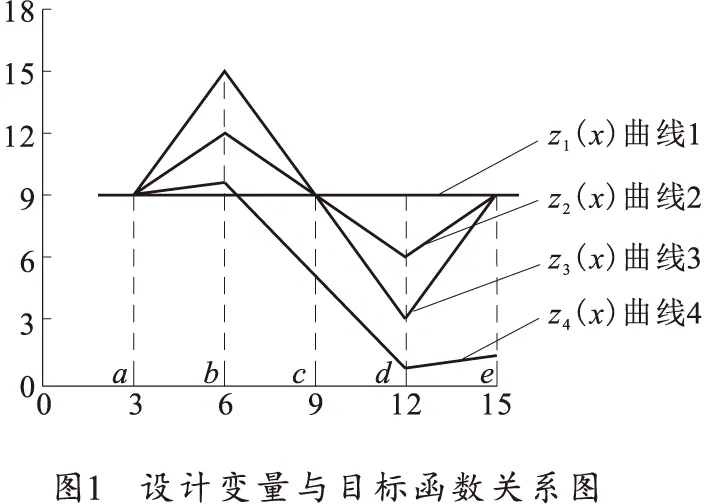
采用有限差分法计算局部灵敏度,反映到图1中即为该参数在某局部域的斜率。域(a,b)和域(d,e)各曲线的斜率分别为:k1=0、k2=1、k3=2、k4=1/3;域(b,c)和域(c,d)各曲线的斜率分别为:k1=0、k2=-1、k3=-2、k4=-5/3。若按文献[3]的方法,将可行域(a,e)分成(a,b)、(b,c)、(c,d)和(d,e)4个局部域,各局部域满足有限差分法计算局部灵敏度的条件,根据其定义式,在局部域上的斜率即可代表该域内的灵敏度。从图1中可看出,在域(a,b)和域(d,e)上满足关系:s3>s2>s1;而在域(b,c)和域(c,d)上则满足关系:s3
2 双参数全局灵敏度分析法
2.1相关定义和算法
定义:双参数全局相对灵敏度分析是指将参变量x相对目标函数f(x)在区间[a1,an+1]变化,以Δb为长度,将区间[a1,an+1]分成有限个小区间[a1,a2]、[a2,a3]、…、[an,an+1],且满足[a1,an+1]=[a1,a2]∩[a2,a3]∩…∩[an,an+1],当Δb较小时,认为f(x)在任一子区间[ai,ai+1]为线性变化,根据局部灵敏度的定义,该区间上的斜率即为其灵敏度
(1)
式中,ai、 f(ai)分别为区间端点的参量值和目标函数值。
由于不同的参变量有不同的量纲,而目的是要分析所有参变量在其整个区间上的灵敏度,须所有的参变量放在同一尺度进行评价,即进行标准化处理,取向量a={a1,a2,…,an+1},则
(2)
式中,E={1,1,…,1}1×n。则第i个区间上的相对灵敏度可表示为
(3)
式中,f(a0)为目标函数在初值上函数值,是为消除不同目标函数值之间量纲的不同而引入的量,如果目标函数只有一个,则可不列。
(4)
(5)
显然,若均值和方差均比较大,该因素灵敏度排序靠前;若均值排序靠前,方差排序靠后,或者反之,其灵敏度如何评价,则涉及到多属性决策问题。
2.2DGSA法的决策机制
如何用均值和方差两个量来进行排序,得到最终的结果,显然是一个多属性决策问题。对于多属性决策的方法有模糊法、灰色法、聚类法和Topsis法。Topsis法即逼近理想解的排序方法,是求解多属性决策问题的典型方法之一,这种方法通过构造多属性问题的理想解和负理想解,并以靠近理想解和远离理想解两个评价判据为基准,对各样本进行排序。该方法对样本量、指标多少及数据的分布没有特殊限制,较适合用于双参数全局相对灵敏度的排序,Topsis法的决策机制参考文献[13],这里不再赘述。
2.3复杂非线性黑箱系统的灵敏度分析流程
非线性黑箱系统DGSA分析法的分析流程如图2所示。
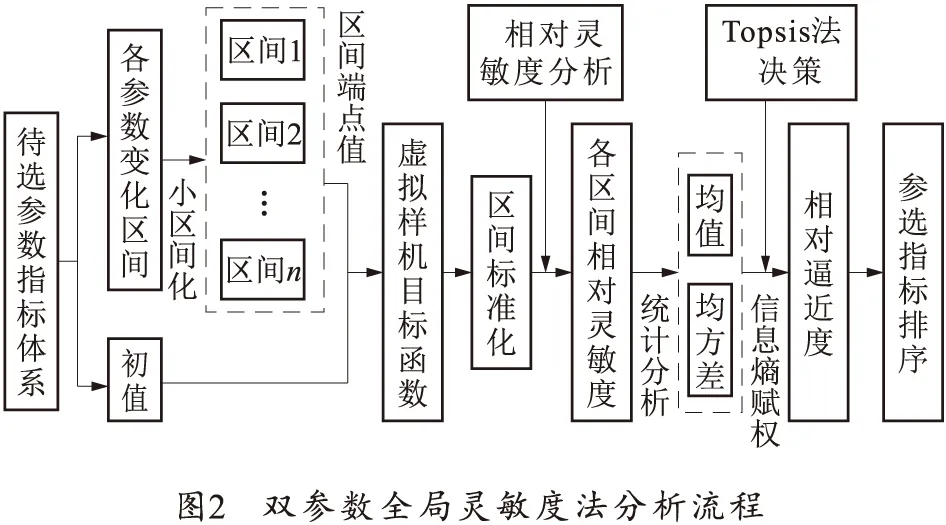
需要说明的是,当各参数区间化时,如果区间的长度不一致,求取均值和方差时应该考虑区间长度的影响,以各个区间长度占总区间长度计为各个区间的权重,将权重的影响放到计算均值和方差中。
3 DGSA法的验证
以图1中的4条曲线为研究对象,应用Topsis法进行决策排序时,需要知道目标函数的理想解和负理想解,对于归一化的均值、方差,若其均值和方差均为1,则应该排序靠前,因此,可构造理想解和负理想解为
A*={1,1},A-={0,0}
(6)
通过信息熵求取的均值和方差的权值为:{0.8,0.2},通过编制Matlab程序得到各个曲线的相对逼近度(全局相对灵敏度),表1为采用DGSA法得到的计算结果。
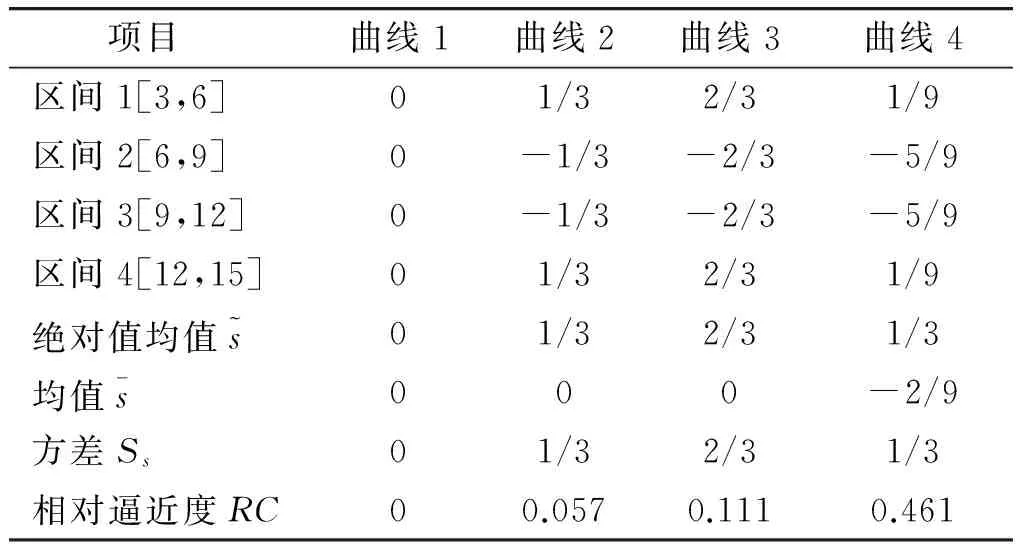
表1 双参数全局相对灵敏度分析举例结果表
从表1可知,参数x对曲线1、2、3的相对逼近度排序结果为:RC1 由于在求取局部灵敏度时,摄动一个参数而保持其他参数不变,没有考虑各因素之间的交互作用,因此该方法在因素交互作用明显的系统进行参数灵敏度分析时,其排序精度还有待进一步验证。 通过分析现有全局灵敏度分析法的优点及其在解决大型非线性系统方面的不足,提出了采用可行域内多个局部灵敏度的均值和方差评价全局灵敏度,并用Topsis多属性决策机制进行排序的双参数全局灵敏度分析法(DGSA)。 笔者研究了非线性黑箱系统的DGSA法分析流程,并对其有效性和可信性进行了验证。采用了双参数评价全局灵敏度,克服了单一参数评价的缺陷,在计算过程中不需要知道输入变量与输出响应的分布,且计算量相对较小,较适用于大型复杂非线性黑箱系统的灵敏度分析。 References) [1]SALTELLI A. Sensitivity analysis for importance assessment[J]. Risk Anal, 2002, 22(3):579- 590. [2]葛建立,杨国来,曾晋春,等. 某自行火炮总体结构参数灵敏度分析与优化[J]. 火炮发射与控制学报,2007(3):16-18. GE Jianli, YANG Guolai, ZENG Jinchun, et al. Sensiti-vity analysis and optimization of integrated structural parameters for a type of wheeled self-propelled gun[J]. Journal of Gun Launch & Control, 2007(3):16-18.(in Chinese) [3]张猛,陈勇敢,陈剑. 灵敏度分析在车身结构优化设计中的应用[J]. 汽车科技,2011(3):22-24. ZHANG Meng, CHEN Yonggan, CHEN Jian. Application of sensitivity analysis in the optimization design of car-body[J]. Auto Mobile Science & Technology, 2011(3):22-24. (in Chinese) [4]韩林山. 浅析灵敏度分析的几种数学方法[J]. 中国水运, 2008, 8(4): 177-178. HAN Linshan. Several mathematical methods of Sensitive analysis[J]. China Water Transport, 2008, 8(4):177- 178.(in Chinese) [5]FREY C H, PATIL S R. Identification and review of sensitivity analysis methods[J]. Risk Anal, 2002, 22(3): 553-571. [6]OAKLEY J E,OHAGAN A.Probalilistic sensitivity analy-sis of complex models:a bayesian approach[J]. Journal of the Royal Statistical Society:Series B (Statistical Metho-dologh), 2004, 66(3): 751-769. [7]BORGONOVO E. Measuring uncertainty importance:investigation and comparison of alternative approaches[J]. Risk Anal, 2006, 26(5): 1349-1461. [8]BORGONOVO E.A new uncertainty importance measure[J].Reliabity Engeering System Saf,2007,92(6):771-784. [9]李会先. MATLAB/SIMULINK与SIMLAB联合进行不确定性、灵敏度分析的框架[J]. 科技创业家,2012(7):161-163. LI Huixian. Uncertainty and sensitivity analysis frame by MATLAB/SIMULINK and SIMLAB[J]. Technological Pioneers,2012(7):161-163.(in Chinese) [10]谢桂兰,贺礼财,肖春芽.基于BP网络的蜂窝铝芯力学性能预测与灵敏度分析[J]. 材料导报,2014,28(12):144-147. XIE Guilan, HE Licai, XIAO Chunya. Mechanical properties prediction and sensitivity analysis for aluminum honeycomb core structure based on BP neural network[J]. Materials Review, 2014, 28(12):144-147.(in Chinese) [11]赵金钢,赵人达,占玉林,等.基于支持向量机和蒙特卡洛法的结构随机灵敏度分析方法[J]. 工程力学,2014,31(2):195-202. ZHAO Jingang, ZHAO Renda, ZHAN Yulin, et al. Stochastic sensitivity analysis method based on support vector machine and Monte Carlo[J]. Engineering Mecha-nics, 2014, 31(2):195-202. (in Chinese) [12]蔡文勇. 大口径车载火炮多柔体动力学与总体优化研究[D]. 南京: 南京理工大学, 2008. CAI Wenyong. Study on flexible multi-body dynamics and overall parameters optimization for large caliber vehicle-mounted howitzers[D]. Nanjing: Nanjing University of Science and Technology, 2008. (in Chinese) [13]朱孙科, 马大为, 于存贵, 等. 多管火箭炮定向管的多目标优化及多属性决策研究[J]. 兵工学报, 2010, 31(11): 1413-1417. ZHU Sunke, MA Dawei, YU Cungui, et al. Study on MRLS direction pipe’s multi-objective optimization and multi-attribute decision making[J]. Acta Armamentarii, 2010, 31(11):1413-1417. (in Chinese) A Parameter Sensitivity Analysis Method Suitable for Complex Non-linear Black-box System DENG Huiyong1, WANG Yan2, HAO Gang1, SUN Haitao1 (1.Ordnance Engineering College, Shijiazhuang050003, Hebei, China;2.Divided Storage of Unit 66442, Yangquan045233, Shanxi, China) Through research on the advantages and disadvantages of main global sensitivity analysis method in the course of solving practical problems, the Dual-parameters Sensitive Analysis method (DGSA) based on mean value and variance of multi local sensitivities in definition domain that was used to access global sensitivity was proposed, while multi-attributes decision-making method was used to calculate the sensitive value by the above two parameters. DGSA method overcomes the defect of global sensitivity accessed by single parameter. Since the distribution patterns of input variable and output response are dispensed with, a credible result can be obtained with less data. As a result, a new method to solve this type of problems is provided. An example was used to verify the validity and credibility. sensitivity analysis; non-linear system; dual-parameters; black-box system 2015-04-01 邓辉咏(1983—),男,讲师,博士,主要从事武器系统仿真与信息化技术研究。E-mail:deng-124@163.com TB114.3 A 1673-6524(2016)01-0012-044 结论
