振动模糊星图的PSF函数估计及复原算法研究*

张　涛，王宏力，陆敬辉，姜　伟

（火箭军工程大学控制工程系，西安710025）

振动模糊星图的PSF函数估计及复原算法研究*

张涛，王宏力*，陆敬辉，姜伟

（火箭军工程大学控制工程系，西安710025）

针对弹体角振动引起的星图成像质量退化的问题，提出了一种基于自适应形态学PSF估计方法。首先通过研究角振动对星点像移的影响得到振动PSF模板，避免将模糊过程简单近似为一维匀速直线运动和一维快速简谐运动得到PSF；其次，为了消除或减弱弹体角振动引起的模糊，提出了一种改进约束条件的最小平方的星图复原算法；最后进行仿真验证，仿真结果表明本文方法能较好的估计随机振动的PSF，提高了模糊星图复原的精度和鲁棒性，复原后的峰值信噪比和结构相似比相比模糊星图分别提高了23.3%和42.6%。

图像处理；PSF估计；形态学；角振动；星图复原

星敏感器作为一种具有高测量精度的空间姿态光学敏感器［1］，可为中远程弹道导弹提高准确的空间方位和姿态基准［2］。对于捷联安装的星敏感器，由于其固连在导弹弹体上，在中制导实时调姿和变轨过程中会产生受迫振动，使得星图模糊，星图信噪比降低，进而影响星体质心提取的精度［3］。因此如何复原振动模糊星图就成为一个亟待解决的问题。

传统的机械式、光学式、电子式像移补偿法可以有效地抑制运动模糊，但存在体积大、成本高、结构复杂、应用不灵活等缺陷，而且难以适应弹体高动态、随机振动造成的模糊［4］。星图复原技术通过对星图进行后期处理消除振动模糊，且成本低，是解决振动模糊星图问题的一个重要途径。

星图复原的关键技术主要有参数识别和复原滤波器设计两项，前者利用不同先验知识获取适当的退化参数，即点扩展函数PSF，后者则根据这些参数估计真实星图［5］。目前，对于PSF的估计，韩礼［4］、谢冰［6］等学者在研究中选用的模糊尺度和方向是通过计算机仿真得到的，实际应用价值不高，且将模糊过程近似为一维匀速直线运动和一维快速简谐运动来处理得到PSF，具有很大的局限性。对于复原滤波器的选择，吴小娟［7］、段小庆［8］等分别引入维纳滤波器和约束最小二乘滤波器，但维纳滤波器工作时会增强低频段中偏高的频率，在视觉上表现为一些不必要的细节增强；而约束最小二乘滤波器工作时在高频区Sn（u，v）/Sf（u，v）取较大的值，噪声较强时复原效果较差。

针对上述分析中PSF估计和复原滤波器选择存在的局限性，本文首先从振动模糊星图本身得到PSF模板，提出了一种适用范围更广的自适应形态学PSF估计方法，可以较好解决随机振动过程中星图退化的先验知识无法获得的难题；其次改进复原方法，提出一种改进约束条件的最小二乘星图复原算法，可以达到更好的复原效果；最后，选取峰值信噪比和结构相似性作为星图复原程度的客观评价参数，对复原效果进行了分析。

1　星图振动PSF估计

1.1基本原理

自适应形态学方法的基本原理是从星敏感器拍摄的星图中估计振动PSF［9］。美国喷气推进实验室的C.C.Liebe提出了星敏感器针孔模型［10］，如图1所示。从成像模型可得知，如果一颗恒星的成像记录下了曝光时间内的光轴的振动模糊信息，那么从星图中恒星的成像就能精确获得振动模糊PSF。

图1中OPxPyP为像平面坐标系，OP为坐标原点，是星敏感器光学系统的光轴与图像传感器感光面的交点，xP轴与yP轴相互垂直，分别平行于感光面的行列方向。OSxSySzS为星敏感器坐标系，原点OS位于星敏感器光学系统的光心，zS轴为光轴指向，垂直于图像传感器的感光面，xS轴、yS轴分别于像平面坐标系的xP轴、yP轴平行，方向按右手定则确定。星敏感器捷联安装在导弹上，其安装方式如图2所示。

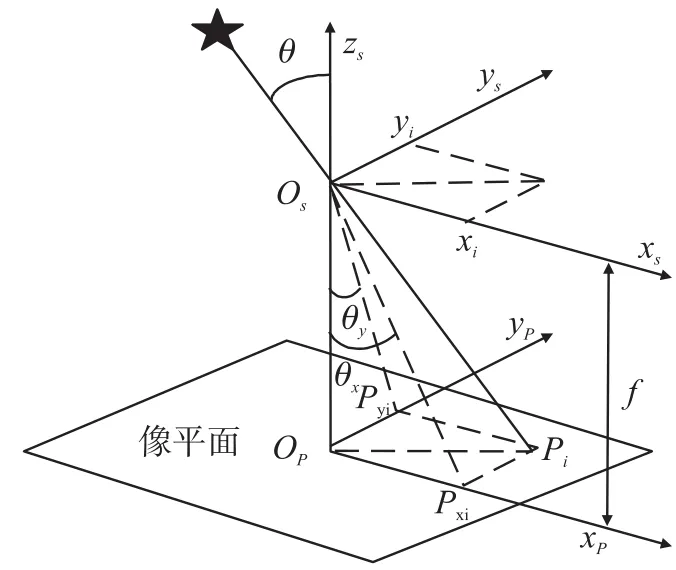
图1　成像模型

图2　安装方式

图2中Obxbybzb为弹体坐标系，星敏感器是安装在弹体坐标系的yb轴上，且xS与zb轴平行、yS轴与xb平行、zS轴与yb轴重合。

由星敏感器的安装方式以及导弹姿态角的定义可知［11］：当导弹偏航振动Δψ时，相当于星敏感器绕坐标系OSxSySzS的yS轴旋转Δψ，这样将使第i颗恒星在像平面上的成像Pi沿像平面坐标系的xP轴方向和yP轴方向移动至。假设像Pi在星敏感器坐标系OSxSySzS中的坐标为（xi，yi，-f），当导弹偏航振动Δψ角后，像Pi和Pi′在星敏感器坐标系OSxSySzS中的坐标分别为（xiψ，yiψ，ziψ）和（x′iψ，y′iψ，z′iψ），则

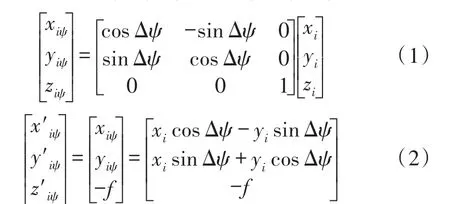
因此，像偏移量为：

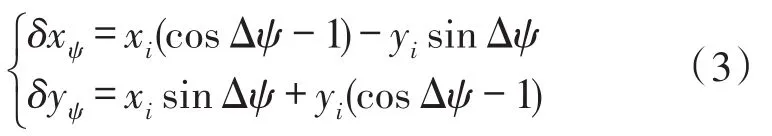
由式（3）可以看出，偏航角振动对星敏感器成像平面上星点的x轴、y轴方向上的坐标均产生影响。

当导弹的俯仰角振动Δφ时，相当于星敏感器绕坐标系OSxSySzS的zS旋转Δφ角度。像Pi和在星敏感器坐标系 OSxSySzS中的坐标分别为（xiφ，yiφ，ziφ）和（x′iφ，y′iφ，z′iφ），则

因此，导弹的俯仰角Δφ引起的像Pi沿像平面坐标系的yP轴方向的像偏移量为：

由式（6）可以看出，俯仰角振动对星点的y轴方向上的坐标产生影响，而对x轴方向上的坐标不产生影响。

类似于俯仰角振动Δφ对像移的影响，可分析得滚动角振动Δγ只对星点的x轴方向上的坐标产生影响，而对y轴方向上的坐标不产生影响，则导弹的滚动角振动Δγ引起的像Pi沿像平面坐标系的xP轴方向的像偏移量为：

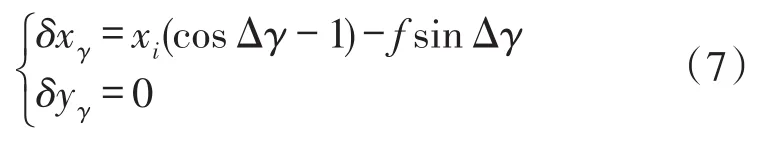
在曝光时间T0时刻，俯仰角抖动为φ（t），偏航角抖动为ψ（t），滚转角抖动为γ（t）时，则偏移量为：

联立式（3）、式（6）、式（7）得：

1.2提取算法

本文通过星敏感器拍摄的星图，用自适应形态学方法提取载体的PSF模板，较好的获得复杂的星图振动PSF。主要流程有星图预处理、星图二值化、形态学滤波（腐蚀和膨胀运算）、振动目标轨迹连通域标记和提取四大部分，提取算法的详细步骤如下：

①星图预处理是对原始星图的数据线性化和灰度均衡化，以便为后续的星图复原提供可靠量化和非灰度畸变的星图信息。

②星图二值化主要用来实现星点振动轨迹与背景噪声分开，选用的方法是动态迭代阈值法［12］，二值化后用四连通判据（星点为凸形目标）去除星图中大量单个或者少数像元构成的噪点。

③利用形态学腐蚀和膨胀运算［13］消除二值化后星像内部可能存在的随机小洞和周边可能存在的凹坑和凸刺，腐蚀运算在去除孤立噪声的同时，星点的振动轨迹能够更好保存下来，膨胀运算可以对腐蚀造成的轨迹失真和断裂进行修补，对断裂区域重新连接，确保振动轨迹所在星图区域的完整。

④形态学滤波后将星图中的连通区域初步确定为候选区并分别进行标记，由于成像噪声、量化噪声等会对PSF模板影响，因此通过比较各个标记窗口尺寸和能量信息，选取尺寸/能量最大的窗口作为振动PSF模板。

2　基于改进约束条件的最小平方复原方法

由文献［6-7］可知，约束最小平方星图复原方法中的二阶微分对星图中的孤立噪声有较好的抑制作用，减小了H（u，v）对噪声的敏感性，但二阶微分对星图本身的细节也有很强的响应，在平滑星图的同时也削弱了星图的细节，基于上述原因，引入Sobel算子对振动模糊星图进行一阶微分处理。因为一阶微分的约束条件将减少星图细节的损失并抑制星图模糊，弥补了单独采用二阶微分的约束最小平方复原算法的不足。算法表达式如式（10）所示：

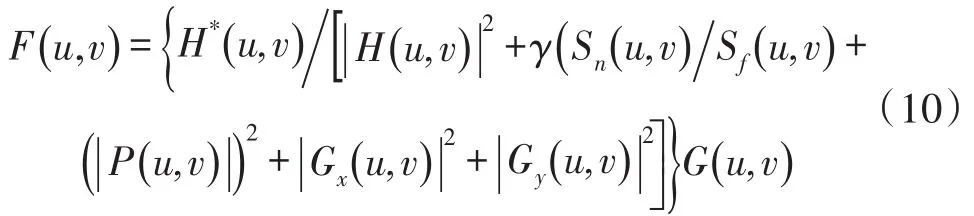
3　复原星图质量评价方法

峰值信噪比PSNR（Peak Signal-to-Noise Ratio）和结构相似比SSIM（Structure Similarity Ratio）是客观评价星图质量最常用的评价标准之一［14］。PSNR 和SSIM的表达式如下：

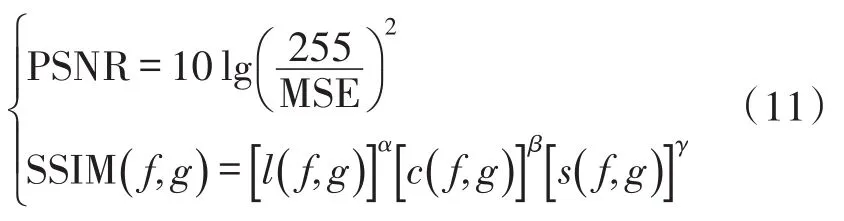
其中 μ、σ和σxy分别为星图的均值、标准差和协方差，C1、C2、C3为正实数常数。

4　实验结果与对比分析

4.1实验参数设定

星敏感器曝光时间为0.005 s，分辨率为1 024× 1 024，视场角为8°×8°，像元大小15 μm，视轴指向为（113°，30°），高斯半径为5 pixel。振动模糊过程中加入均值为0，方差为0.001的高斯白噪声，由于弹体上星敏感器的成像相机信噪比较高，Sn（u，v）/Sf是否精确对复原影响较小，因此k取值为0.001。

4.2仿真实验

首先通过加入振幅为0.005 rad，频率在20 Hz～2 000 Hz之间变化的随机振动对标准星图进行模糊，设定仿真星图帧数为n=25得到星点振动轨迹，然后根据1、2节的PSF提取算法提取模糊星图的PSF，实验结果如图3所示。

图3　PSF提取过程

由图3（f）标记的窗口可知，窗口3尺寸/能量最大，因此选择其作为振动PSF模板。

利用图4提取到的PSF模板，对经过相同振动参数处理的模糊星图进行复原，复原方法选择改进约束条件的最小平方算法，当迭代次数k=87时得到图5，从图5可以看出振动模糊星图得到了很好的复原。

图4　PSF模板

图5　复原星图

此外还进行了对比实验，对比组分别采用了常用的维纳滤波法、最小平方法，由于三种复原方法均能使模糊星图复原的很好，限于篇幅问题，就不将维纳滤波法和最小平方法复原后的星图在本文上体现。由于从主观上无法评价这三种方法哪种方法复原效果更好，因此本文选用峰值信噪比PSNR和结构相似比指数SSIM作为客观评价指标，实验数据统计如表1所示。

表1　实验数据统计

从表1的实验数据可以分析得到：振动会使得星图的峰值信噪比和结构相似比下降，而复原能较好的提高峰值信噪比和结构相似比。维纳滤波法、最小平方法以及本文方法这三种方法复原后得到的SSIM的值相差不大，但本文方法得到的值最高，比模糊星图提高了42.6%；而复原得到的PSNR的值相差较大，比较结果为：维纳滤波法＜最小平方法＜本文方法，本文方法相比模糊星图提高了23.3%。综上可知，本文选用的复原方法优于维纳滤波法和最小平方法。

5　结束语

本文通过研究弹体角振动对星点像移的影响得到载体振动PSF模板，并从模糊星图中自适应估计随机振动的PSF，避免了将模糊过程简单近似为一维匀速直线运动和一维快速简谐运动得到PSF。改进约束条件的最小平方的星图复原算法较好的减弱弹体角振动引起的模糊，这为下一步星图识别以及姿态确定打下基础，对提高星光制导的性能有着重要意义。

［1］陈雪芬，康国华.基于ITSI优选算法的星敏感器导航星库建立［J］.传感技术学报，2014，28（3）：381-386.

［2］孙高飞，张国玉，刘石，等.高精度背景可控星图模拟器设计［J］.红外与激光工程，2015，44（7）：2196-2199.

［3］黄博.临近空间高动态星图仿真技术研究［D］.武汉：华中科技大学，2012.

［4］韩礼，张力军，蔡洪，等.基于维纳滤波的运动模糊星图复原仿真分析［J］.光学技术，2014，40（4）：316-320.

［5］王辉，吴钦章.基于图像质量评价的自动图像复原技术［J］.传感技术学报，2012，25（7）：930-935.

［6］谢冰.基于TDICCD像移分析的PSF估计及图像复原［D］.河北：燕山大学，2005.

［7］吴小娟，王新龙.星图运动模糊及其复原方法［J］.北京航天航空大学学报，2011，37（11）：1338-1342.

［8］段小庆，王宏力.运动模糊图像复原技术在星图中的应用［J］.微计算机信息，2008，24（11）：296-298.

［9］纪峰，李翠，常霞，等.基于改进阈值函数的自适应图像去噪方法［J］.传感技术学报.2014，27（3）：351-354.

［10］Liebe C C.Accuracy Performance of Star Trackers-Atutorial［J］. IEEE Transactions on Aerospace Systems and Electronic System，2002，38（2）：587-589.

［11］王洪涛，罗长州，王渝，等.弹载星敏感器动态测角的分析［J］.现代防御技术，2010，29（1）：37-41.

［12］唐晓强.自适应形态学图像边缘检测算法的研究［D］.新疆：新疆大学，2010.

［13］顾茂松，杨小冈.自适应边缘检测方法的研究［J］.计算机工程，2007，33（5）：185-186.

［14］邓勤.卫星颤振对遥感成像质量影响研究及实验验证［D］.浙江：浙江大学，2013.

张涛（1992-），男，江西上饶人，硕士研究生，主要从事星敏感器测量精度研究；

王宏力（1965-），男，陕西凤翔人，教授，博士，主要研究方向为导航制导与控制、复合制导、天文/惯性导航、故障诊断及可靠性评估，775128700@qq.com。

Research on PSF function Estimation and Restoration Algorithm for Vibration Fuzzy Star Image*

ZHANG Tao，WANG Hongli*，LU Jinghui，JIANG Wei
（Dept of Control Engineering，Rocket Force University of Engineering，Xi’an 710025，China）

This paper aim to solve the problem as to quality degradation of star mapping by adaptive morphology based PSF estimation method.Firstly，a vibration PSF template was obtained through studying the influence of angular vibration on star point displacement，the fuzzy process was avoided from being simply approximate to one-dimensional uniform linear motion and one-dimensional fast simple and harmonic motion，then PSF was obtained；secondly，a star image restoration algorithm of the least square based on improved constraint conditions was proposed to eliminate or weaken the fuzzy caused by angular vibration of the projectile body；finally，simulation verification was made.The result shows that the improved method could better estimate the randomly vibrating PSF and improve the accuracy and robustness of the restoration of fuzzy star image.Compared with the fuzzy star image，the peak signalto-noise ratio and the structure similarity ratio after restoration were improved by 23.3%and 42.6%，respectively.

image processing； PSF estimation； morphology； angular vibration； star map restoration

TP391.41

A

1004-1699（2016）08-1234-05

EEACC：6140；613510.3969/j.issn.1004-1699.2016.08.019

项目来源：陕西省科学技术研究发展基金项目（2014MJ2-6107）

2016-01-19修改日期：2016-03-29