混沌粒子群优化算法在PID参数整定中的应用

张霞

(太原学院，太原 030032)



混沌粒子群优化算法在PID参数整定中的应用

张霞

(太原学院，太原 030032)

针对传统PID参数整定方法和智能PID参数整定方法存在的不足，将粒子群优化算法与混沌理论相结合，提出了基于Logistic映射的混沌粒子群优化算法，并将该算法应用于PID参数的优化整定。结果表明： 该算法能够获得良好的整定效果和收敛特性，从而验证了该算法的可行性和优越性。

粒子群优化算法混沌PID参数整定

Abstracts： In view of shortage of parameter tuning methods for traditional and intelligent PID， chaos particle swarm optimization algorithms based on Logistic mapping is proposed with combination of particle swarm optimization algorithm and chaos theory， and is applied in PID parameter optimization and tuning. The results show good setting effect and astringent properties can be obtained with the algorithm. The feasibility and superiority are verified.

在工业生产中，通常用闭环控制方式来控制温度、压力、流量等连续变化的模拟量。由于PID控制器结构简单，控制效果好，参数调整方便，容易实现，有较强的灵活性和适应性，因而在工业控制领域中，PID控制为使用最多的闭环控制方式。PID参数的整定是PID控制器设计的关键，但是PID参数整定的过程是复杂、繁琐的。在实际应用中，如果PID参数整定得不好，系统的动静态性能达不到要求，甚至会使系统不能稳定运行。

传统的PID参数整定方法存在很多局限，很难满足对控制品质要求较高的场合。例如，Ziegler-Nichols整定算法(Z-N)不适用于时间滞后相对大的对象；Cohen-Coon整定算法不适用于衰减比太小的闭环系统。目前出现的智能参数整定方法也存在很多不足，很难实现参数的最优整定。例如，神经网络算法在参数选择时没有系统的方法；遗传算法的计算量大，解码过程繁琐[1]。文中引入基于Logistic映射的混沌粒子群优化算法(CPSO)对PID控制器的参数进行整定，通过采用Matlab软件仿真，结果表明了该算法能够获得满意的优化整定效果。

1　混沌粒子群优化算法

粒子群优化算法(PSO)[2]是演化计算领域中一个新的分支，它的概念源于对鸟群运动行为的研究，通过研究个体之间的协作来寻求最优解，是一种基于种群寻优的演化计算技术。与其他进化算法相比，粒子群优化算法的概念更简单易懂，在计算机上便可实现，并且可以获得较好的寻优特性，因而它的应用范围不断扩大，得到了迅速发展。混沌是一种普遍的非线性现象，既存在确定性，也存在随机性，是客观存在的一种矛盾统一体。文中将混沌引入到粒子群优化算法，利用混沌的随机性、遍历性等特点对系统进行优化搜索，可以避免粒子群优化算法存在的过早收敛问题，从而提高算法精度。

根据控制器的参数与系统动静态性能之间的定性关系，可以利用CPSO来整定PID控制器的3个主要参数。利用CPSO整定控制器的PID参数，本质上是在一定目标函数上的参数寻优计算。性能指标是对控制系统进行总体评价的准则，它反映了控制系统的调节品质，文中采用时间绝对偏差乘积积分函数(ITAE)的倒数来衡量PID控制系统的性能，如下式所示：

(1)

式中：J——粒子适应度值。

文中采用Matlab软件仿真实现，基于CPSO的PID控制器参数整定，具体步骤如下：

1) 根据Z-N参数整定公式(见表1所列)确定PID控制器参数KP， KI， KD的取值范围，同时对算法参数赋值，设定粒子群规模数popsize，变量的取值范围[xmin， j， xmax， j]，最大迭代次数MaxIter。

表1　Z-N参数整定公式

2) 初始化粒子群。根据混沌搜索，赋N个具有微小差异的初值，产生N个混沌变量。文中利用Logistic映射，生成含有N(N>popsize)个粒子的种群，即产生N个混沌变量，Logistic映射迭代方程如下所示：

(2)

式中： μ——控制参数，μ=4；j， i， zj——混沌变量的序号、粒子群序号、混沌变量。

3) 将N个混沌变量分别引入到下式所示的优化变量中，载波映射对应的混沌区间：

(3)

j=1， 2， …， D

4) 计算每个粒子的个体适应度值。将每个粒子的目前最优值记为pbest，种群中适应度最优值记为gbest。

5) 更新粒子速度和位置，重新计算每个粒子的个体适应度值。若所计算结果优于原来的粒子个体最优值，便更新当前个体最优值pbest，并判断是否更新群体最优值gbest。

6) 如果当前迭代次数不小于最大迭代次数的2/3倍，则在当前群体最优值中附加1个小幅度的混沌扰动量，然后载波映射对应的混沌区间，继续进行迭代。

7) 判断是否达到预先设定的迭代次数。若满足算法终止条件，则输出PID控制器参数的3个最优值；否则，执行第5步。

2　仿真实例及结果

为了便于比较，文中采用不同优化算法，通过调用Matlab的控制系统工具箱，对系统的PID参数进行了整定。文中选取控制器的传递函数[3]： G(s)=e-0.5s/(s+1)2。

文中利用Simulink对控制系统进行建模和仿真，仿真模型如图1所示。在该仿真模型中设置PID的3个参数KP， KI， KD为工作空间中的变量，延时环节设置为0.5。CPSO的具体参数设置： 种群粒子数N=30；最大迭代次数MaxIter=100；惯性权重随迭代次数从ωmax=0.9递减到ωmin=0.4；加速常数c1=c2=2。

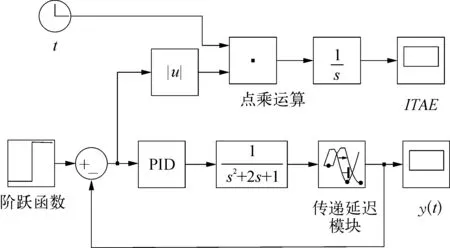
图1　PID仿真模型

为了表明算法的有效性和可行性，将CPSO与传统的Z-N整定算法进行了比较，同时与改进后的PSO，遗传算法GA进行了对比。采用不同整定方法得到的参数整定结果见表2所列，同时得到对应的系统单位阶跃响应曲线如图2所示。

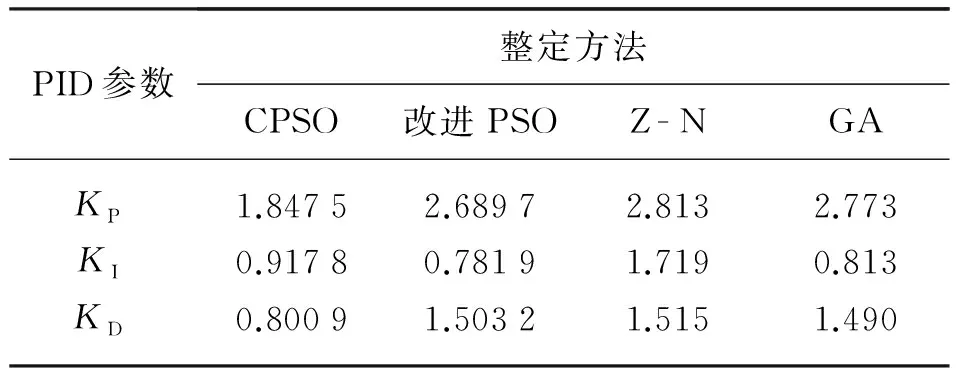
表2　不同整定方法对应参数

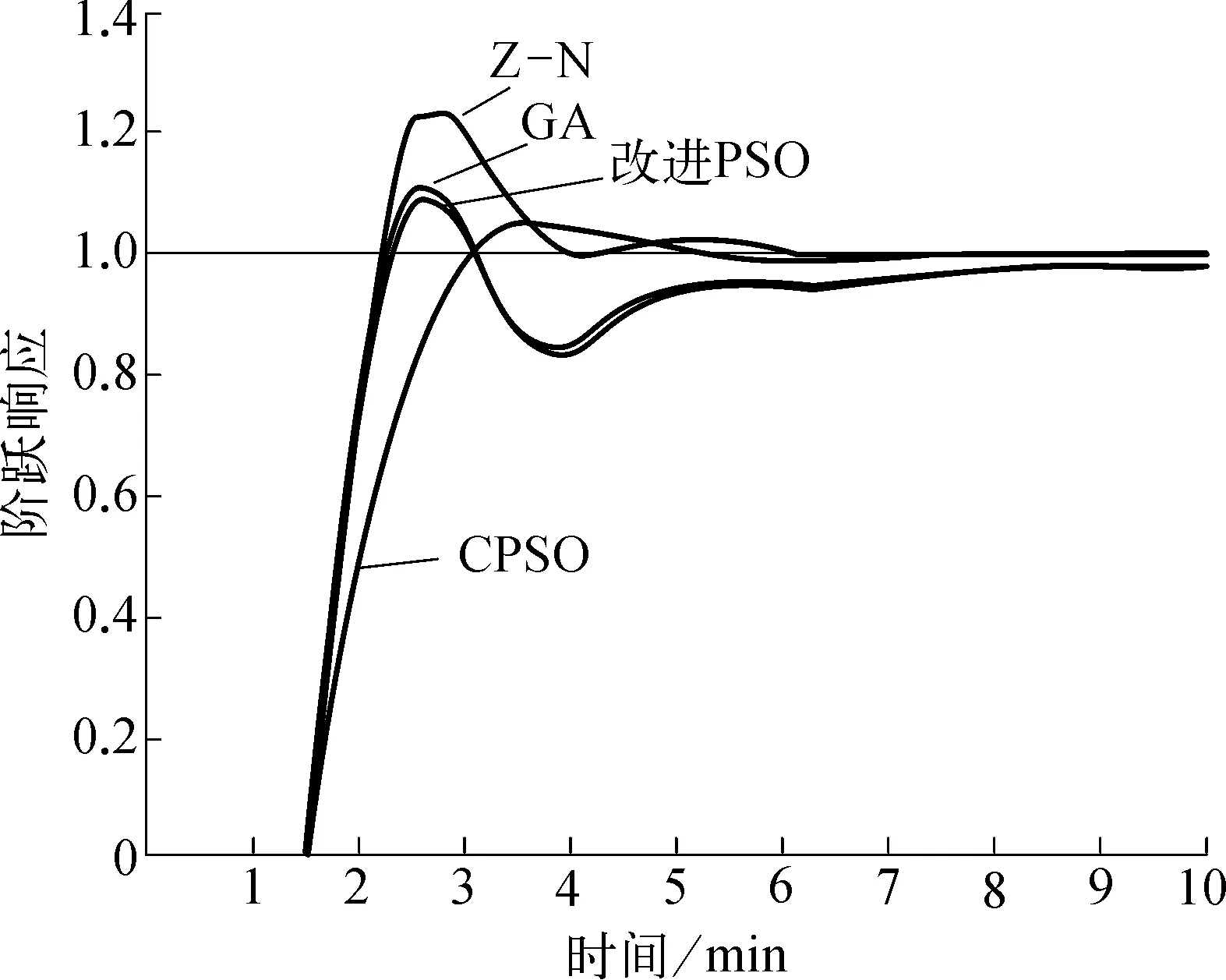
图2　不同整定方法对应的单位阶跃响应曲线

由表2和图2可知，CPSO获得了良好的整定效果和收敛特性。CPSO相比于传统的Z-N，改进后的PSO和GA，得到的控制曲线更加平稳，没有反向超调，最大超调量小，振荡次数少，并且能够在较小的温差范围内跟踪到设定值。从图2中能够看到在优化时间上，CPSO没有体现出明显的优越性。但总体来说，CPSO优化结果良好，达到了控制系统稳、准、快的要求，从而验证了该算法的可行性和优越性。

[1]GOREZ R. A Survey of PID Auto-tuning Methods[J]. Journal A， 1997， 38(01)： 3-10.

[2]ZhANG C S， SUN J G. An Alternate Two Phases Particle Swarm Optimization Algorithm for Flow Shop Scheduling Problem [J]. Expert Systems with Applications， 2009， 36(03)： 5162-5167.

[3]JIANG Y， HU T S， HUANG C C， et al. An Improved Particle Swarm Optimization Algorithm[J]. Applied Mathematics and Computation， 2007， 193(01)： 231-239.

[4]李爱国，谭征.粒子群优化算法[J].计算机工程与应用，2002，38(21)： 1-3.

[5]周驰，高海兵，高亮，等.粒子群优化算法[J].计算机应用研究，2003，12(01)： 7-11.

[6]CARROLL L， ECORA M P. Synchronizing Chaotic Circuits IEEE Trans[J]. CAS， 1991， 38(04)： 453-456.

[7]PECORA M， CARROLL L. Driving Systems with Chaotic Signals[J]. Phys. Rev. A， 1991， 44(04)： 2374-2381.

[8]詹姆斯.格莱克.混沌开创新科学[M].上海： 上海译文出版社，1990.

[9]安凤栓，常俊林，苏丕朝，等.基于改进粒子群优化算法的PID控制器参数优化[J].工矿自动化，2010(05)： 54-57.

[10]ZIEGLER J G， NICHOLS N B. Optimum Settings for Automatic Controllers[J]. Journal of Dynamic System Measurement， and Control， 1993， 115(2B)： 220-222.

Application of Chaos Particle Swarm Optimization Algorithm in PID Parameter Tuning

Zhang Xia

(Taiyuan College， Taiyuan， 030032， China)

particle swarm optimization algorithm；chaos；PID parameter tuning

张霞(1986—)，女，山西大同人，硕士学位，现就职于太原学院，任助教。

TP273

A

1007-7324(2016)04-0032-02

稿件收到日期： 2016-03-25。