矿山微震定位子台网的分布对定位精度的影响

陈法兵

（1.煤炭科学研究总院开采研究分院，北京100013；2.天地科技股份有限公司开采设计事业部，北京100013）



矿山微震定位子台网的分布对定位精度的影响

陈法兵1，2

（1.煤炭科学研究总院开采研究分院，北京100013；2.天地科技股份有限公司开采设计事业部，北京100013）

台站数目、最大空隙角、近台震中距和台站高差是微震定位子台网的4个关键参数。在微震定位理论和数值仿真实验研究的基础上，分析了这4个关键参数对定位精度的影响。利用千秋煤矿现场爆破事件的数据，分析了4个参数与平面定位精度和垂直定位精度的关系，最终得出微震定位子台网的分布对定位精度的影响：理论上参与定位的台站数目越多定位精度越高，但是台站数目的增多也必然会导致问题通道数目的增多，因此台站数目以5～9个为宜；垂直离散度系数K可以反映台网垂向分布的优劣，K值越大，垂直定位误差越小；台网最大空隙角越小，震中定位精度越高；近台震中距决定了震源深度的定位精度，因此必须保证最近台站参与定位计算。

微震定位子台网；定位精度；台站数目；最大空隙角；近台震中距；台站高差

近年来随着煤矿开采深度和强度的急剧增大，冲击地压灾害愈演愈烈。在这样的背景下，微震监测技术被引入中国，并获得了蓬勃发展，现已经成为防冲治灾不可或缺的重要手段之一［1-4］。

震源的定位精度是衡量微震台网监测质量的重要指标，在很大程度上决定了微震监测的效果［5］。影响定位精度的因素有很多，其中台网布置是关键［6-10］。合理的台网布置可以提高定位精度，否则会造成震源求解方程出现病态或死局，引起较大误差甚至无解［11］。

震源定位算法要求至少有4个台站接收到清晰P波波形才可以对此震源进行精确定位。但现实中，尤其是大能量事件，收到有效波形的台站数目大于4个。由于并不是参与定位台站数目越多，定位精度就越高，所以面临一个定位子台网的选取问题。从所有有效台站中选取用于震源定位的台站组合就叫定位子台网组合。定位子台网组合的分布主要取决于4个因素:台站数目、最大空隙角、近台震中距和台站高差。定位子台网的选取决定了震源的定位精度，因此定位子台网的选取方法对微震监测具有重要的意义［12］。

季爱东等［13］利用山东台网的地震数据研究了定位子台网的选取原则，认为地震速报时选择4～9个分布相对合理的定位子台网参加定位，结果较好，使用水平误差估计定位结果质量比较适合，但是研究是基于地震波形，对煤矿微震监测借鉴意义不大。巩思园［14］根据煤矿实际条件和震动波传播特点，建立了最优通道个数的确定原则，研究认为在台网布设较优时，6个通道就可以保证震源的定位精度，但是研究只是考虑了台站数目对定位精度的影响。

基于以上存在的问题，本文利用数值仿真模拟分别研究了台站数目、最大空隙角、近台震中距和台站高差对定位子台网定位精度的影响，在此基础上，分析了千秋煤矿井下定点爆破的微震数据，得出了4个因素与定位误差的相互关系。

1　微震定位理论

煤矿井下震动波形包括两种:P波和S波，P波速度较快，为初至波，波形起振点较为清晰，因此选择P波进行定位。一般假设煤岩体为各向同性介质，建网之后，利用定点爆破的方式进行波速校核，并给定一个平均波速vP。第i个台站的到时ti可由（1）式描述:

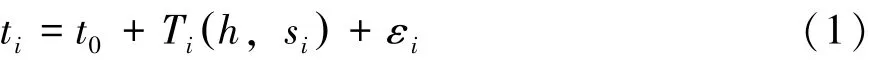
式中，t0为微震事件的发震时刻；h=（x0，y0，z0）和si=（xi，yi，zi）分别为震源和第i个微震台站的笛卡尔坐标；εi为第i个台站的到时误差，i=1，…，n，假设所有台站的到时读数误差均符合正态分布ε～N（0，σ2I），I为单位矩阵，σ为随机误差的方差［15］。

对于均匀和各向同性速度模型，自震源h到第i个台站的走时Ti为:

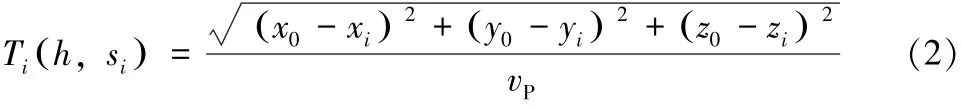
式（2）有t0，x0，y0，z04个未知数，要解此方程至少需要4个台站的数据。震源参数t0和h=（x0，y0，z0）可以通过以下函数的最小值来估算:

式中，θ=（t0，x0，y0，z0），式（3）为超静定方程，需要用最小二乘估计进行求解。使式（3）取得最小值的θ就是震源参数的最优解。

2　数值仿真试验研究

联立式（1）和式（4）可得:

使用矩阵表示如下:

A为（n×4）阶的偏微分矩阵，等于

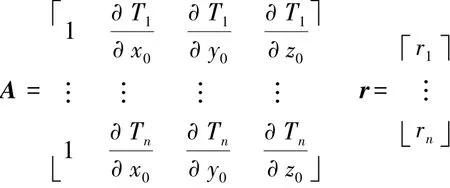
数值仿真采用D值最优化实验方法，D值最佳原则基于下列讨论。

参数θ的置信椭球体用下式表示:

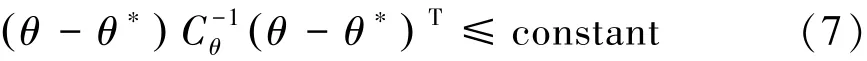
式中，constant是一个来自 k2n-4分布的适当的数值。此式表达了在某一置信水平下θ∗的分布特征。这个椭球体的体积与成比例。D值最佳准则就是通过最小化尽可能减小椭球体的体积，从而使震源参数的最小二乘估计达到最优。达到最小时的微震台站布置就是D值最佳布置［16］。

参数θ的协方差矩阵Cθ=σ2（ATA）-1，定义震中位置标准差为平面圆的半径，该圆的面积等于在（x0，y0）处标准误差椭圆的面积。由于椭圆的两个轴对应协方差矩阵子矩阵的特征值（λx，λy），由此可知震中位置标准差为:

00

同理，可知震源位置标准差为:

2.1台站数目

分别选取4个、5个、6个、7个台站的网络进行模拟，模拟矿井范围为X:-2000～2000m，Y:-2000～2000m，假设平均波速为4000m/s。震中定位误差云图如图1所示，图中实心圆为监测台站，均位于以原点为圆心，半径为1500m的圆上。

把震中定位误差小于20m的区域面积S0占模拟矿井总面积S的比值L作为衡量优劣的标准，即

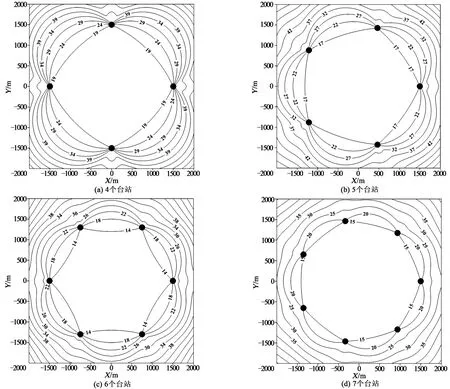
图1　震中定位误差

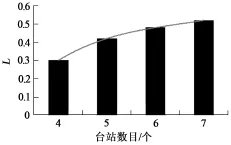
图2　L变化柱状

随着台站数目的增多，L的变化如图2所示。随着台站数目的增多，S0逐渐增大，但是增幅逐渐减小，表明台站数目的增多可以提高定位精度，但是增加到一定程度之后，定位效果增加不显著。

2.2最大空隙角

台网最大空隙角θ是指震中和台站各连线之间的最大夹角。最大空隙角可以反映子台网对于震源分布的均匀性［7，17］，如图3所示。

图3　最大空隙角示意

把原点作为研究监测点，台网最大空隙角分别布置成60°，120°，180°和240°。全矿范围的震中误差云图如图4所示。

图4　震中定位误差

随着最大空隙角的增大，原点的震中定位误差逐渐增大，而且增速变快，如图5所示。可以得出结论，某点的最大空隙角越小，其定位精度就越高。当台站能从四象限包围震中，即θ≤90°，分布最佳，震中位置的测定误差最小；当θ＞180°时，台站都偏于震中一侧，观测效果不好。因此最佳的台网布置应尽量使监测工作面处在θ＜90°区域内。

图5　原点震中误差

2.3台站高差

台网的水平分布决定了震中的定位精度，台网的垂向分布决定了震源深度的定位精度［18］。假设某台网包含n个台站，第i个台站的z坐标为zi，工作面煤层平均标高为z0，台站与煤层的高差Δzi=zi-z0，则所有台站的Δzi组成一个集合S=｛Δzi。定义垂直离散度系数K，如式（12）所示。

式中，Var（ Δzi）为集合S的方差；Max（ Δzi）为Δzi的最大值；Min（ Δzi）为Δzi的最小值。系数K可以评估台站垂向布置的优劣，K值越大表明台站垂向布置越优。

分别选取最大高差为±200m（K=8），±400m（K=64）和±600m（K=216）3种情况进行模拟，模拟结果如图6所示。

把震源Z值定位误差小于20m的区域面积S0占模拟矿井总面积S的比值L作为衡量优劣的标准，L值的变化如图7所示。可见，随着K值的变大，L值呈指数幂急剧升高，证明K值越大，震源Z值的定位效果越好。

2.4近台震中距

定位子台网中离震源最近的台站与震源的距离称为近台震中距。由于在进行震源定位时，震源深度和发震时刻具有相关性，两者之间存在折衷计算，所以震源深度误差较大［19］。国家地震局 《地震目录与地震观测报告编报规范》明确要求近台震中距必须小于50km才认为台网所定地震震源深度有效。只有当震中距小于约1～2倍震源深度时，基于走时方法确定的震源深度才有较高的精度。

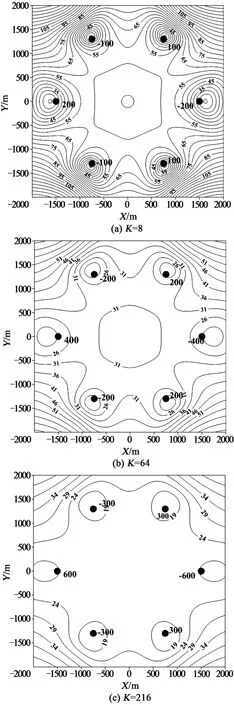
图6　震源Z值定位误差

由于走时与震源参数的关系通常是非线性的，所以至少存在一个极小的拟合函数［20］。如图8所示，如果初始值选在离真实震源较近的θ1点，则迭代结果可以得到全局极小值θ0，也即最佳精确解。如果初始值选在离震源较远的θ2点，则震源计算的迭代结果为θ∗，只是局部极小点，并不是全局最优解。在进行震源计算时，系统默认最近台站坐标为震源求解的初始值，因此最近台站距离震源较远，会使迭代不稳定甚至发散，导致震源定位误差较大甚至无解。

图7　L变化柱状图

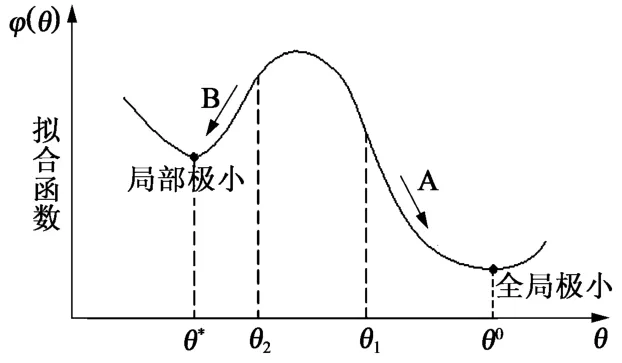
图8 初始值对定位结果的影响

图9为某矿近台震中距云图，图10为基于广义逆的奇异值分解法计算出的震源深度定位误差，可见两图具有很好的相关性，很好地验证了近台震中距与震源深度定位误差的相关关系。

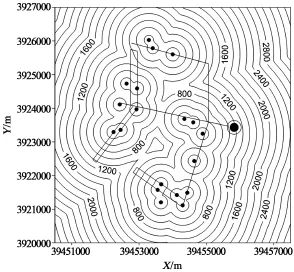
图9　近台震中距云图

3　煤矿井下定点爆破微震数据分析

千秋煤矿井下共安装15个拾震器，在不同位置进行13次定点放炮试验。拾震器布置和放炮点如图11所示，放炮点坐标如表1所示，爆破波形如图12所示。对13个爆破事件，分别在不同台站组合情况下计算定位结果，然后与真实放炮位置对比得出定位误差。通过误差值来判断子台网的台站数目、最大空隙角和近台震中距对定位精度的影响。

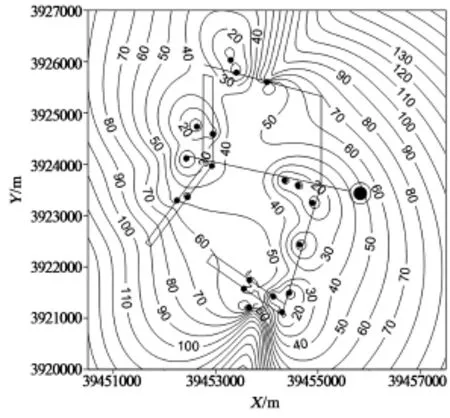
图10　震源深度定位误差

图11　千秋煤矿微震监测台站和定点放炮位置

表1　爆破点坐标

3.1参与定位的台站数目

图12　爆破波形

理论上参与定位台站数目越多，提供的信息越丰富，定位精度就越高，而且参与定位台站数目越多，拾震器对震源的包络就越好，从而抵消了一部分由于人工初至拾取的随机性和速度模型不准确造成的误差。适当增加定位台站数目可以提高震源的定位精度并能在一定程度上保证定位结果的稳定性，如图13（a）所示，从11个台站定位开始，震中和震源定位精度趋于稳定，图13（b）中从12个台站定位开始，震中和震源定位精度趋于稳定。但并不是参与定位台站数目越多，定位精度就越高，因为台站数目的增加也不可避免地增大了问题波形出现的概率，因此参与定位台站数与定位精度并不一定成正比。对13号爆破事件不剔除问题波形，按到时排序从4个台站开始由近及远逐渐增加定位台站数，震中和震源定位误差的变化如图14所示。最近4个台站定位误差较高，从5到8个台站，定位误差一直保持较低水平。从9个台站开始，定位误差逐渐升高。因为距离震源较远的台站收到的震动波形传播的距离较长，经过的采空区和地质不连续带较多，波形的衰减和相变较严重，导致波形出现问题的可能性较大，这种问题波形会导致初至拾取不准确，继而影响定位精度。因此必须剔除这些波形有问题的台站，尤其是那些远台问题波形。

图13　定位误差与参与定位台站数的关系

图14　13号爆破点定位误差与定位台站数的关系

由图13，图14可知震源误差均大于震中误差。震中和震源误差曲线的高度相关性表明震源深度误差随定位台站数的增多，变化不大。即定位子台网台站数目的增多无法提高震源深度的定位精度。

3.2台网最大空隙角

通过对定点放炮事件的定位分析，得到如图15所示散点图。可见最大空隙角与震中定位误差基本呈正相关关系。因此在微震台网建网前就必须合理制定台网分布方案，使工作面开采的整个过程都处在台站的包络范围内，尽量降低最大空隙角，保证定位精度。

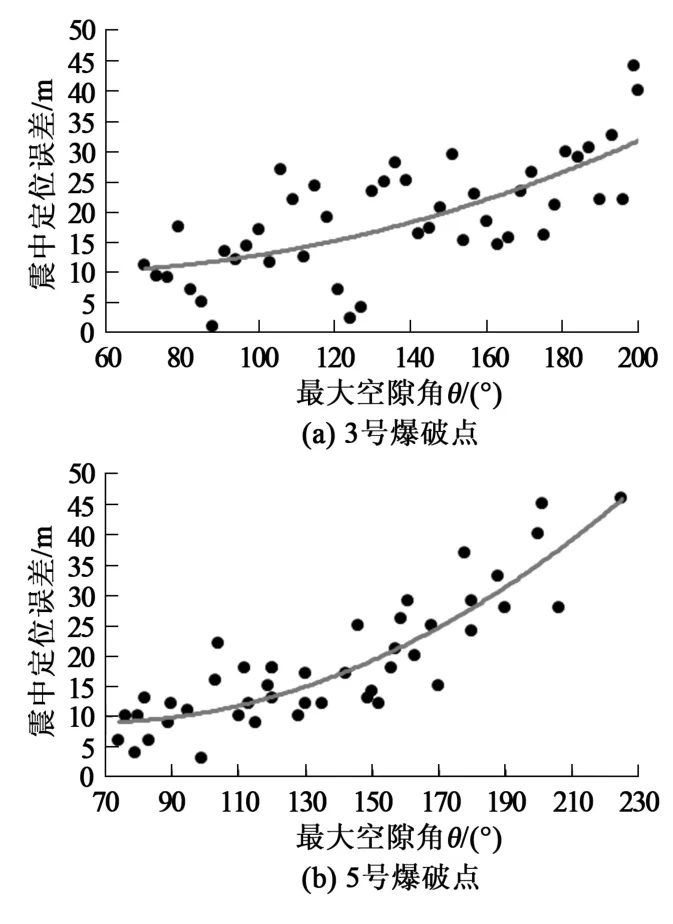
图15　最大空隙角与震中定位误差关系

参与定位台站数的增加同时会大大降低最大空隙角。因此参与定位台站数目不能太少，在保证台站波形没问题的前提下适当增加台站数目可以有效降低最大空隙角，降低定位误差。从定位算法的角度来说，增加参与定位的台站数目和降低最大空隙角都会降低震源求解非线性方程组协方差矩阵的奇异性，从而提高震源求解迭代过程收敛的稳健性［21］。

3.3台站高差

统计分析了3号爆破和10号爆破的微震数据，得出K值与Z值误差的散点图，如图16所示。可知Z值定位误差随K值增大而减小，K值越小，定位误差散点分布越发散。K值为0时，无法对震源Z值进行定位。

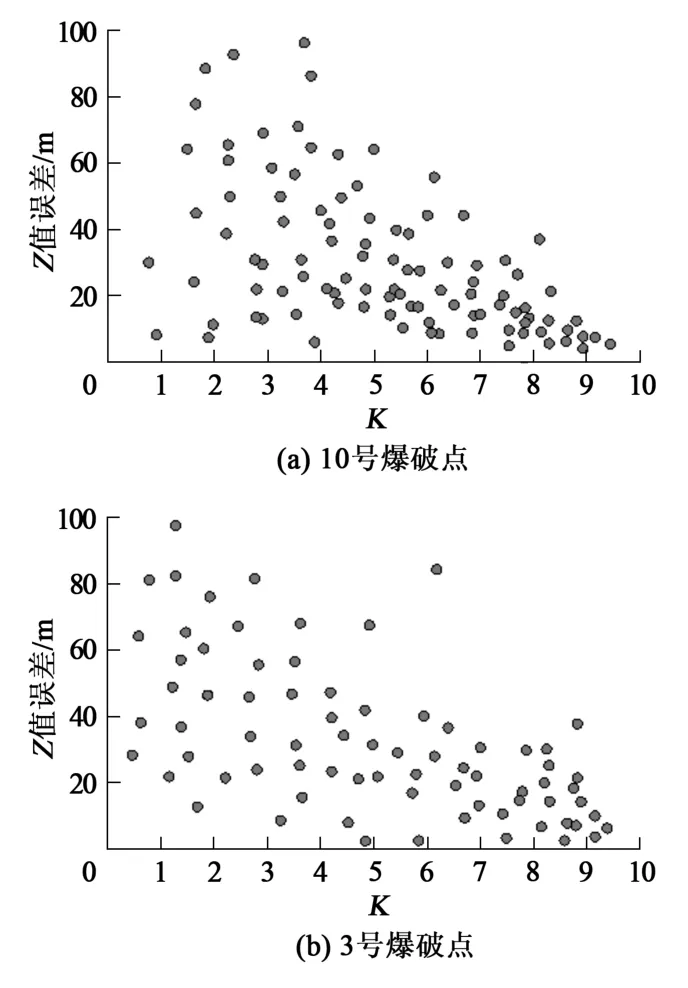
图16　K值与Z值误差的关系

3.4近台震中距

图17统计了近台震中距与定位误差的关系。可知震源误差和震源深度误差随近台震中距的增大有逐渐增大的趋势。震中定位误差与近台震中距无明显相关性。图18所示为8号爆破近台走时与震源深度误差随定位台站数的变化曲线，可以看出震源深度误差与近台震中距有很强的相关性。因此必须保证参与定位的台站之中至少有一个与震源靠近，才能确保震源定位的精确性。

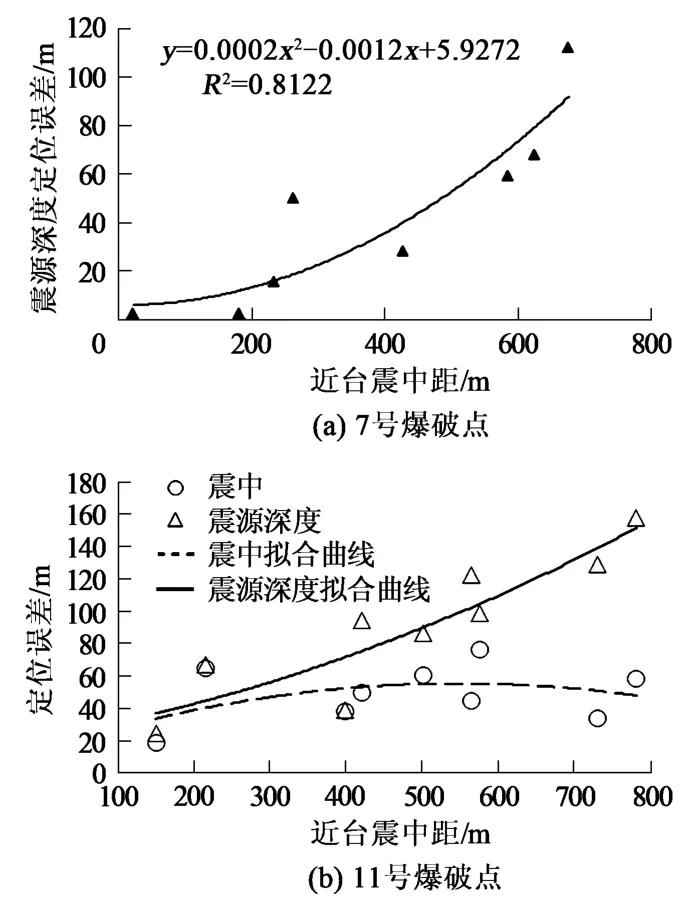
图17　近台震中距与定位误差关系

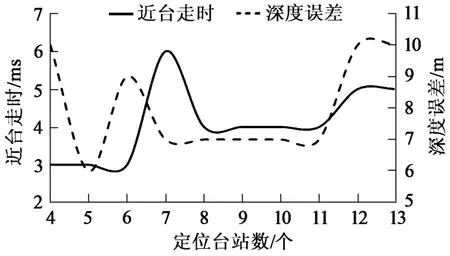
图18　8号爆破近台走时与深度误差的关系

最佳的微震台网布置要保证重点监测工作面处于台站数目、最大空隙角、近台震中距和台站高差4个参数的最优值覆盖区域，从而使震中定位精度和震源深度定位精度都能达到最佳，保证微震监测取得最佳效果。

4　结 论

（1）理论上，参与定位的台站数目越多定位精度越高，但是台站数目的增多也必然会导致问题通道数目的增多，因此台站数目以5～9个为宜。台站数目的增多会导致其他参数的变化，因此分析结果又有一定的离散性。

（2）垂直离散度系数K可以反映台网垂向布置的优劣:K值越大，垂直定位误差越小。

（3）台网最大空隙角越小，台站对重点监测区域的包络效果越好，震中定位精度越高。台站数目的增多会大幅降低最大空隙角。

（4）近台震中距决定了震源深度定位计算的初始值，对震源深度定位误差影响很大，因此最近台站参与定位才能保证震源深度定位结果的可靠性。

［1］夏永学，蓝 航，魏向志.基于微震和地音监测的冲击危险性综合评价技术研究［J］.煤炭学报，2011，36（2）:358-364.

［2］姜福兴，杨淑华，成云海，等.煤矿冲击地压的微地震监测研究［J］.地球物理学报，2006，49（5）:1511-1516.

［3］曹安业，窦林名，秦玉红，等.微震监测冲击矿压技术成果及其展望［J］.煤矿开采，2007，12（1）:20-24.

［4］杨承祥，罗周全，詹礼忠，等.基于微震监测技术的深井开采地压活动规律研究［J］.岩石力学与工程学报，2007，26（4）:818-824.

［5］邹振轩，李金龙，俞铁宏，等.浙江数字地震台网监测能力评估［A］.华东六省一市地学科技论文集［C］.2011.

［6］Kijko，An Algorithm for the Optimum Distribution of a Regional Seismic Network.Pure Appl.Geophys.115，999-1009（1977）.

［7］赵英萍，高景春，刘 丽，等.定位子台网的选取对定位结果影响研究［J］.地震，2006，26（4）:37-44.

［8］姜长宁.江苏数字地震台网地震定位能力分析［J］.地震学刊，2001，21（2）:1-5.

［9］郭 飙.首都圈数字地震台网的微震定位实验［J］.地震地质，2002，24（3）:453-460.

［10］焦远碧，吴开统，杨满栋.我国地震台网监测能力及台网观测条件质量评定［J］.中国地震，1990，6（4）:1-7.

［11］李学政，雷 军.近场爆炸地震优化定位方法研究［J］.地震学报，2001，23（3）:328-333.

［12］许俊奇.测震台网布局对震源参数精度的影响［J］.地震地磁观测与研究，1988（3）:1-7.

［13］季爱东，钟普浴.山东数字地震台网定位子台网选取对定位结果的影响［J］.地震地磁观测与研究，2011，32（4）: 62-66.

［14］巩思园，窦林名，曹安业，等.煤矿微震监测台网优化布设研究［J］.地球物理学报，2010，53（2）:457-465.

［15］朱介寿.地震学中的计算方法［M］.北京:地震出版社，1988.

［16］Slawomir Jerzy Gibowicz，Andrzej Kijko.矿山地震学引论［M］.北京:地震出版社，1998.

［17］中国科学院地球物理研究所.近震分析［M］.北京:地震出版社，1977.

［18］Mendecki A J.Seismic Monitoring inMines［M］.London: Chapman and Hall Press，1997.

［19］罗 艳，曾祥方，倪四道.震源深度测定方法研究进展［J］.地球物理学进展，2013，28（5）:2309-2321.

［20］李汯鑑，S.W.斯图尔特.微震台网的原理和应用［M］.北京:地震出版社，1984.

［21］朱元清，赵仲和.提高地震定位精度新方法的研究［J］.地震地磁观测与研究，1997，18（5）:59-67.

［责任编辑：潘俊锋］

Influence of Mine Microseism Location Sub Network Distribution to Positioning Precision

CHEN Fa-bing1，2
（1.Institute of Mining，China Coal Research Institute，Beijing 100013，China；2.Coal Mining&Designing Department，Tiandi Science&Technology Co.，Ltd.，Beijing 100013，China）

The four key parameters of microseism location sub network are station number，the maximal gap angle，nearly station epicentral distance and station height difference，on the basis of microseism location theory and numerical simulation experiment，the influence that the four key parameters to location precision was analyzed.The relation between the four parameters to planar location precision and vertical location precision was analyzed based on the data of explode incident of Qianqiu coal mine.Then influence of microseism location sub network distribution to location precision was drawn out，which is the more station number the more location precision in theory，but the problematic channel will increase with station number increase，so the rational station number is 5～9.The advantage and disadvantage of network vertical distribution could be reflected by vertical variation coefficient，the vertical location error decrease with K increase，the smallest gap angle the largest microseim location precision，the location precision of microseism source was depend by nearly station epicentral distance，so the closest station must included in location calculation.

microseim location sub network；location precision；station number；the maximal gap angle；nearly station epicentral distance；station height difference

TD326

A

1006-6225（2016）04-0107-08

2016-01-13

［DOI］10.13532/j.cnki.cn11-3677/td.2016.04.028

国家自然科学基金资助（51204097；51304118）

陈法兵（1985-），男，山东泰安人，工程师，主要从事煤矿冲击地压灾害防治与微震监测技术研究。

［引用格式］陈法兵.矿山微震定位子台网的分布对定位精度的影响［J］.煤矿开采，2016，21（4）：107-114.