吉伯阻尼磁化率张量的矢量解法
2016-09-18朱瑞华
朱瑞华,于 淼
(牡丹江师范学院物理与电子工程学院,黑龙江 牡丹江 175012)
吉伯阻尼磁化率张量的矢量解法
朱瑞华,于 淼
(牡丹江师范学院物理与电子工程学院,黑龙江 牡丹江 175012)
在一阶近似条件下,通过矢量运算求解了含有吉伯阻尼项的朗道-栗夫席兹方程,得出了吉伯阻尼磁化率张量与无阻尼磁化率张量之间的满足的关系式。该关系式对不同的旋磁材料都有效。此后利用该关系式,从铁磁体的无阻尼磁化率张量出发导出了铁磁体的吉伯阻尼磁化率张量。
朗道-栗夫席兹方程;吉伯阻尼;磁化率张量
1935年,朗道和栗弗席兹在研究铁磁体磁导率的色散理论中提出著名的磁化进动方程:

该方程即朗道-栗弗席兹方程,又称为铁磁链方程[1,2,3]。其中M为磁化强度;为真空磁导率;为有效场;为旋磁比,通常小于零;为阻尼系数。该方程可以描述磁化绕着做进动的过程。该方程自带的阻尼项为:
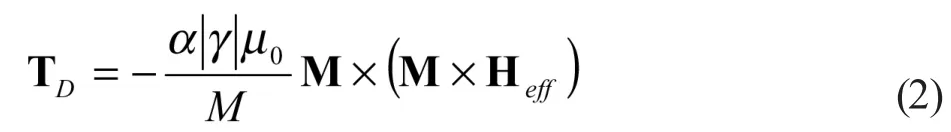
1955年,吉伯简化了(2)式的阻尼形式[4,5]。将(2)式中的使用式来代替,这样得到吉伯阻尼项:

添加(3)式阻尼项后的进动方程常常称为朗道-栗夫席兹-吉伯方程,也称为含有吉伯阻尼项的朗道-栗夫席兹方程。其形式如下:
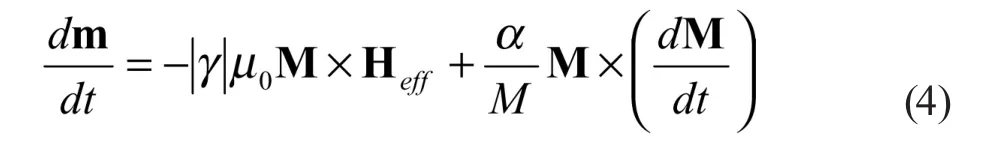
(4)式是磁偶极模式研究的一个基本方程。在求解该方程时,通常将该方程分解成为分量的形式。在本文中我们尝试使用矢量运算来求解该方程,由此得出旋磁的磁化率张量。
1 吉伯尼磁化张量的统一形式
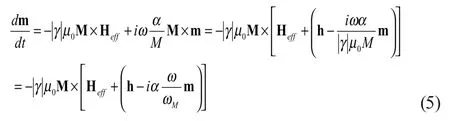

将(6)式移项整理后得到,


(8)式是本文得出的核心内容,它将吉伯阻尼磁化张量表示为无阻尼的磁化张量的函数。由于我们在推导的过程中没有对无阻尼磁化率张量的具体形式做出任何限制,因此(8)式适用于各种情况的旋磁材料。具体计算有阻尼磁化率张量,只需将各种形式的无阻尼磁化率张量带入即可。对(8)式还可以进一步进行分母有理化,从而将有阻尼磁化率张量的实部与虚部分开。

2 铁磁体的吉伯阻尼磁化率张量
以铁磁体为例,从其无阻尼磁化率张量出发来计算其尼磁化率张量。铁磁体的无阻尼磁化率进动张量表示为[4]:
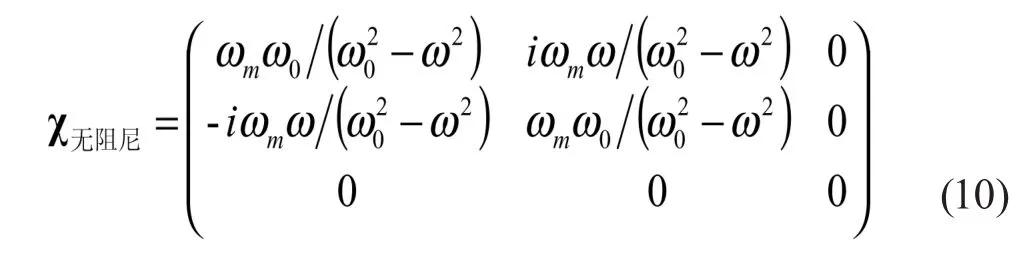
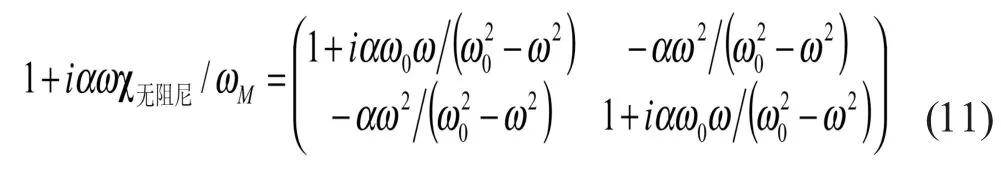
该矩阵的逆矩阵表示为:

使用(8)式进行矩阵乘法运算得到:
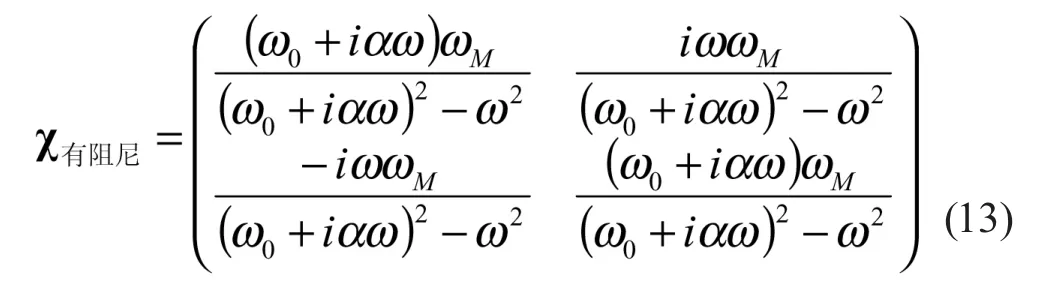
考虑到z方向磁化率为零,磁化率的完整形式可以写成为:

其中:
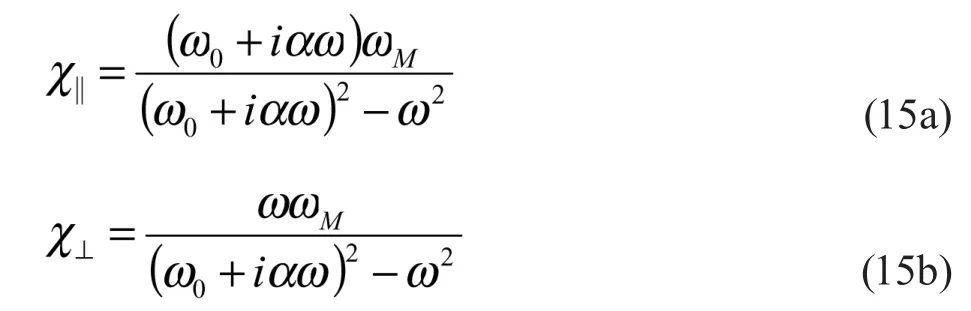
将(15)式与式与(10)式比较。可以得到含有吉伯阻尼项的磁化率与无阻尼的磁化率的区别为无阻尼磁化率中的被替换为。
3 结论
笔者解出了吉伯阻尼磁化率张量与无阻尼磁化率张量满足的关系式(8)。将铁磁体的无阻尼磁化率张量表达式带入(8)式中,得出了铁磁体的吉伯阻尼磁化率张量的形式。这种计算方法对于一阶近似的含有吉伯阻尼项的朗道-栗夫席兹是严格成立的。因此,各种旋磁材料都应该满足(8)给出的磁化率关系。这种方法也可以应用于二阶近似的含有吉伯阻尼项的朗道-栗夫席兹方程的求解,从而得出非线性的有阻尼磁化率张量与无阻尼磁化率张量之间的关系。
[1]廖绍彬.铁磁学(下册)[M].北京:科学出版社,1988.
[2]李卫,姜寿亭.凝聚态磁性物理[M].北京:科学出版社,2006.
[3] 宋启祥.多铁性复合体系室温附近磁电耦合系数增强研究[J].宿州学院学报,2013,(03):94-95.
[4] 蒋磊.磁电耦合对于铁电磁系统的磁性关联的影响[J].苏州大学学报(自然科学版),2007,(01):133-134.
[5] 曾远文.磁性半导体[J].自然杂志,1980,(06):73-74.
Vector solution of Gilbert damping magnetic susceptibility tensor
ZHU Rui-hua,YU Miao
(School of Physics and Electronic Engineering,Mudanjiang Normal University,Mudanjiang 175012,China)
The Landua-Lifshitz equation containing Gilbert damping term are solved by vector operations with the first order approximation.The relation between no damping magnetic susceptibilities tensor and the Gilbert damping susceptibility tensor is
in this paper.This formulation is valid for different magnetic materials.Using this formulation,the ferromagnet's Gilbert damping magnetic susceptibility tensor are achieved from the no damping magnetic susceptibility tensor.
Landua-Lifshitzequation;Gilbert damping;Magnetic susceptibilitytensors
O482.5
A
1674-8646(2016)16-0026-02
2016-07-03
黑龙江省教育厅科技面上项目资助(12541839);牡丹江师范学院青年学术骨干(G201307)资助
朱瑞华(1980-),男,黑龙江牡丹江人,牡丹江师范学院讲师,硕士,主要从事磁性材料的磁光效应研究。
