基于时间尺度分离的斗门开汛日期预测模型
2016-09-18陈诗琳
陈诗琳
(珠海市斗门区气象局,广东珠海 519100)
基于时间尺度分离的斗门开汛日期预测模型
陈诗琳
(珠海市斗门区气象局,广东珠海519100)
采用小波分析、低通滤波、相关分析、逐步回归以及最优子集回归等方法建立斗门开汛日期的预测模型。将开汛日期序列分解为年际变化和年代际变化2个分量,分别研究其与前期冬季500 hPa高度场、850 hPa风场、海平面气压场和海温场的相关性,并将显著相关区域作为初选因子。通过逐步回归将因子数限制在10个以内,最后应用最优子集回归建立预测模型。结果表明:这种分离时间尺度的回归预测模型具有较好的拟合效果,计算得出的回归序列与原距平序列相关系数为0.81,两者同号率为77.8%,其中相差±7 d以内年份约占42.2%;相差±15 d以内的年份约占75.6%。最后对2012—2014年开汛日期进行试报,其中2012和2014年试报效果较好,误差分别为-5.89和-10.45 d。
预报方法;开汛日期;分离时间尺度;预测模型;斗门
陈诗琳.基于时间尺度分离的斗门开汛日期预测模型[J].广东气象,2016,38(4):26-29.
阳江-斗门一带是广东3个多雨中心之一,年雨量超2 000 mm。斗门位于此多雨中心的东部,地处珠江口西侧,濒临南海,雨水充沛,而前汛期(4—6月)则是其主要降水时段,雨量占全年的42.0%。进入前汛期,标志着进入一个强降水频发、洪涝灾害多发的时期。因此,在每年的前汛期形势预报中,关于开汛日期的预测是气象部门的一项重要工作内容,对政府合理安排农工业生产和防洪防涝工作具有极其重要的意义。一般而言,广东大部分地区的前汛期大致在4—6月,但实际开汛的时间存在地域差异,其中南部较北部稍晚。近年来从不同角度找寻广东前汛期降水影响因子及对开汛日期建立预报模型已有一些工作[1-7],但针对斗门开汛日期的研究几乎没有。本研究将基于前人对广东前汛期降水的研究成果,系统分析不同时间尺度上斗门开汛日期与500 hPa高度场、850 hPa风场、地面气压场和海温场的关系,建立不同时间尺度上斗门开汛日期的预测模型,以期加强对这方面的气候预测。
1 资料和方法
采用NCEP/NCAR的1966—2014年冬季(12月—翌年2月)500 hPa高度场、850 hPa风场、海平面气压场再分析资料,分辨率为2.5°× 2.5°;NOAA的重建海温资料ERSST,分辨率为2°×2°;斗门1967—2014年开汛日期资料,按照中国气象局《华南汛期监测业务规定》,定义单站开汛日为每年自3月1日起,该站录得日雨量≥38 mm的日期。由于2007年起斗门区气象局启用斗门区白蕉镇的新站代替原位于井岸镇的旧站,故对2007—2014年新旧站开汛日期进行对比,结果两者完全一致,故可替用。以上述标准得到历年斗门开汛日期并统计每年开汛日距离3月1日的天数,得到相应的时间序列。
本研究使用小波分析、低通滤波、相关分析、逐步回归以及最优子集回归等方法。
2 分解开汛日期的年际和年代变化分量
对斗门开汛日期的距平序列去除线性趋势后,用Molet小波对其周期进行分析(图1),结果表明,开汛日期存在10年以下的年际变化周期以及15~20年年代际变化周期。以10年为分界点,用低通滤波器滤得开汛日期距平序列中10年及10年以上的年代际变化分量,并用原距平序列减去年代际变化序列得到年代际变化序列(图2),原距平序列标准差为23.8,分解后的序列标准差分别为18.3和10.8,这也体现了分解不同尺度的变化分量的科学合理性。

图1 斗门开汛日期距平序列的小波分析

图2 斗门开汛日期距平序列及其年际、年代际变化分量
3 预报因子的相关筛选
用相关分析法分别研究开汛日期的年际变化、年代际变化与前期冬季(12月—翌年2月)500 hPa高度场、850 hPa风场、地面气压场以及海温场的关系,给定显著性水平为0.05,找寻各气象要素场相应的显著相关区域,并将其区域平均后的气象要素距平序列作为初选预报因子。用上述方法初选出开汛日期的年际变化预报因子21个,年代际变化预报因子23个。
4 建立预测模型及试报
将上述初选因子首先分别对1967—2011年开汛日期的年际变化序列及年代际变化序列进行逐步回归,将因子数限定在10个以内,再利用最优子集回归,根据双评分准则CSC确定最优回归方程,并对2012—2014年开汛日期进行试报。
(1)年际变化的回归方程为:

其中X1、X2、X3和X4皆为850 hPa经向风场因子,对应区域分别为(246°E—273°E,65°S—53°S)、(200°E—220°E,18°S—3°S)、(185°E—215°E,20°N—47°N)和(275°E—300°E,50°N—65°N);X5为海平面气压场因子,对应区域为(120°E—210°E,70°N—90°N)。该回归方程导出的回归序列的方差为15.0,与开汛日期年际变化序列的相关系数达0.83,通过了0.01的显著性水平检验。图3a是年际变化序列与回归序列曲线图,从中可见拟合值与实际值的升降趋势基本一致,对多数波峰和波谷年的预测也与实际基本吻合。
(2)年代际变化的回归方程为:

其中X1、X2为500 hPa高度场因子,对应区域分别为(215°E—236°E,15°N—25°N)、(351°E—360°E,30°N—40°N);X3、X4为海平面气压场因子,对应区域分别为(15°E—60°E,5°S—25°N)、(45°E—58°E,40°N—50°N)、(270°E—282°E,50°S—38°S);X5、X6为海温场因子,对应区域分别为(210°E—230°E,12°N—25°N)。该回归方程导出的回归序列的方差为8.0,与开汛日期年际变化序列的相关系数达0.73,通过0.01的显著性水平检验。图3b是年代际变化序列与回归序列曲线图,从中可见拟合值与实际值的升降趋势基本一致。
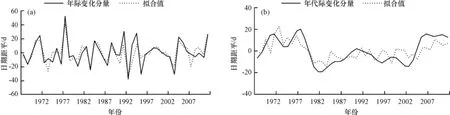
图3 回归方程对1967—2011年斗门开汛日期的年际尺度(a);年代际尺度(b)的拟合值和实况值对比
将年际变化和年代际变化分量的回归方程相加得到斗门开汛日期距平序列的回归方程,即Y=Y1+Y2,开汛日期的回归序列与原距平序列相关系数为0.81,通过0.01的显著性水平检验。由图4可见该回归方程对开汛日期偏早或偏晚的趋势拟合得还是比较好的,进一步分析得到,回归序列与原距平序列同号率为77.8%,其中相差±7 d以内的有19年,约占42.2%;相差± 15 d以内的有34年,约占75.6%;亦有相差超过±20 d的年份,约占13.3%。

图4 回归方程对1967—2011年斗门开讯日期的拟合值与实况值对比
试报2012—2014的开汛日期,结果见表1。用Y1试报开汛日期距平值的年际变化分量,结果表明,该方程对2012和2014年试报效果较好,试报结果和实际值相差皆在±6 d以内,而对2013年的预报效果相对没那么好,相差近20 d;用Y2试报开汛日期距平值的年代际变化分量,该方程对2012和2013年试报效果较好,试报结果和实际值相差皆在±1 d以内,而对2014年的试报结果也与实际值相差小于10 d。2个分量的试报结果相加分别得到3年的开汛日期距平值的试报结果,与实际值相比,2012和2014年试报效果不错,误差分别为-5.89和-10.45 d。
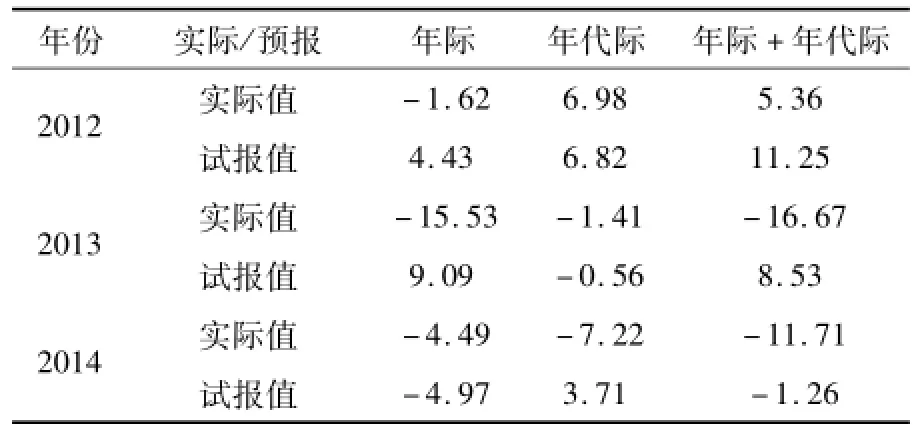
表1 2012—2014年斗门开汛日期距平值试报结果d
5 结论
1)斗门开汛日期存在10年以下的年际变化周期以及15~20年左右的年代际变化周期。
2)斗门开汛日期的年际变化和年代际变化受外部因素的影响,在前期冬季(12月—翌年2月)500 hPa高度场、850 hPa风场、地面气压场以及海温场上分别存在21个和23个显著相关区域,以其区域平均后的气象要素距平序列作为年际变化和年代际变化的回归方程的初选预报因子。
3)用分尺度最优子集回归方法建立斗门开汛日期回归方程,计算得出的回归序列与原距平序列相关系数为0.81,通过0.01的显著性水平检验,两者同号率为77.8%,其中相差±7 d以内的有19年,约占42.2%;相差±15 d以内的有34年,约占75.6%;亦有相差超过±20 d的年份,约占13.3%。总体而言,分尺度回归预测模型具有较好的拟合效果。
4)利用回归方程试报2012—2014年的开汛日期,年际变化方面除2013年外,其余2年的试报效果不错,误差皆在6 d以内;年代际变化方面,3年的试报值都与实际值相差不大,试报效果非常好;将两者相加得到开汛日期的试报结果,其中2012和2014年试报效果不错,误差分别为-5.89和-10.45 d。
分尺度建立预测模型相较于直接对原序列建立预测模型而言,不会过于注重序列的年际变化特征而忽略了其年代际变化特征,考虑了影响其年代际变化的相关物理因素,这对于建立预测模型有很好的指示意义。然而气象预测是一个复杂的问题,影响因素也数之不尽,本研究建立的预测模型仅考虑了4个方面的因素,其他因素还有待研究和补充。
[1]林爱兰.广东前汛期月降水异常的强信号研究及预测概念模型[J].热带气象学报,2002,18(3):219-226.
[2]林爱兰.广东前汛期降水预报因子的初步探讨[J].广东气象,1998,20(SⅠ):58-61.
[3]黄先香,炎利军,施能.华南前汛期旱涝影响因子和预报方法[J].热带气象学报,2006,22(5):431-438.
[4]伍红雨,杨崧,蒋兴文.华南前汛期开始日期异常与大气环流和海温变化的关系[J].气象学报,2015,73(2):319-330.
[5]谷德军,高晓荣,纪忠萍,等.广东开汛日期的多尺度物理统计预测模型[J].高原气象,2012,31(3):768 -776.
[6]黄颖,金龙.华南前汛期降水预测模型及其预测试验[J].热带气象学报,2011,27(5):753-757.
[7]邓立平,王谦谦.华南前汛期(4-6月)降水异常特征及其与我国近海海温的关系[J].热带气象学报,2002,18(1):45-55.
[8]彭京备,陈烈庭,张庆云.多因子和多尺度合成中国夏季降水预测模型及预报试验[J].大气科学,2006,30(4):596-608.
[9]魏凤英,黄嘉佑.大气环流降尺度因子在中国东部夏季降水预测中的作用[J].大气科学,2010,34(1):202-212.
[10]陈慧娴,黄露菁.陈创买.用逐步回归方法预报番禺年降水量[J].广东气象,2004,26(4):7-9.
[11]彭端,黄天文,郭媚媚,等.用逐步回归模型预测肇庆市汛期降水[J].广东气象,2005,27(2):16-20.
[12]农吉夫,金龙.月平均降水量的二次规划最优组合预测方法研究[J].热带气象学报,2004,20(6):704 -709.
[13]覃志年,胡娅敏,陈丽娟.广西夏季降水的多时间尺度特征及影响因子[J].应用气象学报,2013,24(5):565-575.
[14]顾伟宗,陈丽娟,李维京,等.降尺度方法在中国不同区域夏季降水预测中的应用[J].气象学报,2012,70(2):202-212.
[15]魏凤英.我国短期气候预测的物理基础及其预测思路[J].应用气象学报,2000,11(增刊):11-20.
[16]陈桂英.我国现有短期气候业务预测方法综述[J].应用气象学报,2005(2):16-20.
[17]高亭亭,梁卫.广州前汛期暴雨气候特征分析[J].广东气象,2012,34(2):1-9.
[18]邹仁爱,陈俊鸿.雷州半岛年降水量序列分析及预测模型[J].水文,2006,26(1):55-59.
[19]李永华,刘德,金龙.基于BP神经网络的汛期降水预测模型研究[J].气象科学,2002,22(4):461-467.
A Prediction Model for Rain Season Onset Dates in Doumen District Based on A Multiscale Decomposition
CHEN Shi-lin
(Zhuhai Doumen Meteorological Service,Zhuhai 519100)
Using the wavelet analysis,lowpass filtering,stepwise regression and optimal subset regression,we constructed a prediction model for rain season onset dates in Doumen.The time series of onset dates was decomposed into interdecadal and interannual scales,and their relationship with the 500 hPa height,850 hPa wind,sea level pressure and sea surface temperature in precedent winters was analyzed respectively to select primary predictors.Then stepwise regression is applied to limit the number of predictors to be within ten and finally a prediction model was constructed by using optimal subset regression.The results show that the prediction model has a good regression effect.The correlation coefficient between the regression and observation is 0.81,the percentage of hits of the same-sign symbol is 77.8%,the difference of less than 7 days is 42.2%and that of less than 15 days is 75.6%.The forecast results of 2012 and 2014 are good,and the prediction errors are-5.89 and-10.45 days respectively.
forecast;rain season onset dates;decomposition of time scales;prediction model;Doumen District
P456
A
10.3969/j.issn.1007-6190.2016.04.006
2015-12-01
陈诗琳(1990年生),女,硕士,主要从事短期及短时天气分析与预报工作。E-mail:15819478226@139.com
