基于ELM的大坝变形分析与预报模型
2016-09-16邵楠于中伟
邵楠,于中伟
(沈阳市勘察测绘研究院,辽宁沈阳 110004)
基于ELM的大坝变形分析与预报模型
邵楠*,于中伟
(沈阳市勘察测绘研究院,辽宁沈阳 110004)
传统的诸如BP神经网络等学习方法训练时需要设置大量的参数,并且容易产生局部最优解。极限学习机(Extreme Learning Machine,ELM)可以随机选择输入权重以及隐藏层偏差且不需要调节,最终只产生唯一最优解。将ELM引入大坝变形分析建模中,建立了基于ELM的变形预报模型。实例表明,相比传统的逐步回归模型与BP神经网络模型,基于ELM的大坝变形预报模型在效率和精度上都有提高。
大坝变形预报;物理模型;神经网络模型;极限学习机(ELM)
1 引 言
对大坝变形监测数据进行整理分析,是保证大坝安全运营的重要手段[1,2]。大坝安全监测数学模型主要分为几何模型和物理模型。其中,物理模型以回归模型为主,利用多元线性回归或相应改进方法建立大坝变形与温度、水位和时效因子之间的关系[3,4]。但回归模型只能反映监测效应量与自变量之间的线性关系,模型精度会因此受到一定影响。随后,有学者建立了基于神经网络算法的变形预报模型,建立了位移与环境自变量之间的非线性模型,验证了神经网络算法在大坝变形预报中的应用的有效性[5,6]。
极限学习机(Extreme Learning Machine,ELM)是新加坡Huang等人[7,8]在2004年提出的一种单隐层前馈神经网络的方法。相比传统的诸如BP神经网络,ELM优点是在极快的学习速度上有着良好的泛化能力。基于以上优点,极限学习机已经在生物医学[9]、机器视觉[10]、图像视频处理[11]等方面得到了广泛的应用。本文将ELM应用在大坝变形预报中,结合影响大坝变形的环境因子建立基于ELM的大坝变形监测模型,并与传统的逐步回归模型和BP神经网络模型进行对比分析,验证ELM算法的优势。
2 极限学习机基本原理
对于给定的N个样本(xi,ti),其中xi=[xi1,xi2,…,xin]T∈Rn,ti=[ti1,ti2,…,tin]T∈Rm,含有个隐藏节点的单隐层前馈神经网络的激活函数为:
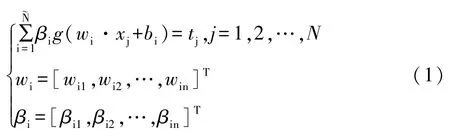
其中,wi是输入层与第i层隐藏层的权重,βi是第i层隐藏层与输出层的权重,bi是第i层隐藏层节点的阈值,g(x)为激活函数。
若把激活函数看成一个用H简写的矩阵,那么式(1)可简化为:

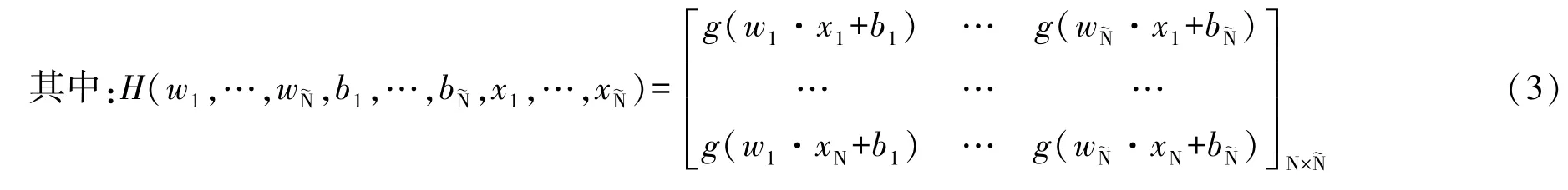
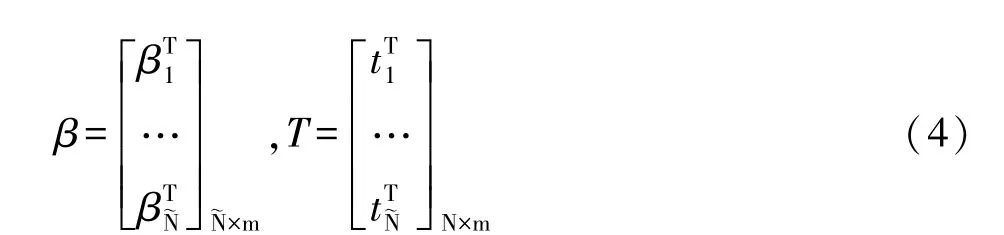
式中,H所代表的矩阵就是神经网络隐藏层的输出矩阵。

在极限学习机中,激活函数无限可微的情况下,单隐层前馈神经网络的输入权重和隐藏层偏差都不需要调整。那么训练这个单隐层前馈神经网络就等价于求式(1)中线性系统的最小二乘解:

根据广义逆矩阵的定义,这个线性系统Hβ=T的最小二乘解的最小范数为:

在变形监测领域,基于神经网络的变形建模属于物理模型,即将影响变形体变形的物理环境量作为输入变量,变形值作为输出变量,利用上述原理进行训练求解,建立应变量与效应量之间的关系。在基于极限学习机的大坝变形模型中,选取合适的变形效应量进行建模分析是十分必要的。
3 基于ELM的大坝变形预报模型
3.1ELM模型输入变量选择
大坝安全监测模型是根据已取得的监测资料,以环境作为自变量,以监测的大坝变形位移作为效应量建立的变形与环境量之间的关系的模型。已有的坝工知识表明,大坝上任一点在某时刻的变形主要受大坝上下游水位差(水压)、温度以及时效等因素的影响[1]。因此,本文针对某混凝土大坝上某测点的引张线一年内的大坝水平位移监测数据进行建模分析,时间分辨率为1 d,共365期观测数据。同时收集了一年内大坝上下游水位差数据和当地温度数据参与建模。水位和温度数据观测频率均为1 d。
根据相关力学公式推导,水压作用引起的混凝土坝上某一点的水平位移与水压H的1~3次方有关,实际统计建模应用中,一般统一取到4次项,因此,水位因子选取为:H、H2、H3、H4,H为上下游水位差。
温度分量一般取决于大坝坝体温度场变化,但由于坝体温度资料有限,我们指收集到相关气温数据。考虑到坝体温度主要受外界气温变化影响,因此可以用气温间接描述坝体温度场变化。由于坝体内部温度相对于气温变化存在滞后效应,因此一般采用监测变形量观测日前若干天气温的平均气温作为温度因子。在本文建模中,温度因子选取为:T0-1、T2-7、T8-30、T31-60,分别为前0 d~1 d、2 d~7 d、8 d~30 d、31 d~60 d的平均气温;
大坝建模中的时效分量是指随着时间推移,坝体向某一方向发展的不可逆的变形分量。一般情况下,大坝从建成到稳定状况,时效位移会趋于稳定。因此,本次建模中,时效因子选取为为:θ、lnθ,θ为观测日天数减去基准日天数再除以100。
3.2建模结果及分析
在利用ELM建模中,选取以上10个因子作为建模中的输入变量。为了消除数值的影响,所有建模中的因子数据均进行了标准化处理。分别利用ELM和BP神经网络模型对大坝一年内的变量因子和变形数据进行训练建模,得到大坝的变形分析模型。同时采用目前大坝变形建模中最常用的逐步回归方法进行建模对比分析。三种模型的拟合效果如图1所示。图中可以看出,三种模型都准确反映了大坝的真实变形状况,有着较好的拟合效果。相比逐步回归,ELM和BP模型建立了自变量与大坝位移间的非线性关系,模型更加准确。
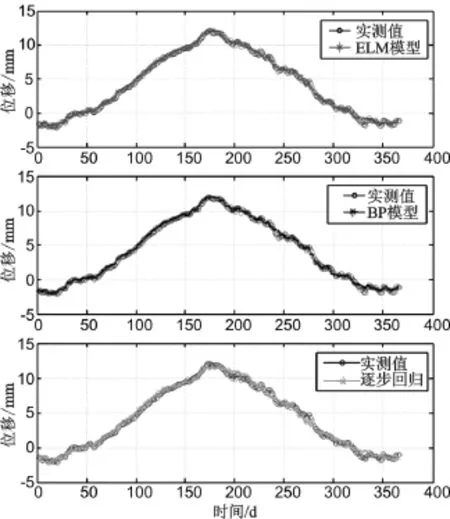
图1 三种大坝变形模型的拟合效果
在采用传统的逐步回归模型建立大坝变形模型中,回归模型中的自变量选择与ELM模型的输入变量相同,建模结果结果如表1所示。逐步回归中,剔除了前两项不显著的自变量因子,模型复相关系数R=0.9960,回归方程显著性检验统计量F=5564.3926。所建立的回归模型是可靠合理的。
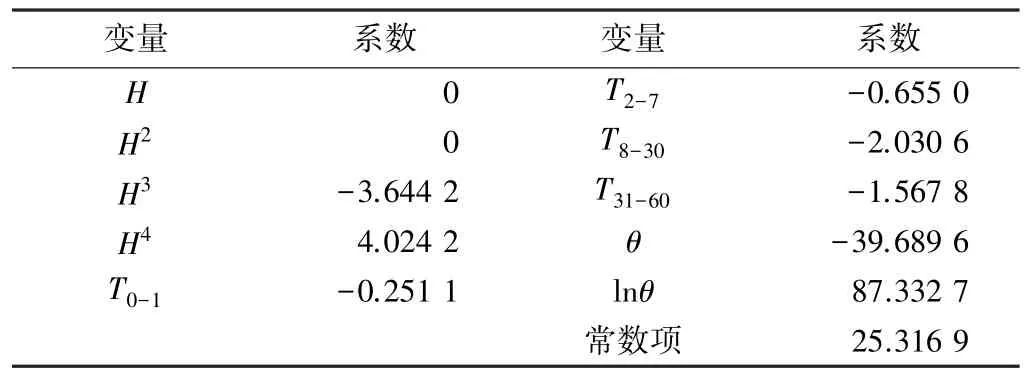
逐步回归模型系数 表1
接着,利用建立的逐步回归模型与训练好的ELM模型和BP神经网络模型结合变量因子对接下来30 d的大坝变形状况进行预测,同时结合引张线实测数据进行对比分析,来验证各模型对大坝变形的预测能力。三种模型的拟合与预测统计结果如表2所示,统计中,将引张线实测数据作为大坝变形的真值。三种模型的预测结果如图2所示。

逐步回归模型、ELM和BP神经网络模型中残差RMS值 表2
表2的结果表明逐步回归模型在大坝建模中效果最不理想。这是由于虽然自变量中加入了环境因子的非线性项,但回归方法仍然是针对自变量的线性统计建模,不能准确反映大坝变形与自变量因子之间的复杂关系。ELM和BP神经网络模型则属于非线性统计模型,在大坝变形建模与预测精度上都有很大改善。其中,ELM的预测效果如图2所示。
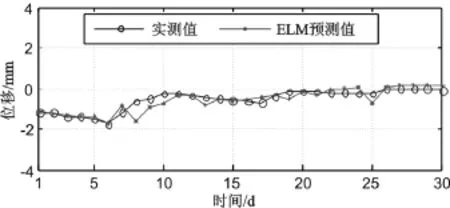
图2 大坝ELM模型预测效果
两种神经网络模型都能较好地拟合大坝实际变形位移序列,但相比BP神经网络模型,基于ELM的大坝变形分析模型有着更高的预测精度。同时,在实验过程中,ELM模型相比BP神经网络模型在运算效率上有着明显优势。
4 结 论
建立大坝位移监测模型,是分析大坝变形状况,保障大坝安全运营的重要手段。本文研究了利用ELM建立大坝变形分析模型的方法。结合影响大坝变形的变量因子选取了ELM建模中的输入变量,建立了基于ELM的大坝位移监测模型;模型能准确反映大坝变形状况,有着较高的预测精度;同时,相比BP神经网络模型,ELM模型只产生唯一解,模型更具稳定性,且相比BP神经网络模型,ELM算法在计算效率上有着明显的优势。
[1]何金平.大坝安全监测理论与应用[M].北京:中国水利水电出版社,2010.
[2]修延霞,侯凯.卡尔曼滤波在大坝变形监测中的应用[J].城市勘测,2010(1):92~94.
[3]李红祥,岳东杰,李立瑞.基于主成分回归的大坝位移模型[J].水电自动化与大坝监测,2008,32(5):61~64.
[4]Dai Wujiao,Liu Bin,Ding Xiaoli,et al.Modeling dam deformation using independent component regression method[J].Trans. Nonferrous Met.Soc.China,2013,23(7):2194~2200.
[5]徐晖,李钢.基于Matlab的BP神经网络在大坝观测数据处理中的应用[J].武汉大学学报:工学版,2005,38(3):50~53.
[6]吴云芳,李珍照,徐帆.BP神经网络在大坝安全综合评价中的应用[J].河海大学学报·自然科学版,2003,31 (1):25~29.
[7]Huang G.B.,Zhu Q.Y.,Siew C.K.Extreme learning machine:a new learning scheme of feedforward neural networks [C]//Neural Networks,2004.Proceedings.2004 IEEE International Joint Conference onvol.2:985~990.
[8]Huang G.B.,Zhu Q.Y.,Siew C.K.Extreme learning machine:Theory and applications[J].Neurocomputing,2006,70(1-3):489~501.
[9]陈津津,赵于前,邹润民.基于超限学习机的腹部CT序列图像肝脏自动分割[J].中国医学物理学杂志,2015,32 (5):611~616.
[10]He Bo,Xu Dongxun,Nian Rui,et al.Fast Face Recognition Via Sparse Coding and Extreme Learning Machine[J].Cognitive Computation,2013.
[11]Bazi Y.,Alajlan N.,Melgani F.,et al.Differential Evolution Extreme Learning Machine for the Classification of Hyperspectral Images[J].IEEEGeosci Remote SensLett,2014,11 (6):1066~1070.
Dam Deformation Analysis and Prediction Model Based on Extreme Learning Machine
Shao Nan,Yu Zhongwei
(Shenyang Geotechnical Investigation&Surveying Research Institute,Shenyang 110004,China)
Traditional learning methods such like Back Propagation(BP)neural network training need to set a number of parameters,and prone to local optimal solution.Extreme Learning Machine(ELM)randomly chooses the input weighs and the hidden layer biases and does not necessarily tuned.Finally it generates a unique optimal solution.In this paper,ELM algorithm is introduced in dam deformation analysis modelling,establishing a dam deformation and prediction model.Experimental results show that compared with BP neural networks model,the dam deformation prediction model based on ELM have improved on efficiency and accuracy.
dam deformation prediction;physical model;neural networks model;extreme learning machine
1672-8262(2016)04-134-03
P258
B
2016—04—05
邵楠(1989—),男,硕士,工程师,主要从事工程测量方面的工作。
