三角恒等变换和解三角形,想说爱你不容易
——有感于高一习题课中一个习题的数学
2016-09-16李雪娇浙江省临海市杜桥中学
李雪娇(浙江省临海市杜桥中学)
三角恒等变换和解三角形,想说爱你不容易
——有感于高一习题课中一个习题的数学
李雪娇
(浙江省临海市杜桥中学)
三角恒等变换和解三角形是高中数学的重要内容之一,因此三角恒等变换与解三角形是三角函数部分的重要内容,也是这几年浙江省数学高考必考的一个重要知识点。
三角恒等变换;解三角形;正弦定理;余弦定理;数学思想
在高考的大背景下,三角恒等变换及解三角形的教学是个重要内容。考查时以中、低档题为主,是高考得分的关键点,笔者对所在的学校高三学生解答三角题目的得分做了长期的统计,发现得分率并不高,容易出现这样那样的错误,解答题得满分的学生较少,我常把这种现象叫做“三角,想说爱你不容易!”针对高三出现的这种现象,笔者分析高一的学习是关键,要从高一开始做起,打好基础。下面是笔者在高一必修5一节复习课时对例题的设计和讲解,以此来复习和强化三角恒等变换及解三角形的知识。
例题:在△ABC中,角A,B,C的对应边为a,b,c且c cos B+ b cos C=2a cos B
分析:将已知条件进行转化,找到比较明显的边的关系或角的关系.这类问题通常需要运用正弦定理或余弦定理,并结合三角恒等变换公式将条件中的边角关系统一到边的关系或角的关系,即“角化边”或“边化角”.“角化边”或“边化角”是解决这类问题常见的思维出发点.
(1)对于式子c cos B+b cos C=2a cos B,可以有以下几种解法,
可对其利用正弦定理得到sin C cos B+sin B cos C=2sin A cos B即
或者也可利用余弦定理得到

其实c cos B+bcos C是向量投影概念的应用,即c cos B+bcos C=a,
所以由c cos B+bcos C=2a cos B马上得到所以B=60°
(2)由(1)知B=60°,先用余弦定理b2=a2+c2-2a cos B求得ac,再可以用面积公式计算出结果。
我们的学生在(2)小题中存在的困惑是选择公式时不够准确,纠结在余弦定理和面积公式三个式子里选择哪个,笔者在教学中教给他们一个不是规定的约定,就是已知哪个角就用含有这个角正弦值的面积公式,用含有这个角余弦值的余弦公式。学生掌握得也较快。下面是对(2)小题进行变式:

变6:若在开始的条件中,改变成在锐角△ABC中,那么从“变1~变5”中哪些结果会变。
分析:来看变2和变3,此题可以先写出余弦定理b2=a2+c2-2ac cos B,再用基本不等式可得,又因为三角形两边之和大于第三边得到

来看变4,此题可以先写出余弦定理b2=a2+c2-2a cos B,再用基本不等式得到3=a2+c2-ac≥ac当a=c时(ac)max=3,进而能求出面积的最大值。
但是当有了“锐角三角形”这个条件的限制时,用基本不等式还要会再加其他的条件来进行求范围,显得有点麻烦,对于高一的学生有些难以接受。所以笔者就针对高一学生的知识储备和知识结构,对上述的几个变式采用了边到角的转化,实现了两条边(即两个未知量)到一个角(即一个未知量)的转化。
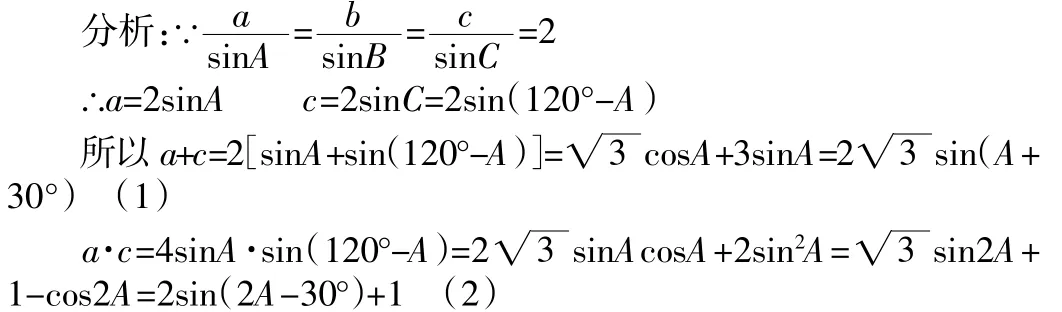
若是任意三角形,则A的范围容易确定0°<A<120°,则利用三角函数知识能求得(1)式和(2)式的范围。
若三角形是锐角三角形,则确定A的范围是关键,也是一个难点。因为是锐角三角形,所以三角形的三个内角都必须是锐角,可做这样的限制。
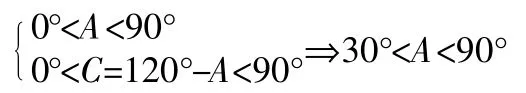
再利用三角函数知识能求得(1)式和(2)式的范围。
评注:
1.易错点拨。在解题过程中,由于三角恒等变换和解三角形中公式众多需灵活运用,且常需要对角的范围及三角函数值的符号等进行讨论,甚至需要对题设中的隐含条件进行挖掘,故解题时稍有不慎,就会出现漏解、增解等现象。合理运用三角公式是解决三角函数的图象与性质、三角求值及解三角形这几类问题的关键。高一的学生还要不断地进行训练。
2.利用数学思想方法进行变换。数学思想与方法是数学知识在更高层次上的概括,利用它来指导我们解题,会让我们思维顿开。它蕴涵在数学知识发生、发展和应用的过程中,本题用到的思想方法主要有转化与化归思想、整体化思想、特殊与一般化思想。
下面是我为上述这个例题准备的反馈练习:
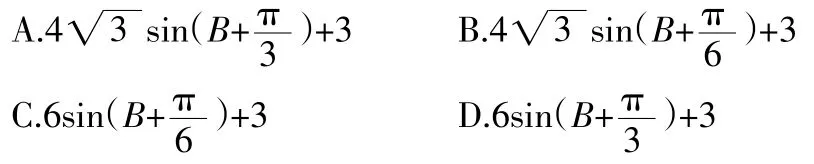
在选出的选项中求周长的最大值________;
……
通过本题的教学,学生收获比较大,本题目比较综合,将三角恒等变换和解三角形综合在一起,题中用到了恒等变换中的变角、降幂、辅助角公式、正弦定理、余弦定理,并能运用正、余弦这两个定理解决周长和面积问题。通过变式讲解,反馈题目做得较好,效果不错。
在高中数学解题中,变换是其主要工具之一,通过变换能够将复杂公式简单化,简单明了,通过变换能将复杂问题简单化,利于学生理解。总之,解答三角恒等变换的题目的方法多样,万变不离其宗,要注意灵活运用,最后借用名师教给我们的口诀,要努力做到“三看”,即
(1)看角,把角尽量向特殊角或可计算角转化;
(2)看名,把一道等式尽量化成同一名称或相近的名称,例如把所有的切都转化为相应的弦,或把所有的弦转化为相应的切;
(3)看式,看式子是否满足三角函数的公式。如果满足直接使用,如果不满足转化一下角或转换一下名称,就可以使用。
·编辑谢尾合
