基于频谱扩展的合成孔径雷达盲移频干扰方法
2016-09-16房明星毕大平沈爱国
房明星,毕大平,沈爱国
(解放军电子工程学院,安徽 合肥 230037)
基于频谱扩展的合成孔径雷达盲移频干扰方法
房明星,毕大平,沈爱国
(解放军电子工程学院,安徽 合肥230037)
针对传统的SAR移频干扰无法对波形捷变信号实施有效干扰的缺点,提出基于频谱扩展的SAR盲移频干扰方法。该方法利用线性调频信号的时延-移频耦合特性,首先将两路信号进行频谱扩展,然后对两路扩展信号进行频谱压缩产生干扰信号,从而将频谱扩展后的信号恢复成原来的SAR回波信号样式,并引入移频干扰相位调制项。理论分析和仿真实验表明:该方法可在SAR距离向产生前移、滞后的假目标干扰,且无需获取信号的调频斜率信息,能够有效对抗波形捷变SAR雷达信号,是一种盲移频干扰方法。
合成孔径雷达;频谱扩展;频谱压缩;盲移频干扰
0 引言
合成孔径雷达(SAR)是一种高分辨率成像雷达,具有全天时、全天候和透视性等特点,已广泛用于军事侦查、地图测绘以及导弹末端图像匹配制导等方面[1]。尤其在高技术局部战争(如阿富汗战争、伊拉克战争等)中发挥的巨大作用,使得SAR干扰技术研究成为电子对抗领域的热点问题[2-5]。随着SAR干扰技术的发展成熟,以波形捷变为代表的SAR抗干扰技术也得到了快速发展。波形捷变SAR发射慢时间域参数捷变的雷达信号(本文主要指调频斜率捷变或调频斜率分集),并通过匹配接收和惩罚函数来抑制传统的压制和欺骗干扰[6-8]。目前,对波形捷变SAR干扰技术研究相对较少,其主要干扰手段是基于数字射频存储器的间歇采样转发干扰,干扰的可行性和有效性仍需进一步验证[9-10]。
当前,对SAR的传统移频干扰技术已比较成熟,但针对波形捷变SAR的移频干扰技术却少有研究。文献[11]通过脉冲压缩信号的时延-移频耦合特性,提出了SAR移频干扰方法,该方法可在SAR距离向形成逼真的假目标欺骗干扰;文献[12—14]则针对固定移频干扰只能形成点目标干扰的局限,分别提出了SAR随机移频干扰和步径移频干扰方法,两种干扰方法的输出为干扰条带或干扰区域,具有一定压制干扰效果,但都是以牺牲干扰功率为代价的。上述方法虽然对SAR可以产生假目标欺骗或压制干扰效果,但要精确控制假目标的位置,都需要事先知道雷达信号的调频斜率等参数信息,当SAR信号波形捷变时,假目标在多个不同距离进行跳变或无法获得相干处理增益,从而容易被识别滤除,导致干扰效果严重降低[14]。本文针对此问题,提出了基于频谱扩展的SAR盲移频干扰方法。
1 传统的SAR移频干扰原理
设SAR发射的线性调频信号表达式为:
(1)
其中rect(·)为矩形窗函数,tr为距离向快时间,ta=mT(m=0,1,2,…,M)为方位向慢时间,T为脉冲重复周期,全时间t=tr+ta,Tp为脉冲宽度,f0为载频,ur为调频斜率。
则SAR接收到的点目标基频回波信号为:
(2)
其中τr=2R(ta)/c,tr-τr为回波到达接收机的时间,TL为合成孔径时间。
传统的SAR移频干扰是指在距离向进行的固定移频干扰,假设固定移频量为ξ,则传统的SAR移频干扰信号表达式为[11]:
(3)
采用经典R-D成像算法进行距离向和方位向脉压处理,则经过脉压处理后的回波信号和干扰信号包络的表达式为:
(4)
(5)
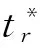
(6)
由式(6)可知,假目标距离偏移量ΔR与移频量ξ成正比,与调频斜率ur成反比,当ξ固定、ur捷变时,ΔR随ur变化而改变,从而造成假目标位置的跳变。同时,根据线性调频信号模糊函数的时延-移频耦合效应,频移干扰信号回波经距离向匹配滤波处理后会引起失配,干扰功率会出现相应失配损失,由式(5)可得干扰信号峰值增益为:
(7)
通过上述分析可知,传统的SAR移频干扰可在距离向形成前移或滞后的假目标干扰,克服了延迟转发干扰无法形成前移假目标干扰的缺点。但传统移频干扰要实现精确的假目标位置控制,必须知道准确的雷达信号调频斜率等参数的先验信息,当SAR雷达信号的波形捷变时,假目标位置在距离向进行跳变,无法进行方位向的脉冲积累,因而无法对波形捷变信号形成有效干扰。
2 基于频谱扩展的SAR盲移频干扰原理
传统的SAR移频干扰容易被识别、滤除,且对波形捷变信号难以产生有效干扰,针对传统的SAR移频干扰缺点,本节提出基于频谱扩展的SAR盲移频干扰方法。
2.1干扰信号的产生
对SAR雷达接收的点目标基频回波信号sr(tr,ta)在二维时域进行N+1次幂运算(N≥0),即
(8)
由式(8)可知,通过对回波信号的N+1次幂运算,SAR距离快时间域线性调频信号调频率变为(N+1)ur,频谱扩展为原来的N+1倍,同时方位慢时间域频谱也扩展为原来的N+1倍。需要指出的是,这里所说的频谱扩展是对下变频后的基频SAR信号而言,扩展后的信号瞬时带宽通常控制在1 GHz范围内,因而不会超出干扰系统的通带宽度。
SAR雷达无法对N+1倍频谱扩展后的信号进行脉压处理,必须将式(8)恢复成原信号形式,并引入移频干扰分量,此时对sr(tr,ta)在快时间域延时τ并进行N次幂频谱扩展可得(忽略快时间域微小延迟τ对慢时间域的影响)
(9)
对两路扩展信号进行频谱压缩产生干扰信号,即将式(8)、(9)进行共轭相乘可得干扰信号为
(10)
令t=tr-τr,式(10)的具体表达式为
exp(-j2πf0τr)=sr(tr,ta)exp(j2ξt+jΔφ),
(11)
其中,ξ=Nurτ为干扰信号移频量,Δφ=-πNurτ2为常数相位项。由式(11)可知,通过对回波信号进行两次频谱扩展和共轭相乘处理,不仅将频谱扩展后的信号恢复成原来的SAR回波信号样式,而且成功地引入了移频干扰相位调制项,干扰信号产生原理框图如图1。

图1 基于频谱扩展的移频干扰信号产生框图Fig.1 The shift-frequency jamming signal block diagram based on spread spectrum
具体的干扰信号产生过程为:首先干扰机将接收到的SAR信号进行下变频和分路处理,并对第一路信号延时τ后进行N倍频谱扩展,对第二路信号直接进行N+1倍频谱扩展,然后将两路扩展信号进行频谱压缩和上变频处理,即可产生所需的干扰信号。此时就将频谱扩展后的信号恢复为原来的SAR雷达信号样式,并完成干扰信号的移频调制。
利用上述原理产生的盲移频量ξ>0,可产生前移的假目标干扰,同理,也可利用本文方法产生负移频干扰信号,从而产生滞后的假目标,其干扰信号产生原理框图如图2。
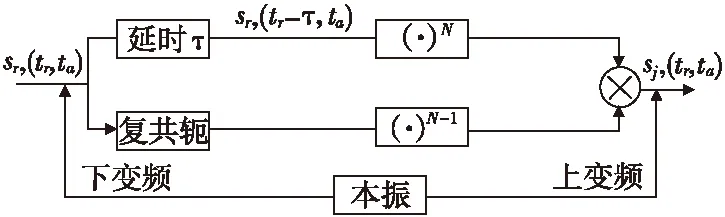
图2 基于频谱扩展的负移频干扰信号产生框图Fig.2 The negative shift-frequency jamming signal block diagram based on spread spectrum
2.2匹配滤波器输出

Srout(tr,ta)=sj(tr,ta)*hr(tr)=
(12)
其中“*”表示“卷积”,将正移频ξ=Nurτ代入上式可得
Srout(tr,ta)=sj(tr,ta)*hr(tr)=
(13)
其中,t*为经过距离徙动校正的距离向快时间,由式(13)可知,本文方法产生的移频干扰信号经过SAR距离向匹配滤波后的表达式分为三个区间:
在第一区间即(-Tp+τ,0]范围内时,输出幅度和主瓣宽度都是关于1+(t*-τ)/Tp的变量,且距离向快时间的附加相位项为Δψ=(N-1)πurτtr-πξτ。特殊情况,当N=0时,由式(10)可知,sj(tr,ta)=sr(tr,ta),为直接转发式干扰(不考虑系统的转发延迟);当N=1,Δψ=-πξτ为常数相位项,此时干扰信号不存在传统移频干扰的固定移频量ξ/2,具有很强的抗干扰识别性能。
在第二区间即(0,τ]范围内时,输出幅度和主瓣宽度都为常数(1-τ/Tp),距离向快时间附加相位项为线性调频信号,Δψ=(2N-1)πurτtr+πurtr2-πξτ。
在第三区间即(τ,Tp]范围内时,输出信号表达式与传统移频干扰信号相同,距离向快时间附加相位项Δψ=πξtr,产生固定移频量ξ/2。

Sjout(tr,ta)=Srout(tr,ta)*ha(ta)=
(14)
当t*=-Nτ时,可得干扰信号峰值增益为:
(15)
距离向主瓣宽度展宽为原来的Tp/(Tp-Nτ-τ)倍,正移频干扰对SAR所产生的前移假目标距离向偏移量为
(16)
对比式(6)、式(16)可知,本文干扰方法产生的假目标距离偏移量ΔR只取决于N和延时τ,不需要知道信号的调频斜率,因而能够有效对抗调频率捷变和调频率分集等信号样式,属于盲移频干扰方式。
2.3干扰信号关键参数分析
根据式(10)可知,本文SAR雷达干扰信号产生只依赖于阶数N和延时τ,而不需要知道雷达信号调频斜率信息,且干扰信号峰值增益G和距离偏移量ΔR只与阶数N和延时τ有关,则由式(15)、(16)可得τ和G的表达式为:
(17)
(18)
其中假目标距离偏移量ΔR与阶数N是预先设定的,则通过式(17)可计算延时τ,若SAR信号的脉冲宽度Tp也已知,则通过式(18)可得到假目标干扰信号峰值增益G。
实际干扰中,参数τ>0,G>0,分别代入式(17)、式(18)可得假目标距离偏移量的范围为
(19)
其中ΔR≥0表示正移频所产生的是前移假目标,通过式(16)、式(19)可知,ΔR的取值仅与N、τ,Tp有关,与SAR信号的线性调频斜率ur无关,因而本文的SAR移频干扰方法具有盲移频干扰的优点。
通过对式(13)第一区间输出函数的分析可知,当N=0时,为直接转发式干扰;当N=1时,干扰信号不存在传统移频干扰的固定移频量ξ/2。通过式(18)、式(19)可知,G与ΔR都是关于N的单调增函数,当N→∝时得到G与ΔR的极限值
(20)
(21)
式(20)、(21)与传统的移频干扰表达式相同,因此本文算法的峰值增益和最大干扰距离是以传统移频干扰为上限的。但是在实际干扰中,SAR雷达信号的带宽已经比较宽,对其进行高阶频谱扩展难以实现;其次,SAR雷达的距离向成像带通常不能做到很宽,因此要充分考虑N和ΔR取值,避免使假目标干扰信号偏移出成像带或接收机距离波门。
结合以上分析,下面给出本文干扰信号参数的推算步骤:1)干扰机系统参数设置:选取满足干扰需求的频谱扩展阶数N值;2)干扰信号产生:确定适当的距离偏移量ΔR,通过式(17)计算延迟τ,并根据式(10)产生盲移频干扰信号;3)干扰效果评估:利用脉冲时宽Tp和合成孔径时间TL等先验信息,结合式(18)、(19)分别计算峰值增益G和ΔR的最大偏移量上限。
3 仿真实验
为了验证本文SAR盲移频干扰的可行性和有效性,下面进行如下仿真实验,仿真实验参数如表1所示。

表1 仿真实验参数
3.1频谱特性分析
考虑到SAR距离向成像带宽度和假目标最大偏移量上限的限制,选取频谱扩展阶数N=4,分别用本文方法和传统移频干扰方法产生前移150 m和400 m的假目标,由表1可得SAR雷达发射信号的调频斜率ur=1.2×1013Hz/s,并根据式(17)得到本文干扰信号产生所需延时τ=0.25 μs。首先对扩展信号的频谱特性进行分析,假设两路扩展信号功率均与真实信号功率相同,图3为两路扩展信号频谱与真实信号频谱的对比结果(去载频),真实信号频谱带宽为60 MHz,第一路扩展信号频谱带宽约为240 MHz,第二路扩展信号频谱带宽约为300 MHz,第一路信号频谱由于延时τ产生约12 MHz的偏移,根据能量守恒定律,两路扩展信号频谱幅度相对真实信号有不同程度的衰减。
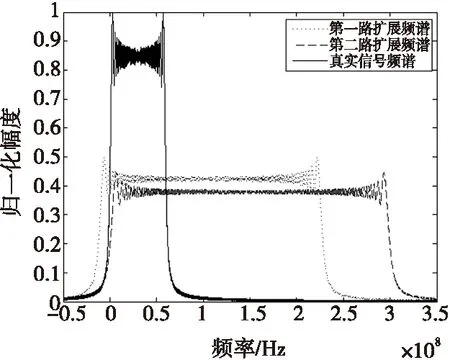
图3 频谱扩展对比Fig.3 Spectrum spread comparison
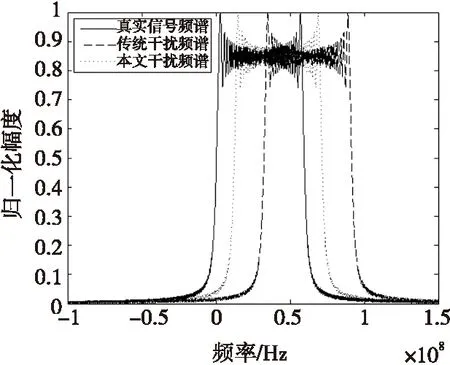
图4 频谱压缩对比Fig.4 Spectrum compression comparison
依据本文方法对两路扩展信号进行频谱压缩,假设压缩后干扰信号功率与真实信号功率相同,图4为压缩后的干扰信号与传统移频干扰信号以及真实信号的频谱对比结果。由图4可以看出,三种信号频谱具有相同的包络和带宽,但两种干扰信号频谱由于移频量不同相对真实信号产生了不同偏移,由式(11)可知,频谱压缩后引入的干扰相位调制项对应的移频量为12 MHz。可见,本文干扰信号的频谱特性与理论分析完全吻合。
3.2与传统移频干扰方法对比
仿真条件不变,在干扰功率和信号回波功率相同情况下,分析本文方法相对传统移频干扰方法对波形捷变信号的适应性。两种移频干扰信号经过SAR系统二维脉压处理后在距离向成像带范围内的回波如图 5(a),从右到左依次为真实信号回波、本文干扰信号回波、传统移频干扰信号回波,图5(b)为对应的SAR二维成像结果。
由图5可知,本文干扰方法和传统移频干扰都能在SAR距离向形成假目标欺骗干扰,但是两种方法在干扰功率上都有一定损失,在实际干扰中需要适当增加干扰机发射功率,从而补偿移频干扰的功率损失。 为了体现本文方法对波形捷变信号具有适应性,改变SAR信号调频斜率为4ur/3和5ur/3,在相同的干扰条件下,干扰输出结果如图6和图7所示。对比分析可知,当SAR信号的调频斜率发生改变时,传统移频干扰产生的假目标相对原来位置分别向真实目标移动了100 m和160 m,而本文干扰方法产生的假目标位置只与阶数N和延时τ有关,不随调频斜率改变而发生偏移,因而对波形捷变信号具有适应性,是一种盲移频干扰方式。

图5 调频斜率为ur时干扰输出Fig.5 The jamming output when frequency modulation slope isur

图6 调频斜率为4ur/3时干扰输出Fig.6 The jamming output when frequency modulation slope is 4ur/3

图7 调频斜率为5ur/3时干扰输出Fig.7 The jamming output when frequency modulation slope is 5ur/3
3.3干扰参数分析
由式(17)可知,干扰信号峰值增益G与阶数N以及偏移量ΔR有关,下面具体分析参数N和ΔR对G的影响。
1)阶数N对峰值增益的影响
为了分析阶数N与干扰信号峰值增益G的关系,固定变量ΔR=300 m,图8所示为干扰信号峰值增益G与阶数N的关系曲线,图中蓝色实线为不同阶数N时G的理想值,红色实心圆点为G的实验仿真值,G的实验值与理想值基本一致。从图8可以看出,在相同条件下,干扰信号峰值增益G随阶数N增大而增大,当N>6时,曲线趋于平缓,G的增量越来越小,所以实际干扰中一般选取N≤6。

图8 阶数N对峰值增益的影响Fig.8 The effect of order Non peak gain
2)偏移量ΔR对峰值增益的影响
同理,为了分析偏移量ΔR与干扰信号峰值增益G的关系,固定变量N=4,图9所示为ΔR间隔50 m连续取值时G随ΔR的变化关系。从图9可以看出,在相同条件下,G随ΔR增大而变小,呈反比关系,与理论值基本一致,实际干扰中ΔR取值要满足式(19)的限制条件。图8和图9仿真结果与理论分析一致,验证了本文方法的可行性与理论推导的正确性。
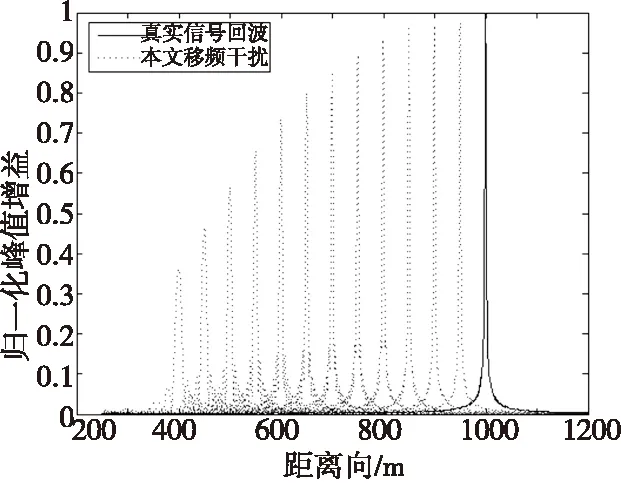
图9 偏移量ΔR对峰值增益的影响Fig.9 The effect of offset ΔR on peak gain
4 结论
本文提出了基于频谱扩展的SAR盲移频干扰方法。该方法利用线性调频信号的时延-移频耦合特性,首先将两路信号进行频谱扩展,然后对两路扩展信号进行频谱压缩产生干扰信号,从而将频谱扩展后的信号恢复成原来的SAR回波信号样式,并引入移频干扰相位调制项。理论分析和仿真实验表明:该方法可在SAR距离向产生前移、滞后的假目标干扰,且无需获取信号的调频斜率信息,能够有效对抗波形捷变SAR雷达信号,是一种盲移频干扰方法。虽然对SAR回波信号进行了频谱扩展,但通过对扩展信号的频谱压缩处理,干扰信号恢复为原来SAR回波信号样式,并未改变输出信号的频谱范围,因此不会增加系统的采样率和带通滤波器的通带宽度。本文方法只能在SAR距离向产生移频干扰效果,如何结合本文方法对SAR形成多维、多样化的干扰效果,是下一步研究的重点。
[1]保铮,邢孟道,王彤.雷达成像技术[M].北京:电子工业出版社,2005.
[2]吴晓芳,代大海,王雪松,等. 合成孔径雷达电子对抗技术综述[J].信号处理,2010,26(3): 424-435.
[3]ZhouF,ZhaoB,TaoML,etal.Alargescenedeceptivejammingmethodforspace-borneSAR[J].IEEETransactionsonGeoscienceandRemoteSensing,2013,51(8): 4486-4489.
[4]李 田,彭世蕤,王广学,等.基于幅度调制的SAR相干压制干扰方法[J].现代雷达,2014, 36(5):20-25.
[5]蔡幸福,宋建社,郑永安,等.二维间歇采样延迟转发SAR干扰技术及其应用[J].系统工程与电子技术,2015,37(3):566-571.
[6]MehrdadSoumekh.SAR-ECCMusingphase-perturbedLFMchirpsignalsandDRFMrepeatjammerpenalization[J].IEEETrans.onAerospaceandElectronicSystems,2006, 42(1):191-205.
[7]李江源,王建国.利用复杂调制LFM信号的SAR抗欺骗干扰技术[J].电子与信息学报, 2008,30(9):2111-2114.
[8]冯祥芝,许小剑.随机线性调频斜率SAR抗欺骗干扰方法研究[J].系统工程与电子技术,2009,31(1):69-73.
[9]杨伟宏,刘进,王涛.SAR间歇采样散射波干扰[J].宇航学报,2012,33(3):367-373.
[10]张静克,代大海,邢世其,等.对调频斜率极性捷变SAR间歇采样转发干扰效果分析[J].系统工程与电子技术,2015,37(5):1030-1034.
[11]黄洪旭,黄知涛,周一宇.对合成孔径雷达的移频干扰研究[J].宇航学报,2006,27(3):463-468.
[12]黄洪旭,黄知涛,周一宇.对合成孔径雷达的随机移频干扰[J].信号处理,2007,23(1): 41-45.
[13]黄洪旭,黄知涛,吴京,等.对合成孔径雷达的步进移频干扰[J].宇航学报,2011, 32(4): 888-902.
[14]王玉军,赵国庆.对LFM雷达的N阶SSC盲移频干扰算法[J].电路与系统学报,2011, 16(4):70-74.
Blind Shift-frequency Jamming for SAR Based on Spectrum Spread
FANG Mingxing, BI Daping, SHEN Aiguo
(Electronic Engineering Institute, Hefei Anhui 230037, China)
The traditional shift-frequency jamming is invalid for waveform agile SAR, so a new method of shift-frequency jamming was brought forward for SAR: blind shift-frequency jamming for SAR based on spectrum spread. The spectrums of two channel signals were expanded, and then the two channel signals were compressed to generate jamming signal. The signal of spectrum spread is restored to original form of SAR echo, and an additional modulation phase was added to the frequency-shift jamming signal, so it could produce fronted and lagged false targets in the range direction. This method did not need to know the frequency modulation slope information, and it provided a new feasible approach against waveform agile SAR, so it’s a blind shift-frequency jamming method. Theoretical analysis and computer simulation results justified the validity and efficiency.
synthetic aperture radar;spectrum spread;spectrum compression;blind shift-frequency jamming
2016-01-21
房明星(1988—),男,安徽蚌埠人,博士研究生,研究方向:SAR信号处理及SAR对抗理论。E-mail:mingxingfang89@163.com。
TN974
A
1008-1194(2016)04-0096-07
