负载下外包钢筋混凝土加固轴压钢柱承载力计算方法

万路霞, 周　乐, 伊军伟

(沈阳大学 建筑工程学院, 辽宁 沈阳　110044)



负载下外包钢筋混凝土加固轴压钢柱承载力计算方法

万路霞, 周乐, 伊军伟

(沈阳大学 建筑工程学院, 辽宁 沈阳110044)

在合理基本假设下,对负载下钢筋混凝土加固钢柱的折减系数进行修改,求解轴压加固柱的承载力公式.并通过试验,分析验证混凝土强度、初始负载量、配箍率等对折减系数的影响.结果表明,适当的混凝土强度既能提高柱承载力又能使钢筋刚好屈服;初始负载量越小,加固柱的承载力提高越明显;试验中配箍率高的加固柱延性较好.最后将推算结果与规范和实验结果对比,规范中钢筋与混凝土两部分的折减系数均取0.8,过于保守,而推算公式计算结果更贴近试验结果,相对合理些.

负载; 钢筋混凝土外包; 轴压钢柱; 承载力; 折减系数

建筑物遭到偶然或自然的破坏,或者原有结构功能、使用功能已经不能满足使用要求,大部分使用者首先想到的是加固结构构件,因为推倒重建会提高工程造价,造成不必要的浪费,故结构构件加固已经成为普遍的方法.钢柱有很多种加固方法[1-2],如增大截面法,FRP布粘贴法,粘贴角钢加固法,等等,外包混凝土属于增大截面法.

因为20世纪我国钢材资源匮乏,导致钢结构发展也相对落后.为此,我国参照国外规范,摸索出一系列适合国内的规范,如《钢结构加固技术规范》《建筑结构鉴定与加固改造技术的进展》等,但在近几年的求证过程中发现，规范中负载下加固轴压钢的承载力计算,方法过于保守[3].

1　基本假设

由于加固柱在实际中受力情况比较复杂,存在外界干扰、施工技术等因素,且钢筋混凝土的变化也没有那么理想,因此在理论分析时做出以下基本假设:

(1) 受力平截面的应力变化符合平截面假定.

(2) 钢筋和型钢在达到屈服前,应力均为其线应变与其相应弹性模量[4]的乘积.

(1)

式中:σs、εs为钢材的应力、应变;Es、fy、εy为钢材的弹性模量、屈服强度、屈服应变.

(4) 原型钢柱不发生局部屈曲.

(5) 型钢与混凝土间黏结性能较好,受力过程中不发生相对滑移.

2　加固柱承载力计算

负载下加固的钢柱不同于一次性整浇钢骨柱,也与完全卸载下加固柱受力有所不同.轴心受压原柱在加固前已经产生应变,新浇混凝土的应变落后于原柱型钢的变形,即产生应变滞后现象,随着轴力的增加,型钢逐渐达到屈服应力,不再承受载荷,只发生形变,所有载荷由钢筋混凝土柱承担,至型钢变形极限应变,外包混凝土被压碎,柱子失去承载能力,破坏.根据基本假定,加固新柱从开始受力至破坏,混凝土与钢柱都保持良好的黏结性能,型钢、混凝土、钢筋三者发生相同的变形量.我国混凝土加固规范,对负载下钢筋混凝土外包钢柱的应力滞后问题,考虑了外包部分的折减系数,但将钢筋和混凝土两部分的折减系数同取0.8[4],忽略了部分材料特性,如混凝土的强度、钢筋强度、外包截面面积等.由以往实验研究可以看到,这些因素或多或少都影响着加固新柱的承载力大小.参阅了大量文献及做了相关试验[6]后,本文对加固柱新的轴向承载力做了如下修改:

(2)

(3)

(4)

式中:Fssu为原柱破坏时的极限承载力设计值;σss1为原柱加固前的在已存在载荷下的应力值;Ass为钢柱的有效截面面积;β为型钢初始负载应力水平指标.

混凝土达到屈服前应力应变关系为式(5):

(5)

(6)

(7)

式中:σc、εc分别为加固混凝土抗压应力、应变值,εc o为混凝土应力值达到Fc时对应的应变量,一般取0.002;Δεss为原柱从加固至破坏时的形变量;Ess、Es分别为型钢、钢筋的弹性模量;σs为钢筋的抗压应力.

当β=0时,αc=αs=1,加固柱的承载力计算见式(8):

笔者在上文列举的合法性标准、有效性标准、目标性标准、效率性标准、时限性标准、统合性标准、回应度标准、影响力标准、社会价值观标准、可持续发展标准，全方位的评价了社会福利政策过程，可以作为参考。

(8)

由式(8)可以看出,完全卸载时相当于一次整浇型钢混凝土柱;另外β值愈小或卸载量越大,加固柱的承载能力愈大,当β值取1时,表示原柱在加固前就开始屈服,此时已经不用再加固了,因此构件加固前应尽量卸载.

在轴压加固柱受力过程中,箍筋对核心混凝土具有约束作用,所以混凝土为加固柱提供的承载力有两部分,一部分是自身抵抗力,一部分是箍筋给予的[7-8].Mander[9]提出了箍筋的约束模型,针对这一加固方法推导出箍筋约束混凝土的承载力如式(10).

(9)

(10)

(11)

(12)

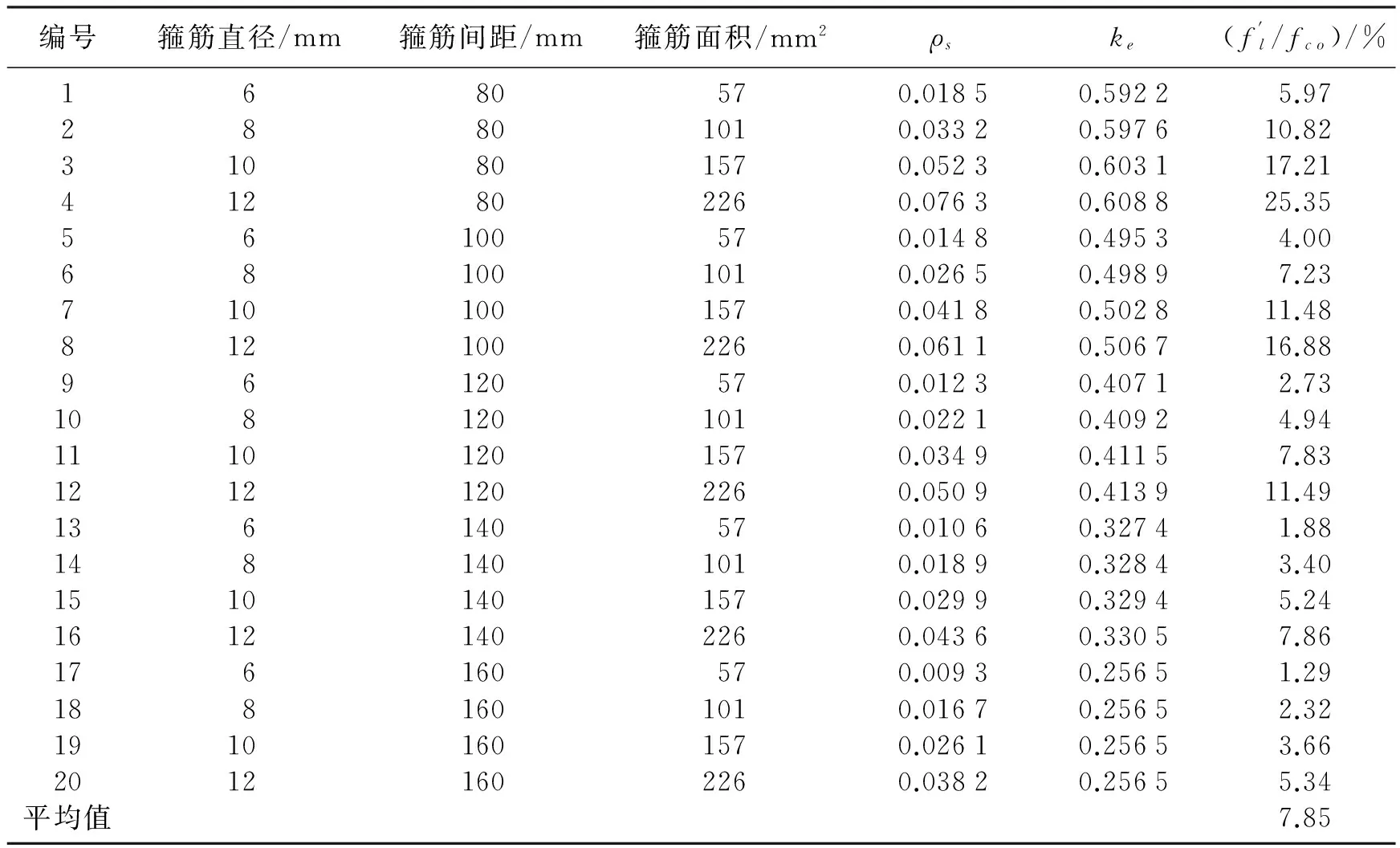
表1　具体的验证数据

3　影响承载力大小的因素

针对钢筋混凝土外包加固形式,对持载型钢柱进行加固实验.试验时对加固柱进行轴压,根据钢骨规范,试验中型钢均采用热轧Q235级工10(100×68×4.5×7.6)碳素钢;纵向钢筋采用4∅14的HRB335级钢筋,加固后柱的截面尺寸为200 mm×200 mm,加固柱的正截面形式如图1所示;柱子高度为1.2 m,共做了7根加固柱,具体参数如表2所示.

图1　构件截面尺寸及配筋(mm)Fig.1　Sectional dimensions and reinforcement details of specimens 表2　试验主要参数 Table 2　The main parameters of test

构件编号柱高/mmL/mmHu/mmN0/kN混凝土/MPa型钢/mm纵向钢筋/mm箍筋/mmSRHC-11200200200—C60I10146.5SRHC-212002002000.3NuC60I10146.5SRHC-312002002000.5NuC60I10146.5SRC-412002002000.3NuC40I10146.5SRHC-512002002000.3NuC80I10146.5SRHC-612002002000.3NuC60I10148.0SRHC-712002002000.3NuC60I101410.0

注:L为被加固柱截面宽度,Hu为被加固柱截面高度,Nu、N0分别为钢柱轴压承载力、负载下外包钢筋混凝土加固时钢柱的初始轴压力.

3.1初始负载对承载力的影响

从表1可知,SRHC-1、SRHC-2、SRHC-3三根柱子的初始负载不同,分别为0、0.3Nu、0.5Nu.由式(6)、式(7)可以看出,β值越大,折减系数越小,即钢筋混凝土两部分分担点承载力越少,原钢柱过早屈服,将起不到加固效果.β值与折减系数成反比,越小越好,故建议实际工程中,尽量卸载,充分发挥材料性能.图2能较好地反映初始负载与折减系数之间的关系.

3.2混凝土强度对承载力的影响

从试验参数表2可知,试验过程中采用了三种混凝土强度:C40(SRC-4)、C60(SRHC-2)、C80(SRHC-5).仅从折减系数公式来看,同一配筋率、相同截面面积的构件,混凝土强度对折减系数基本无影响;从图3可以看出,随着混凝土强度的提高,构件材料的应变逐渐减小;从试验现象知,加固柱SRHC-5破坏时纵向钢筋仍未屈服,纵筋强度没有得到充分利用,承载力计算公式的假设条件为:三者有相同的形变量,加固材料应力达到屈服点,由此计算加固柱的承载力将大于试验值.

图2　轴心受压钢柱αs、αc和β的关系Fig.2　αs,αc and β curve of axial compression reinforced column

图3　混凝土强度等级-应变曲线Fig.3　Grade-strain curve of concrete strength

3.3配箍率对承载力的影响

从目前文献知,配箍率对折减系数影响的研究还是很少,许鹏红[8]对此作了部分试验研究,笔者考虑到箍筋对混凝土具有部分约束作用,于是将混凝土的承载力分了两部分:一部分为混凝土不被箍筋约束仅靠自身能力提供的抗力;一部分为仅被箍筋约束时,箍筋给予的结构抗力.

箍筋可以对纵向受力钢筋定位,也可以约束混凝土的侧向变形.当加固柱达到屈服载荷时,原钢柱承载力不再增加,载荷由混凝土部分承担,但位移形变量仍在继续增加,混凝土受到三部分作用,一部分为轴压荷作用,另一部分为型钢变形时的挤压,再一部分就是外部箍筋的约束.混凝土处于三面受力,此时箍筋对内部混凝土约束则显得尤为重要,提高了柱子的延性.试验中,SRHC-2、SRHC-6、SRHC-7构件的箍筋直径分别为6.5、8、10 mm,混凝土强度、截面面积等其他条件相同.实验现象表明,随配箍率的增大,混凝土截面轴向位移逐渐增大,延缓了型钢的应变增长速度,使得加固柱的整体延性提高.

4　实验结果与理论结果对比分析

根据式(2)及《钢结构加固技术规范》:CECS 77:96,与实验结果进行比对,具体见表3.

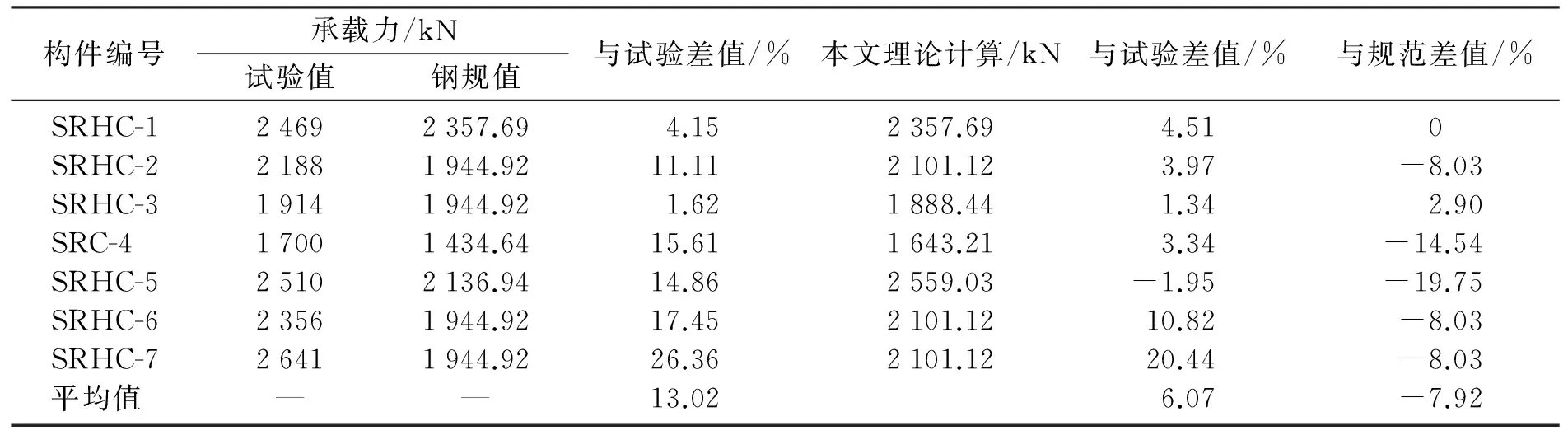
表3　加固柱承载力结果对比表

由表3可知,钢结构加固规范与推导公式相比,最大值相差20.44%,最小值相差1.34%,平均值6.07%,结果总体上低于试验值,且相差不多,计算结果较安全;试验值对比规范,平均差值为14.45%,所以αc=αs=0.8,过于保守,加固材料得不到充分利用;另外,试验值总体低于推算公式结果,平均差值为-7.92%.试验现象表明,箍筋提高了加固柱的延性,由于箍筋直径相差不大,计算时将箍筋约束混凝土的有效面积取同一数据,才使得计算结果一样,但对比SRHC-3构件可以看出,箍筋发挥了部分作用;规范中未体现箍筋作用,总的来说,该推导公式计算结果接近但低于试验值,偏于安全,比规范较合理.

5　结　　论

(1) 仅运用我国钢结构加固技术规范来计算加固柱的承载力,钢筋与混凝土部分的折减系数均取0.8,过于保守,且材料特性不能充分利用,造成浪费.

(2) 在合理的基本假定下,原柱和钢筋从加固至破坏均与混凝土保持良好的黏结性能,所以型钢的形变量与钢筋、混凝土的形变量相同,根据这一结果推算出钢筋混凝土两部分的折减系数.

(3) 本研究表明,初始负载量直接影响着加固柱的承载力,初始负载越大,原柱屈服越早,且承载力下降,因此应尽量卸载加固;混凝土强度越高,加固的承载能力将相对提高,但强度过高,受力纵筋达不到屈服柱子就被破坏;试验采用三种直径的箍筋来计算不同配箍率,对加固柱承载力的影响,规范未能体现箍筋的作用,所以本文推导公式更合理些.

[1] 周乐,聂晓梅,王元清,等. 负载下外包钢筋混凝土加固钢柱轴压性能试验研究[J]. 建筑结构学报, 2015(S1):275-284.

(ZHOU L,NIE X M,WANG Y Q, et al. Experimental study of axial compression behavior on steel columns strengthened by enclosed reinforced concrete under load[J]. Journal of Building Structures, 2015,36(S1):275-284.)

[2] 周乐,聂晓梅,伊军伟,等. 持载下外包混凝土加固轴压钢柱的承载力分析[J]. 沈阳大学学报(自然科学版), 2016,28(1):61-68.

(ZHOU L,NIE X M,YI J W,et al. Capacity on axial compression of steel columns strengthened by enclosed concrete under sustained load[J]. Journal of Shenyang University(Natural Science), 2016,28(1):61-68.)

[3] 聂晓梅. 负载下外包钢筋混凝土加固轴压钢柱力学性能试验研究[D]. 沈阳:沈阳大学, 2016.

(NIE X M. Experimental research on mechanical properties of axially loaded steel columns strengthened by enclosed reinforced concrete while under load[D]. Shenyang:Shenyang University, 2016.)

[4] 钢结构加固技术规范:CECS 77:1996[S]. 北京:中国计划出版社, 2005.

(Technical specification for strengthening steel structures:CECS 77:1996[S]. Beijing:China Planning Press, 2005.)

[5] HOGNESTAD E,HANSON N W,MCHENRY. Concrete stress distribution in ultimate strength design[J]. Journal of the American Concrete Institute, 1955,52(12):455-480.

[6] 周玲,陈明中,陈龙珠. 外包混凝土加固轴心受压钢柱中强度折减系数分析[J]. 建筑技术, 2005,36(2):116-117.

(ZHOU L,CHEN M Z,CHEN L Z. Analysis on strength reduction coefficient of axial loaded steel column with RC enclosure[J]. Architecture Technology, 2005,36(2):116-117.)

[7] 贾金青,姜丽君. 配箍率对SRHC短柱延性的影响[J]. 工业建筑, 2002,32(9):21-23.

(JIA J Q,JIANG L J. Influence of stirrup ratio on displacement ductility of steel reinforced high-strength concrete (SRHC) short columns[J]. Industrial Construction, 2002,32(9):21-23.)

[8] 许鹏红. 核心型钢混凝土柱轴压性能试验研究[D]. 广州:华南大学, 2013.

(XU P H,Experimental study on axial compression performance of core steel reinforced concrete columns[D]. Guangzhou:Huanan University, 2013.)

[9] Mander J B,Priestley M J N,Park R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988,114(8):1804-1826.

【责任编辑: 祝颖】

Bearing Capacity Calculation Method of Axially Loaded Steel Columns Reinforced by Enclosed Concrete under Loading

WanLuxia,ZhouLe,YiJunwei

(Architectural and Civil Engineering College, Shenyang University, Shenyang 110044, China)

In reasonable basic assumptions,the reduction factor of loaded concrete reinforcing steel columns is modified, to solve the capacity formula under axial compression. The impacts of concrete strength,initial load, stirrup rate for reduction coefficients are analyzed by experiment. The results show that, the proper strength of concrete can not only improve the load-carrying capacity but also make the rebar just yield; the smaller the initial load is, the more obvious the improvement of the bearing capacity of the column is; Test of high rate of reinforcement in reinforced column ductility is better; the reinforced column with high stirrup has better ductility. The calculated results are compared with the specification and the experimental results. The reduction coefficients of the specification in two parts of concrete reinforcing steel column are both 0.8, which are too conservative. The results of calculated formula are closer to the experimental results,and are relatively reasonable.

under load; enclosed reinforced concrete; axially loaded steel columns; bearing capacity; reduction coefficients

2016-04-07

国家自然科学基金资助项目(51408371); 辽宁省自然科学基金资助项目(2014020098); 沈阳市计划项目(F14-196-4-00).

万路霞(1990-),女,山东菏泽人,沈阳大学硕士研究生; 周乐(1978-),女,辽宁营口人,沈阳大学教授,博士后研究人员.

2095-5456(2016)04-0320-05

TU 392

A