立足思维方法，促进认知生长<br/>——基于数学思维方法的生长性课堂研究与实践

立足思维方法，促进认知生长
——基于数学思维方法的生长性课堂研究与实践

2016-09-15江苏张家港市万红小学215600钱越胜

小学教学参考 2016年23期

关键词：体积建模生长

江苏张家港市万红小学（215600）钱越胜

立足思维方法，促进认知生长
——基于数学思维方法的生长性课堂研究与实践

江苏张家港市万红小学（215600）钱越胜

课程改革强调学生核心素养的培养。作为数学学科，学生核心素养培养的关键是数学思维方法的训练。通过引导学生观察与实验，鼓励学生猜想，开展建模活动，促进学生认知的生长和素养的提升。

思维方法认知生长

随着课程改革的深化，“核心素养”被越来越多的提起，对于小学数学而言，学生的核心素养该如何培养呢？笔者认为，对于小学数学学科而言，学生的核心素养的养成和认知的生长应该立足于数学思维方法，那么，小学数学涉及哪些常见的数学思维呢？又该如何利用？

一、引导观察与实验，体验获知的快乐

学生的数学思维往往需要外部的感官刺激来激发，“观察”和“实验”是最为常见的形象思维方式，前者是一种具有目的性的知觉活动，但仅仅将看到的结果进行阐述，那不是数学思维，因为看到的结果不一定“真实”，观察并将现象与原有的数学认知相联系，并进行“验证”才能体现出较高的思维水平；与“观察”相比，“实验”中也有观察，两种思维的差异性在于，后者更注重观察条件的人为创设性。

例如，教学“两点之间线段最短”后，可立足于学生的“观察”思维，给学生提供具有情境化的“老虎抓狐狸”图片（如图1所示），要求学生观察后思考哪条路最短。

图1　判断最短路线

设计意图：这个活动分为2个阶段，首先学生观察并形成初步印象，然后思考验证的方法，有学生想到了用尺去量，也有学生想到了用细线先沿着轨迹摆放，然后再量，学生均能够充分调动思维，即观察→判断→验证。通过这一过程，学生对“两点之间线段最短”的印象变得更为深刻。

又如，为了让学生深刻理解“三角形具有稳定性，而四边形不具有稳定性”，可以通过实验让学生自己去感悟，实验活动如图2所示。

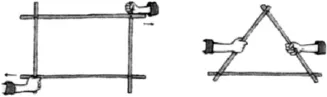
图2　三角形的稳定性

在小学数学课堂中运用实验，不但能有效提升学生学习数学的积极性，学生还能积累数学学习的经验，同时充分体验到学习数学的快乐，在观察和实验的活动中逐步接近数学问题的实质。

二、鼓励猜想，放飞创新的翅膀

新课程强调学生创新能力和创新意识的培养，“猜想”则是创新的生长点。回顾传统的灌输式教学，课堂上都是教师将正确的数学结论和方法教给学生，学生被动地接受，整个学习过程毫无意外和猜测，自然也就没有创新。

数学家高斯曾经讲过，他的许多结论都是归纳后猜测出来的，以后的证明只不过是补行手续而已。当然，对于小学阶段的学生而言，让他们猜想则容易出现胡思乱想，怎么办？给予必要的提示，让其猜想有理论和数学知识的支撑。

例如，教学“圆柱的体积”时，教师可引导学生自主猜想，并说一说猜想的依据，让学生从“长方体、正方体的体积”出发，猜想圆柱体的体积公式。（学生猜想的思维过程如图3所示）

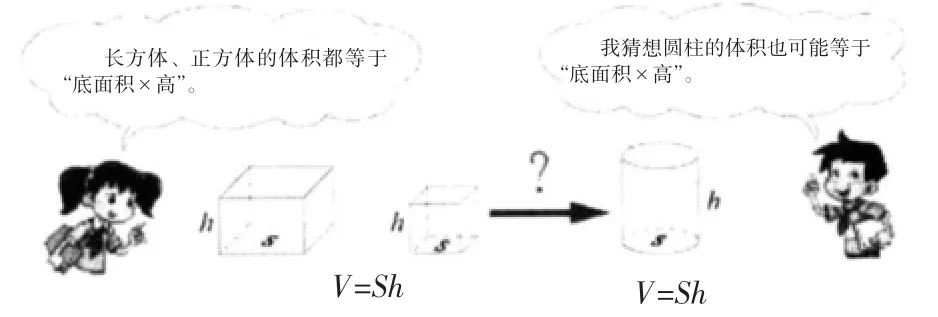
图3　猜想圆柱的体积怎样计算

猜想并非单一的思维环节，一个完整的猜想，应该包含“猜想—验证”这两个环节。

那么，对于学生猜想的这个圆柱体的体积公式应该如何去验证呢？学生有没有经验和方法呢？在找验证方法的环节，可以让学生充分讨论和合作交流，可以将学生的思维引向熟悉的情景。

验证1：堆硬币（如图4所示）。1个硬币的体积记作V，2个硬币的体积就是2V，3个就是3V，以此类推，将硬币叠放起来后底面积不变，高由h变为2h、3h......由此可以验证前期的猜想正确。

图4　

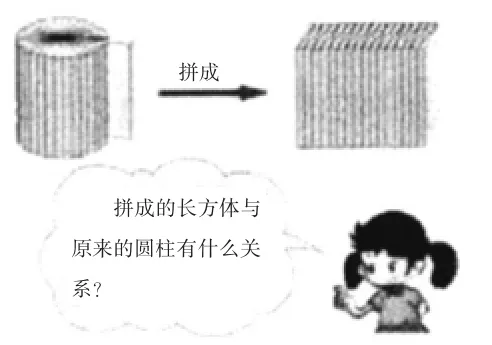
图5　

验证2：借助于“实物模型”。用一个个薄长方体拼成圆柱体，再拼成长方体，让学生观察并验证前期的猜想。

上述两种方法都体现了较高层次的数学思维方法——微元法。（小学阶段不要给这个概念，但是却可以渗透这种思维）

总之，数学教学不应该束缚学生的思维，应该尽可能地放飞学生思维的翅膀，让其进行有根据的猜想，从而实现思维的飞跃。

三、引导建模，促进解决问题能力的生长

数学学习的目的最终还是为了解决问题，发展学生解决问题的能力，而现实生活中的数学问题是真实化、情境化的，并非数学习题。此时，教师在教学过程中就要渗透“建模”的思维。因为建模是建立数学模型的过程，是一种重要的数学思维方法，数学模型是对生活中的数学问题的一种数字化、符号化或图形化的抽象，从数学关系的角度反映和刻画了数学问题的本质属性。

例如，设计合适的包装方式。如图6所示的糖果，想将两盒这样的糖果包装成一包，怎样包装才能节约包装纸呢？（接口处忽略不计）。