在变与不变中理解“倍”的实质<br/>——“倍的认识”教学实践与思考

在变与不变中理解“倍”的实质
——“倍的认识”教学实践与思考

2016-09-15江苏苏州工业园区东沙湖学校215021应秀峰

小学教学参考 2016年23期

关键词：实质小棒苏教版

江苏苏州工业园区东沙湖学校（215021）应秀峰

在变与不变中理解“倍”的实质
——“倍的认识”教学实践与思考

江苏苏州工业园区东沙湖学校（215021）应秀峰

“倍”概念的认识，是一个操作中的理解和理解中的操作、表述中的理解和理解中的表述的过程，是一个变化中有不变、不变中有共变的过程，是一个帮助学生逐渐抽象、领悟实质的过程。学生正是在不断地对比与抽象中把握了“倍”的概念，理解了“倍”的实质。

变与不变几何直观函数思想核心素养倍

“倍的认识”是“数与代数”领域中的一节概念课。数学概念的“倍”是两数比较的一种关系，是在比较多少的数量关系认识基础上的一次飞跃。学生在生活中接触“倍”的机会很少，认识“倍”的渠道也很狭窄，缺少“倍”的准确表象，而“倍”的概念又相对比较抽象，再加上学生容易受两数相差关系的干扰，其教学难度之大显而易见。课堂教学中，以哪种操作素材和什么样的操作要求引领学生进行数学活动呢？以什么样的变式学习拓展学生的思维宽度呢？以什么样的方式使抽象的概念直观化、形象化、简约化，适合学生的学习呢？这些问题的有效解决，将是教学“倍”的重点和难点。基于函数思想的理解，“倍”表示两个集合之间相对应的关系——一个和多个的关系，体现函数中“共变”现象与“变中有不变”的思想方法。因此，要理解“倍”的实质，就要研究“倍”的“共变”现象和“变中有不变”的思想。

一、用“变与不变”的观点解读教材内容，架构“倍”的框架

横向比较人教版和苏教版数学教材中有关“倍”的内容编排，发现共同之处都是在学习乘法之后认识“倍”，例题呈现的都是几倍（如3倍、4倍、5倍等）的内容，不仅创设了“小兔吃萝卜”“小朋友数花”等情境，而且提出了三种物品在数量上有什么关系的问题，把学生的思考引向两个数量之间的比较，并顺学而导，抽象出用除法解决“一个数是另一个数的几倍”的问题。纵向比较2002版数学实验教科书和2013版义务教育教科书的苏教版数学教材，发现两个版本教材的主题图相似。如2013版数学教材增加了“你能比一比这三种花的朵数吗”的内容，从两数相差关系引入，引导学生进一步学习两数的倍比关系，便于学生把“倍”的认识放在两个数量关系的整体知识体系中，完善自身的结构性知识；增加了“红花的朵数是蓝花的几倍？先圈一圈，再填一填”的内容，使学生明确圈、填的操作指向；增加了“蓝花有2朵”的内容，使学生对“倍”的语言表述更加严谨、准确。

对人教版和苏教版两个版本教材的横向比较及数学实验教科书与苏教版教材的纵向比较之后，为了让学生能从源头上感受“倍”的意义，我设计了以下的三大框架：标准量不变，比较量变化，引起倍数的变化；比较量不变，标准量变化，引起倍数的变化；倍数不变，标准量和比较量的“共变”现象。

二、在学情调研中了解“倍”的学习起点，酝酿“倍”的教学设计

设计简单的学情调研单，同时提出以下两个常见的问题：（1）听说过“倍”吗？如果你没有听说过“倍”，请在（）里打“√”；如果你听说过“倍”，那知道“倍”是什么意思吗？请列举一个或多个例子。（2）关于“倍”，你想了解什么？请写出来。

从学情调查中可以看出，学生对“倍”的概念接触较少，几乎没有任何经历和体验，再加上“倍”的概念比较抽象，所以“倍”的学习对学生而言难度较大。但从第（2）个问题去看，学生对“倍”了解的越少，也就越想揭开“倍”的神秘面纱，探究的欲望更强烈。那么，如何将“倍”的学习变成学生看得见、摸得着、能理解的数学事实呢？如何精选不同的学习素材，让学生通过有效的操作、思考、辨析，在变与不变之中理解“倍”的实质？

三、在操作素材的甄选与变更中提高操作时效，理解“倍”的内涵

1.操作素材的甄选

选择怎样的学习素材更符合学生的认知特点？“倍”的教学经历数次变化，前几次都是尊重苏教版教材的编排，采用例题中的情境，用多媒体动画呈现，引导学生在圈圈、填填、算算中学习“倍”，但是学生的语言表述是生硬的，对“倍”的理解也比较浅显。可见，这样的学习仅是表面上的理解。后几次的教学，让学生用小棒操作，以三根小棒为一份摆一摆，学生多样化的操作（如下图）令人眼前一亮，如有摆成三角形的，有三根小棒紧挨着摆的，也有将小棒分开排列的。

图①　

图②

图③

这里把三根小棒看作一份，学生会很自然地想到一个整体，也从心理上认同为一份，并能自主形成一份的表象，然后建立两份、三份的表象，最后在学生的脑海里形成两倍、三倍的直观模型。正是基于学生已有的经验，我才把学习素材改成小棒，并在学生建立“倍”的直观形象后，进一步展示彩带、线段、樱桃、草莓、圆片等多种素材，促使学生的关注点落在两个量的比较上，让学生经历从具体到抽象的过程，帮助学生理解和感悟什么是“倍”。

2.操作层次的递进

有了操作素材的比较、确定后，在操作层次上遵循由简单到复杂的规律，层层深入，环环紧扣，引导学生逐步建构“倍”的表象，逐渐抽象出“倍”的概念，理解“倍”的内涵，把握“倍”的实质。

第一层次：标准量不变，比较量变化，引起倍数的变化。

（1）如图④，师生共同摆小棒，唤醒1份的经验，认识1倍。

（2）如图⑤，扶放结合摆小棒，唤醒2份的经验，认识2倍。

（3）如图⑥，根据要求摆小棒，唤醒3份的经验，认识3倍。

图④　

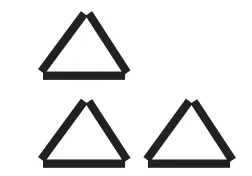
图⑤

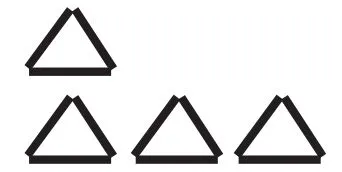
图⑥

第二层次：比较量不变，标准量变化，引起倍数的变化。

第二行的根数是第一行的（）倍

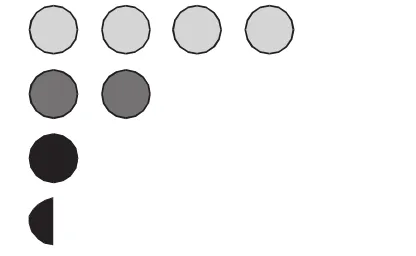
第三层次：倍数不变，标准量和比较量的“共变”现象。

在不同摆法中，凸显“倍”的实质，使学生深刻感悟：虽然学具、操作、想象等不同，但实质上是相同的，即一个数是另一个数的2倍，就有这样的2份。简单的表述，是学生对“倍”的自主理解。

（1）（）是（）的2倍。

（2）（）是（）的（）倍。

这样教学，既调动了学生思考的积极性，给予学生开放性的探究时空，又激活了学生的思维，满足了学生个性化的学习需求。

四、在“乘法倍”与“除法倍”中寻找结合焦点，沟通“倍”的联系

“乘法倍”和“除法倍”是侧重于“几个几”与“几倍”的关系，还是偏向于“份”和“倍”的关系？“乘法倍”和“除法倍”的分类不重要，重要的是“倍”的实质与内涵，强调的是概念意义的系统建构，关键是要沟通“倍”与乘除法之间的联系。在这里，“倍”与除法的关系为“平均分中的每一份同样多，有几份，就有这样的几倍”，“倍”与乘法的关系为“有几个相同的加数，就有这样的几倍”。这里面有共同的一点，即1份量是唯一的，在“倍”中1份量都是同样多的。在“倍”与乘除法的联系上，让学生对“倍”的意义进行列举、阐述，不管学生的表述是否规范或非常简略，只要是学生基于自己理解上的表述和表述中的理解即可，至于是“乘法倍”还是“除法倍”就不是那么重要了。