多级离心泵内部流动分析及性能预测

饶　昆， 聂小林，涂必成，崔宝玲

(1.浙江理工大学浙江省流体传输技术研究重点试验室，杭州 310018；2. 嘉利特荏原泵业有限公司，浙江温州 325204)



多级离心泵内部流动分析及性能预测

饶昆1， 聂小林2，涂必成2，崔宝玲1

(1.浙江理工大学浙江省流体传输技术研究重点试验室，杭州 310018；2. 嘉利特荏原泵业有限公司，浙江温州 325204)

采用Realizablek-ε湍流模型，对多级离心泵进行了CFD计算，分析了流场的分布规律和压力脉动。结果表明：由于隔舌的影响，多级泵内部各级叶轮速度与静压、总压分布均呈现非对称性；涡流、二次流等流动现象主要发生在首级叶轮蜗壳和次级叶轮蜗壳内；叶轮内叶片压力面侧进口至出口的相对速度呈现先减小后增大的趋势；隔舌处的压力脉动特性同时受到叶轮与隔舌间的动静干涉和叶片通过频率的影响。数值模拟计算得到的外性能曲线与试验的外特性曲线较吻合，误差在允许范围内。

多级泵；内部流动；性能曲线；压力脉动

0　引　言

多级离心泵是指带有多个叶轮串联安装的离心泵，因其扬程高、适用范围广、占地面积小等优点被广泛应用于石油化工、电力冷却、城市供水等多个领域。近年来，随着计算流体力学(computational fluid dynamics, CFD)的发展，利用CFD技术对泵内部流场进行数值模拟和性能预测已成为重要的研究手段[1-4]。黄思等[5]通过对多级多出口离心泵进行CFD计算，分析了不同出口设置下泵内速度和压力分布；柏占伟等[6]对离心泵内不可压缩紊流流动进行了数值模拟，分析了不同截面处的压力及速度分布并预测了其外特性；Yuan等[7]针对对称结构的双进口多级离心泵进行了数值计算，分析了扭曲叶片上的压力场和速度场；刘厚林等[8]分析了诱导轮不同时序位置对隔舌处的压力脉动影响。这些研究验证了数值计算方法能够预测多级离心泵的性能和内部流动规律。但目前，针对多级泵的研究多集中在某一级叶轮或导叶上，对其各级叶轮及蜗壳内部流场的分析还不够充分，尤其针对较为复杂结构的多级离心泵的流场分析较少[9-10]。

本文以首级双吸叶轮，次级、末级叶轮“背靠背”布置的多级离心泵为模型，采用FLUENT软件对多级离心泵进行定常及非定常的CFD计算，分析了多级泵速度、压力和湍动能分布规律，隔舌处及非隔舌处总压的压力脉动，探讨了叶轮—隔舌的动静干涉和叶片通过频率对压力脉动的影响，预测了多级泵的外特性，并与试验所得结果进行对比。本文对多级泵的水力设计和高效稳定运行具有一定的指导意义。

1　CFD计算模型及方法

1.1模型及网格

通过Pro/E软件对多级离心泵进行三维建模，其结构如图1(a)所示。泵的设计参数为：流量Q=450 m3/h，扬程H=465 m，转速n=2980 r/min。主要结构参数为：泵进口直径Di=250 mm，泵出口直径Do=200 mm。首级和次级叶轮外径D1=D2=370 mm，末级叶轮外径D3=390 mm。首级叶轮为双吸叶轮，次级和末级叶轮为单吸叶轮，各有5个叶片。数值计算过程中计算区域包括多级泵吸水室、各级叶轮流道和泵压水室的全流道。采用Gambit软件对模型泵进行网格划分，其中进出口流道采用六面体结构化网格，其他过流部件如叶轮流道等采用四面体混合网格。计算网格总数为11502181，其中首级、次级和末级叶轮网格数分别为2564969、1693715和1216865。

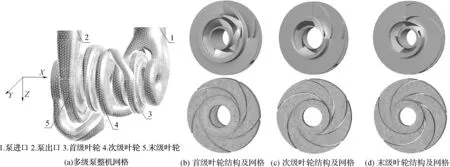
图1　多级泵整机及各级叶轮网格示意图

1.2湍流模型

标准k-ε模型用于强旋流或带有弯曲壁面的流动时，会出现一定程度的失真[11]，RNGk-ε模型对旋流、二次流等复杂流动进行了改进，提高了计算精度，Realizablek-ε模型不仅具有RNGk-ε模型的优点而且在收敛性方面更优，故本文采用Realizablek-ε湍流模型，并监视泵进出口单位面积平均总压的波动稳定情况作为辅助收敛标准。

1.3边界条件设置

工作介质为清水；进口边界给定速度进口，并根据试验环境下水的粘度和进口平均流速得到湍动能和湍流耗散率；出口边界给定自由出流；与流体接触的吸水室、叶轮和压水室等所有近壁区域均采用无滑移标准壁面函数；叶轮设置为旋转区域，且旋转的叶轮部分和静止的蜗壳部分的交界面采用滑移网格。

2　计算结果及分析

2.1速度分布及流线图

图2为额定工况时多级泵内XZ方向剖面绝对速度分布。从左至右分别为首级双吸叶轮和次级、末级单吸叶轮，由于叶轮的做功，流体的速度沿着叶轮径向逐渐增大，流体由叶轮出口进入压水室后，动压将逐渐转化为静压，故速度沿着压水室的流动方向逐渐减小。但在流体进入下一级叶轮吸水室内，由于下一级叶轮对吸水室流体的抽吸作用及流道截面逐渐减小，故沿着吸水室流体速度又逐渐增加。从图2可以看出，首级叶轮吸水室内流体流速较低，吸水室中速度分布较均匀，进入首级叶轮后，流速沿叶轮径向由5 m/s逐渐增大到45 m/s。当流体由首级叶轮排出进入压水室后，流速沿流动方向由45 m/s逐渐降低到15 m/s，说明压水室将动压转化为静压的作用比较明显，同时次级叶轮吸水室截面内流速分布较不均匀，次级和末级叶轮流道内流体的速度变化规律基本与首级相同。

1. 泵进口 2. 首级叶轮 3. 次级叶轮 4. 末级叶轮 5. 出口图2　额定工况时XZ方向剖面绝对速度分布

图3从左至右分别为首级双吸叶轮、次级和末级单吸叶轮及对应的各级蜗壳剖面图。从图3可以看出，首级叶轮下半部分的吸水室有明显涡流存在，这是由于首级叶轮左右两侧吸水室为圆环形，流体从两侧分别流入后，在每一侧将继续沿着流道分为两部分，且在吸水室下部产生碰撞，从而产生涡流。次级叶轮吸水室也产生了涡流，这是由于吸水室内引流区域设计不够合理，没有对入流进行较好的引导，导致流体碰撞壁面而产生涡流。各级叶轮出口和压水室之间都存在涡流，原因是该处附近叶轮外盖板和蜗壳内壁面间存在间隙，叶轮出口处总压高于泵腔内总压，在压差的作用下，使得流体进入泵腔内形成间隙流从而进一步产生涡流。

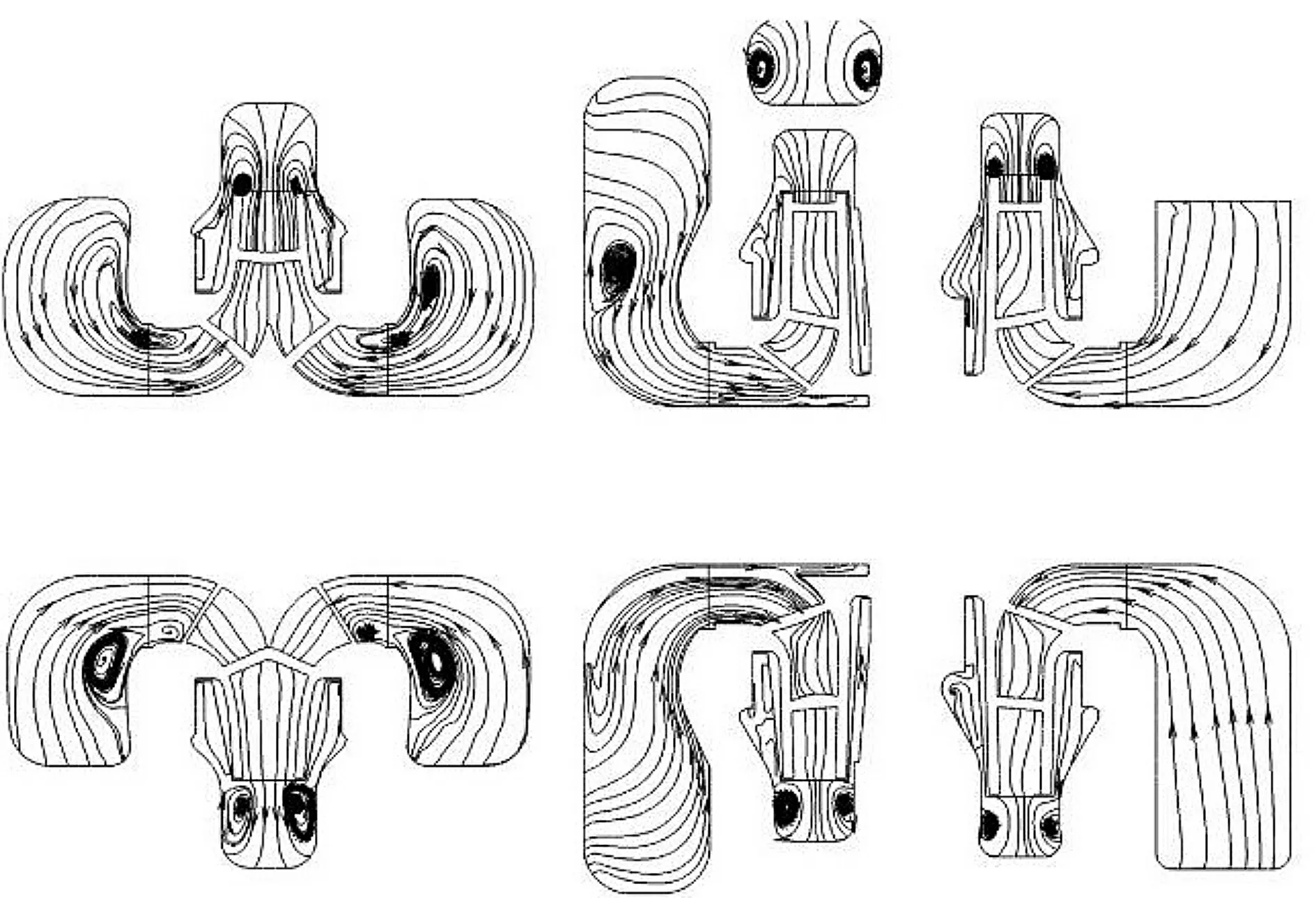
图3　额定工况时XZ剖面绝对速度流线图

图4为首级双吸叶轮、次级和末级叶轮中截面的相对速度流线图。其中首级叶轮进口处流体相对速度较低，流动较稳定，其出口相对流速较高，在叶片压力面附近易发生流动分离。流体从首级叶轮进入压水室后，压水室不能将流体的动压充分转化为静压，故次级叶轮进口处相对流速较高且不均匀，易造成流动的不稳定。同时由图4可见，叶片流道内相对速度从进口至出口呈现先增大后减小的趋势。这说明叶轮流道截面逐渐增大，对流体的扩散减速作用强于叶轮对流体的做功加速作用。末级叶轮进口处流速也较大且不均匀，分布规律和次级叶轮相似。从图4的叶轮流线图可以看出，各级叶轮流道内流线较为平稳均匀，没有明显的涡流产生，说明叶轮设计较为合理。

图4　额定工况时各级叶轮剖面相对速度流线图

2.2压力分布

图5为额定工况下多级泵内XZ剖面静压分布图。由图5可以看出，由于叶轮的旋转做功作用，叶轮内的静压沿着叶轮径向逐渐增加。进入蜗壳后，由于蜗壳的扩散作用，流体的动能逐渐转换成静压能，流体静压逐渐升高，所以静压从泵的进口到出口逐渐升高。在次级叶轮吸水室上半部分的压力分布不均匀，且存在低压区。次级叶轮进口附近静压降低，这主要是因为此处截面减小，流体速度增加，部分静压转化为动压。

图6为额定工况时叶轮中截面总压分布图。由图6可见，每一级叶轮进口处总压最低，且沿着叶轮径向总压逐渐增加，并在叶轮出口处总压最高。当流体经过蜗壳时，由于涡流和流体碰撞产生的水力损失等，总压稍有降低。从而导致流体在下一级叶轮进口的总压低于上一级叶轮出口处。首级叶轮处

出口总压约为1.5 MPa，经过蜗壳流道后，次级叶轮进口处总压约为1.4 MPa。各级叶轮蜗壳都是采用双隔舌对称分布，受隔舌处几何结构的影响，隔舌附近叶轮出口处的总压最高，且相对于其他流动区域，总压分布不均匀。

图5　额定工况时XZ剖面静压分布图

图6　额定工况时叶轮剖面总压分布图

2.3湍流动能分布

图7为额定工况时多级泵XZ剖面湍流动能分布图。湍动能的梯度大小及梯度分布所处的空间位置，在一定程度上揭示了湍流脉动的强弱和发生区域。由图7可以看出，湍动能较大的地方集中于各级叶轮的进口及其吸水室曲率较大的区域、首级叶轮的出口等，与图4的XZ剖面流线分布情况对照，发现湍动能较大分布区域基本与涡流产生的区域相同，该处速度梯度较大，流体的能量损失较多。对于叶轮的进出口区域，可能是间隙流与主流发生相互碰撞导致该处流体的速度梯度较大，对于吸水室曲率较大的区域，拐角附近流道较为狭窄，耗散率受壁面影响较大，且该处设计不够合理，没有对入流进行较好地引导，导致流体碰撞从而在内壁面产生涡流。

图7　额定工况时XZ剖面湍流动能分布

2.4非定常压力脉动分析

压力脉动分析采用流体计算软件FLUENT进行非定常计算得到，泵转速为2980 r/min，设置叶轮每转2°为一个时间步长，即Δt=1.11186×10-4s。

为了分析在叶轮旋转360°的完整周期内，多级泵各级蜗壳隔舌及叶轮的动静干涉作用，在各级蜗壳内各选取3个监测点进行分析，监测点位置如图8所示。监测点总压的压力脉动图如图9—图11所示，其中横坐标为旋转角度，纵坐标为总压值，每隔2°的旋转角度得到一个总压值，对一个完整旋转周期进行分析。

图8　多级离心泵各级蜗壳监测点位置

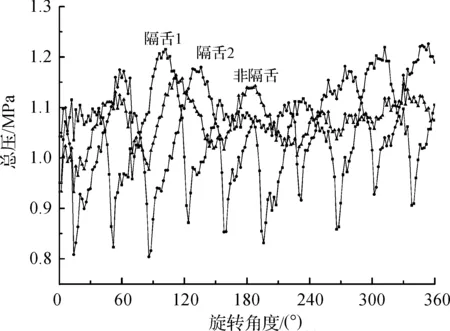
图9　首级蜗壳监测点压力脉动

图10　次级蜗壳监测点压力脉动

图11　末级蜗壳监测点压力脉动

由于首级叶轮和后两级叶轮都为5叶片，所以在一个完整周期内，各个监测的压力脉动都有5个明显的波峰，由图9—图11看出基本满足此规律，说明总压的压力脉动与叶片数有关。

由于隔舌的干涉，隔舌处总压脉动的波峰值基本都高于非隔舌处的波峰值，同时由图中看出，波峰的出现是随着叶轮与隔舌相对位置的变化而变化的，即随着叶轮旋转，波峰逐渐向右移动，在一个周期内形成循环，且各级蜗壳隔舌2处的波峰都滞后于隔舌1处的波峰1/10T, 这不仅与各级叶轮的5叶片结构以及蜗壳的双隔舌结构相吻合，也说明总压的压力脉动其时间序列与隔舌—叶轮之间的动静干涉有关。

图12—图14为各级蜗壳监测点处总压的压力脉动频域图，由压力脉动时域图经过傅里叶变换得到，其纵坐标为不同时刻下总压与整个周期平均值的差值。多级泵的叶轮转速为2980 r/min，故轴频约为49.67 Hz。由各频域图可以看出，波峰位置对应的主频主要为248 Hz和496 Hz，分别对应5倍轴频和10倍轴频，即监测点处总压脉动的主频为1倍和2倍叶片通过频率fn；各级蜗壳在fn时隔舌1和隔舌2处的总压脉动幅值几乎相同，但要高于非隔舌处，如首级、次级和末级叶轮隔舌处压力脉动幅值分别是非隔舌处的2.2倍、1.3倍和1.4倍，隔舌处压力脉动幅值几乎相同是因为采用了对称的双隔舌结构，幅值更高说明隔舌处的总压脉动受到叶片通过频率的影响要大于非隔舌处，故隔舌处的总压受到动静干涉的影响更大。

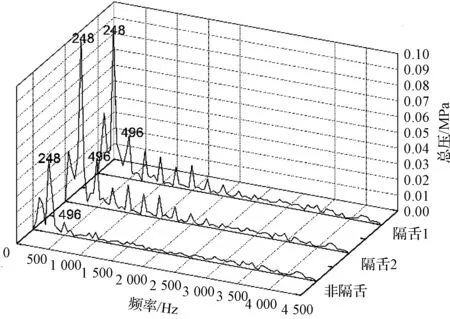
图12　首级蜗壳监测点压力脉动频域图

图13　次级蜗壳监测点压力脉动频域图

图14　末级蜗壳监测点压力脉动频域图

3　多级泵的水力性能预测和试验验证

本文将外特性试验与数值计算结果进行对比。图15为数值计算所得泵扬程、效率和轴功率曲线与性能试验结果的对比结果。设计工况点下该多级泵试验和数值计算所得到的扬程分别为475 m和474.75 m，效率分别为69.1%和69.38%，轴功率分别为850 kW和836.719 kW，且由图15可以看出，试验和数值计算所得扬程的最大误差为3.9%、效率最大误差为6.3%、轴功率最大误差为9.04%，均在10%误差范围内。同时，泵的数值计算特性曲线与试验特性曲线较为吻合，这说明了本文所用数值计算方法可行、准确。

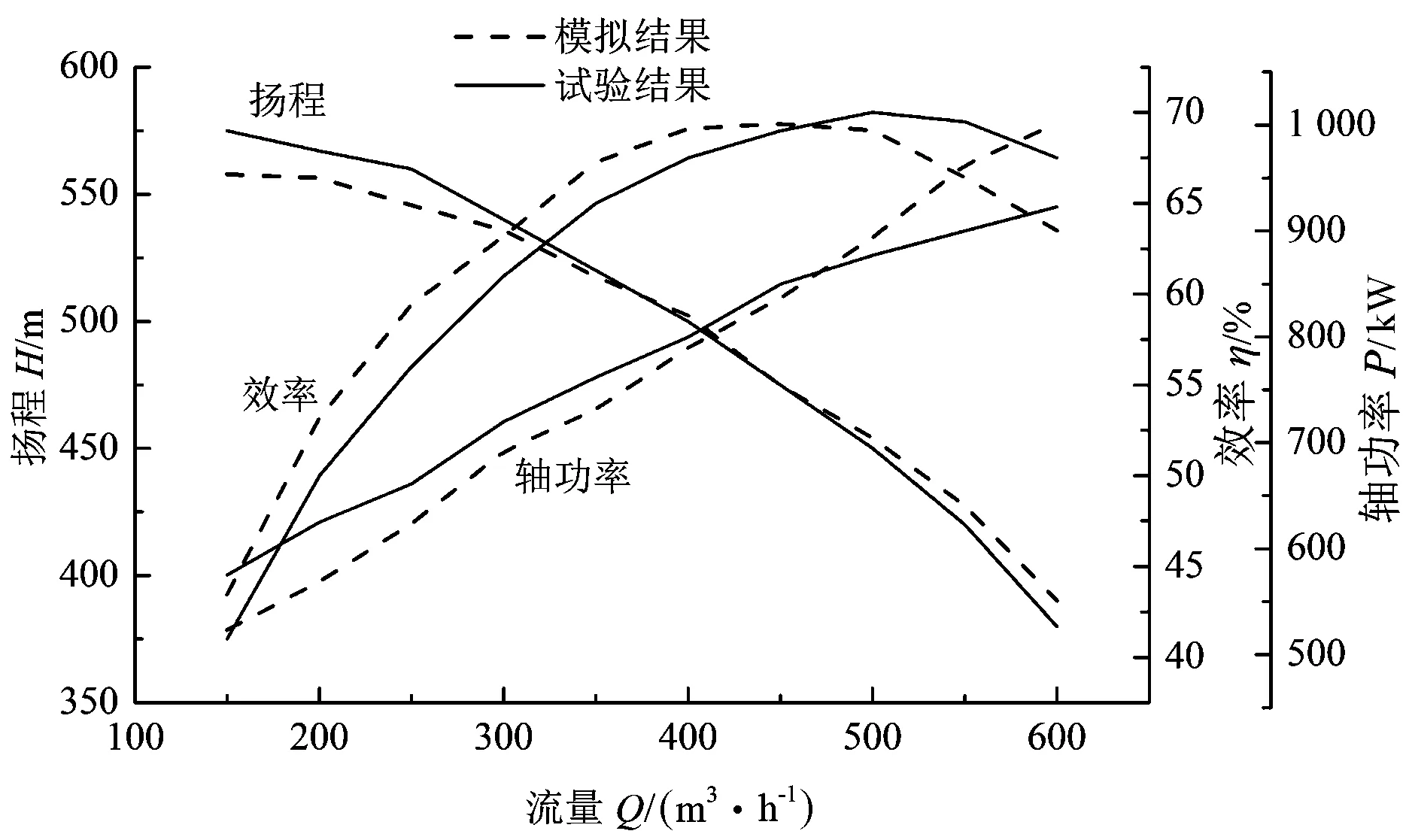
图15　试验与数值预测的外特性对比

4　结　论

本文对采用首级双吸叶轮，次级、末级叶轮“背靠背”设计的多级离心泵进行了CFD计算，分析了多级泵内部流场的速度分布、压力分布、湍动能分布和压力脉动特性；并对泵进行外特性试验，验证了数值模拟的准确性。

a)受隔舌的影响，各级叶轮速度与静压、总压分布均呈现非对称性；在首级叶轮进口叶片吸力面附近压力最低。

b)叶轮内叶片压力面侧进口至出口其相对速度呈现先减小后增大的趋势，叶轮进口处吸力面附近流速较压力面高，叶轮流道内流线分布较为均匀。涡流主要产生在首级叶轮蜗壳、次级叶轮蜗壳内和叶轮出口和压水室之间。

c) 隔舌及非隔舌处总压的压力脉动与叶片通过频率及隔舌-叶轮之间的动静干涉有关，且隔舌处的总压受到的动静干涉作用影响比非隔舌处更大。

[1] 江见福,顾伯勤,邵春雷.多级泵内部流动分析及其性能预测[J].南京工业大学学报:自然科学版，2012,34(5):94-98.

[2] HUANG S, YANG F X, GUO J. Numerical simulation of 3D unsteady flow in centrifugal pump by dynamic mesh technique[J]. Procedia Engineering,2013,61:270-275.

[3] 刘元义,王广业.低比转数冲压多级泵叶轮内三维流动数值模拟[J].农业机械学报,2006,37(11):60-63.

[4] 王志坚,佟亮,李璐璐,等.基于CFD的离心泵内部三维流动数值模拟和性能预测[J].流体机械,2012,40(6):14-18.

[5] 黄思，王朋，区国惟.多级多出口离心泵的数值模拟及试验验证[J].流体机械，2013，41(1):10-13.

[6] 柏占伟,裴江红,胡韶华.离心泵内流场的数值模拟[J].机械设计与制造,2009(6):223-225.

[7] YUAN D, WANG L. Based on fluent numerical analysis of impellers for a multi-stage water pump[C]//Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), 2011 2nd International Conference on. IEEE, 2011: 3812-3815.

[8] 刘厚林, 崔建保, 谈明高, 等. 离心泵内部流动时序效应的CFD计算[J]. 农业工程学报, 2013(14): 67-73.

[9] TVERDOKHLEB I, KNYAZEVA E, BIRUKOV A, et al. About designing the flow part of a multi-stage pump with a minimum radial dimensions[J]. Procedia Engineering, 2012, 39: 84-90.

[10] 王昌生,李志鹏,陈芳芳,等.多级离心泵首级叶轮内部流动的数值模拟[J].水电能源科学,2012,30(6):147-150.

[11] 王福军.计算流体动力学分析：CFD软件原理与应用[M].北京:清华大学出版,2004.

[12] 关醒凡.现代泵理论与设计[M].北京:中国宇航出版社,2011:18-25.

(责任编辑： 康锋)

Analysis of Inner Flow and Performance Prediction of Multistage Centrifugal Pump

RAOKun1,NIEXiaolin2,TUBicheng2,CUIBaoling1

(1. Laboratory of Fluid Transmission and Application, Zhejiang Sci-Tech University,Hangzhou 310018, China；2. Ebara Great Pump Co., Ltd., Wenzhou 325204, China)

Based on realizablek-εturbulence model, CFD calculation of multistage centrifugal pump is done and the distribution law of inner flow and the pressure fluctuation are analyzed. The result shows that because of the influence of the volute tongue, the inner flow parameters such as the distribution law of velocity, static pressure and total pressure of each impeller in the multistage centrifugal pump are asymmetrical; the vortex and secondary flow and other flow phenomena are mainly found at the first and second stage impeller volutes; the relative velocity from inlet to outlet on the pressure surface of inner blade of impeller shows the tendency of decrease first and then increase; the characteristics of pressure fluctuation at the baffle tongue are under both interference of timing effect between impeller and baffle tongue as well as the influence of passing frequency of blades. The external performance curves obtained by numerical analog computation are in agreement with the external characteristic curves and the error is within the allowable range.

multistage pump; inner flow; performance curve; pressure fluctuation

10.3969/j.issn.1673-3851.2016.05.011

2015-08-19

国家自然科学基金项目(51276172)；浙江省重大科技专项重点工业项目(2013C01141)

饶昆(1988-)，男，河南信阳人，硕士研究生，主要从事流体机械流固耦合、转子动态特性方面的研究。

崔宝玲，E-mail：blcui@zstu.edu.cn

TH311

A

1673- 3851 (2016) 03- 0385- 07 引用页码： 050403