经济型立体车库结构静力分析与优化

焦颖颖，杜小强，袁　博，林乐鹏

(浙江理工大学机械与自动控制学院，杭州 310018)



经济型立体车库结构静力分析与优化

焦颖颖，杜小强，袁博，林乐鹏

(浙江理工大学机械与自动控制学院，杭州 310018)

针对立体车库结构强度低导致安全事故频发的问题，以某公司生产的经济型立体车库为例，采用CAD/CAE技术对其结构进行静力分析与优化。首先运用SolidWorks建立了立体车库结构三维模型；然后导入ANSYS Workbench中建立有限元模型，对立体车库钢架结构进行有限元静力分析；最后对立体车库薄弱部件进行响应曲面分析，并根据分析结果优化立体车库零件。研究得到了立体车库工作时整体应力和变形的分布规律，最大应力为153.07 MPa，最大变形为10.453 mm，满足安全使用要求；优化设计后，在保证车库强度和刚度的情况下节约了2.31%的钢材量，为立体车库结构改进提供了参考依据。

立体车库；有限元；静力分析；优化设计

0　引　言

机械式立体车库作为城市现代化标志之一，具有较高的实用性和观赏性，可以缓解城市交通堵塞，改善城市环境，并能带来很高的经济效益。立体车库已在国外得到了广泛应用[1-3]，早在1920年美国就建成了世界上第一座机械式立体车库，日本是亚洲地区最早开展立体停车设备研发的国家。立体车库在亚洲的市场主要集中在日本、韩国、中国等地，而韩国和中国的停车设备技术都来源于日本[4-5]。随着经济的飞速发展，我国机械式立体车库已有较大生产规模，但利用率不高，主要原因在于：司机停车不习惯，驾车技术要求高；民众对立体车库质量认可度低。质量问题是立体车库行业发展面临的巨大挑战[6]。据2013年度中国停车设备行业年会统计，当年新取得停车设备制造许可证的企业由其他行业进入的约占7成，行业门槛较低，停车设备行业面临无序扩张。该行业各项检验标准不统一，企业追求高效生产，忽视安全指标，导致近年安全事故频发，给使用者带来重大经济损失[7]。因此，开展立体车库研究，提高立体车库安全设计、生产制造水平具有重要意义。

立体车库故障总体上分为设备自身故障、人为故障和外部影响产生的故障三大类。大多数故障与车库结构失效有直接关联，所以提高立体车库钢架结构整体的安全使用性能是降低事故率、减少损失的关键一步[6]。近几年，诸多学者在立体车库结构设计与优化方面进行了研究。徐格宁等[8-10]提出了钢结构立体停车库系统失效树理论的分析方法以及结构系统失效准则的合理性原则，又利用SAP50 软件进行分析，验证钢结构强度、刚度和稳定性。荆友录等[11]通过ANSYS软件对立体停车库钢结构骨架进行受力分析，并采用增广乘子法对车库结构进行优化。李海英等[12]通过ANSYS对立体车库进行刚度和强度分析，判断出钢架结构的危险点和危险截面。谭忠宏[13]设计了电梯式升降立体停车库的钢结构骨架，并定位出其最大应力单元和最大变形单元，验证了结构设计的可靠性。但是，对于经济型立体车库的研究鲜见报道，该类立体车库对工作环境要求低，开发难度小，国内大多数停车设备以该类车库为主，同时也是故障和事故多发的主要来源[4,14-15]。

本文通过ANSYS和SolidWorks软件，采用CAD/CAE技术对经济型立体车库进行了结构静力分析与优化。首先在SolidWorks中通过适当简化建立经济型立体车库的三维实体模型，然后导入ANSYS Workbench进行静力分析，最后通过ANSYS Workbench的响应曲面分析法来优化结构零件，在保证结构强度的前提下为立体车库结构改进提供了参考依据。

1　经济型立体车库三维建模

本文选取链条式二层升降横移立体车库作为研究对象(如图 1所示)。该类立体车库以容纳T2型车为最大容量设计，允许收容车辆参数：车长≤5200 mm、车宽≤1900 mm、含后视镜宽≤2000 mm、轮胎外宽≤1860 mm、车高≤1550 mm、车重≤2000 kg，最大存容量为5辆(上层3辆、下层2辆)。该类立体车库的设计尺寸和动态参数：整体车库尺寸7400 mm×5850 mm×2650 mm、停车尺寸2400 mm×5625 mm×1800 mm、升降速度4.0～5.0 m/min、横移速度7.0～8.0 m/min、升降电机功率2.2 kW、横移电机功率0.2 kW、升降电驱动链的型号为20 A、提升链型号为16 A。

图1　链条式二层升降横移立体车库照片

本文针对满载时链条式二层升降横移立体车库的钢架结构进行有限元静力分析。在三维建模中选用SolidWorks辅助建模，它可与有限元分析软件ANSYS Workbench实现无缝连接，提高了建模的灵活性。

在该停车设备中，钢结构架主要是由标准H型钢和口型钢构成，根据结构型材特点，部分标准型钢可利用SolidWorks中Toolbox直接插入，非标准型钢单独建模，最后将各部分零件装配完成。前横梁、后横梁和纵梁分别为300 mm×150 mm、100 mm×100 mm、250 mm×125 mm的H型钢，前立柱为150 mm×150 mm的口型钢，后立柱为100 mm×100 mm的H型钢。对模型进行了简化，省略了对钢架结构分析影响不大的构件，如：链条、接地载车板、防脱钩、电机等，在分析时二层载车板以载荷形式添加。立体车库结构三维模型如图 2所示。

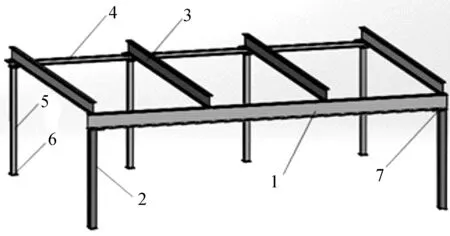
1.前横梁 2.前立柱 3.纵梁 4.后横梁 5.后立柱 6.接地板 7.连接板图2　立体车库结构三维模型

2　经济型立体车库有限元静力分析

线性静力结构分析用来分析结构在给定静力载荷作用下的响应[16]。多自由度系统的动力学方程为：

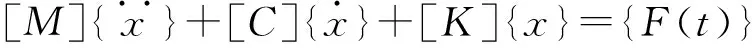
(1)

其中：[M]为质量矩阵，[C]为阻尼矩阵，[K]为刚度矩阵，{x}为位移矢量，{F}为力矢量。

线性静力结构分析是计算固定不变的惯性载荷对结构的影响，与时间无关，去除式(1)中与时间相关项可得：

[K]{x}={F}

(2)

材料需满足刚度矩阵连续、线弹性、小变形理论，力矢量与时间无关[17]。

2.1有限元模型建立

将立体车库三维模型导入ANSYS Workbench，首先在DM中对模型进行整合，使立体车库装配体模型转换为一个Part以便分析。该转换方式根据分析对象的结构特点设计。一方面，立体车库是钢架结构，构件之间通过焊接或螺栓连接，没有相对运动，把所有构件看成一体是可行的，不需要设置接触类型；另一方面，在网格划分时将以整体网格划分，不同构件连接处共节点，通过两个面共享一部分节点实现位移和力的传递。立体车库结构中还存在一些角焊连接、螺栓孔等，参考圣维南原理，细小特征对结构整体的性能影响很小，对立体车库模型中焊缝、圆角、螺栓孔等特征忽略，使模型简化以有利于提高有限元分析效率[18]。最后在纵梁上绘制受力面，为添加载荷做准备。

2.2单元选取与网格划分

所研究的立体车库结构采用Q235，其综合性能较好，是一种用途十分广泛的普通碳素结构钢。设置参数：屈服应力为235 MPa，抗拉强度375 MPa，弹性模量E=2.0×105MPa，泊松比μ=0.3，密度ρ=7850 kg/m3，模型总体质量约为1420.6 kg，根据整体尺寸设置单元尺寸控制在25 mm。由于车库零件形状规则，在ANSYS Workbench的智能网格划分方法下得到六面体单元，划分后节点为519260，单元总数为170906。

2.3载荷与约束

立体车库接地板通过膨胀螺栓固定在地面上，接地板再与前立柱和后立柱焊接，其他构件间通过螺栓固定，整体是一个稳定的钢架结构。满载时，每个上层车位允许承载2 t的车重载荷，每个载车板自重400 kg，这些载荷通过链条和滑轮直接施加在每个车位的纵梁上(下层载车板由横移地轨支撑，故立体车库满载载荷只考虑上层车位)。对立体车库的加载和约束可简化为接地板固定约束，每个车位载荷均分四份施加在纵梁提升链条处。外侧两根纵梁每个受力面加载荷5880 N，中间两根纵梁每个受力面加载荷11760 N，垂直受力面向下，如图 3所示。

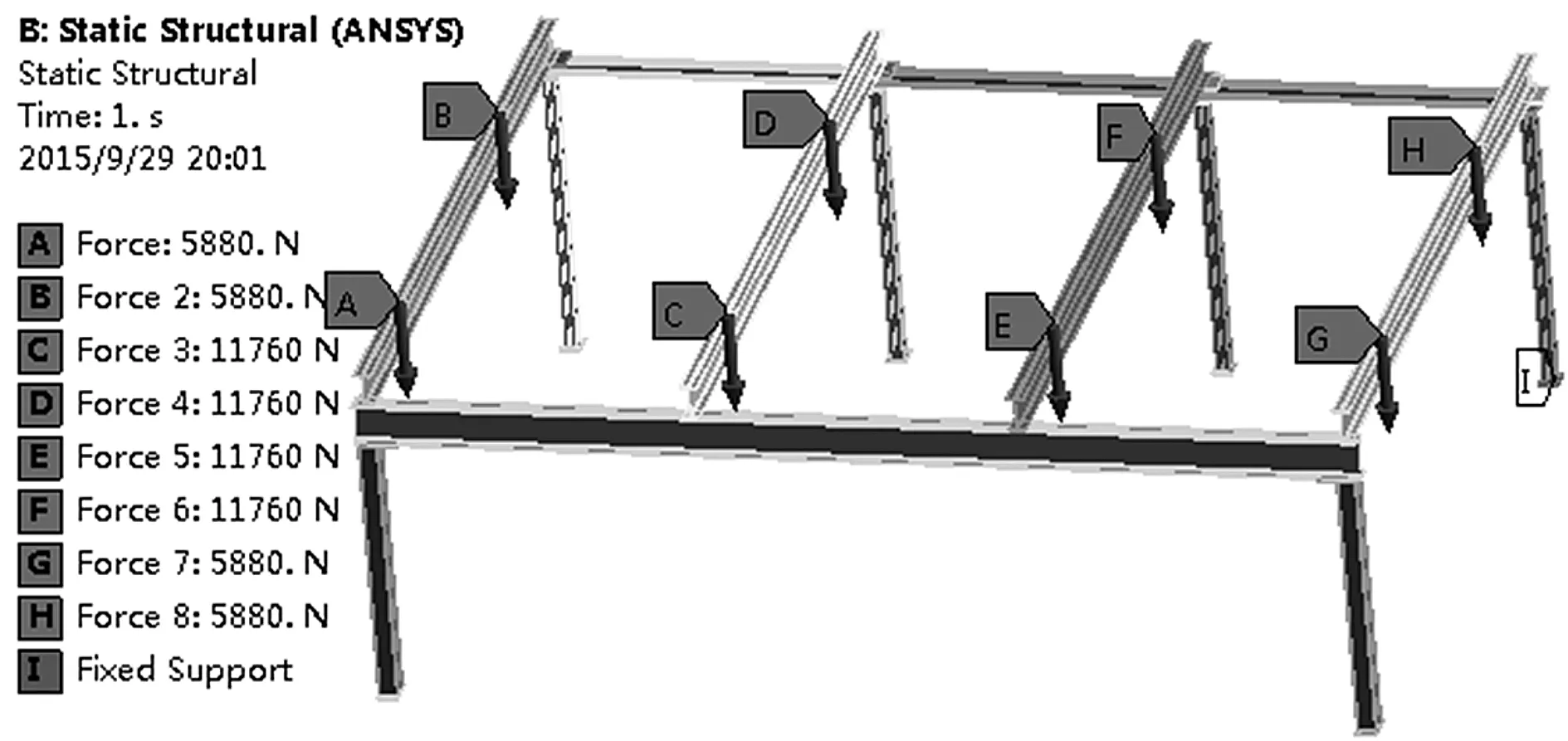
图3　立体车库的载荷与约束

2.4求解结果与分析

对立体车库进行有限元静力分析主要是对强度和刚度的求解，运用后处理模块Total Deformation和Equivalent Stress进行数据处理。求解后获得了该设备在满载工况作用下，整体应力大小及分布、局部应力集中和最大变形及位置等计算结果。

图4为ANSYS Workbench的计算结果，由图4可知：最大应力为153.07 MPa，发生在前立柱与前横梁连接处出现的明显应力集中，其他构件最大应力出现在中间两根纵梁上施加载荷处，分别为63.574 MPa和64.029 MPa；最大变形量为10.453 mm，出现在施加载荷最大的中间两根纵梁上。立体车库使用的材料主要是Q235，许用安全系数取1.3，许用应力[σ]=σs/[S]=235/1.3=181 MPa>153.07 MPa。所以该立体车库的强度足够，且有一定的裕量。再参考我国起重机相关标准校核变形，以及该厂家所要求的变形比率1∶500，则纵梁长度为5802 mm，许用挠度为：[y]=L/500=5802/500=11.604 mm>10.453 mm，因此刚度满足要求。链条式二层升降横移立体车库的钢架结构的有限元静力分析，证明了其刚度和强度满足安全使用要求，静力分析将作为立体车库下一步结构优化的基础。

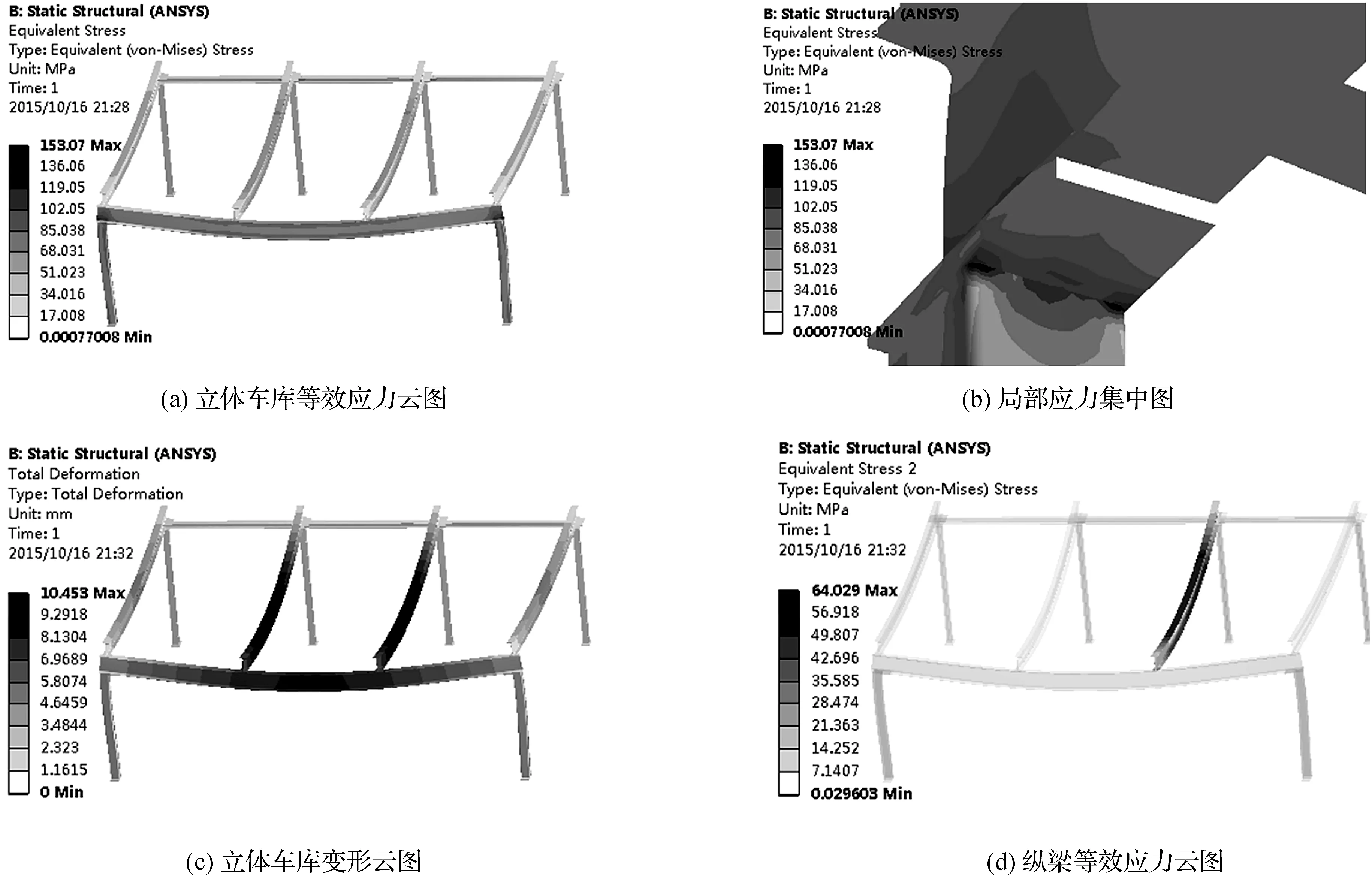
图4　有限元静力分析结果

3　经济型立体车库优化设计

优化设计是一种寻找确定最优设计方案的技术[19]，本文在立体车库的钢架结构有限元静力分析的基础上，利用ANSYS Workbench中优化设计模块Design Xplorer对立体车库进行结构优化。

3.1响应曲面分析

Design Xplorer 中的响应曲面分析法通过图表形式描述输入参数与输出参数间的关系，可直观观察各个输入参数影响的程度大小[20]。

3.1.1设置参数

由静力分析结果可以看出，中间纵梁在立体车库安全工作中举足轻重。由于车库结构的对称性，各纵梁间参数性能差别很小，优化立体车库只针对其中一根中间纵梁进行优化，优化中设置了一个输入参数即设计变量为中间纵梁截面宽度DS-Z23D1(如图 5所示)，由p1表示，优化前初始宽度为125 mm。设置了两个输出参数为中间纵梁最大等效应力和最大变形量，分别由p2、p3表示，初始值分别为64.029 MPa和10.453 mm。参数设置如表1所示。

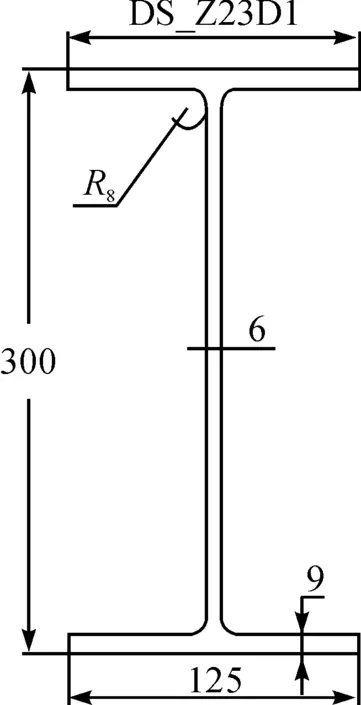
图　5纵梁截面CAD图(单位：mm)

参数属性参数名称初始数值单位输入参数纵梁截面宽度p1125mm输出参数纵梁最大等效应力p264.029MPa输出参数纵梁最大变形量p310.453mm

3.1.2响应曲面分析

根据系统提示对输入参数的范围进行设置，最小值与最大值范围为115～135mm，并更新设计点得到Design of Experiments(实验设计法，简称DOE法)的值，如表 2所示。

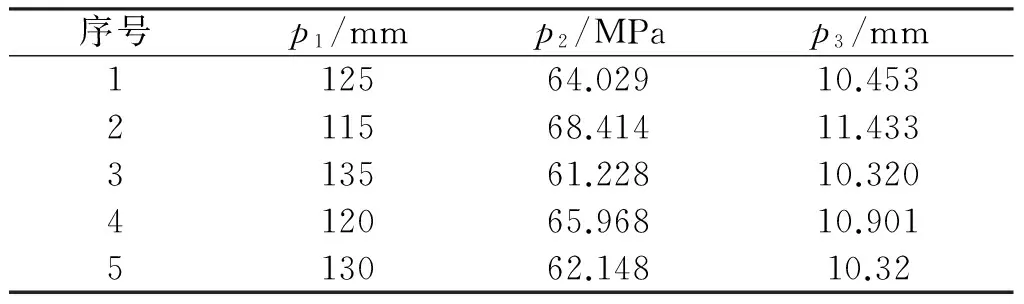
表2　DOE的值

计算得到参数间响应图以及响应灵敏度图，如图 6—图 8所示，响应图中每个点都对应一个设计点和一个响应参数值。

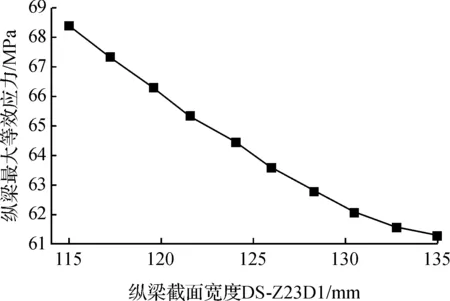
图6　纵梁截面宽度与最大等效应力响应图

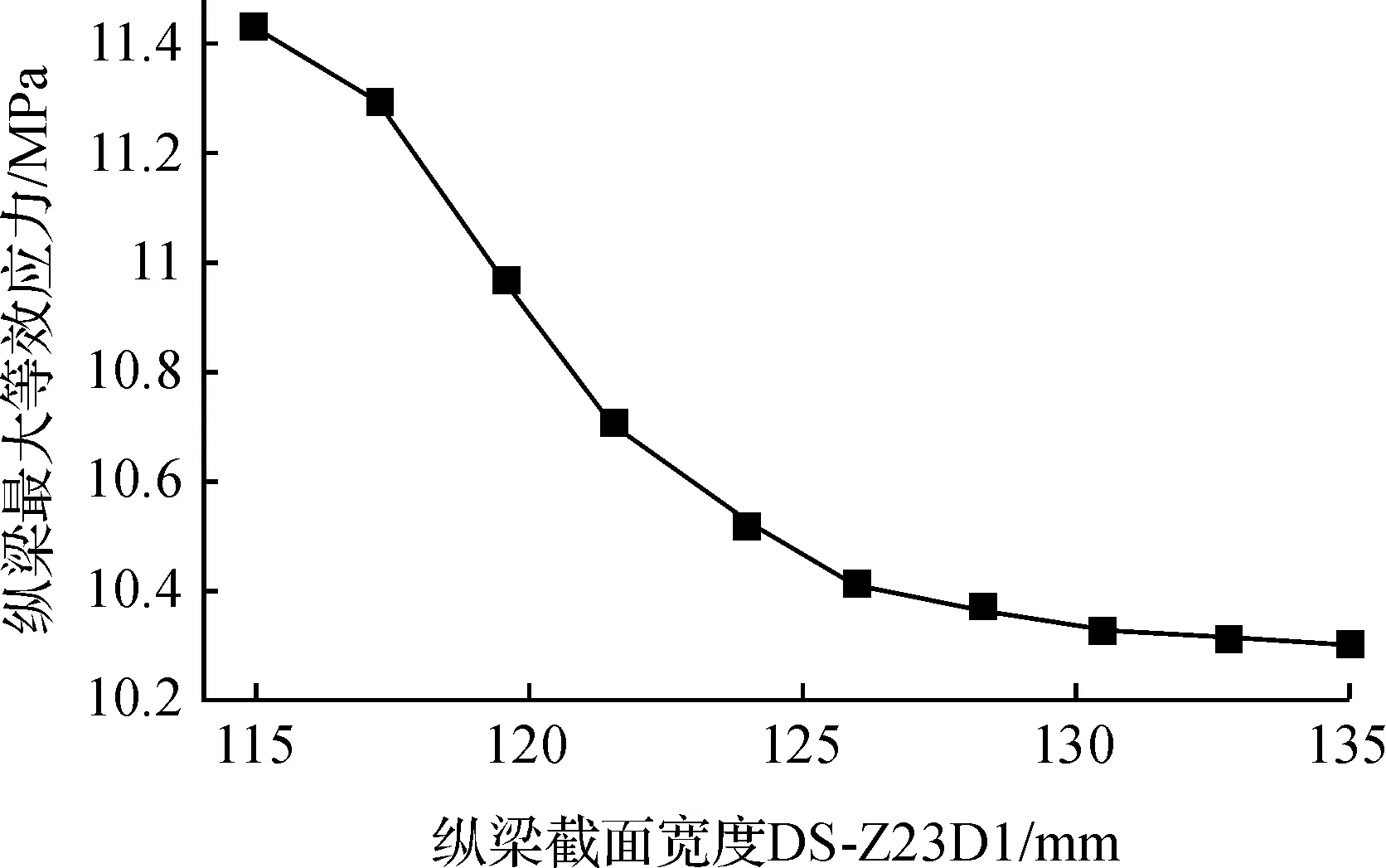
图7　纵梁截面宽度与最大变形响应图

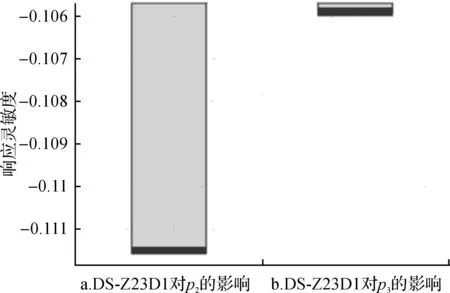
图8　纵梁截面宽度p1对最大等效应力p2和最大变形p3的响应灵敏度

由响应曲面分析结果可知，中间纵梁截面宽度p1与其最大等效应力p2呈现反比关系，宽度增加则应力减小，宽度减小则应力增加，响应图近似为一条斜率为负的直线。纵梁截面宽度p1与最大变形p3的响应图为一条曲线，当p1为115～125 mm间时，曲线斜率绝对值较大，宽度减小变形增大明显，当p1大于125 mm后曲线趋于平缓，最后趋向水平。由此可见，当纵梁截面宽度尺寸在敏感尺寸范围内变化对其最大变形影响明显，当尺寸大于某一值后，尺寸增大对刚度提高影响不再明显。从图 8灵敏度上更能清晰地观察到纵梁截面宽度p1与中间纵梁最大等效应力p2负相关程度较高。由于最大变形p3在数值上不如最大等效应力p2变化范围那么大，所以灵敏度值相对较小，p1与p3负相关度程度相对不高。

3.2立体车库零件优化

由优化结果可知，中间纵梁截面宽度为最小值115 mm时，其最大应力为68.414 MPa，小于许用应力，最大变形为11.433 mm，也在许用安全使用范围内。根据以上分析，优化方案采取四根纵梁截面宽度都设为115 mm具有可行性。优化零件，修改模型，重新进行静力分析得到计算结果[21]，并与立体车库优化设计前分析结果进行逐一对比，如表 3所示。

表3　优化前后参数对比

注：最大应力——车库整体最大应力、最大变形——车库整体最大变形。

由表 3可得，优化后即四根纵梁截面宽度减小为115 mm，纵梁上最大应力和最大变形分别为：67.454 MPa和10.912 mm，都有少量增加。立体车库整体的最大应力和最大变形分别为：152.81 MPa和10.912 mm，与优化前相比增加不明显，且都在安全许用值内，即立体车库优化后强度和刚度满足安全使用要求。对比优化前后立体车库的质量参数，立体车库整体质量由1418.9kg减少为1386.1kg，减少的质量是优化前的2.31%，用钢量明显减少。由此可见，此优化方案具有实际意义。

4　语　结

a)在SolidWorks中构建立体车库钢架结构模型，导入ANSYS Workbench建立有限元模型，然后对有限元模型进行静力分析。立体车库有限元静力分析中得到结构最大应力为153.07MPa，发生在前立柱与前横梁连接处，纵梁处存在较大应力为64.029MPa，结构最大变形为10.453mm，发生在施加载荷最大的两根中间纵梁上。分析结果验证了该立体停车库满足安全性强度和刚度要求。

b)利用响应曲面分析对立体车库零件进行优化设计，优化后，纵梁截面宽度减少为115mm，钢材使用量减少了2.31%，实现了立体车库结构的轻量化优化设计。

c)研究以立体车库钢架结构的有限元静力分析为基础。文中对立体车库强度和刚度的校核，以及结构的优化分析设计，是立体车库研究中一个完整的分析优化路线，为立体车库以及类似钢架结构设备的分析与优化提供了参考。

[1] KWAK H G, SONG J Y. Live load factors for parking garage members[J]. Structural Safety, 2000,22(3): 251-279.

[2] KWAK H G, SONG J Y. Live load design moments for parking garage slabs considering support deflection effect[J]. Computers and Structures, 2001,79(19): 1735-1751.

[3] 田广范,刘元洪,吴绪钧.日本国立体停车场的现状及我国发展立体停车场的动向与对策[J].建筑机械,1996,2(10):31-36,2.

[4] 胡清明.立体车库的结构优化与智能控制[D].广州:华南理工大学,2010:9-10.

[5] 刘良刚,喻钢.国内外电梯式立体停车库产品概况[J].停车场设备技术,1997,5(23):23-26.

[6] 方超林.立体车库发展的现状与挑战[J].中国高新技术企业,2013(9):160-161.

[7] 尤海珍,富阳.机械式停车设备失效模式研究及针对性检验方法[J].中国特种设备安全,2014,30(11):35-37,43.

[8] 徐格宁,王建民,高梅香.高层停车系统现代设计分析方法研究[J].太原重型机械学院学报,2001,22(1):1-4.

[9] 徐格宁,王建民,高有山,等.立体车库钢结构失效模式分析简化模拟及失效准则[J].中国机械工程,2002,13(19):1656-1657.

[10] 徐格宁,高梅香,王建民.高层停车库钢结构CAD/CAE软件系统集成研究[J].机械工程学报,2002,38(5):130-132.

[11] 荆友录,国兴玉.立体车库钢结构骨架的受力分析与结构优化[J].山东交通学院学报,2004,12(3):1-4.

[12] 李海英,宋华,付丽华.小容量经济型立体车库钢架结构的研究[J].鞍山科技大学学报,2007,30(5):485-488.

[13] 谭忠宏.电梯升降式立体停车库钢结构骨架的结构分析[J].科技资讯,2009(17):119-120.

[14] 贺玲芳.液压升降横移式全自动立体车库运动控制系统[J].机械科学与技术,2001,20(4):7-8.

[15] 钱惠君,徐卫国.升降横移停车设备的选型[J].中国电梯,2004(23):53-56.

[16] 刘金萍.龙门吊结构有限元分析[J].山西电子技术,2014,29(6):18-19.

[17] 万欣欣,王娟.单立柱巷道堆垛机满载下的静力分析[J].新技术新工艺,2014(12):51-53.

[18] 刘鑫,张祥林,冯科.基于ANSYS Workbench的冲压机械手机座优化设计[J].机械制造与自动化,2014,43(6):197-200.

[19] 李兵,何正嘉,陈雪峰. ANSYS Workbench设计、仿真与优化[M].北京:清华大学出版社,2013:158.

[20] 吴斌,钱晓明,武星,等.自动导引车骨架结构优化设计[J].中国机械工程,2014,25(19):2653-2657.

[21] 邓祖平,谷玉川,陈晶艳.基于有限元分析的轻卡车架优化设计及其台架试验[J].客车技术与研究,2014,36(2):54-57.

(责任编辑： 康锋)

Static Analysis and Optimization of Structure of Economical Stereo Garage

JIAOYingying,DUXiaoqiang,YUANBo,LINLepeng

(Faculty of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Since accidents frequently occur in stereo garage due to low structural strength, so a economical stereo garage manufactured by a company was taken as an example and a static analysis and optimization of its structure were carried out by using the CAD/CAE technology. First, the three-dimensional model of the stereo garage’s steel frame was set up in SolidWorks. Then, the finite element model established in ANSYS Workbench was leaded in it to make a finit element analysis on the steel-frame structure of stereo garage. Finally，an optimization of the parts of the stereo garage was completed based on the result of response surface analysis on its weak parts. The distribution laws of overall stress and deformation of the stereo garage during working hours were obtained; its maximum stress is 153.07 MPa and maximum deformation is 10.453 mm, so it meets the requirement of safe use. After the optimization design, 2.31% of steel consumption is saved while both the strength and stiffness of garage are guaranteed. The research provides a reference basis for the improvement of stereo garage.

stereo garage; finite element; static analysis; optimization design

10.3969/j.issn.1673-3851.2016.05.010

2015-09-09

浙江理工大学科研创新团队专项(13020049-Y)；浙江理工大学521中青年拔类人才专项

焦颖颖(1988-),女，山东菏泽人，硕士研究生，主要从事机械设计方面的研究。

杜小强, E-mail：xqiangdu@zstu.edu.cn

TH12

A

1673- 3851 (2016) 03- 0379- 06 引用页码： 050402