求解第一类Fredholm积分方程的修正CD共轭梯度法

王华军，赵汝文，朱志斌

(桂林电子科技大学 数学与计算科学学院，广西 桂林　541004)



求解第一类Fredholm积分方程的修正CD共轭梯度法

王华军，赵汝文，朱志斌

(桂林电子科技大学 数学与计算科学学院，广西 桂林541004)

为了求解第一类Fredholm积分方程，提出了一种修正的CD共轭梯度法，该算法在CD共轭梯度法上增加了一个梯度参数，并证明了该算法的全局收敛性。数值实验表明，与奇异值分解法相比，修正的CD共轭梯度法更有效。

第一类Fredholm积分方程；修正CD共轭梯度法；奇异值分解法

在天线设计、天体测定、图像复原、计算机X射线断层扫描等领域，第一类Fredholm积分方程扮演着重要的角色，但它是不适定的问题，不存在唯一解。

第一类Fredholm积分方程的一般形式[1]为：

(1)

其中：x′为已知点；g(x)为x的观测值；A(x-x′)为高斯核函数；f(x′)为x′的真实值。选取一维高斯核函数：

(2)

其中，参数c、γ均为正数。

求解方程(1)的方法有小波多元函数逼近法、快速多尺度算法、奇异值分解法、最小二乘法，但这些方法求解效果不理想，为此，提出一种修正CD共轭梯度法。

1　修正CD共轭梯度法

修正CD共轭梯度法的迭代形式为：

(3)

其中：xk为x的第k次迭代；αk为强Wolfe搜索产生的步长；dk为搜索方向，且

(4)

gk为xk的梯度，βk为方向调控参数。其中著名的βk计算公式有[2-3]

(5)

(6)

(7)

2　 算法及其收敛性

2.1修正CD共轭梯度法

1)选取参数0<δ<0.5<σ<1，d1=-g1，x1∈Rn，k=1，ε≥0。若‖gk‖≤ε，算法停止。

2)由强Wolfe线搜索准则计算步长αk，即αk满足：

(8)

(9)

3)由式(3)计算xk+1，若‖gk+1‖≤ε，算法停止。

4)由式(4)计算dk+1。

5)k∶=k+1，转步骤2)。

假设‖gk‖≠0，否则算法找到稳定点而停止。

引理1设{gk,dk}为修正CD共轭梯度法生成的序列，则

(10)

证明设θk为向量gk+1与gk的夹角，则

(11)

(12)

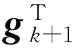
引理2若步长αk满足式(8)、(9)，则

(13)

证明设θk为向量gk+1与gk的夹角，则

即引理2得证。

2.2算法的全局收敛性

为了证明修正CD共轭梯度法的全局收敛性，假设：

1)目标函数f(x)在其水平集Ω={x∈Rn|f(x)≤f(x1)}上有界。

2)f(x)的梯度g(x)在Ω上Lipschitz连续，即存在L>0，使

引理3假设1)、2)成立，{gk,dk}为修正CD共轭梯度法生成的序列[6]，则

(14)

证 明若定理1不成立，则存在常数r>0，使得任意k≥1，有‖gk‖≥r。由式(4)得dk+gk=βkdk-1，两边取模平方移项，并利用式(13)得

利用d1=-g1，

结合‖gk‖≥r，

对上式两边分别求和，

与式(14)矛盾，所以定理1成立。

3　数值实验

为了验证修正CD共轭梯度法的有效性，进行了数值实验并与奇异值分解法对比。实验函数为第一类Fredholm积分方程[1]。算法测试的环境为Matlab2013a，Windows7操作系统，IntelCorei3-2370MCPU2.40GHz。选取参数δ=0.025，σ=0.9。奇异值分解法和修正CD共轭梯度法的数值结果如图1、2所示。2种方法的运行时间和平均误差见表1。从表1和图1、2可看出，修正CD共轭梯度法比奇异值分解法更有效。

图1　奇异值分解法的数值结果Fig.1　Numerical results of singular value decomposition method

图2　修正的CD共轭梯度法的数值结果Fig.2　Numerical results of the modified CD conjugate gradient method

方法运行时间/s平均误差奇异值分解法11.0102930.0135修正CD共轭梯度法0.0124100.0072

4　结束语

为求解第一类Fredholm积分方程，提出了一种修正的CD共轭梯度法，并证明了该方法的全局收敛性。与奇异值分解法[9]相比，修正的CD共轭梯度法更有效。

[1]VogelCR.ComputationalMethodsforInverseProblems[M].北京:清华大学出版社，2011:1-11.

[2]DAIYuhong,YUANYaxiang.Anonlinearconjugategradientmethodwithastrongglobalconvergenceproperty[J].SIAMJournalonOptimization,1999,9(8):177-182.

[3]StoreyC.Efficientgeneralizedconjugategradientalgorithms[J].JournalofOptimizationTheoryandApplication,1991,24(6):129-137.

[4]董晓亮,谢星星,侯志军,等.3种推广的DY共轭梯度法及其全局收敛性[J].广西科学，2010,17(4):321-323．

[5]卿倩,胡娟娟,王硕.广义Wolfe线搜索下共轭梯度法的全局收敛性[J].桂林电子科技大学学报,2011,31(4):342-344.

[6]江羡珍,马国栋,简金宝.Wolfe线搜索下一个新的全局收敛共轭梯度法[J].工程数学学报,2011,28(6):779-786．

[7]张小让,朱志斌,邢明燕.一种修正下降的非线性共轭度法[J].桂林电子科技大学学报,2015,35(5):424-426.

[8]黄海.非线性无约束优化问题的新共轭梯度法[J].河南大学学报,2014,3(2):142-145.

[9]高阳,肖立志.用改进截断奇异值分解法反演核磁共振弛豫时间[J].石油地球物理勘探,2015,12(2):376-381.

编辑：曹寿平

A modified CD conjugate gradient method for solving Fredholm integral equation of the first kind

WANG Huajun, ZHAO Ruwen, ZHU Zhibin

(School of Mathematics and Computational Science,Guilin University of Electronic Technology, Guilin 541004, China)

In order to solve Fredholm integral equation of the first kind, a modified CD conjugate gradient method is proposed. A gradient parameter is added in CD conjugate gradient method, and the global convergence of the algorithm is proved. Numerical experiments show that compared with singular value decomposition method, the modified CD conjugate gradient method is more effective.

Fredholm integral equation of the first kind; modified CD conjugate gradient method; singular value decomposition method

2015-11-10

国家自然科学基金(11361018)；广西自然科学基金(2014GXNSFFA118001)；桂林市科学研究与技术开发计划(20140127-2)；广西教育厅科研项目(KY2016YB167)；桂林电子科技大学研究生教育创新计划(2016YJCX46)

朱志斌(1974-)，男，湖南双峰人，教授，博士，研究方向为最优化方法及其应用。E-mail:zhuzb@guet.edu.cn

O224

A

1673-808X(2016)04-0342-03

引文格式：王华军，赵汝文，朱志斌.求解第一类Fredholm积分方程的修正CD共轭梯度法[J].桂林电子科技大学学报，2016,36(4):342-344.