基于费效分析的舰船备件优化模型研究

刘海，程科，高尚

（江苏科技大学 计算机科学与工程学院，江苏 镇江　212003）

基于费效分析的舰船备件优化模型研究

刘海，程科，高尚

（江苏科技大学 计算机科学与工程学院，江苏 镇江212003）

舰船备件优化是保证舰船系统各装备高任务可靠性的一个重要手段。为了权衡备件供应保障中的经费与备件需求的矛盾，针对不可修复系统，建立了定可靠度备件优化和定费用备件优化的两个模型，并对启发式算法中的搜索方向函数进行了改进和化简，给出了解此两个优化模型的启发式算法。结合上述两个优化模型和费效分析准则，提出了费效分析备件优化模型，并给出了有效算法。结合舰船备件的案例，验证了方法的有效性及实用性。此模型可为舰船装备保障人员制定保障方案提供辅助决策。此模型具有较好的可扩展性，修改此模型可解决可修复系统的备件优化问题。

库存；优化；费效分析；备件；不可修复备件

舰船执行任务的环境主要是远离陆地的水面，尤其是远洋海面运输和战斗任务，因此舰船装备性能完全取决于装备自身质量和有效的装备后勤管理工作。有效的装备后勤管理工作主要是指装备的保养和维修以及备件的管理，其中备件管理随着舰船现代化技术的发展其地位越来越重要。

舰船备件管理的核心内容之一就是受损装备部件的维修更换和备件库存的优化管理，受损装备部件的维修更换是指一旦舰船某装备受损应立即有相应备件替换，同时根据装备部件自身的特性决定是否需要维修以重新使用。而备件库存的优化管理是指从经济上和装备性能可靠性上充分考虑备件的库存数量，既不能过多，又不能过少。因此科学合理地采用合适的备件优化模型，以供后勤管理人员实现备件的优化管理，是保证舰船装备各部件质量、性能和可靠性的关键研究内容［1-4］。

一直以来，关于备件优化模型及其在军事和民用领域的应用国内外学者进行了大量的研究［5-9］。文献［10］将备件分成可修复 （repairable parts）和不可修复备件 （non-repairable parts）两大类，常见的研究都是基于可修复备件［10-13］，通过修复可以重新投入使用，而不可修复备件是指一旦受损必须更换和丢弃。但不可修复备件也是后勤管理关键环节，需要做深入研究［10，14］。本文针对不可修复备件，分别研究了定可靠度和定费用优化模型，并对解决此问题的启发式算法进行了改进和优化。此外，考虑到费效分析是一种有效的平衡可靠度和费用的决策方法，基于我们前期的工作［15］，提出了基于费效分析的舰船备件优化算法。

1　备件优化模型

1.1基本概念

备件（Spare parts）是指在装备后勤管理工作中，事先准备的用于受损装备部件维修和更换而用的各类零部件库存。备件按是否可维修重复使用又分为以下两类［10］：可修复备件和不可修复备件。

可修复备件是指备件本身是可以修复的，或者是从经济上优先考虑修复的部件。在舰船执行任务时期，当一个装备受损时，应立即从库存中取出对应备件加以更换，同时受损备件通过后勤维护中心修复后重新进入库存，有时也称为备用备件或循环备件。

而不可修复备件则是从技术角度不能或难以修复的备件，也可能是从性价比上考虑不值得维修的消耗性零部件。一旦舰船装备部件受损，只需从库存中选用库存新备件即可，因此，有时也称为消耗备件（consumable parts）或丢弃备件。

1.2不可修复备件优化模型

近年来，针对可修复备件优化问题研究较多，而不可修备件更需要对库存数量进行充分考虑。如果将整个舰船系统看成一个整体，显然其中任何一种零部件受损都会导致系统出现故障，影响系统性能，因此这个系统就非常类似于各个零部件串联的电路系统。以下的分析正是基于这一假设而进行，同时为了模型的简洁有效，研究中不考虑不可修复备件的更换时间，也不考虑备件是否在库存过程中是否性能降低或失效。

模型的符号约定如下：

RS为舰船系统可靠度，Ri为舰船上装备的第i种零部件可靠度，R0为舰船系统预设可靠度；

CS为舰船系统所有装备零部件的库存备件总费用值，ci为系统中第i种零部件单价；C0为预定库存备件总经费；

n为舰船各种零部件的类别总数；

xi为第种零部件总数（包含库存备件和运行部件）；

T为舰船各部件执行任务的平均时间；

λi定义为第i种零部件的失效系数，令λi=aibi，其中ai为正在使用的第i种零部件数量；bi为其可能失效的几率，且假设元件寿命服从指数分布。

由可靠性理论可知，第i种舰船零部件的可靠度可由下式给出。

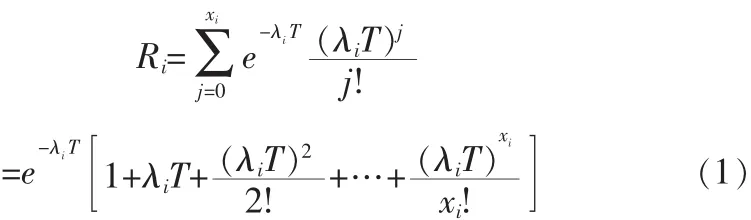
舰船稳定工作的系统可靠度RS可由公式（2）给出。

目前有两种主要模型：

1）定可靠度库存备件优化模型

该模型的思路是预先设定舰船系统工作可靠度，在满足该可靠度的前提下，以尽可能低的费用，合理配置库存各种备件的种类和数量，如公式（3）描述。

xi为正整数

公式（3）中minCS即为定可靠度模型求得的整个舰船所需库存备件的最小总费用。

2）定费用库存备件优化模型

该模型考虑如何在系统所能承受的费用前提下，整个系统工作的可靠度达到最大值，即在给定费用的情况下，合理配置库存备件的种类和数量，而使系统各部件运行更加可靠。

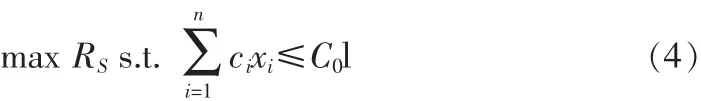
xi为正整数

公式（4）在保证系统所有库存备件的费用小于等于预定费用的前提下，获得系统运行的最高可靠度。

1.3简化的启发式搜索方向函数

分析前述定可靠度和定费用库存备件优化问题，可以看出其实质其实就是库存备件种类和数量的组合优化问题。组合优化问题的难点在于随着舰船系统中的备件数量和种类的增加，传统的处理方法会导致系统几何级数爆炸，因此常用启发式算法来解决。

启发式算法的核心是搜索方向函数，这里考虑采用采用逐步构造最优解的方法。思路是：整个系统的所有部件都是最优配置，即从第一种备件开始，每增加一种备件都重新计算可靠度，按可靠度最大来优化，直至系统所有种类的部件增加完毕，按公式（5）来描述。

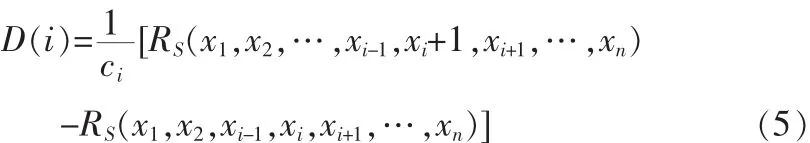
以定可靠度备件优化模型来说，如果公式（5）计算的结果是第i种部件的D（i）最大，而可靠度值还未达到预定可靠度，则下一步就将第i种部件的数量加一。反复循环，直到系统可靠度达到预定值，即RS≥R0为止。

由于搜索方向函数（5）式计算比较复杂，可采用如下公式

下面对搜索方向函数式（6）进行化简：

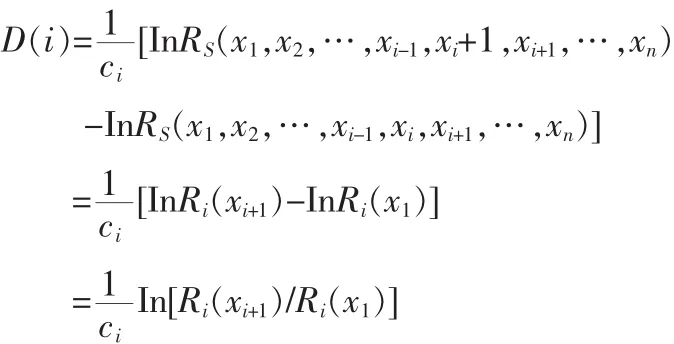
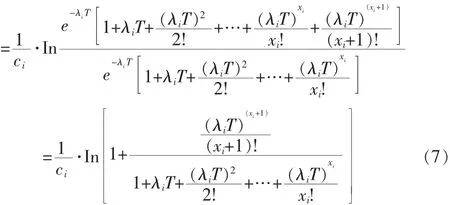
具体算法如下：

1）令（x1，x2，…，xn）=（1，1，…，1），计算系统的战备可靠度RS；

2）按公式（7）计算搜索方向函数；

3）如果其中最大者为D（i*），则将第i种部件加1个，即xi*=xi*+1，计算系统的战备可靠度RS；

4）RS是否大于或等于预定的可靠度R0，如满足条件，算法停止，否则转2）。

类似地，对于定费用备件优化模型来说，如果公式（5）计算的结果是第i种部件的D（i）最大，而费用尚未超过预定值C0，则下一步就将第i种部件的数量加一，反复循环。

具体算法如下：

1）令（x1，x2，…，xn）=（1，1，…，1），计算总经费

2）按公式（7）计算搜索方向函数；

3）如果其中最大者为D（i*），则将第i*种部件加1个，即xi*=xi*+1，计算总经费

4）总经费CS是否大于C0，如满足条件，算法停止，将第i*种部件刚加1个的取消，即xi*=xi*-1，否则转2）。

2　基于费效分析的备件优化模型

对于定可靠度备件优化模型和定费用备件优化模型中，预定的可靠度R0和给定经费C0一般由经验给出，没有科学依据，依据费效分析准则［14］，可以以可靠度和费用的比值作为目标函数，建立备件优化模型:

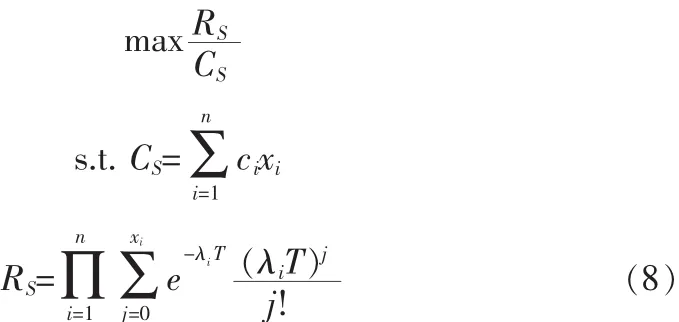
对于规划（8），得到的最有解（R*S，C*S），但 R*S有可能比较小，或者C*S有可能太大，出现这种情况结果不能令人满意。因此可以把可靠度或费用因素也考虑到模型中，模型如下，如只考虑可靠度，模型如下：

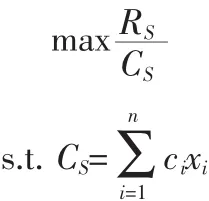
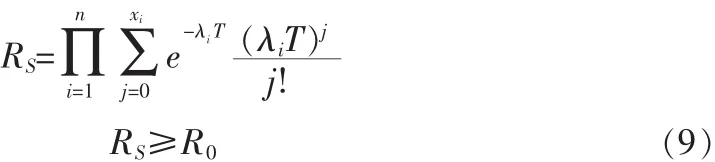
xi为正整数其解法如下：

1）令（x1，x2，…，xn）=（1，1，…，1），计算系统的战备可靠度RS；

2）按公式（7）计算搜索方向函数；

3）如果其中最大者为D（i*），则将第i*种部件加1个，即xi*=xi*+1，计算系统的战备可靠度RS和

4）如RS≥R0，转5），否则转2）；

如递减算法停止，反之转2）。

3　案例分析

假设某舰船的主要元件有20种，其参数如表1，装备执行任务平均时间T=2，利用规划（3），经过计算，当RS≥R0= 0.999 9时，结果如表1所示，每一步迭代的费用和可靠度如图1所示，此时：CS=657万，RS=0.999 933。

表1　某舰船的可靠性数据及备件Tab.1 The reliability of the data and spare parts of a ship

从图1可以看出，随着费用的增加，可靠度趋于饱和。可靠度费用比值与可靠度关系如图2所示，当可靠度RS=0.802 3时，可靠度与费用比值最大，但此时RS=0.802 3并不高，因此可以以可靠度和费用的比值作为目标函数，同时预定的可靠度，如R0=0.99，其模型如下：

xi为正整数

此时备件数分别为：2，2，2，3，2，4，4，4，3，2，2，1，2，3，2，3，3，4，2，2。CS=384万，RS=0.990 464。

图1　每次迭代过程中费用与可靠度关系Fig.1　The relationship between cost and reliability

图2　可靠度费用比值与可靠度关系Fig.2　The relationship between the ratio of reliability to cost and the reliability

4　结　论

备件优化是保证舰船整个系统中各装备高任务可靠性的一个重要手段。文章首先分析了定可靠度优化模型和定费用优化模型，并提出了一种简化的方向搜索函数用于优化模型的启发式求解，此外，基于费效分析方法，提出一种新的舰船备件优化模型，为舰船系统各装备备件的优化决策提供了一种有效的途径。对于可修复系统的备件优化可建立类似的优化模型。

［1］Barata J，Guedes Soares C，Marseguerra M，et al.Simulation modeling of repairable multi-component deteriorating systems for‘on condition'maintenance optimization.Reliability Engineering&System Safety，2002，76（3）:255-264.

［2］Marseguerra M，Zio E，Podofillini L.Multi-objective spare part allocation by means of genetic algorithms and Monte Carlo simulation.Reliability Engineering&System Safety，2005，87:325-335.

［3］刘喜春，郑华，仲辉.备件配置优化问题研究［J］.系统工程与电子技术，2008，30（10）：1934-1937.

［4］郭继周，郭波，张涛，等.地空导弹维修保障能力评估与备件优化模型［J］.火力与指挥控制，2008，33（3）：9-12.

［5］陈士涛，杨建军，张森.地空导弹装备备件资源优化配置模型研究［J］.战术导弹技术，2010，31（5）：62-66.

［6］王睿，李华，李庆民，等.基于舰艇编队任务可靠性的备件优化配置［J］.兵工自动化，2011，30（10）：1-4.

［7］ZHAO Jian-zhong，LI Hai-jun，YE Wen，et al.Optimization Configuration Modeling of Spare Parts under Constraint of Improved System Spare Part Fill Rate［J］.Acta Armamentarii，2013，34（9）:1187-1192.

［8］Adriaan Van Horenbeek，Liliane Pintelon，Philip A.Scarf，Cristiano A.V.Cavalcante.The Effect of Maintenance Q-uality on Spare Parts Inventory for a Fleet of Assets［J］.IEEE Tra-nsactions on Reliability，2013，62（3）:596-607.

［9］WANG Zheng-yuan，CAO Ji-ping，ZHU Yu，et al.An Optimization Model of Wartime Spare Parts Resource Allocation on Consideration of Maintainability［J］.Acta Armamentarii，2014，35（5）:719-724.

［10］Louit，D.，Pascual，R.，Banjevic，D.，et al.Optimization models for critical spare parts inventories-a reliability approach ［J］.Journal of the Operational Research Society，2011（62）: 992-1004.

［11］Mirzahosseinian，H.，Piplani，R.A study of repairable parts inventory system operating under performance-based contract ［J］.European Journal of Operational Research，2011，214（2）: 256-261.

［12］Sel uk B.An adaptive base stock policy for repairable item inventory control［J］.International Journal of Production Economics，2013，143（2）:304-315.

［13］Xue Tao，Feng Yun-wen，Qin Qiang.Optimization of Repairable Spare Parts for K/N Cold-Standby Redundant System Considering Scraps［J］.Journal of South China University of Technology（Natural Science Edition），2014，42（1）:41-46.

［14］Jakiul Hassan，Faisal Khan，Mainul Hasan.A Risk-based Approach to manage non-repairable Spare Parts Inventory［J］. Journal of Quality in Maintenance Engineering，2012，18（3）: 344-362.

［15］高尚.费用效能分析的准则探讨［J］.上海航天，1995，12 （3）：18-1220.

Optimization models based on cost effectiveness analysis for naval ship spare parts

LIU Hai，CHENG Ke，GAO Shang
（School of Computer Science and Engineering，Jiangsu University of Science and Technology，Zhenjiang 212003，China）

Spare parts optimization plays an important role in ensuring high mission reliability of the naval ship's weapons and equipment systems.In order to balance contradiction between maximization of reliability and minimization of costs in the spare parts supply，two spare parts optimization models with constant reliability and constant cost for the non-repairable system were considered respectively.To solve the two optimization models，heuristic algorithms with improved and simplified search function are given.After that，on the basis of cost effectiveness analysis method，the ratio of reliability and cost was set to be objective function to build a new spare parts optimization model，and then its corresponding algorithm was produced.Finally，the proposed method was proved to be effective and practicable by numerical example.This new model can help equipment support personnel making decision，and due to its good scalability，it can be extended to solve repairable spares problem.

inventory；optimization；cost-effectiveness analysis；spare parts；non-repairable parts

TN-8

A

1674－6236（2016）05-0001-04

2015-11-03稿件编号：201511030

国家自然科学基金资助项目（61471182）；江苏省科技创新与成果转化（重大科技成果转化）项目（BA2012129）；江苏省研究生科研创新计划项目（1252209AK）；江苏大学现代农业装备与技术省部共建教育部重点实验室开放基金资助项目（NZ201303）

刘 海（1991—），男，安徽东至人，硕士研究生。研究方向：模式识别。