强力旋压连杆衬套本构关系研究

山西中北大学机械与动力工程学院　吕创能　樊文欣

强力旋压连杆衬套本构关系研究

山西中北大学机械与动力工程学院吕创能樊文欣

利用正交试验的方法，通过对不同的旋压参数下试件的准静态拉伸试验，得各个试件弹性阶段的弹性模量E、泊松比λ、以及力—位移曲线。通过对各个应力应变曲线的分析，得到各个试件主要力学性能参数。选取适合QSn7-0.2的应力—应变关系模型，即Ramberg-Osgood模型，研究强力旋压工艺参数对旋压试件本构关系参数的影响，得出了模型参数关于成形工艺参数的三元二次回归方程，并对方程进行了误差检验，结果是理论曲线与实测曲线十分接近。

强力旋压，本构关系，应力—应变关系

1　引言

连杆衬套是连接柴油机活塞销与连杆小头的轴承部件，在工作中承受高温、高压作用，工作条件恶劣。本构关系是材料的固有属性，它反映了应变与应力之间的关系，通常用本构关系模型来表述［1］。本构关系模型建立的过程，就是将材料的变形规律通过数学公式表示出来并通过计算预测出材料的变形行为的过程。

2　试验

2.1强力旋压试验

将QSn7-0.2棒料车削制成内径为42mm，外径为55mm，高为90mm的筒形件15件。本次试验选取减薄率、进给比和去应力退火温度三个因素，每个因素选取五个值，将这三因素五水平试验全部组合，采用正交试验的方法，需要做15次试验，然后对15件样件进行旋压、热处理加工。

2.2拉伸试验

通过室温下静态拉伸试验与准静态拉伸试验，分别得到不同强力旋压工艺参数下各个试件弹性阶段的弹性模量E、泊松比λ、以及力—位移曲线［2］。在静态拉伸试验中，使用电测法测出试件弹性变形时的弹性模量E和泊松比λ。通过测量计算出的E、Rp0.2、εm、Rm如表1所示。

3　本构方程的确定

本文的本构关系模型选取与QSn7-0.2应力—应变曲线相符合的Ramberg-Osgood应力—应变关系模型。

3.1变参数Ramberg-Osgood应力—应变关系模型

通过Ramberg-Osgood模型拟合旋压前后试件的应力—应变关系时，发现应力范围在Rp0.2与Rm之间的部分不吻合，拟合的数据比试验所得数据整体偏高，因此，将应力—应变曲线分为弹性变形阶段和塑性变形阶段两部分，分别使用Ramberg-Osgood模型进行拟合［3］。

3.1.1弹性变形阶段

由Ramberg-Osgood模型可知：

弹性模量仍取值E=130.53Gp，对于Rp的选择有两种，在这里采用比较经典的假设，即规定塑性延伸率为0.2%时的强度Rp0.2。当应力小于Rp0.2时，QSn7-0.2的本构模型可采用标准的

表1　试件力学性能

Ramberg-Osgood模型，即上式可转化为：

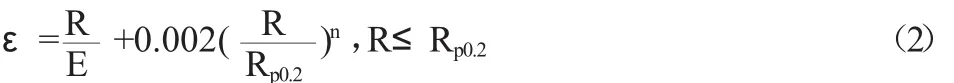
其中，Rp0.01为规定塑性延伸率为0.01%时的强度，也就是通常所说的比例极限。通过图解法与计算法确定Rp0.01为规定塑性延伸率和硬化指数n，然后由回归正交表拟合出n的回归方程：

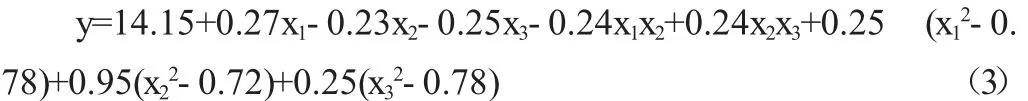
经过显著性检验，所有偏回归系数都不显著。回归方程简化为常函数：

根据回归方程方差分析，在本次试验旋压工艺参数取值范围内，各个因素对硬化指数的影响都不明显，对其取整后可得硬化指数n=14，与旋压前硬化指数相比没有变化。

3.1.2塑性变形阶段

由QSn7-0.2应力—应变曲线可知，应力大于Rp0.2小于Rm时的曲线和应力小于Rp0.2时的曲线形状相似，所以应力大于Rp0.2小于Rm范围内的曲线也可以用Ramberg-Osgood模型表示，当应力大于Rp0.2时，将Ramberg-Osgood表达式从原点移动到Rp0.2处，如式：

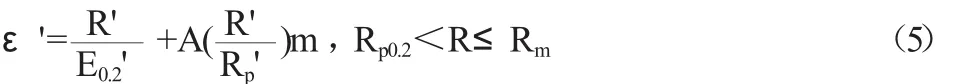
其中，ε'和R'分别为线性转化后的应变与应力，Rp'为转化后的参考应力，m是通过应力为Rp0.2和Rm之间的一个点确定的形状指数，当m=1与m＞1模型的曲线与QSn7-0.2的应力—应变曲线相符。

抗拉强度Rm为最大力时对应的强度，由回归正交表得出Rm回归方程：

通过计算，可得塑性阶段Ramberg-Osgood模型参数，由回归正交表得出回归E0.2'方程：

经过显著性检验，该方程所有偏回归系数都不显著，则回归方程可简化为常函数：

根据回归方程方差分析，在本次试验旋压工艺参数取值范围内，各个因素对处切线模量的影响都不明显，因此，模型中切线模量E0.2'=18.28Gpa。同理，由回归正交表得出硬化指数m=4。

3.2Ramberg-Osgood模型的误差检验

对比部分试件的试验应力—应变曲线与理论曲线，可看出各个试件的理论曲线与实测曲线十分接近，在曲线拐弯处略有差别。在Ramberg-Osgood模型中，弹性模量E，规定塑性延伸强度Rp0.2及其切线模量E0.2'，硬化指数n、m，抗拉强度Rm及其应变值εm，这几个重要的参数三元二次方程的准确度决定了模型的准确度，实验值与理论值的偏差：E的最大偏差为1.86%、Rp0.2的最大偏差为2.01%、Rm的最大偏差为1.58%，这些参数的偏差都很小，但εm的最大偏差达到了10.63%。基于Ramberg-Osgood模型的旋压试件应力—应变模型的可描述为：

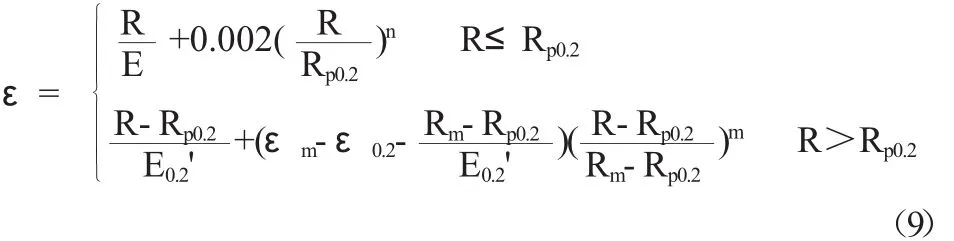
其中，

4　结论

（1）利用正交方法，设计连杆衬套强力旋压，然后对试件进行静态拉伸试验，记录其力—位移曲线，通过计算得出应力—应变曲线，通过测量计算得出弹性模量E、规定塑性延伸强度Rp0.2、抗拉强度Rm及其应变值εm，为构建本构关系方程提供了试验数据。

（2）Ramberg-Osgood模型可以很好地描述强力旋压成形后试件的应力—应变关系，各个本构关系参数可以通过三元二次回归方程表示。通过比较本构关系模型与试验所得的应力—应变曲线，对模型进行了误差分析，表明该模型能够很好地描述不同强力旋压成形工艺参数下的应力—应变关系。

［1］彭大暑.塑性成型原理［M］.长沙：中南大学出版社，2004，2-45.

［2］GB/T228-2010.金属材料室温拉伸试验方法［S］.

［3］李涛，樊文欣，周永召等.筒形件强力旋压成形本构关系研究［J］.热加工工艺，2014，43（5）：104-106.

吕创能，1989年出生，湖北武汉人，硕士研究生，研究方向：机械振动与噪声控制、连杆衬套强力旋压。