人体下肢康复机构的研究与分析

2016-09-13山西中北大学机械与动力工程学院李小龙梅瑛申登高

河北农机 2016年2期

山西中北大学机械与动力工程学院　李小龙　梅瑛　申登高

人体下肢康复机构的研究与分析

山西中北大学机械与动力工程学院李小龙梅瑛申登高

本文以剖析人体下肢解剖学理论为依据，设计了一种基于混联机构原理的新型下肢髋、膝、踝关节运动矫正机构。该机构按照正常人体下肢基本尺寸范围，对下肢运动矫正机构的结构进行了数学建模并进行了运动学仿真分析，验证了该并联机构可以有效辅助运动功能障碍者恢复健康，并应用Pro/E强大的三维建模功能进行建模。该机构结构简单、工作空间较大、刚度大，适用于不同群体。

康复机构；位置逆解；椭圆形轨迹；混合驱动

引言

为了减轻护理员对下肢患者的护理强度，使患者能及时地得到辅助关节治疗，研究康复训练机构意义重大。护理人员的护理肯定是复杂的，但护理费用比较昂贵［1］。器械护理不可能达到护理员对患者的护理效果，器械只能够达到几种重要的运动，可以实现患者的康复要求。能达到目的，这种方法就是可行的，所以本文设计了一种新型髋、膝、踝关节康复机构，该机构可以实现人体正常行走的轨迹要求。

1　髋、膝、踝关节运动矫正机构的设计及运动学分析

平面及空间机构的位置逆解是工作空间、奇异位形、传递性能、动力学等方面的研究前提［2］，因此位置逆解问题是平面和空间机构运动学研究中最为重要最为基础的问题，所以本文重点研究位置逆解。在位置逆解分析中，采用闭环几何法与复数矢量方程法［3］相结合的方法对其位置逆解进行求解，建立机构的闭环方程并根据机构的特点建立约束方程进行正、逆解求解，最终得到机构的位置逆解解析表达式。

1.1机构位置逆解数学建模

1.1.1位置分析

图1为混合驱动康复机构原理图，建立如图所示的直角坐标系。图1将康复机构分成4个矢量环：AEGF、EGD、GDC、CHB。知该机构的结构参数为L1、L2、L3、L4、L5、L6、L7、φ1、φ7、α1、r1、r6、r7，杆ED对应的方向角为0，H=E—→D+h。

图1　下肢康复机构原理

固定铰链A、B、E的坐标分别为（XA、YA）、（XB、YB）、（0、0）。机构的逆运动学分析是已知系统的几何关系、输出端C点的运动参数，求解常速电机、伺服电机的运动参数。如图1所示，选出合适的矢量闭环，进行数学建模。求曲柄AF、BH的角位移φ1、φ7

如图1所示，在建立矢量环AEGF、GDC、CHB、BHCDGE中建立矢量方程：

以复数形式表示并按欧拉公式展开得：

令上述方程的实部和虚部分别相等，并带入已知条件L2、L3L4、L5、L6、φ2、φ3、φ4、φ5、φ6，C点坐标（XC、YC），可解得，

2　Pro/E三维建模及下肢康复机构输出轨迹

根据人体步态分析可知，一只脚在行走过程中，其摆动一个周期所形成的轨迹近似为卵形形状（类椭圆），而人正常行走两腿的相位差是180°。因而人在正常行走过程中，脚心的步行轨迹是近似鹅卵形，卵形（类椭圆）的长轴为步长，短轴为脚离地的高度［4］。因而根据正常步态的基本参数可知，正常人步长为50～80cm，步高约为5cm。因而在设计中可以认为长轴长为50～80cm，短轴长为步高的两倍，即10cm，考虑到不同步态患者的步高也是不同的，因此短轴的长度选取为8～12cm。考虑到本康复医疗器械主要针对腿部负伤康复期患者，由于是非正常人体，所以步幅和步长做一些相应的调整。适当考虑减少步长选取为40～50cm，患者步高为4～6cm。根据以上分析，设计出可以模拟适合椭圆轨迹或者近似于椭圆轨迹的机构，如图2所示。根据以上参数经计算初选杆长如表1所示（省略详细计算过程）。

表1　各杆长度（单位mm）

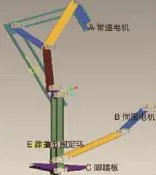
图3　辅助康复机构Pro/E建模图

图2脚踏板处运动轨迹

康复机构主要部件三维建模图如图3所示。A常速电机提供主要动力，带动腿部上下运动，辅助人体髋关节恢复运动机能；D滑块是结合常速电机与伺服电机两个驱动的枢纽；E踝关节固定环是固定腿部随着脚踏板一起运动；C脚踏板与摇杆是销钉连接，属于欠驱动的范畴，可以利用摇杆在水平面的摇摆让脚部有翘起运动，辅助踝关节恢复运动机能；B伺服电机驱动的曲柄连杆机构，可以使膝关节得以运动，辅助膝关节恢复运动机能。A常速电机提供主动力，B伺服电机提供辅助动力，驱动的两个曲柄相互配合，最后在脚踏板C处输出类椭圆形轨迹，符合人体正常行走轨迹。