破甲弹战斗部侵彻高速运动靶板的数值模拟
2016-09-13山西中北大学机电工程学院孙国庆张国伟乔磊
山西中北大学机电工程学院 孙国庆 张国伟 乔磊
破甲弹战斗部侵彻高速运动靶板的数值模拟
山西中北大学机电工程学院孙国庆张国伟乔磊
由于国内外有关破甲弹对运动体侵彻课题研究很少,可借鉴的资源有限。本文主要使用理论分析和数值模拟相结合的方法,利用有限元软件ANSYS/LS-DYNA对破甲弹战斗部侵彻运动靶板进行仿真,得出了入射角和运动体速度对侵彻射流影响的一般性规律,为今后实验研究打下基础。
破甲弹;运动靶板;有限元;数值模拟
引言
靶板运动速度对射流破甲威力的影响主要表现在靶板对射流的横向剪切力矩。相对于静止靶板,运动靶板的剪切力矩会使射流发生严重的弯曲、偏转、变形,导致射流的断裂和分散。随着靶板速度的增加,靶板剪切力矩的影响也逐渐增大,干扰影响也趋于明显,射流变形越剧烈,对其后续侵彻能力也将产生较大的影响[1]。运动靶板对射流的干扰影响还体现在对射流能量的无效消耗上。静止靶板的侵彻,射流只在轴向方向上侵彻消耗能量,形成笔直的侵彻孔;而运动靶板的侵彻,射流还要在靶板横向作用,浪费射流能量,扩大侵彻孔径,形成上粗下窄的倾斜的侵彻孔。随着靶板运动速度的增加,倾斜孔径越大,消耗射流能力越大[2]。
1 计算模型
将靶板速度取为 400m/s、600m/s、800m/s三种情况分别进行动态斜侵彻分析仿真计算。战斗部几何模型如图1所示。标靶板五种材料的破甲战斗部有限元模型,调整适宜的网格密度,设置恰当的边界约束(空气域无反射边界约束),使用正确的算法(ALE算法),确保计算结果准确。求解计算时的单位为cm-g-μs-Mbar。

图1 战斗部示意图建立药型罩、主装药、壳体、空气和目
考虑到靶板的运动情况特意将靶板偏离药型罩,以保证在整个侵彻过程中,射流尽可能地作用于靶板的中部,避免受到边界效应的影响,这也是建模时确定靶板尺寸的依据[3]。考虑到战斗部和目标靶板结构的轴对称性,简化模型为二分之一模型,主装药、药型罩和空气设置多物质ALE算法,采用Euler网格建模,靶板和壳体采用Lagrange网格建模,并且各材料之间使用耦合算法。
2 数值模拟
图2、图3、图4分别是靶板速度为v=400m/s,v=600m/s,v=800m/s时不同时刻射流侵彻过程图。

图2 v=400m/s时不同时刻射流侵彻过程
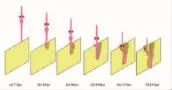
图3 v=600m/s时不同时刻射流侵彻过程

图4 v=800m/s时不同时刻射流侵彻过程
3 结果分析
运动靶板对射流侵彻体的影响,主要表现在其对射流侵彻体的横向扰动作用,使射流侵彻体弯曲和失稳,从而降低破甲能力。从图2中,我们可以很明显地看出射流侵彻过程中,由于受运动靶板的横向扰动干扰射流变形弯曲,并在侵彻孔内左右摆动。为了更细致地分析各射流段受横向干扰的影响,特将射流的侵彻过程分为三个阶段。在射流侵彻的初始阶段,即射流与靶板侧壁接触前,射流头部几乎没有弯曲变形,说明射流头部具有较高的速度,抗干扰能力相对较强,如图2中96μs以前;在射流开始出现弯曲变形阶段,即射流受到靶板的横向扰动开始弯曲,射流头部高速段和较高速段同时受到干扰变形弯曲,其产生的影响大小也因为射流段不同而不同,射流头部影响变形较小,射流中段影响变形较大,这说明速度越低对干扰越敏感,如图2中108μs左右;在射流侵彻震荡阶段,即射流在侵彻孔内碰撞,射流不断受到靶板的横向干扰弯曲变形更剧烈、更复杂,并在侵彻孔左右侧摆动,如图2中108μs以后。
运动靶板速度v=600m/s和v=800m/s时,对于同一种射流的侵彻过程,射流弯曲变形情况大致相同,如图3和图4所示。第一阶段,射流几乎没有变形;第二阶段,射流弯曲变形都发生在射流的中部低速段;第三阶段,射流震荡向下侵彻。从以上分析可以得出,运动靶板对射流的影响主要体现在对射流中部低速段的横向干扰,速度越低干扰越大,经过干扰后的射流作用于射流高速段头部,进而影响射流侵彻。
4 结论
与侵彻静止和相对静止靶板相比,射流侵彻运动靶板时的主要区别在于射流具有了一定的径向速度vjx。射流径向速度vjx的干扰作用主要体现在:其大小的变化和方向的无序性导致射流不同部位受到的干扰方向不同,加大了对射流的影响,最终导致射流容易弯曲甚至断裂。
[1]周权.聚能装药破甲侵彻深度与穿孔直径多目标优化设计研究[D].南京:南京理工大学,2007.
[2]隋树元,王树山.终点效应学[M].北京:国防工业出版社,2000:196-232.
[3]耿世才.小口径破甲弹的研究[D].南京理工大学硕士论文.2010:5-15.自适应问题,需要对管道机器人通过弯管的情况进行仿真分析。假定弯管机器人重心位置为几何中心,则对弯管设定路径配合,其重心会沿管道重心轴线运动,对管壁施加压力的方向上的偏航控制为10mm。最后,检查运动干涉,确定运动中无过定义和欠定义的情况发生。
3 运动学仿真分析
本部分针对弯管的曲率半径和通过速度对机器人弯管的通过性影响进行运动仿真。在管道机器人通过弯管时,弯管的曲率半径和机器人的通过速度对通过性和运动的稳定性有着重要影响。
由理论分析可知,曲率半径越大运动速度越快其通过性和稳定性越好。由于机器人在通过弯管时处于支撑装置内的压缩弹簧长度会受重力、离心力以及摩擦力等外界因素的影响。所以支撑轮上的压缩弹簧在通过弯管时的线性位移变化,会在一定程度上反映机器人通过弯管的平稳性[7]。
分别设定路径配合马达以50mm/s、100mm/s两种速度等速运动,通过曲率半径R为350mm的管道和以50mm/s、100mm/s两种速度等速运动,通过曲率半径R为500mm的管道,进行运动仿真分析,并将仿真结果通过MATLAB编制函数进行处理[8],最终处理结果如图3所示。
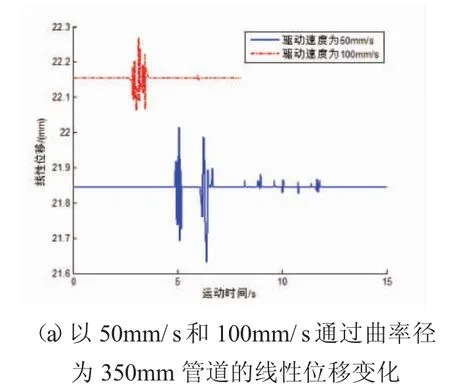
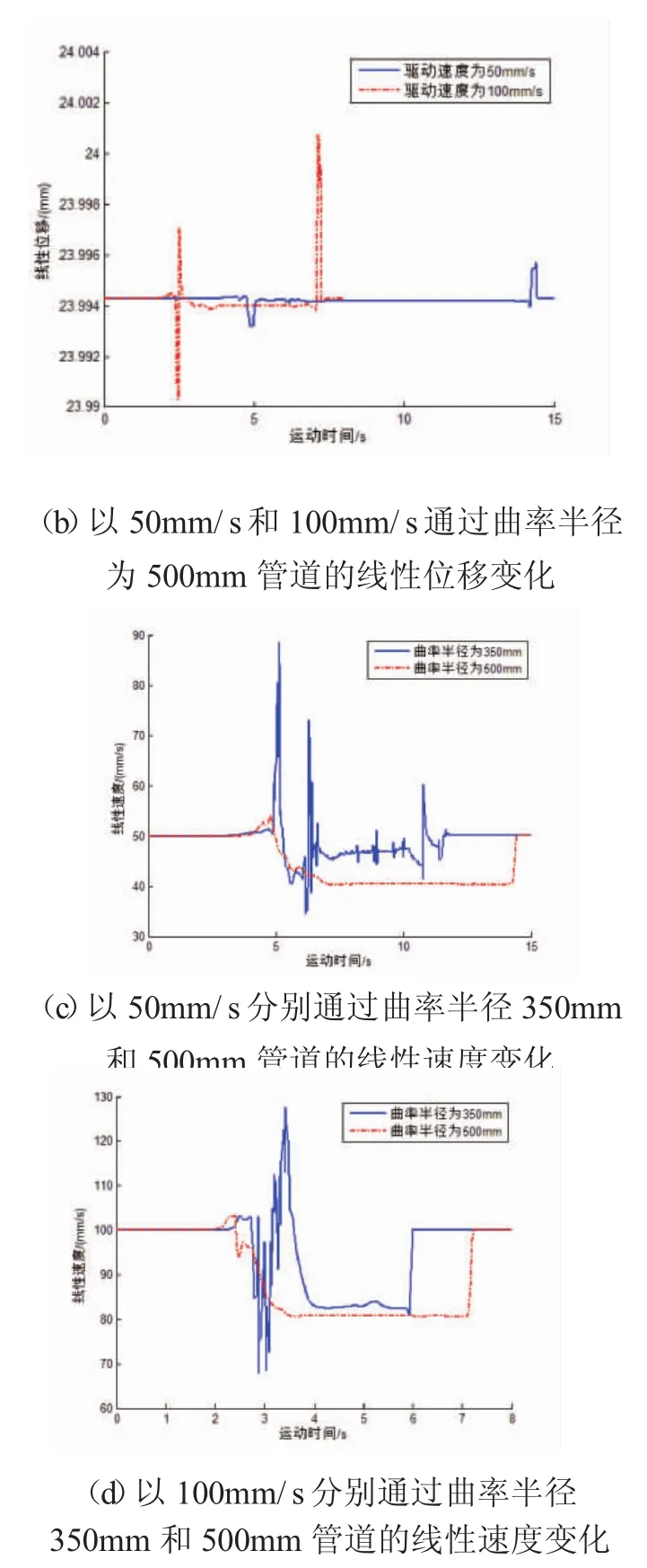
图3 弯管仿真示意图
对比图3(a)、(b)中的数据可以得出,在以较低速度通过弯管时,其线性位移幅值变化范围较小,运动平稳性较好,所受冲击载荷较为均匀。对比图3(c)、(d)可以得出,在以较大曲率半径通过弯管时,其支撑轮上的线性速度和线性加速度幅值变化较小,运动平稳性较好,所受冲击载荷较为均匀。
4 总结
通过本次仿真结果可以看出,支撑轮上的压缩弹簧的预紧状态对弯管机器人的运动平稳性和对弯管的通过性有着重要的影响。通过对弯管的运动仿真,验证了本次设计的管道机器人在较小曲率半径为350mm和较小驱动速度为50mm/s下具有良好的通过性和平稳性,能够更好地适应弯管中的运动。
本次设计的motion运动环境下弯管机器人虚拟样机模型为原理样机的结构设计提供了一定的理论依据,也为管道机器人的应用研究提供了数据支持。
参考文献:
[1]曹建树,林立,李杨,李魁龙.油气管道机器人技术研发进展 [J].油气储运,2013,32(1):1-7.
[2]焦圣喜,阚一凡,赵远新.基于Solid-Works的管道除垢机器人设计与实现[J].机床与液压,2014,42(3):65-67.
[3]李杨,曹建树,廖建泉,李魁龙.支撑轮式管道机器人牵引机构结构设计[J].北京石油化工学院学报,2013,21(1):29-32.
[4]卢海星,胡仁喜.Solidworks 2014有限元、虚拟样机与流场分析从入门到精通 [M].北京:机械工业出版社,2014:296-297.
[5]张晋西,郭学琴.Solidworks及COSMOSMotion机械仿真设计[M].北京:清华大学出版社,2007:10-11.
[6]孙丹,韩继光,王殿君,刘进福,张传艳.四轮管道机器人的通过性能研究[J].徐州师范大学学报(自然科学版),2011,29(4):71-74.
[7]李庆凯,唐德威,姜生元,邓宗全.管道机器人弯管运动转体原因分析[J].西安交通大学学报,2011,45(10):19-23+29.
[8]张志涌.精通MATLAB R2011a[M].北京:北京航空航天大学出版社,2011:9-13.
