超声波法检测木材内部孔洞缺陷的研究

2016-09-13程小武陆伟东刘伟庆

西南林业大学学报 2016年1期

关键词：传播速度木结构边界条件

张　甜　程小武　陆伟东　刘伟庆

(南京工业大学土木工程学院，江苏南京 211816)

超声波法检测木材内部孔洞缺陷的研究

张甜程小武陆伟东刘伟庆

(南京工业大学土木工程学院，江苏南京 211816)

利用Sylvatest-Duo超声波检测仪对健康杉木材和含有不同孔洞缺陷尺寸的杉木材进行测试，得到超声波传播速度与不同孔洞直径的定量关系。结果表明：超声波在杉木健康材中的径向传播速度范围为1 423 ～1 672m/s；杉木内部存在缺陷时，超声波径向传播速度会明显降低；通过对超声波传播速度与缺陷直径大小的回归，发现二者存在明显的负相关性，决定系数>0.8；采用指数函数模型和线性函数模型对缺陷大小与超声波传播速度进行回归分析，发现不同类型的缺陷理想回归模型不同。

木材；超声波；无损检测；Sylvatest-Duo；缺陷

我国历史文化悠久，现存有大量的古建筑，是国家的重要历史文化遗产，理应受到重点保护。我国的古建筑大多为木结构框架体系，这种体系被誉为世界三大建筑体系之一。

木材的缺陷能够影响木构件的外观及其力学性能，已经成为木材应用中存在的一个不能忽视的问题。木结构在长期的使用过程中，有害生物容易迅速侵入繁殖，使木材发生腐朽虫蛀，产生腐朽、孔洞、裂缝等缺陷，导致其物理力学性能降低，造成木结构的损毁[1-2]。因此，在木结构的日常维护工作中，对木构件材质状况进行检测以及安全性能分析非常重要。传统检测采用定性的目测法与简单的敲击法，检测结果不够准确。近年来，无损检测因其准确、客观等优点被广泛采用。超声波检测是当前木结构无损检测方法中最有效的检测手段之一，能够快速、准确地发现木材中存在的隐患及病害，快速对木材缺陷进行有效检测，判断活立木、原木、木结构存在的内部缺陷，预报其安全状况，为古建筑的安全评价提供可靠方法，对工程的安全运行有着极为重要的意义。

研究资料表明，应用超声波对木材缺陷进行检测已有50多年的历史，日本学者于1965年首先采用超声波方法，对气干木材的各种内部缺陷与波速之间的关系进行研究，之后美国，澳大利亚等国学者对不同树种的超声波检测也进行研究。McDonaldKA等[3]对木结构中存在的木节进行了检测；BütlerR等[4]对有腐朽缺陷的欧洲云杉(Picea asperata)原木的超声波传播速度进行测试，发现木材腐朽越严重，超声波传播速度越小；LinCJ等[5]利用超声波对原木的孔洞缺陷进行研究，分析超声波传播的不同路径与孔洞直径的关系；ReinprechtL等[6]从生物学的角度对木材的腐朽状况进行分析，同时对不同腐朽程度的超声波传播速度和动弹性模量的降低进行了研究；TallavoF等[7]对超声波检测时换能器的布置方法、发射波频率的变化等传播因素对超声波传播的影响进行了研究；NoyaJR等[8]将超声波无损检测方法应用于现场检测中，利用超声波法对现存的17世纪历史建筑进行了无损检测；而OhJ等[9]则根据超声波的衰减对建筑中木构件的缺陷进行检测；CondeMJM等[10]研究指出，利用超声波检测传统木结构，不仅可以将对传统建筑的破坏降到最低，同时根据检测结果可以有效节省修缮材料。国内学者自20世纪80年代开始进行了木材超声波检测的研究，李华等[11]应用超声波检测法对大钟寺博物馆某钟架结构进行检测，对其空洞、腐朽、裂缝等缺陷进行分析，为超声波应用于古建筑木构件的无损检测提供了科学依据；于文勇[12]利用超声波对木材内部孔洞缺陷进行了定量研究，根据超声波传播过程中波形图的变化对缺陷进行分析判断，再根据超声波首波幅值倒数的变化绘制的平面封闭图形，确定孔洞存在的位置及大小；宋世全等[13]分别利用超声波检测仪和阻抗仪对小叶杨(Populus simonii)活立木进行检测，通过对超声波在小叶杨立木健康材和缺陷材中径向传播速度的研究，对缺陷直径大小与超声波传播速度的关系进行了分析；王娜等[14-15]、高山等[16]、王立海等[17-18]基于小波分析理论和超声波传播场理论对应用超声波评估木材内部孔洞、腐朽缺陷进行了研究。

本试验在超声波检测的研究基础上，利用超声波分别对健康原木和含孔洞缺陷的原木进行测试，分析孔洞缺陷对超声波传播速度的影响，为准确评估木材内孔洞尺寸提供理论基础，也为古建筑中木构件检测和维修提供依据，使古建筑的保护工作更加科学化。

1　材料与方法

1.1试验材料

以我国南方古建筑中常用杉木(Cunninghamia lanceolata)为对象，原木取自安徽宣城，长4m，小头直径为15cm，大头直径为18cm。立木采伐后经扒皮、刨光、锯切，养护至含水率为19%以下。将试样加工成圆盘型，便于径向检测，圆盘直径为150～180mm。

1.2孔洞缺陷

人造孔洞缺陷为大孔洞(L)、小孔洞(S)2类，孔洞深度均为10cm，沿着原木径向方向。其中大孔洞试样厚度为10cm，孔洞位置在试样中心，其直径根据试样不同而改变；小孔洞试样厚度为40cm，其直径分别为1.4、2.0cm，沿直径方向排列不同数量的小孔洞。试样编号及孔洞直径、数量见表1。

表1　试样编号及孔洞直径与数量

1.3测试仪器及方法

超声波在木材中传播，如果遇到缺陷，会使超声波的正常传播发生变化。根据费马原理，超声波应该绕过缺陷进行传播，使传播时间变长，传播速度降低，同时超声波能量也会衰减。通过理论分析可知，超声波在木材中传播的边界条件是：当孔洞直径率(d/D)=0(d为孔洞直径，D为原木直径)时，超声波传播速度不会减小，接近于标准波速；当d/D=1时(假设超声波在空气中传播)，其传播速度为340m/s。

超声波检测仪采用瑞士生产的Sylvatest-Duo木材检测仪，频率22kHz，使用改良式锥形换能器置于试样两端进行测试。大孔洞试样测试时，每个试样绕圆形每隔120°检测1次，共3个方向每个方向测3次，取平均值。大孔洞试样标准波速值为无缺陷材中超声波的传播速度。

小孔洞试样测试时，每个试样沿缺陷厚度方向取3个点检测，每个点测3次，取平均值。小孔洞试样标准波速测试方法是：在每个试件健康区取3个点进行检测，每个点测3次，取平均值。

2　结果与分析

2.1径向超声波传播速度与大孔洞缺陷的关系

2.1.1径向超声波传播速度与孔洞直径率的关系

采用线性函数和指数函数对径向超声波传播速度与孔洞直径率的关系进行拟合，结果见图1。

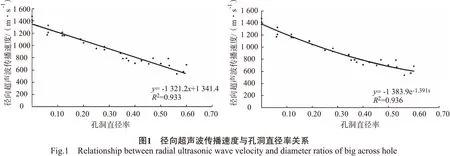
由图1可以看出，对比指数拟合方程和线性拟合方程，发现其决定系数相差不大。本试验中无孔洞缺陷的径向超声波平均传播速度为1 423m/s，其线性关系式、指数关系式及边界条件见表2。由表2可知，径向超声波传播速度与大孔洞直径的指数函数拟合更符合边界条件。

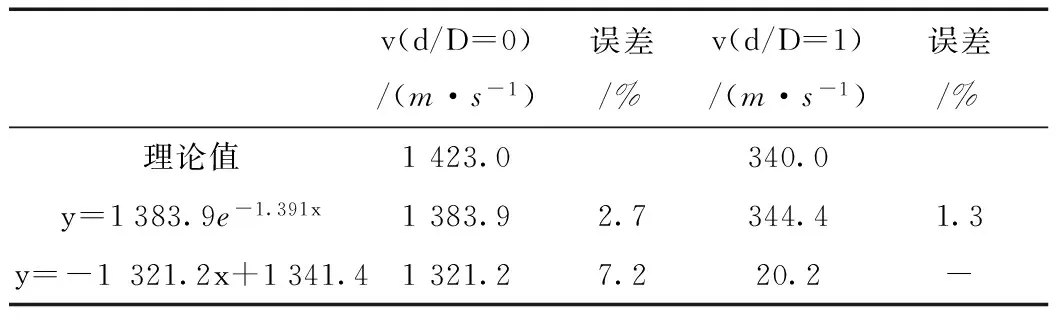
表2　径向超声波传播速度与大孔洞直径率的边界条件

2.1.2径向超声波传播速度与孔洞面积率的关系

采用线性函数和指数函数对径向超声波传播速度与孔洞面积率(d2/D2)的关系进行拟合，结果见图2。

由图2可以看出，对比指数拟合方程和线性拟合方程，发现指数拟合方程的决定系数大于线性拟合方程。本试验无孔洞缺陷的径向超声波平均传播速度为1 423m/s，线性关系式、指数关系式及边界条件见表3。由表3可知，径向超声波传播速度与孔洞面积率的指数函数拟合更符合边界条件。

通过径向超声波传播速度与孔洞直径率和面积率的指数关系式对比，得出径向超声波传播速度与孔洞直径率的相关性更大，且边界条件也更理想。

表3　径向超声波传播速度与大孔洞面积率的边界条件

v(d2/D2=0)/(m·s-1)误差/%v(d2/D2=1)/(m·s-1)误差/%理论值1423.0340.0y=1199.5e-2.197x1199.515.7133.3-y=-2021.5x+1197.51197.515.8-824.0-

2.2径向超声波传播速度与小孔洞缺陷的关系

2.2.1径向超声波传播速度与孔洞直径率的关系

采用线性函数和指数函数对径向超声波传播速度与孔洞直径率的关系进行拟合，结果见图3。

由图3可以看出，对比指数拟合方程和线性拟合方程，发现指数相关方程的决定系数大于线性相关方程。本试验测试无孔洞缺陷的径向超声波平均传播速度为1 672m/s，线性关系式、指数关系式及边界条件见表4。由表4可知，径向超声波传播速度与孔洞直径率的线性相关方程更符合边界条件，当孔洞数量越多，孔洞直径越大时，线性函数拟合表达更准确。

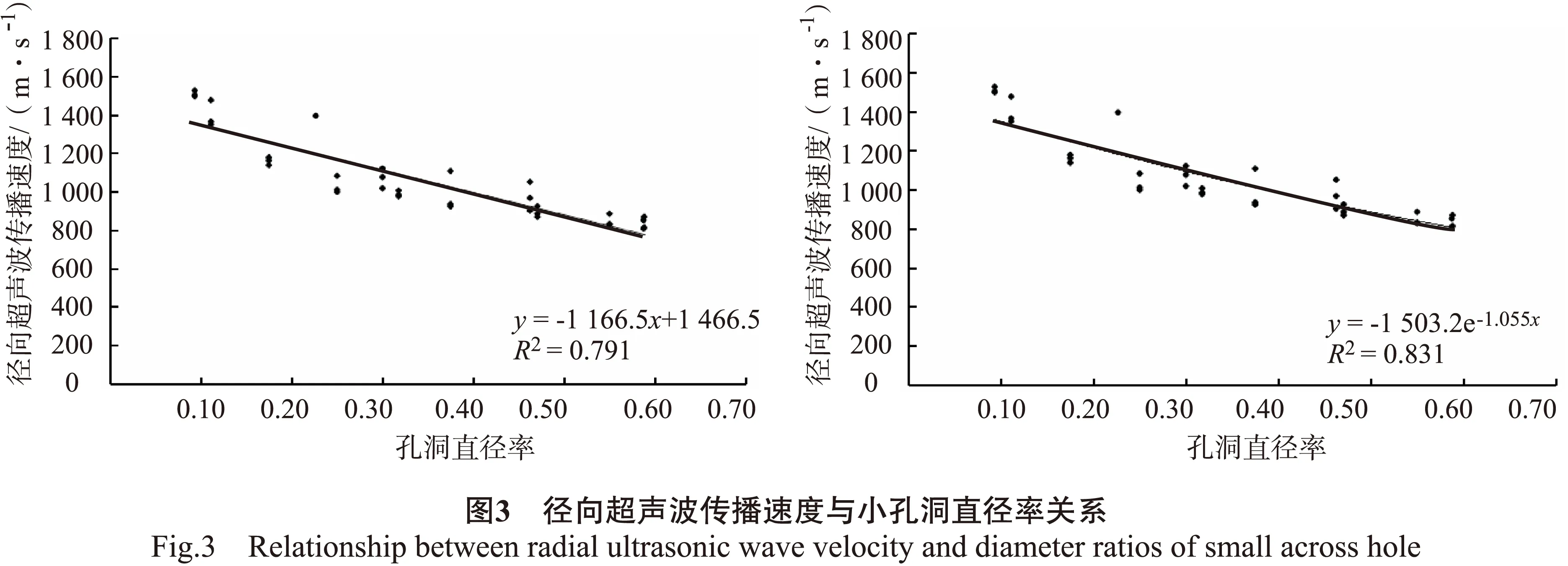
表4　径向超声波传播速度与小孔洞直径率的边界条件

v(d/D=0)/(m·s-1)误差/%v(d/D=1)/(m·s-1)误差/%理论值1627.0340.0-y=1503.2e-1.055x1503.27.6523.04.0y=-1166.5x+1466.51466.59.9300.011.8

2.2.2径向超声波传播速度与孔洞数量的关系通过试验发现，径向超声波传播速度随着孔洞数量的增加逐渐降低，以2cm孔洞缺陷为例进行分析，发现随着孔洞数量的增加，传播速度的下降速率逐渐减小，其速度降低率分别为16.3%，26.1%，9.8%，3.9%，1.6%(图4)。

2.3不同缺陷超声波传播速度对比

对上述2种缺陷的检测试验结果进行分析，发现超声波在大孔洞缺陷和小孔洞缺陷中传播的速度的变化率不同。

以10cm孔洞缺陷(图5)的径向传播速度下降率为例进行计算，当缺陷如图5a时，超声波速度平均下降率为59.57%，当缺陷如图5b时，超声波速度平均下降率为50.36%。超声波在大孔洞缺陷传播中的速度下降率与小孔洞缺陷传播中的结果相比，相差不大。因此，超声波在检测木材缺陷时对缺陷的宽度检验并不灵敏。

3　结论与讨论

1) 当超声波在杉木健康材中传播，径向传播速度为1 423～1 672m/s，当木材内部存在缺陷时，超声波传播速度均<1 423m/s。

2) 随着孔洞直径的增加，超声波径向传播速度逐渐降低；随着孔洞数量的增加，超声波径向传播速度也逐渐降低。对超声波传播速度与不同类型的孔洞直径进行回归，大孔洞直径与超声波传播速度的相关性大于小孔洞。

3) 将超声波传播速度与大孔洞直径率、面积率分别进行一元线性回归和指数回归，根据超声波传播速度的边界条件，得到超声波传播速度与大孔洞直径率的指数方程模型更理想，与大孔洞面积率的指数模型也优于线性模型，但其相关性小于前者且边界条件也不理想。

4) 将超声波传播速度与小孔洞直径率分别进行一元线性回归和指数回归，根据超声波传播速度的边界条件，得到超声波传播速度与小孔洞直径率的一次线性方程模型更理想，且随着孔洞数量的增加，超声波传播速度的下降率有逐渐减小的趋势。

5) 古建筑作为历史文物，一般不可拆卸，因此现场快速、准确勘测古建筑木构件内部缺陷的研究一直是相关研究人员关注和探索的问题之一。本文的径向超声波检测方法可以应用于今后的木结构现场初步检测，但是要确定缺陷存在的具体位置还应该结合微钻阻力仪或断层成像仪无损检测方法，准确判定缺陷的位置与尺寸。如何合理的结合无损检测方法，提高检测结果精度，增加实际可操作性，是古建筑木结构无损检测后续的研究重点。

[1] 陈允适, 刘秀英, 李华,等. 古建筑木结构的保护问题[C]// 中国紫禁城学会论文集(第五辑上).北京：2007:332-343.

[2]陈允适.古建筑木结构与木质文物保护[M].北京:中国建筑工业出版社，2007.

[3]McdonaldKA,CoxRG,BulgrinEH.LocatingLumberDefectsbyUltrasonics.[M].LocatingLumberDefectsbyUltrasonics, 1969.

[4]BütlerR,PattyL,BayonRCL,etal.LogdecayofPiceaabiesintheSwissJuramountainsofcentralEurope[J].ForestEcology&Management, 2007, 242:791-799.

[5]LinCJ,KaoYC,LinMJ.Applicationofanultrasonictomographictechniquefordetectingdefectsinstandingtrees[J].InternationalBiodeterioration&Biodegradation, 2008, 62(4):434-441.

[6]ReinprechtL,HibkyM.Thetypeanddegreeofdecayinsprucewoodanalyzedbytheultrasonicmethodinthreeanatomicaldirections[J].Bioresources, 2011, 6(4):4953-4968.[7]TallavoF,CascanteG,PandeyMD.Anovelmethodologyforconditionassessmentofwoodpolesusingultrasonictesting[J].Ndt&EInternational, 2012, 52(4):149-156.

[8]NoyaJR.Combinedmethodologyforultrasoundtestinginatimberstructureofthe17thcentury[C]//18thSymposiumNondestructiveTestingofWood.Madison， 2013：216-223.

[9]OhJ，EuS，LeeJ.Useofultrasonicattenuationtodetectinternalsmalldefectsformaintenanceofhistoricbuildings[C]//18thSymposiumNondestructiveTestingofWood.Madison， 2013：261-268.

[10]CondeMJM,Li09ánCR,HitaPRD.Useofultrasoundasanondestructiveevaluationtechniqueforsustainableinterventionsonwoodenstructures[J].Building&Environment, 2014, 82:247-257.

[11]李华, 刘秀英. 大钟寺博物馆钟架的超声波无损检测[J]. 木材工业, 2003, 17(2):33-36.

[12]于文勇.基于超声波原木内部孔洞缺陷定量检测[D].哈尔滨：东北林业大学，2006.

[13]宋世全, 徐华东, 王立海. 小叶杨立木横断面的超声波传播速度[J]. 东北林业大学学报, 2010, 38(5):40-43.

[14]王娜.基于超声波传播场的原木及板材空洞缺陷定量检测[D]. 哈尔滨：东北林业大学，2012.

[15]WangLH,WangN,XuHD.Effectofemissionpointsonultrasonictestingaccuracyofloginternaldecay[J].AdvancedMaterialsResearch, 2011, 337:682-685.

[16]WangL，GaoS，WangN，etal.Quantitativedetectionofvoiddefectsinlogsectionbasedonultrasonicwavespreadfield[C]//18thSymposiumNondestructiveTestingofWood.Madison， 2013：171-179.

[17]WangL,LiL,QiW,etal.Patternrecognitionandsizedeterminationofinternalwooddefectsbasedonwaveletneuralnetworks[J].Computers&ElectronicsinAgriculture, 2009, 69(2):142-148.

[18]WangN,WangLH,XuHD.Thepredictiononthesizeandlocationofinternaldefectsofstandingtreesusingultrasonictechnology[J].KeyEngineeringMaterials, 2011, 467-469:1838-1845.

(责任编辑曹龙)

Experimental Study on Testing Internal Hole Defects ofWoodbyUltrasonicMethod

Zhang Tian, Cheng Xiaowu, Lu Weidong, Liu Weiqing

(College of Civil Engineering，Nanjing Tech University，Nanjing Jiangsu 211816，China)

Onthebasisofultrasonicnondestructivetesting,usingSylvatest-Duoultrasonicdetectortotestthehealthywoodandinternaldifferentsizesdefectswood,achievedthequantitativerelationshipbetweenultrasonicpropagationvelocityandholediameters.Theanalysisresultsshowedthattheradialvelocityofultrasonicspreadinginthehealthywoodwasrangeof1 423 -1 627m/s2;thewoodinternalholedefectscouldcausethesignificantlydecreaseoftheradialvelocityofultrasonicspreading.Therelationshipbetweentheultrasonicpropagationvelocityandthesizeofthedefectdiameterswerefittedtocurves,anddefectsizewassignificantlynegativelycorrelatedwithradialvelocity,thehighfittingdegreeof>0.8.Exponentialfunctionmodelandalinearfunctionmodelwereadoptedtoanalyzetherelationshipbetweentheultrasonicpropagationvelocityandthesizeofthedefectdiameter，andfoundthattheidealmathematicalmodelofdifferenttypesdefectswasdifferent.

wood；ultrasonic；nondestructivetesting；Sylvatest-Duo；defects